Построение графика
работы сил сопротивления производится
путем графического интегрирования
графика приведенного момента сил
сопротивления.
Отрезок интегрирования
ОК выбираем равным 50 мм.
После построения графика суммарной
работы сил сопротивления определим
масштаб по следующей формуле:
График суммарной
работы
построим, сложив в каждом положении
ординаты работы движущих сил и сил
сопротивления.
Таблица 1.5
|
A(Mcyм |
Дж |
1489 |
2422 |
2644 |
2555 |
2111 |
655 |
-1722 |
-4778 |
-7222 |
-9178 |
-10600 |
-10644 |
|
А(Мдв) |
Дж |
855 |
1733 |
2633 |
3489 |
4367 |
5255 |
6111 |
7000 |
7889 |
8778 |
9644 |
10644 |
|
Асум |
Дж |
2344 |
4155 |
5277 |
6044 |
6478 |
5910 |
4389 |
2222 |
667 |
-400 |
-956 |
0 |
1.6 Определение работы движущих сил и момента движущих сил
При установившемся
движении суммарная работа за цикл
,
следовательно, работа движущих сил за
цикл по величине равна работе сил
сопротивления:
.
Конечная ордината графика
должна быть равна нулю: это признак
установившегося движения. Из этого
условия, считая момент движущих сил
постоянным , определим сначала работу,
а затем обратным интегрированием
приведенный момент движущих сил.
1.7 Определение приведённых моментов инерции звеньев.
Приведение моментов
инерции осуществили на основе метода
приведения масс.Для определения
приведённого момента инерции каждого
звена механизма составили равенство
кинетических
энергий рассматриваемого звена и звена
модели.
Поршни 3 и 5 совершают
поступательное движение:
.
Шатуны 2 и 4 совершают
плоскопараллельное движение:
.
После алгебраических
преобразований получили:
,
Для
первого звена: Iпр1=const.
Результаты расчетов
приведены в таблице 2.
Масштаб графиков
График суммарного
приведенного момента инерции второй
группы звеньев получаем как графическую
сумму всех составляющих.
Суммарный приведённый
момент инерции нашли по формуле:
Где IпрI,-
приведённый момент инерции первой
группы звеньев,
IпрII—
приведённый момент инерции второй
группы звеньев.
Таблица 1.7
|
I |
кг*м^2 |
0,009 |
0,003 |
0 |
0,003 |
0,009 |
0,011 |
0,009 |
0,003 |
0 |
0,003 |
0,009 |
0,011 |
|
I |
кг*м^2 |
0,371 |
0,549 |
0,631 |
0,474 |
0,324 |
0,28 |
0,324 |
0,474 |
0,631 |
0,549 |
0,371 |
0,28 |
|
I |
кг*м^2 |
0,38 |
0,553 |
0,631 |
0,477 |
0,333 |
0,292 |
0,333 |
0,477 |
0,631 |
0,553 |
0,380 |
0,292 |
|
I |
кг*м^2 |
0,133 |
0,305 |
0,315 |
0,15 |
0,033 |
0 |
0,033 |
0,15 |
0,315 |
0,305 |
0,133 |
0 |
|
I |
кг*м^2 |
0,003 |
0,009 |
0,011 |
0,009 |
0,003 |
0 |
0,003 |
0,009 |
0,011 |
0,009 |
0,003 |
0 |
|
I |
кг*м^2 |
0,246 |
0,169 |
0,140 |
0,169 |
0,246 |
0,315 |
0,305 |
0,202 |
0,14 |
0,202 |
0,305 |
0,315 |
|
I |
кг*м^2 |
0,249 |
0,178 |
0,152 |
0,178 |
0,249 |
0,315 |
0,308 |
0,211 |
0,152 |
0,211 |
0,308 |
0,315 |
|
I |
кг*м^2 |
0,162 |
0,035 |
0 |
0,035 |
0,162 |
0,315 |
0,305 |
0,143 |
0 |
0,143 |
0,305 |
0,315 |
|
I |
кг*м^2 |
1,805 |
2,055 |
2,132 |
1,748 |
1,611 |
1,781 |
1,87233 |
1,921 |
2,132 |
2,228 |
2,066 |
1,781 |
Соседние файлы в папке 136-й курсач
- #
- #
04.03.201482 Кб31Лист 4.cdw
- #
04.03.2014189.96 Кб29Лист1.bak
- #
04.03.2014190.15 Кб30Лист1.cdw
- #
04.03.201430.72 Кб31Лист1.xls
- #
04.03.201496.65 Кб30Лист2.cdw
Совершённая работа равна изменению энергии, потраченной на совершение работы.
Величину работы можно определить, вычитая из конечного значения энергии начальное значение энергии.
, где A — работа (Дж); E — энергия (Дж).
Работу, как и энергию, измеряют в джоулях (Дж).
Если энергия тела увеличивается, тогда общая совершённая работа является положительной.
Пример:
Когда автомобиль начинает двигаться, его кинетическая энергия увеличивается. Значит, двигатель автомобиля совершает положительную работу.
Если энергия тела уменьшается, тогда общая совершённая работа является отрицательной.
Пример:
Когда автомобиль свободно катится по горизонтальной поверхности, его скорость и кинетическая энергия уменьшаются. Значит, сила сопротивления совершает отрицательную работу.
В физике рассматривают физическую работу, которая связана с перемещением тел.
Если при прямолинейном движении на тело действует неизменная сила, направленная в сторону движения тела, тогда работа, произведённая приложенной силой, равна произведению величины силы на величину проделанного перемещения.
Если к телу приложена сила под вертикальным углом к направлению движения тела, как это показано на рисунке, тогда величина совершённой работы зависит от:
1) величины приложенной силы (F), которая совершает работу;
2) расстояния (l), на которое перемещается тело;
3) угла (α) между направлением действия силы и направлением движения тела.
Работа определяется по формуле: A=F⋅l⋅cosα.
Рис. (1). Под углом
Обрати внимание!
Если сила направлена параллельно направлению перемещения, тогда угол (α = 0), а (косинус) угла (α) равен (1). В этом случае формула упрощается:
A=F⋅l
.
Если проделанный путь является прямолинейным, тогда вместо пути (l) можно использовать перемещение (s).
В этом случае формула для расчёта работы приобретает такой вид:
A=F⋅s
.
На трёх рисунках изображены случаи, когда направление силы и направление движения тела совпадают.
1) Действие силы и направление движения тела направлены горизонтально. Например, автомобиль едет по прямому пути, и сила тяги автомобиля приложена в том же направлении.
Рис. (2). Параллельно
2) Действие силы и направление движения тела направлены под одинаковым углом наклона по отношению к горизонту. Например, автомобиль едет в гору.
Рис.(3). Движение «в гору»
3) Действие силы и направление движения тела направлены вертикально. Например, груз поднимается вверх, и сила упругости троса тоже направлена вверх. В этом случае величину совершённой работы можно рассчитать также по формуле
A=m⋅g⋅h
, где
(m) — масса тела, (g) — ускорение свободного падения,
(h) — высота подъёма тела над поверхностью земли.
Рис. (4). Движение вверх
Обрати внимание!
Если направление действия силы противоположно направлению движения, тогда совершаемая этой силой работа отрицательна.
Работа отрицательна, так как функция (косинус) в интервале значений угла (90° — 180°) является отрицательной.
Таким образом, любая работа, совершённая силой трения или сопротивления, является отрицательной.
Пример:
Когда автомобиль едет с равномерной скоростью по прямой дороге, как это показано на рисунке, работа силы тяги автомобиля является положительной, а работа силы сопротивления равна по величине, но является отрицательной. В результате этого кинетическая и потенциальная энергия автомобиля остаются неизменными.
Если сила направлена прямо противоположно направлению движения, тогда работу вычисляют по формуле:
A=−F⋅l
.
Рис. (5). Автомобиль
Источники:
Рис. 1. Под углом. © ЯКласс.
Рис. 2. Параллельно. © ЯКласс.
Рис. 3. Движение «в гору». © ЯКласс.
Рис. 4. Движение вверх. © ЯКласс.
Рис. 5. Автомобиль. © ЯКласс.
Решение.
Для
решения задачи рассмотрим физическую систему «тело – гравитационное поле Земли».
Тело будем считать материальной точкой, а гравитационное поле Земли — однородным. Выделенная физическая система
является незамкнутой, т.к. во время движения тела взаимодействует с воздухом.
Если не учитывать выталкивающую силу, действующую на тело со стороны воздуха,
то изменение полной механической энергии системы равняется работе силы
сопротивления воздуха, т.е.
∆
E
=
A c
.
Нулевой
уровень потенциальной энергии выберем на поверхности Земли. Единственной
внешней силой в отношении системы «тело – Земля» является сила сопротивления
воздуха, направленная вертикально вверх. Начальная энергия системы
E 1
, конечная
E 2
.
Работа
силы сопротивления
A.
Т.к.
угол между силой сопротивления и перемещением равен 180° , то косинус равен -1,
поэтому
A
= —
F c h
. Приравняем
A.
Рассматриваемую
незамкнутую физическую систему можно также описать теоремой от изменении
кинетической энергии системы взаимодействующих между собой объектов, согласно
которой изменение кинетической энергии системы равно работе, совершенной
внешними и внутренними силами при ее переходе из начального состояния в
конечное. Если не учитывать выталкивающую силу, действующую на тело со стороны
воздуха, а внутренней – сила тяжести. Следовательно
∆
E
к
=
A
1
+
A
2
, где
A
1
=
mgh
– работа силы тяжести,
A
2
=
F c hcos
180°
= —
F c h
– работа силы сопротивления;
∆
E
=
E
2
–
E
1
.
Это творческое задание для мастер-класса по информатике для школьников при ДВФУ.
Цель задания — выяснить, как изменится траектория тела, если учитывать сопротивление воздуха. Также необходимо ответить на вопрос, будет ли дальность полёта по-прежнему достигать максимального значения при угле бросания в 45°, если учитывать сопротивление воздуха.
В разделе «Аналитическое исследование» изложена теория. Этот раздел можно пропустить, но он должен быть, в основном, понятным для вас, потому что бо
льшую часть из этого вы проходили в школе.
В разделе «Численное исследование» содержится описание алгоритма, который необходимо реализовать на компьютере. Алгоритм простой и краткий, поэтому все должны справиться.
Аналитическое исследование
Введём прямоугольную систему координат так, как показано на рисунке. В начальный момент времени тело массой m
находится в начале координат. Вектор ускорения свободного падения направлен вертикально вниз и имеет координаты (0, —g
).
— вектор начальной скорости. Разложим этот вектор по базису: 
. Здесь , где
— модуль вектора скорости, — угол бросания.
Запишем второй закон Ньютона: .
Ускорение в каждый момент времени есть (мгновенная) скорость изменения скорости, то есть производная от скорости по времени: .
Следовательно, 2-й закон Ньютона можно переписать в следующем виде:
, где — это равнодействующая всех сил, действующая на тело.
Так как на тело действуют сила тяжести и сила сопротивления воздуха, то 
.
Мы будем рассматривать три случая:
1) Сила сопротивления воздуха равна 0:
.
2) Сила сопротивления воздуха противоположно направлена с вектором скорости, и её величина пропорциональна скорости: 
.
3) Сила сопротивления воздуха противоположно направлена с вектором скорости, и её величина пропорциональна квадрату скорости: 
.
Проанализируем полученные формулы.
Найдём время полёта
тела. Приравняв y
к нулю, получим
Дальность полёта
равна значению координаты x
в момент времени t
0:
Из этой формулы следует, что максимальная дальность полёта достигается при .
Теперь найдём уравнение трактории тела
. Для этого выразим t
через x
И подставим полученное выражение для t
в равенство для y
.
Полученная функция y
(x
) — квадратичная функция, её графиком является парабола, ветви которой направлены вниз.
Про движение тела, брошенного под углом к горизонту (без учёта сопротивления воздуха), рассказывается в этом видеоролике.
Теперь рассмотрим второй случай: .
Второй закон приобретает вид 
,
отсюда 
.
Запишем это равенство в скалярном виде:
Мы получили два линейных дифференциальных уравнения
.
Первое уравнение имеет решение
В чём можно убедиться, подставив данную функцию в уравнение для v x
и в начальное условие 
.
Здесь e = 2,718281828459… — число Эйлера .
Второе уравнение имеет решение
Так как 
,
, то при наличии сопротивления воздуха движение тела стремится к равномерному, в отличие от случая 1, когда скорость неограниченно увеличивается.
В следующем видеоролике говорится, что парашютист сначала движется ускоренно, а потом начинает двигаться равномерно (даже до раскрытия парашюта).
Найдём выражения для x
и y
.
Так как x
(0) = 0, y
(0) = 0, то
Нам осталось рассмотреть случай 3, когда .
Второй закон Ньютона имеет вид
, или
.
В скалярном виде это уравнение имеет вид:
Это система нелинейных дифференциальных уравнений
. Данную систему не удаётся решить в явном виде, поэтому необходимо применять численное моделирование.
Численное исследование
В предыдущем разделе мы увидели, что в первых двух случаях закон движения тела можно получить в явном виде. Однако в третьем случае необходимо решать задачу численно. При помощи численных методов мы получим лишь приближённое решение, но нас вполне устроит и небольшая точность. (Число π или квадратный корень из 2, кстати, нельзя записать абсолютно точно, поэтому при расчётах берут какое-то конечное число цифр, и этого вполне хватает.)
Будем рассматривать второй случай, когда сила сопротивления воздуха определяется формулой. Отметим, что при k
= 0 получаем первый случай.
Скорость тела 
подчиняется следующим уравнениям:
В левых частях этих уравнений записаны компоненты ускорения 
.
Напомним, что ускорение есть (мгновенная) скорость изменения скорости, то есть производная от скорости по времени.
В правых частях уравнений записаны компоненты скорости. Таким образом, данные уравнения показывают, как скорость изменения скорости связана со скоростью.
Попробуем найти решения этих уравнений при помощи численных методов. Для этого введём на временной оси сетку
: выберем число
и будем рассматривать моменты времени вида :
.
Наша задача — приближённо вычислить значения
в узлах сетки.
Заменим в уравнениях ускорение (мгновенную скорость
изменения скорости) на среднюю скорость
изменения скорости, рассматривая движение тела на промежутке времени :
Теперь подставим полученные аппроксимации в наши уравнения.
Полученные формулы позволяют нам вычислить значения функций в следующем узле сетки, если известны значения этих функций в предыдущем узле сетки.
При помощи описанного метода мы можем получить таблицу приближённых значений компонент скорости.
Как найти закон движения тела, т.е. таблицу приближённых значений координат x
(t
), y
(t
)? Аналогично!
Имеем
Значение vx[j] равняется значению функции , для других массивов аналогично.
Теперь остаётся написать цикл, внутри которого мы будем вычислять vx через уже вычисленное значение vx[j], и с остальными массивами то же самое. Цикл будет по j
от 1 до N
.
Не забудьте инициализировать начальные значения vx, vy, x, y по формулам , x
0 = 0, y
0 = 0.
В Паскале и Си для вычисления синуса и косинуса имеются функции sin(x)
, cos(x)
. Обратите внимание, что эти функции принимают аргумент в радианах.
Вам необходимо построить график движения тела при k
= 0 и k
> 0 и сравнить полученные графики. Графики можно построить в Excel.
Отметим, что расчётные формулы настолько просты, что для вычислений можно использовать один только Excel и даже не использовать язык программирования.
Однако в дальнейшем вам нужно будет решить задачу в CATS, в которой нужно вычислить время и дальность полёта тела, где без языка программирования не обойтись.
Обратите внимание, что вы можете протестировать
вашу программу и проверить ваши графики, сравнив результаты вычислений при k
= 0 с точными формулами, приведёнными в разделе «Аналитическое исследование».
Поэкспериментируйте со своей программой. Убедитесь в том, что при отсутствии сопротивления воздуха (k
= 0) максимальная дальность полёта при фиксированной начальной скорости достигается при угле в 45°.
А с учётом сопротивления воздуха? При каком угле достигается максимальная дальность полёта?
На рисунке представлены траектории тела при v
0 = 10 м/с, α = 45°, g
= 9,8 м/с 2 , m
= 1 кг, k
= 0 и 1, полученные при помощи численного моделирования при Δt
= 0,01.
Вы можете ознакомиться с замечательной работой 10-классников из г. Троицка, представленной на конференции «Старт в науку» в 2011 г. Работа посвящена моделированию движения теннисного шарика, брошенного под углом к горизонту (с учетом сопротивления воздуха). Применяется как численное моделирование, так и натурный эксперимент.
Таким образом, данное творческое задание позволяет познакомиться с методами математического и численного моделирования, которые активно используются на практике, но мало изучаются в школе. К примеру, данные методы использовались при реализации атомного и космического проектов в СССР в середине XX века.
Все составляющие
сопротивления воздуха трудно определяются
аналитически. Поэтому в практике нашла
применение эмпирическая формула, имеющая
для диапазона скоростей движения,
характерного для реального автомобиля,
следующий вид:
где с
х
– безразмерный
коэффициент
обтекаемости воздухом
,
зависящий от формы тела; ρ в
– плотность воздуха ρ в =
1,202…1,225 кг/м 3 ;
А
– площадь миделева сечения (площадь
поперечной проекции) автомобиля, м 2 ;
V
– скорость автомобиля, м/с.
В литературе
встречается коэффициент
сопротивления воздуха
k
в
:
F
в
=
k
в
А
V
2
,
где k
в
=с
х
ρ
в
/2
,
–коэффициент сопротивления воздуха,
Нс 2 /м 4 .
…и фактор
обтекаемости
q
в
:
q
в
=
k
в
· А.
Если вместо с
х
подставить с
z
,
то получим аэродинамическую подъемную
силу.
Площадь миделева
сечения для авто:
А=0,9 · В
max
· Н
,
где В
max
– наибольшая колея автомобиля, м; Н
– высота автомобиля, м.
Сила приложена в
метацентре, при этом создаются моменты.
Скорость сопротивления
потока воздуха с учетом ветра:
,
где β
– угол между направлениями движения
автомобиля и ветра.
С
х
некоторых автомобилей
|
ВАЗ 2101…07 |
Оpel |
|||
|
ВАЗ 2108…15 |
||||
|
Land |
||||
|
ВАЗ 2102…04 |
||||
|
ВАЗ 2121…214 |
||||
|
грузовик |
||||
|
грузовик с |
-
Сила сопротивления подъему
F
п
=
G
а
sin
α.
В дорожной практике
величину уклона обычно оценивают
величиной подъема полотна дороги,
отнесенную к величине горизонтальной
проекции дороги, т.е. тангенсом угла, и
обозначают i
, выражая полученное значение в процентах.
При относительно небольшой величине
уклона допустимо в расчетных формулах
при определении силы сопротивления
подъему использовать не sin
α., а величину i
в относительных
значениях. При больших значениях
величины уклона замена sin
α величиной тангенса (i
/100)
недопустима.
-
Сила сопротивления разгону
При разгоне
автомобиля происходит разгон поступательно
движущейся массы авто и разгон вращающихся
масс, увеличивающих сопротивление
разгону. Это увеличение можно учесть в
расчетах, если считать, что массы
автомобиля движутся поступательно, но
использовать некую эквивалентную массу
m
э,
несколько большей m
a
(в классической
механике это выражается уравнением
Кенига)
Используем метод
Н.Е. Жуковского, приравняв кинетическую
энергии поступательно движущейся
эквивалентной массы сумме энергий:
,
где J
д
– момент инерции маховика двигателя и
связанных с ним деталей, Н·с 2 ·м
(кг·м 2);
ω д
– угловая скорость двигателя, рад/с; J
к
–момент инерции одного колеса.
Так как ω к
= V
а
/
r
k
,
ω д
= V
а
·
i
кп
·
i
o
/
r
k
,
r
k
=
r
k
0
,
то получим
.
Момент инерции
J
узлов трансмиссии автомобилей, кг· м
2
|
Автомобиль |
Маховик |
Ведомые колеса (2 колеса с |
Ведущие колеса (2 колеса с |
Произведем замену:
m
э
=
m
а
·
δ,
Если автомобиль
загружен не полностью:
.
Если автомобиль
идет накатом: δ
= 1 + δ 2
Сила сопротивления
разгону автомобиля (инерции): F
и
=
m
э
· а
а
=
δ
·
m
а
· а
а
.
В первом приближении
можно принять: δ
= 1,04+0,04
i
кп
2
Дорожная эксплуатационная мощность, затрачиваемая на преодоление сопротивлений, весьма велика (см. рис.). Например, для поддержания равномерного движения (190 км/ч
) четырех дверного седана, массой 1670 кг
, площадью миделя 2,05 м 2
, С х = 0,45 требуется около 120 кВт
мощности, причем 75 % мощности затрачивается на аэродинамическое сопротивление. Мощности, затрачиваемые на преодоление аэродинамического и дорожного (качения) сопротивления приблизительно равны на скорости 90 км/ч, и в сумме составляют 20 – 25 кВт
.
Примечание к рисунку
: сплошная линия – аэродинамическое сопротивление; пунктирная линия – сопротивление качению.
Сила сопротивления воздуха Р w
обусловлена трением в прилегающих к поверхности автомобиля слоях воздуха, сжатием воздуха движущейся машиной, разрежением за машиной и вихреобразованием в окружающих автомобиль слоях воздуха. На величину аэродинамического сопротивления автомобиля влияет ряд и других факторов, главным из которых является его форма. В качестве упрощенного примера влияния формы автомобиля на его аэродинамическое сопротивление проиллюстрировано на схеме, приведенной ниже.
Направление движения автомобиля
Значительная часть всей силы сопротивления воздуха составляет лобовое сопротивление, которое зависит от лобовой площади (наибольшей площади поперечного сечения автомобиля).
Для определения силы сопротивления воздуха используют зависимость:
Р w
= 0,5·с х ·ρ·F·v n
,
где с х
– коэффициент, характеризующий форму тела и аэродинамическое качество машины (коэффициент аэродинамического сопротивления
);
F
— лобовая площадь автомобиля (площадь проекции на плоскость, перпендикулярную продольной оси), м 2
;
v
— скорость движения машины, м/с
;
n
— показатель степени (для реальных скоростей движения автомобилей принимается равным 2).
ρ
— плотность воздуха:
, кг/м 3
,
где ρ 0
= 1,189 кг/м
3 , р 0
= 0,1 МПа
, Т 0
= 293К
– плотность, давление и температура воздуха при нормальных условиях;
ρ
, р
, Т
– плотность, давление и температура воздуха при расчетных условиях.
При расчетах лобовую площадь F
легковых автомобилей со стандартным кузовом определяют по приближенной формуле:
F
= 0,8В г Н г
,
где В г
— габаритная ширина автомобиля, м
;
Н г
— габаритная высота автомобиля, м
.
Для автобусов и грузовых автомобилей с кузовом в виде фургона или с тентом:
F
= 0,9В Г Н Г
.
Для условий работы автомобиля плотность воздуха изменяется мало (ρ
= 1,24…1,26 кг/м 3
). Заменив произведение (0,5·с х ·ρ
) , через к w
, получим:
Р w
= к w ·F·v 2
,
где к w
– коэффициент обтекаемости
; по определению он представляет собой удельную силу в Н
, необходимую для движения со скоростью 1 м/с
в воздушной среде тела данной формы с лобовой площадью 1 м
2:
, Н·с 2 /м 4
.
Произведение (к w ·F
)называют фактором сопротивления воздушной среды
или фактором обтекаемости
, характеризующим размеры и форму автомобиля в отношении свойств обтекаемости (его аэродинамические качества).
Средние значения коэффициентов с х
, k w
и лобовых площадей F
для различных типов автомобилей приведены в табл. 2.1.
Таблица 2.1.
Параметры, характеризующие аэродинамические качества автомобилей
:
Известные значения аэродинамических коэффициентов c x
и k w
и площади габаритного поперечного (миделевого) сечения F
для некоторых серийно выпускаемых автомобилей (по данным заводов-изготовителей) приведены в табл. 2.1.-а
.
Таблица 2.1-а.
Аэродинамические коэффициенты и лобовая площадь автомобилей:
| № | Автомобиль | с х |
к w |
F |
| ВАЗ-2121 | 0,56 | 0,35 | 1,8 | |
| ВАЗ-2110 | 0,334 | 0,208 | 2,04 | |
| М-2141 | 0,38 | 0,24 | 1,89 | |
| ГАЗ-2410 | 0,34 | 0,3 | 2,28 | |
| ГАЗ-3105 | 0,32 | 0,22 | 2,1 | |
| ГАЗ-3110 | 0,56 | 0,348 | 2,28 | |
| ГАЗ-3111 | 0,453 | 0,282 | 2,3 | |
| «Ока» | 0,409 | 0,255 | 1,69 | |
| УАЗ-3160 (jeep) | 0,527 | 0,328 | 3,31 | |
| ГАЗ-3302 бортовой | 0,59 | 0,37 | 3,6 | |
| ГАЗ-3302 фургон | 0,54 | 0,34 | 5,0 | |
| ЗИЛ-130 бортовой | 0,87 | 0,54 | 5,05 | |
| КамАЗ-5320 бортовой | 0,728 | 0,453 | 6,0 | |
| КамАЗ-5320 тентовый | 0,68 | 0,43 | 7,6 | |
| МАЗ-500А тентовый | 0,72 | 0,45 | 8,5 | |
| МАЗ-5336 тентовый | 0,79 | 0,52 | 8,3 | |
| ЗИЛ-4331 тентовый | 0,66 | 0,41 | 7,5 | |
| ЗИЛ-5301 | 0,642 | 0,34 | 5,8 | |
| Урал-4320 (military) | 0,836 | 0,52 | 5,6 | |
| КрАЗ (military) | 0,551 | 0,343 | 8,5 | |
| ЛиАЗ bus (city) | 0,816 | 0,508 | 7,3 | |
| ПАЗ-3205 bus (city) | 0,70 | 0,436 | 6,8 | |
| Ikarus bus (city) | 0,794 | 0,494 | 7,5 | |
| Mercedes-Е | 0,322 | 0,2 | 2,28 | |
| Mercedes-А (kombi) | 0,332 | 0,206 | 2,31 | |
| Mercedes -ML (jeep) | 0,438 | 0,27 | 2,77 | |
| Audi A-2 | 0,313 | 0,195 | 2,21 | |
| Audi A-3 | 0,329 | 0,205 | 2,12 | |
| Audi S 3 | 0,336 | 0,209 | 2,12 | |
| Audi A-4 | 0,319 | 0,199 | 2,1 | |
| BMW 525i | 0,289 | 0,18 | 2,1 | |
| BMW- 3 | 0,293 | 0,182 | 2,19 | |
| Citroen X sara | 0,332 | 0,207 | 2,02 | |
| DAF 95 trailer | 0,626 | 0,39 | 8,5 | |
| Ferrari 360 | 0,364 | 0,227 | 1,99 | |
| Ferrari 550 | 0,313 | 0,195 | 2,11 | |
| Fiat Punto 60 | 0,341 | 0,21 | 2,09 | |
| Ford Escort | 0,362 | 0,225 | 2,11 | |
| Ford Mondeo | 0,352 | 0,219 | 2,66 | |
| Honda Civic | 0,355 | 0,221 | 2,16 | |
| Jaguar S | 0,385 | 0,24 | 2,24 | |
| Jaguar XK | 0,418 | 0,26 | 2,01 | |
| Jeep Cherokes | 0,475 | 0,296 | 2,48 | |
| McLaren F1 Sport | 0,319 | 0,198 | 1,80 | |
| Mazda 626 | 0,322 | 0,20 | 2,08 | |
| Mitsubishi Colt | 0,337 | 0,21 | 2,02 | |
| Mitsubishi Space Star | 0,341 | 0,212 | 2,28 | |
| Nissan Almera | 0,38 | 0,236 | 1,99 | |
| Nissan Maxima | 0,351 | 0,218 | 2,18 | |
| Opel Astra | 0,34 | 0,21 | 2,06 | |
| Peugeot 206 | 0,339 | 0,21 | 2,01 | |
| Peugeot 307 | 0,326 | 0,203 | 2,22 | |
| Peugeot 607 | 0,311 | 0,19 | 2,28 | |
| Porsche 911 | 0,332 | 0,206 | 1,95 | |
| Renault Clio | 0,349 | 0,217 | 1,98 | |
| Renault Laguna | 0,318 | 0,198 | 2,14 | |
| Skoda Felicia | 0,339 | 0,21 | 2,1 | |
| Subaru Impreza | 0,371 | 0,23 | 2,12 | |
| Suzuki Alto | 0,384 | 0,239 | 1,8 | |
| Toyota Corolla | 0,327 | 0,20 | 2,08 | |
| Toyota Avensis | 0,327 | 0,203 | 2,08 | |
| VW Lupo | 0,316 | 0,197 | 2,02 | |
| VW Beetl | 0,387 | 0,24 | 2,2 | |
| VW Bora | 0,328 | 0,204 | 2,14 | |
| Volvo S 40 | 0,348 | 0,217 | 2,06 | |
| Volvo S 60 | 0,321 | 0,20 | 2,19 | |
| Volvo S 80 | 0,325 | 0,203 | 2,26 | |
| Volvo B12 bus (tourist) | 0,493 | 0,307 | 8,2 | |
| MAN FRH422 bus (city) | 0,511 | 0,318 | 8,0 | |
| Mercedes 0404(inter city) | 0,50 | 0,311 | 10,0 |
Примечание:
c x
, Н·с 2 /м·кг; к w
, Н·с 2 /м 4
– аэродинамические коэффициенты;
F
, м 2
– лобовая площадь автомобиля.
Для автомобилей, имеющих высокие скорости движения, сила Р w
имеет доминирующее значение. Сопротивление воздушной среды определяется относительной скоростью автомобиля и воздуха, поэтому при её определении следует учитывать влияние ветра.
Точка приложения результирующей силы сопротивления воздуха Р w
(центр парусности) лежит в поперечной (лобовой) плоскости симметрии автомобиля. Высота расположения этого центра над опорной поверхностью дороги h w
оказывает значительное влияние на устойчивость автомобиля при движении его с высокими скоростями.
Увеличение Р w
может привести к тому, что продольный опрокидывающий момент Р w
·h w
настолько разгрузит передние колеса машины, что последняя потеряет управляемость вследствие плохого контакта управляемых колес с дорогой. Боковой ветер может вызвать занос автомобиля, который будет тем более вероятен, чем выше расположен центр парусности.
Попадающий в пространство между нижней части автомобиля и дорогой воздух создает дополнительное сопротивление движению за счет эффекта интенсивного образования вихрей. Для снижения этого сопротивления желательно передней части автомобиля придавать конфигурацию, которая препятствовала бы попадание встречного воздуха под его нижнюю часть.
По сравнению с одиночным автомобилем коэффициент сопротивления воздуха автопоезда с обычным прицепом выше на 20…30%, а с седельным прицепом – примерно на 10%. Антенна, зеркало внешнего вида, багажник над крышей, дополнительные фары и другие выступающие детали или открытые окна увеличивают сопротивление воздуха.
При скорости движения автомобиля до 40 км/ч
сила Р w
меньше силы сопротивления качению Р f
на асфальтированной дороге. При скоростях свыше 100 км/ч
сила сопротивления воздуха представляет собой основную составляющую тягового баланса автомобиля.
Грузовые автомобили имеют плохо обтекаемые формы с резкими углами и большим числом выступающих частей. Чтобы снизить Р w
, на грузовиках устанавливают над кабиной обтекатели и другие приспособления.
Подъемная аэродинамическая сила
. Появление подъемной аэродинамической силы обусловлено перепадом давлений воздуха на автомобиль снизу и сверху (по аналогии подъемной силы крыла самолета). Преобладание давления воздуха снизу над давлением сверху объясняется тем, что скорость воздушного потока, обтекающего автомобиль снизу, гораздо меньше, чем сверху. Значение подъемной аэродинамической силы не превышает 1,5% от веса самого автомобиля. Например, для легкового автомобиля ГАЗ-3102 «Волга» подъемная аэродинамическая сила при скорости движения 100 км/ч
составляет около 1,3% от собственного веса автомобиля.
Спортивным автомобилям, движущимся с большими скоростями, придают такую форму, при которой подъемная сила направлена вниз, которая прижимает автомобиль к дороге. Иногда с этой же целью такие автомобили оснащают специальными аэродинамическими плоскостями.
Решение.
Для
решения задачи рассмотрим физическую систему «тело – гравитационное поле Земли».
Тело будем считать материальной точкой, а гравитационное поле Земли — однородным. Выделенная физическая система
является незамкнутой, т.к. во время движения тела взаимодействует с воздухом.
Если не учитывать выталкивающую силу, действующую на тело со стороны воздуха,
то изменение полной механической энергии системы равняется работе силы
сопротивления воздуха, т.е.
∆
E
=
A c
.
Нулевой
уровень потенциальной энергии выберем на поверхности Земли. Единственной
внешней силой в отношении системы «тело – Земля» является сила сопротивления
воздуха, направленная вертикально вверх. Начальная энергия системы
E 1
, конечная
E 2
.
Работа
силы сопротивления
A.
Т.к.
угол между силой сопротивления и перемещением равен 180° , то косинус равен -1,
поэтому
A
= —
F c h
. Приравняем
A.
Рассматриваемую
незамкнутую физическую систему можно также описать теоремой от изменении
кинетической энергии системы взаимодействующих между собой объектов, согласно
которой изменение кинетической энергии системы равно работе, совершенной
внешними и внутренними силами при ее переходе из начального состояния в
конечное. Если не учитывать выталкивающую силу, действующую на тело со стороны
воздуха, а внутренней – сила тяжести. Следовательно
∆
E
к
=
A
1
+
A
2
, где
A
1
=
mgh
– работа силы тяжести,
A
2
=
F c hcos
180°
= —
F c h
– работа силы сопротивления;
∆
E
=
E
2
–
E
1
.
Работа силы на конечном пути
Для определения работы силы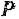 
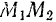
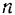
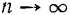
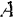
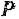
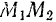
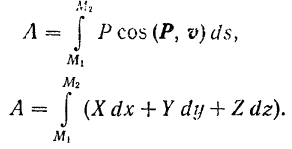
па каком-либо конечном перемещении 
(рис. 208) ее точки приложения разобьем это перемещение на 
перемещений, каждое из которых в пределе (при 
) переходит в элементарное. Тогда работа 
силы на конечном перемещении будет равна пределу суммы ее элементарных работ на всех бесконечно малых участках данного перемещения, и пользуясь формулами (187) и (189), получаем для нее следующие выражения:
Работа любой силы на любом конечном перемещении ее точки приложения равна взятому вдоль этого перемещения интегралу от элементарной работы.
Пределами интегралов в формулах (190) и (191) являются значения соответствующих переменных интегрирования в точках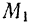 
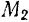
и 
.
Если точка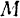 
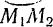
приложения силы перемещается по криволинейной траектории, то интегралы берутся вдоль соответствующей дуги 
этой траектории, т. е. являются криволинейными интегралами.
Если модуль касательной составляющей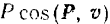 
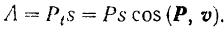
силы есть величина постоянная, то из формулы (190) будем иметь:
В частности, это всегда имеет место при прямолинейном движении точки под действием постоянной по модулю и направлению силы.
Работа постоянной силы при прямолинейном перемещении ее точки приложения равна произведению модуля силы на длину пути, пройденного ее точкой приложения, и на косинус угла между направлениями силы и перемещения ее точки приложения.
Если направление постоянной силы совпадает с па-правлением перемещения точки ее приложения или прямо противоположно направлению движения последней, то
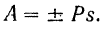
Формула (193) применима не только в случае прямолинейного перемещения точки приложения постоянной силы, но и в случае ее криволинейного движения, если только эта сила все время направлена по касательной к траектории ее точки приложения.
Работа силы имеет, очевидно, следующую размерность:
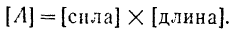
Так как в технической системе единиц сила измеряется в килограммах, а длина — в метрах, то работа в технической системе единиц измеряется в килограммометрах (кГм).
В системе СИ сила измеряется в ньютонах и длина в метрах, поэтому в этой системе за единицу работы принимается работа силы в н на пути, совпадающем с направлением силы, в 1 м. Эта единица работы называется джоулем (дж).
Найдем зависимость между килограммометром и джоулем. Ранее (стр. 242) было найдено, что сила в
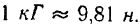
Следовательно,
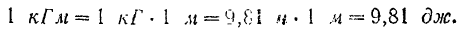
Один килограммометр равен 9,81 джоуля.
Пример задачи:
Тело совершает поступательное прямолинейное движение по закону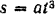 
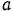
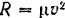
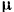
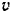
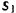
, где 
— некоторый постоянный коэффициент. Модуль силы сопротивления среды 
, где 
— коэффициент сопротивления среды и 
—скорость тела. Какую работу надо затратить на преодоление сопротивления среды при перемещении тела из состояния покоя на расстояние 
?
Решение:
Тело принимаем за материальную точку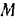 
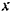
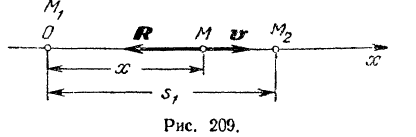
. Прямую, по которой движется эта точка (центр тяжести тела), принимаем за ось 
, направив ее в сторону движения топки (рис. 209).
Начало координат будет совпадать с начальным положением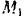 
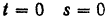
, точки (как видно из закона ее движения: при 
).
Найдем работу силы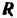 
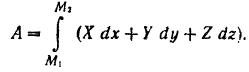
сопротивления среды, воспользовавшись для этого формулой (191):
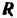
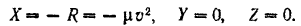
Так как сила сопротивления среды всегда направлена в сторону, противоположную движению тела, то ее проекциями на координатные оси будут:
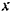
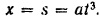
При выбранном направлении оси абсцисса точки
Элементарное приращение этой координаты
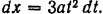
Скорость точки
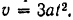
Подставляя найденные выражения в формулу (191), получим
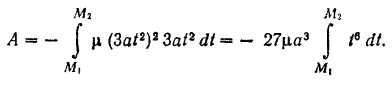
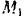
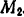
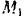
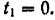
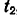
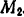
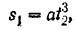
Так как подынтегральное выражение является функцией времени, то пределы интегрирования должны соответствовать значению этой переменной в точках и 
. Положению точки соответствует время 
Момент 
, соответствующий положению точки, находим из закона ее движения:
откуда
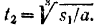
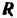
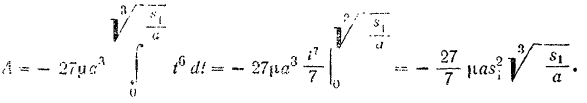
Таким образом, работа силы сопротивления среды на данном перемещении тела будет равна
Сила сопротивления среди направлена прогни движения тела потому се работа получилась отрицательной. Чтобы преодолеть эту силу на заданном перемещении тела, надо затратить такую же по величине, но положительную работу.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
Физика, 10 класс
Урок 13. Работа. Мощность. Энергия. Закон сохранения механической энергии
Перечень вопросов, рассматриваемых на уроке:
1. Работа
2. Мощность
3. Механическая энергия
4. Закон сохранения механической энергии.
Глоссарий по теме
Работа постоянной силы равна произведению модулей силы и перемещения точки приложения силы и косинуса угла между ними.
Мощность – отношение работы к интервалу времени, за который эта работа совершена.
Кинетическая энергия– энергия, которой обладает движущееся тело.
Кинетическая энергия материальной точки – величина равная половине произведения массы материальной точки на квадрат её скорости.
Теорема об изменении кинетической энергии: изменение кинетической энергии материальной точки при её перемещении равно работе, совершённой силой, действующей на точку при этом перемещении.
Если на точку действуют несколько сил, то изменение её кинетической энергии равно алгебраической сумме работ всех сил, действующих на неё.
Работа силы тяжести зависит только от положений начальной и конечной точек траектории и не зависит от формы траектории. При движении тела по замкнутой траектории работа силы тяжести равна нулю.
Консервативными силами называют силы, работа которых не зависит от формы траектории точки приложения силы и по замкнутой траектории равна нулю.
Работа силы упругости при растяжении пружины, т.е. когда направление силы противоположно перемещению тела, меньше нуля. Если начальное и конечное состояния пружины совпадают, то суммарная работа силы упругости при деформации пружины равна нулю.
Потенциальной энергией тела в поле силы тяжести называют величину, равную произведению массы тела на ускорение свободного падения и на высоту тела над поверхностью Земли.
Потенциальной энергией упругодеформированного тела называют величину, равную половине произведения коэффициента упругости тела на квадрат удлинения или сжатия.
Потенциальная энергия – энергия взаимодействия тел, обусловленная их взаимным расположением или взаимным расположением частей тела.
Полная механическая энергия равна сумме кинетической и потенциальной энергий тел, входящих в систему.
Закон сохранения энергии – энергия не создаётся и не уничтожается, а только превращается из одной формы в другую.
Основная и дополнительная литература по теме урока
Мякишев Г.Я., Буховцев Б.Б, Сотский Н.Н. Физика. 10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 131-147.
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009. С.49-56.
ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.
Теоретический материал для самостоятельного изучения
Влияние на тело сил, приводящее к изменению модуля их скорости, характеризуется величиной, которая зависит как от сил, так и от перемещения тел. Эта величина в механике называется работой силы, определяется по формуле:
Эта формула справедлива в случае, когда проекция силы на смещение постоянна.
Если есть угол между силой и смещением, то проекция силы равна произведению силы на косинус этого угла.
В этом случае работа постоянной силы равна произведению модулей силы и смещения точки приложения силы и косинуса угла между ними.
Работа по сравнению с силой и смещением — это не вектор, а скалярная величина. Она может быть, отрицательной равной нулю или положительной. Таким образом, знак работы определяется знаком косинуса угла между силой и перемещением.
Если сила F перпендикулярна перемещению тела, то работа, этой силой равна нулю. Это тот случай, когда действует сила, но тело не двигается.
Если на тело действует несколько сил, проекция результирующей силы на перемещение равна сумме проекций отдельных сил.
Fr = F1r+F2r+…
Поэтому суммарная работа, (алгебраическая сумма работ всех сил), равна работе результирующей силы.
В жизни важно те только совершение работы, но и время, за которое выполняется работа. Работу мы можем делать быстро и медленно. Отношение работы к временному интервалу, за который выполняется эта работа называется мощностью.
Как вы думаете, что необходимо для движения тела? Да, энергия необходима. Энергия характеризует способность тела (или системы тел) совершать работу. Кинетическая энергия – энергия, которой обладает движущееся тело
И энергия может быть кинетической и потенциальной.
Кинетическая энергия материальной точки равна половине массы материальной точки на квадрат её скорости:
Теорема об изменении кинетической энергии: изменение кинетической энергии материальной точки при её перемещении равно работе силы, действующей на точку во время этого перемещении.
Работа силы тяжести не зависит от формы траектории, а зависит только от положений начальной и конечной точек траектории
А = mgh1 – mgh2.
При движении тела по замкнутой траектории работа силы тяжести равна нулю.
Силы, работа которых не зависит от формы траектории точки приложения силы и на замкнутой траектории равна нулю, называют консервативными силами.
Работа при растяжении пружины силы упругости, когда направление силы совпадает с направлением движения тела, принимает положительные значения и определяется по формуле: 
В случае при увеличении деформации пружины, когда сила упругости, действующая на тело со стороны пружины, направлена противоположно деформации, работа силы упругости отрицательна:
Согласно теореме, об изменении кинетической энергии ΔЕк = Ек2 – Ек1 работа силы, действующей на тело, равна изменению его кинетической энергии:
Если силы взаимодействия между телами консервативны, то работу сил можно представить, как разность двух значений некоторой величины, зависящей от взаимного расположения тел или частей одного тела: А = mgh1 – mgh2, работы силы тяжести
и работы силы упругости.
Величина, равная произведению массы m тела на ускорение свободного падения g и высоту h тела над поверхностью Земли, называется потенциальной энергией тела в поле силы тяжести.
Закон сохранения механической энергии:
В изолированной системе, в которой действуют консервативные силы, механическая энергия сохраняется.
Е = Ек + Еп = const
Закон сохранения механической энергии является частным случаем общего закона сохранения энергии: энергия не создаётся и не разрушается, а преобразуется из одной формы в другую.
Примеры и разбор решения заданий
1.
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведён график зависимости проекции скорости vх тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение: по графику проекция скорости в момент времени 3с, равна 5 м/с. Мощность, развиваемая силой F для тела, движущегося со скоростью можно найти по формуле
Ответ: 10 Вт
2. Троллейбус массой 15 т трогается с места с ускорением 1,4 м/с2. Найти работу силы тяги и работу силы сопротивления на первых 10 м пути, если коэффициент сопротивления равен 0,05. Каково изменение кинетической энергии автобуса?
Дано:
m = 15т = 15 ·103кг
S = 10м
а = 1,4 м/с2
µ = 0,05
Найти: Ат; Ас; Ек
Запишем уравнение второго закона Ньютона:
в проекции на ось ОХ:
ma = Fт – Fтр
Fтр = µmg → Fт = ma + µmg = m(a+ µg);
По определению работы:
Ат = Fт S = m(a+ µg)S ;
Aт = 15 ·103 кг (1,4 м/с2+0,05 ·10 м/с2) ·10 м = 285 кДж
Работа силы сопротивления: Ас = -FтрS = — µmgS
Ас = -0,05·15·103 кг·10 м/с2·10м = -75 кДж
Кинетическая энергия определяется по формуле:
Ек = mv2/2. Скорость определим по формуле:
Ек = 15·103 кг·14 м/с2 = 210 кДж
Ответ: Ат = 285 кДж; Ас = -75 кДж; Ек = 210 кДж.