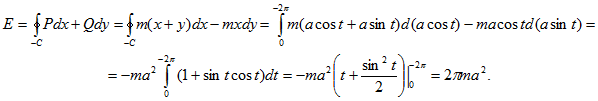Вычисление работы силового поля по перемещению материальной точки не обходится без применения криволинейного интеграла ІІ рода. Чтобы не повторять в каждой новой статье для криволинейных интегралов те же формулы сразу переходим к анализу готовых примеров.
Вычисление работы силового поля с помощью криволинейного интегралу ІІ рода
ЗАДАНИЕ 3.5 Вычислить работу силового поля 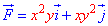
x2+y2=4 от точки A(2;0) к точке B(0;2).
Решение: Построим в декартовых координатах траекторию материальной точки вдоль круга L: x2+y2=4.
Уравнение верхней части полукруга и ее производной равны
В соответствии с точками A(2;0), B(0;2) пределы интегрирования изменяются от 2 до 0.
Не удивляйтесь, что не в обратном порядке. Их всегда нужно выписывать в порядке обхода контуру от точки A к B.
Робота силового поля F по перемещения материальной точки вдоль линии L вычисляется с помощью криволинейного интеграла ІІ рода :
Внимательно пересмотрите уравнение силового поля и подинтегральную функцию и Вам станет понятно, что и откуда берется. Как вычислить криволинейный интеграл детально расписано в предыдущих статьях (меняем y, dy на ф-и от «х» под интегралом).
ЗАДАНИЕ 3.10 Найти работу силового поля 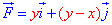
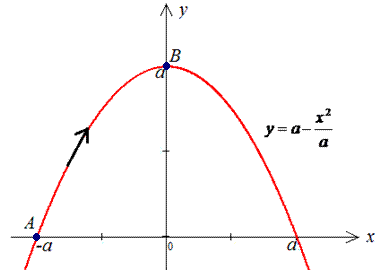
y=a-x2/a от точки A(-a;0) к точке B(0;a).
Решение: Имеем y=a-x2/a — уравнение параболы, находим дифференциал dy=-2x/a*dx и пределы изменения переменной
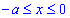
Вычисляем работу силового поля F, потраченную на перемещению материальной точки вдоль вдоль линии L
Криволинейный интеграл ІІ рода находим за первой формулой интегрирования.
ЗАДАНИЕ 3.12 Вычислить работу силового поля 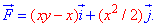
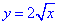
Решение: Строим траекторию материальной точки вдоль корневой функции L: 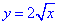
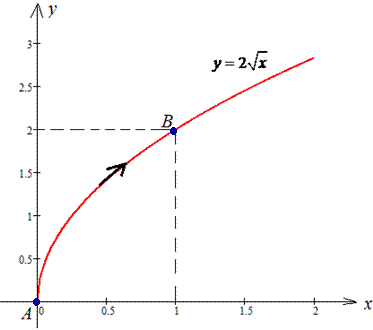
Записываем производную 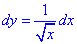
Находим роботу A силового поля F : 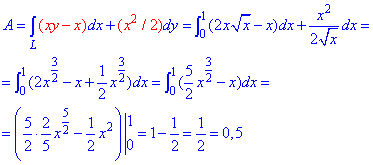
Перед интегрированием превращаем корни к показательной форме записи, а дальше вычисляем за табличными формулами интеграл.
ЗАДАНИЕ 3.14 Вычислить работу силового поля 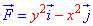
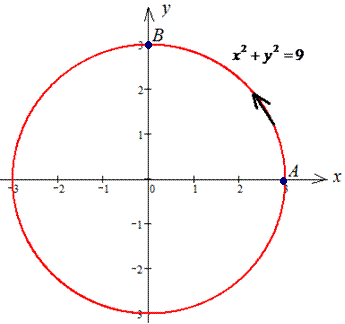
x2+y2=9.
Решение: Наведем траекторию движения материальной точки по кругу L: x2+y2=9.
Верхняя ветка ограничена функцией
Аргумент изменяется от 3 до 0
Работа А силового поля F при перемещению материальной точки вдоль линии L вычисляется с помощью криволинейного интеграла ІІ рода :
Интегрирование само по себе тяжелое, главное правильно найти дифференциал функции и не ошибиться с пределами интегрирования.
ЗАДАНИЕ 3.19 Вычислить работу силового поля 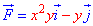
прямая от точки A(-1;0) к точке B(0;1).
Решение: Запишем уравнение прямой, которая проходит через две точки A(-1;0) и B(0;1):
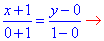
отсюда y=x+1.
Таким образом, имеем дифференциал дуги dy=dx плюс интервал интегрирования [- 1;0].
График прямой приведен на рисунку ниже
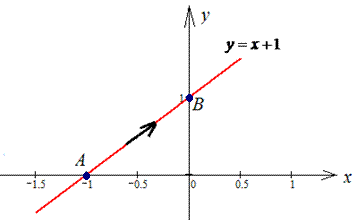
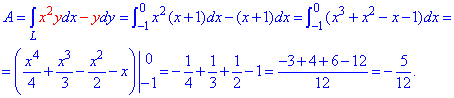
Криволинейный интеграл 2 рода легко сводим к определенному и находим результирующее значение работы.
ЗАДАНИЕ 3.20 Вычислить работу силового поля 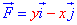
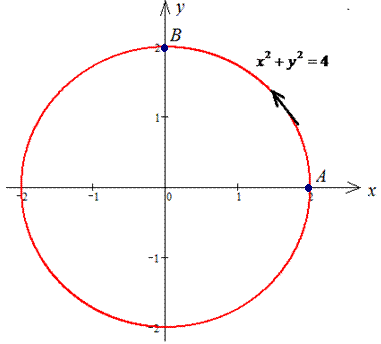
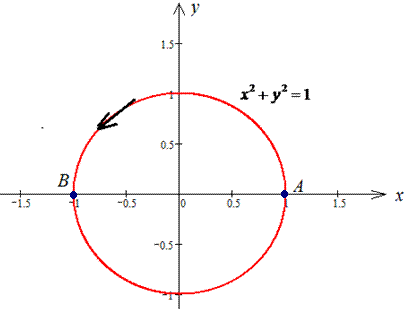
x2+y2=1 от точки A (1;0) к точке B (- 1;0).
Решение: Построим траекторию материальной точки против движения часовой стрелки по кругу L: x2+y2=9.
Верхнюю его дуга предствим корневой зависимостью
Аргумент при этом изменяется от 1 к -1.
Работа силового поля потрачена на перемещение материальной точки вдоль дуги круга равна интегралу:
Во время интегрирования получим арксинус, который на границах дает число Pi/2.
Еще один раздел где можно применить криволинейный интеграл ІІ рода теперь доступный и известный Вам.
Будьте внимательные в вычислениях и успешной Вам учебы!
6.4.1. Работа силового поля, криволинейный интеграл второго рода
Рассмотрим силовое
поле на плоскости
.
Под
действием силы
от точки А
до точки В
по кривой L
движется точка. Требуется вычислить
работу, совершаемую силой
на пути L
(рис. 6.4.1).
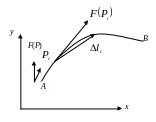
Рис.
6.4.1. Криволинейное движение точки на
плоскости xoy
под действием переменной силы F

Рис.
6.4.2. Прямолинейное движение точки под
действием постоянной силы
Для
прямолинейного
движения и постоянной
силы (
=const)
работа, совершаемая на отрезке
(рис. 6.4.1), равна скалярному произведению
векторов
и l:

где
l
– направленный отрезок, длина которого
равна пройденному пути.
Чтобы
найти работу переменной силы
(x,y)
на криволинейном участке пути L
от А
до В,
очевидно, этот путь нужно разбить на k
маленьких частей так, чтобы каждый
участок пути можно было заменить
направленным отрезком
,
а силу на нем считать постоянной и равной
(Рi)=const
(рис. 6.4.2).
Тогда
работа, совершаемая силовым полем на
i-ом
элементарном участке длиной
приближенно
будет равна скалярному произведению
векторов
Аi
(
(Рi))
.
Вся
работа на пути L
равна сумме элементарных работ
Переходя
к пределу при max
0,
получим точное значение работы,
совершаемой силовым полем на пути L:
Предел,
если он существует, называют криволинейным
интегралом второго
рода, обозначают
,
где
– предельное значение элементарного
направленного отрезка
.
Очевидно, направление
будет совпадать с направлением касательной
к кривой L,
а его модуль равен дифференциалу длины
дуги –
.
Обозначим единичный вектор касательной
–
,
тогда
.
Определение
1. Работа
силового поля
на криволинейном пути L
равна криволинейному интегралу по
кривой L
от скалярного произведения вектора
поля и
–
элемента касательной
к кривой.
,
) (6.4.1)
Выражение
,
)
– называют векторной
формой
криволинейного интеграла второго
рода или
линейным интегралом вектора
.
Скалярное
произведение двух векторов
{P(x,y),
Q(x,y)}
и
{dx,
dy}
можно выразить через их координаты:
(6.4.2)
Правая
часть равенства (6.4.2) представляет собой
координатную
форму
криволинейного интеграла второго рода.
Для пространственной кривой она имеет
вид:
(6.4.3)
Следует
особо подчеркнуть разницу между
физическим смыслом интеграла
– вектора
(второго
рода) и интеграла первого рода
по длине
дуги, который был рассмотрен ранее.
В
последнем суммируются значения скалярной
функции
f(x,y,z),
например, плотности массы или заряда,
умноженные на
–
меры элементарных частей кривой L
(дифференциалы длины дуги), на которые
она дробится. Поэтому, криволинейный
интеграл первого рода не зависит от
того, в каком направлении проходится
кривая L.
Под знаком
криволинейного интеграла второго рода
стоит
скалярное произведение двух векторов,
вектора поля
и элемента касательной
,
при этом направление касательной должно
совпадать с выбранным направлением
обхода кривой
L.
Таким образом, в линейном интеграле
вектора
суммируются значения проекций векторной
величины на касательную к кривой в
различных ее точках. Поскольку скалярное
произведение
зависит от угла между векторами
и
знак интеграла
будет зависеть от выбранного обхода
линии L.
Криволинейный интеграл вектора
вычисляют
так же, как криволинейный интеграл
первого рода, т.е. путем сведения к
линейному (определенному) интегралу.
Для этого должно быть задано уравнение
линии L
и направление
ее обхода (либо
координаты начальной и конечной точек).
Если
плоская линия L
задана в
декартовой системе координат уравнением
у=у(х),
то при сведении интеграла
к
линейному, переменную у
и dy
заменяют их выражением через х
из уравнения линии L:
y
= y(x),
dy
=
dx.
При
параметрическом задании линии L:
x=x(t);
y=y(t),
замену переменных, приводящую к линейному
интегралу, осуществляют по формулам:
х=x(t);
dx=
dt;
y=y(t);
dy=
dt.
Пример
1. Вычислить
работу силового поля
{cosy,
siny}
на
отрезке прямой, соединяющей точки А(2;
–2), В(–2,
2).
Решение.
Работа силового поля равна интегралу
Уравнение
линии L,
проходящей через точки А(2;
–2), В(–2;
2), имеет вид y
= – x
(рис. 6.4.3).
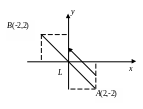
Рис.
6.4.3.
Прямолинейный путь в силовом поле
(иллюстрация к примеру)
Дифференциал
на этой линии dy=–dx.
Переменная х
меняется от 2 до – 2.
Подставляя
в криволинейный интеграл вместо у
– уравнение линии, и заменяя dy
на –
dx
получим
,
,
А
= – 2sin(2рад)
= – 2sin1140
= – 1,827.
В
данном случае работа отрицательна. Она
совершается в направлении, обратном
вектору поля.
Пример
2. Вычислить
криволинейный интеграл
,
где
L
– верхняя часть эллипса
,
обход которого проводится по часовой
стрелке (рис. 6.4.4).
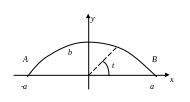
Рис.
6.4.4.
Криволинейный путь в плоском силовом
поле (иллюстрация к примеру)
Решение.
Уравнение эллипса лучше взять в
параметрической форме
L:
x=acost;
y=bsint.
В
этом случае вычисления будут значительно
проще. Найдем значения параметра в
точках начала и конца обхода: в точке
А(–
а;
0) t1
= ,
в точке В(а;
0) t2
= 0.
Выразим
дифференциалы dx
и dy
на данной линии через параметр t:
dx=–asintdt;
dy=bcostdt.
Заменяя
в криволинейном интеграле переменные
х
и у
параметрическим уравнением эллипса и
дифференциалы dx
и dy,
найденными для них значениями на эллипсе,
получим:
=
,
,
.
Таким
образом, при обходе верхней части эллипса
под действием силового поля
,
совершается положительная работа.
Пример
3. Вычислить
криволинейный интеграл
,
где
L
– дуга параболы от точки А(0;0)
до точки В(2;4).
Решение.
Векторное поле параллельно оси ox:
.
Преобразуем криволинейный интеграл в
линейный, т.е. переменную y
заменим уравнением параболы
и расставим пределы изменения х
при движении от точки А
до точки В:
.
Вычисляя данный
интеграл, получим:
.
Работа,
совершаемая силовым полем
на данном отрезке параболы, отрицательна.
Пример
4. Вычислить
криволинейный интеграл
где
L
– дуга параболы у=х2
от точки А(0;0)
до точки В(1;1).
Решение.
Координаты вектора силового поля:
.
Уравнение
линии L:
у=х2.
Дифференциал на этой линии dy=2xdx.
Пределы изменения переменной х:
0; 1. Перейдем к линейному интегралу:
.
Вычисляя линейный
интеграл, получим:
.
Данное
поле на отрезке параболы совершает
положительную работу.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сообщения без ответов | Активные темы
Найти работу силового поля вдоль дуги плоской кривой
Модераторы: Prokop, mad_math
| Автор | Сообщение | ||
|---|---|---|---|
|
botanik007 |
|
||
|
Подскажите, как такие решать, особенно второй. 1. Найти работу силового поля [math]mathbf{F}(x,y)=x^2mathbf{i}+frac{1}{y^2}mathbf{j}[/math] вдоль дуги плоской кривой [math]xy=1[/math] заключенной между точками (1;1) и (4;1/4) Напишите, пожалуйста, алгоритм и по возможности решение.
|
||
| Вернуться к началу |
|
||
|
botanik007 |
|
||
|
спасибо )
|
|||
| Вернуться к началу |
|
||
|
mad_math |
|
||
|
1. [math]P(x,y)=x^2,Q(x,y)=frac{1}{y^2},AB:y=frac{1}{x},1leq xleq 4[/math]
|
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю mad_math «Спасибо» сказали: Medvedo |
|||
|
botanik007 |
|
||
|
спасибо
|
|||
| Вернуться к началу |
|
||
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти работу поля F вдоль дуги AB кривой Г, если
в форуме Интегральное исчисление |
haykaz1898 |
3 |
785 |
25 апр 2018, 12:52 |
|
Найти работу силового поля
в форуме Интегральное исчисление |
Ryslannn |
11 |
1611 |
29 ноя 2017, 16:32 |
|
Вычислить работу силового поля
в форуме Интегральное исчисление |
kicultanya |
0 |
320 |
05 окт 2018, 20:04 |
|
Найти работу поля вдоль винтовой линии
в форуме Векторный анализ и Теория поля |
DIDG |
0 |
691 |
21 фев 2014, 14:43 |
|
Найти длину дуги плоской кривой ау^2=х^3 0<=x<=5a
в форуме Интегральное исчисление |
karinakarina |
1 |
327 |
13 дек 2016, 21:02 |
|
Длина дуги плоской кривой
в форуме Интегральное исчисление |
kusya |
1 |
205 |
27 ноя 2016, 14:32 |
|
Площадь плоской фигуры и длина дуги кривой
в форуме Интегральное исчисление |
IvanKnyshov1996 |
2 |
486 |
26 апр 2015, 21:57 |
|
Работа силового поля
в форуме Интегральное исчисление |
paul_woker |
4 |
258 |
02 май 2020, 19:58 |
|
Работа силового поля
в форуме Интегральное исчисление |
Ryslannn |
8 |
414 |
30 ноя 2017, 15:09 |
|
Найти циркуляцию векторного поля F(-y,x) вдоль кардиоиды
в форуме Векторный анализ и Теория поля |
Linc |
1 |
230 |
22 ноя 2021, 16:29 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 4 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
Содержание:
Потенциальное силовое поле:
Для вычисления работы силы на каком-либо перемещении в общем случае необходимо знать закон движения точки на этом перемещении. Есть класс сил, для которых работа не зависит от характера движения точки на рассматриваемом перемещении. Эти силы называют потенциальными, и они имеют важное значение в различных областях механики и физики.
Потенциальное силовое поле и силовая функция
Силовым полем называют часть пространства, в каждой точке которого на материальную точку действует определенная сила, зависящая от координат точки и времени. Силовое поле считают стационарным, если действующие силы не зависят от времени. Если же силы зависят от времени, то силовое поле является нестационарным.
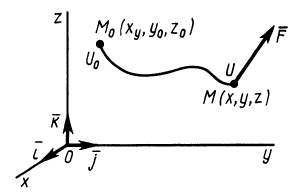
Силовое поле называют потенциальным, если имеется силовая функция
Функцию 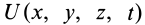
Рис. 72
Рассмотрим основные свойства силовой функции стационарного силового поля. Из (77) следует, что силовая функция определяется с точностью до постоянной, так как для проекций силы на координатные оси требуются только частные производные по координатам от этой функции и добавление постоянной к функции 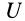
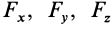
т. e.
Таким образом, элементарная работа силы в потенциальном силовом поле равна полному дифференциалу от силовой функции. Иногда это свойство силовой функции принимают за ее определение; тогда (77) получают из (78).
Полная работа силы 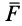
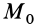
т.е.
где
Следовательно, полная работа силы на каком-либо перемещении точки равна разности значений силовой функции в конечной и начальной точках перемещения и не зависит от формы траектории, по которой оно совершается, если силовая функция является однозначной.
Из (79) следует, что работа силы в потенциальном силовом поле по любому замкнутому пути равна нулю, так как значение силовой функции в начальной и конечной точках перемещения одинаково, если силовая функция не принимает других значений после возвращения в первоначальную точку.
Силовая функция может принимать другие значения после возвращения в первоначальную точку в зависимости от количества обходов, если область, ограниченная замкнутым путем обхода, содержит в себе специальные особые точки силовой функции.
Если применить понятие вектор-градиента от скалярной функции
где 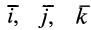
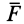
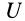
Определим условия, которые позволяют по силам силового поля устанавливать, будет ли силовое поле потенциальным.
Если силовая функция 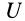
Так как
то
Аналогично,
Таким образом, полученные условия имеют вид
В векторном исчислении доказывается, что условия (80) не только необходимы, но и достаточны для существования силовой функции. Если использовать вектор вихря 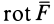
то условия (80) можно выразить более кратко:
Таким образом, для того чтобы силовое поле было потенциальным, необходимо и достаточно, чтобы оно было безвихревым.
Непотенциальными силами являются силы сопротивления, зависящие от скорости, и силы трения. Силы сухого трения не будут потенциальными, так как хотя сила трения постоянна и не зависит от скорости, но направление силы трения от скорости зависит.
- Заказать решение задач по теоретической механике
Поверхности уровня и силовые линии
Если рассматривать точки потенциального силового поля, в которых силовая функция имеет одно и то же значение, например 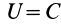
Уравнение поверхности уровня имеет вид
Отметим некоторые свойства поверхностей уровня.
1. Работа силы равна нулю, если начальная и конечная точки перемещения лежат на одной поверхности уровня. Действительно,
Если начальная и конечная точки лежат на одной поверхности уровня, то 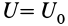
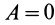
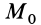
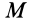
2. Сила в потенциальном силовом поле всегда перпендикулярна поверхности уровня или, точнее, касательной плоскости поверхности уровня. Действительно, пусть имеем поверхность уровня 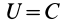
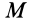
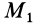
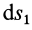
С другой стороны,
Так как 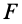
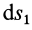
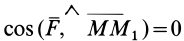
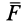
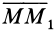
3. Сила в потенциальном силовом поле всегда направлена в сторону возрастающих значений силовой функции. Для
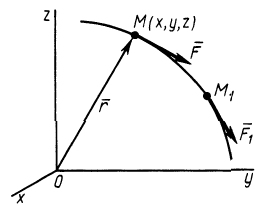
доказательства этого свойства силы возьмем точку 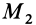
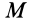
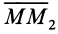
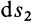
так как 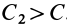
Рис. 73
Следовательно,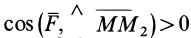
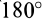
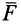
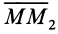
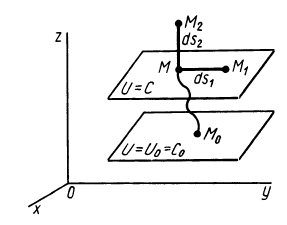
4. Если все силовое поле разбить поверхностями уровня на 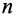
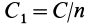
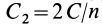
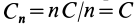
Рис. 74
Наряду с поверхностями уровня в силовом поле вводят понятие силовой линии, т. е. такой линии, в каждой точке которой сила направлена по касательной к этой линии (рис. 74). Так как вектор 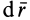
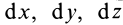
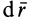
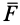
Эти дифференциальные уравнения относительно координат 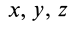
Потенциальная энергия
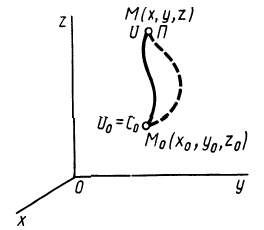
В случае потенциального силового поля наряду с силовой функцией можно ввести другую функцию, характеризующую запас энергии в данной точке поля,— потенциальную энергию в этой точке (рис. 75), или потенциальную энергию материальной точки в рассматриваемой точке силового поля.
Потенциальной энергией 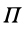
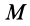
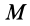
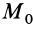
или
Рис. 75
Постоянная 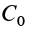
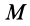
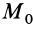
На основании (77) и (82) имеем:
Из (78), (79) и (82) соответственно получаем
Из приведенных формул следует, что 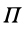
или
Потенциальную энергию в какой-либо точке поля с точностью до произвольной постоянной можно определить как значение силовой функции в этой же точке, взятое со знаком минус. По существу, достаточно одной из функций 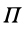
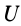
Понятие потенциальной энергии было введено раньше, чем силовая функция. Силовая функция более удобна, так как некоторые формулы, содеражащие эту функцию, не имеют знака минус.
Примеры вычисления силовых функций
Если вычислить силовую функцию, то на основании (82′) будет известна и потенциальная энергия. Вычислим силовые функции однородного поля силы тяжести, силового поля линейной силы упругости и силового поля силы притяжения, действующей по закону Ньютона.
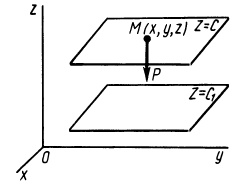
Силовая функция однородного поля силы тяжести. Если ось 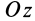
Вычисляя элементарную работу силы 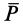
Так как элементарная работа является полным дифференциалом, то силовое поле силы тяжести является потенциальным и силовая функция этого поля определяется по формуле
По формуле (83) определяют силовую функцию однородного поля силы тяжести, т. е. поля, в котором сила тяжести постоянна по модулю и направлению. Уравнение поверхности уровня 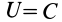
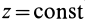
Рис. 76
Силовая функция линейной силы упругости
Для линейной силы упругости (см. рис. 62) имеем:
Следовательно
так как 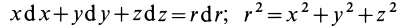
Силовую функцию линейной силы упругости определяют по формуле
Поверхностями уровня 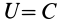
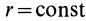
Силовая функция силы притяжения по закону Ньютона
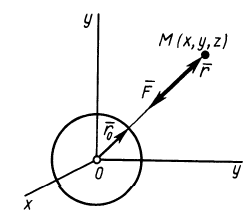
Вычислим силовую функцию поля земного притяжения. Если выбрать начало координат в центре Земли (рис. 77), то сила притяжения точки земным шаром 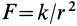
Сила F направлена к центру Земли; следовательно, вводя единичный вектор 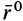
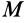
Проецируя силу 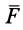
Тогда
так как 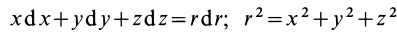
Рис. 77
Таким образом, силовая функция силы притяжения, по закону Ньютона,
Постоянную 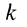
где 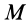
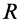
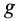
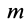
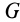
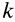
Силовая функция и потенциальная энергия системы
Для механической системы в потенциальном силовом поле можно ввести силовую функцию как функцию, зависящую от координат всех точек системы, т. е. от положения системы в силовом поле. Если система состоит из 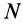
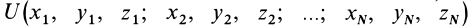
Сумма элементарных работ всех сил, действующих на точки системы, определяется по формуле
или
Таким образом, сумма элементарных работ сил поля, действующих на механическую систему, равна полному дифференциалу от силовой функции. Если вычислить сумму работ, которую совершат силы поля, действующие на механическую систему при перемещении системы из положения 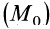
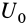
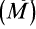
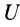
или
Следовательно, сумма работ сил поля, действующих на систему при перемещении системы из одного начального положения в другое, равна разности значений силовой функции в конечном и начальном положениях системы.
Потенциальной энергией системы 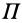
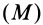
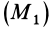
где 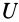
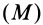
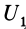
Из (86) — (89) следует:
- Закон сохранения механической энергии
- Принцип Даламбера
- Динамические реакции при вращении твердого тела вокруг неподвижной оси
- Векторное исчисление
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Теорема об изменении кинетического момента
- Теорема об изменении кинетической энергии
Рабчук Александр Викторович1, Самигуллина Ракия Гареевна2
1Уфимский государственный авиационный технический университет, к.т.н.. доцент кафедры математики
2Уфимский государственный авиационный технический университет, старший преподаватель каф. математики
Аннотация
Традиционно, такие разделы высшей математики как криволинейные и поверхностные интегралы, особенно их применение, вызывают затруднения у студентов при изучении. Поэтому в данной статье кратко дана теория и приведено много разобранных примеров взятых из различных источников, в частности из [1,2,3].
Rabchuk Aleksandr Viktorovich1, Samigullina Rakiya Gareevna2
1Ufa State Aviation Technical University, PhD in Technical Science, Assistant Professor of the Mathematic Department
2Ufa State Aviation Technical University, Senior teacher of the Mathematic Department
Abstract
By tradition, devides higher mathematics by contour and surface integrals ,particularly application, is difficult by students.Therefor in this article give theori and many look into examples from [1,2,3].
Библиографическая ссылка на статью:
Рабчук А.В., Самигуллина Р.Г. Приложения криволинейных интегралов. Часть 1 // Современная педагогика. 2014. № 10 [Электронный ресурс]. URL: https://pedagogika.snauka.ru/2014/10/2675 (дата обращения: 24.02.2023).
Приложения криволинейного интеграла первого рода
1. Если подынтегральная функция равна единиц, то криволинейный интеграл
равен длине S кривой L, т.е.
2. Пусть в плоскости Оху задана гладкая кривая L, на которой определена и непрерывна функция двух переменных z=f(x,y)≥0. Тогда можно построить цилиндрическую поверхность с направляющей L и образующей, параллельной оси Оz и заключенной между L и поверхностью z=f(x,y). Площадь этой цилиндрической поверхности можно вычислить по формуле
3. Если L=AB – материальная кривая с плотностью, равной ρ=ρ(х,у), то масса этой кривой вычисляется по формуле
(физический смысл криволинейного интеграла первого рода).
4. Статистические моменты материальной кривой L относительно координатных осей Ох и Оу соответственно равны
где ρ(х,у) – плотность распределения кривой L а
— координаты центра тяжести (центра масс) кривой L.
5. Интегралы
выражают моменты инерции кривой L с линейной плотностью ρ(х,у) относительно осей Ох, Оу и начала координат соответственно.
ПРИМЕРЫ:1. Вычислить криволинейный интеграл
где L – дуга параболы у2 = 2х, заключенная между точками (2, 2) и (8, 4).
Найдем дифференциал дуги dl для кривой
. Имеем
Следовательно, данный интеграл равен
Ответ:
2. Вычислить криволинейный интеграл
где L – контур треугольника АВО с вершинами А(1,0), В(0,1), О(0,0)
Поскольку
то остается вычислить криволинейный интеграл по каждому из отрезков АВ, ВО и ОА :
1) (АВ): так как уравнение прямой АВ имеет вид у=1 – х, то . Отсюда, учитывая, что х меняется от 0 до 1, получим
2) (ВО): рассуждая аналогично, находим х=0, 0 ≤ у ≤ 1, откуда
3) (ОА):
.
4) Окончательно
Ответ:
3. Вычислить криволинейный интеграл
где L – окружность
Введем полярные координаты
Тогда, поскольку
уравнение окружности примет вид
т.е.
а дифференциал дуги
При этом Следовательно,
Ответ:
4. Вычислить криволинейный интеграл первого рода от функции с тремя переменными
где L – дуга кривой, заданной параметрически
Перейдем в подынтегральном выражении к переменной t. Имеем для подынтегральной функции:
Теперь выразим через t дифференциал dl:
Таким образом,
Ответ:
5. Вычислить площадь части боковой поверхности кругового цилиндра , ограниченной снизу плоскостью Оху, а сверху поверхностью
Искомая площадь вычисляется по формуле
где L – окружность x2+y2=R2. Поверхность цилиндра и поверхность симметричны относительно координатных плоскостей Оxz и Oyz, поэтому можно ограничиться вычислением интеграла при условиях у≥0, х≥0, т.е. вычислить четверть искомой площади и результат умножить на 4. Имеем
Следовательно,
Получили определенный интеграл, который берем подстановкой
откуда
Ответ:
6. Найти массу четверти эллипса
расположенной в первой четверти, если линейная плотность в каждой точке пропорциональна ординате этой точки с коэффициентом k.
Поскольку р(х, у)=ky, имеем
L – четверть эллипса
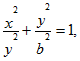
Переходим к параметрическим координатам эллипса Напомним, что
— фокусное расстояние эллипса, а
— эксцентриситет эллипса. Находим
Переходим к вычислению массы
Воспользуемся формулой
где Получаем
Учитывая, что 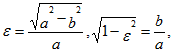
Ответ: .gif)
7. Найти координаты центра тяжести дуги окружности x2+y2=R2(0≤ x ≤R, 0≤ y ≤R).
Так как по условию задана четверть дуги окружности, то ее длина
В силу того, что биссектриса I координатного угла является осью симметрии, имеем
. Теперь находим
Ответ:
Приложения криволинейного интеграла второго рода
Интеграл
можно представить в виде скалярного произведения векторов F=Pi+Qi и ds=idx+jdy:
В таком случае
Выражает работу переменной силы F=Pi+Qj при перемещении материальной точки М=М(х,у) вдоль кривой L=AB от точки А до точки В.
При А=В кривая L замкнута, а соответствующий криволинейный интеграл по замкнутой кривой обозначается так:
В этом случае направление обхода контура иногда поясняется стрелкой на кружке, расположенном на знаке интеграла.
Предположим, что в плоскости Оху имеется односвязная область D (это значит, что в ней нет «дыр»), ограниченная кривой , (
— обозначение границы области D), а в области D и на ее границе
функции Р(х,у) и Q(х,у) непрерывны вместе со своими частными производными.
Теорема: Пусть А и В – произвольные точки области D, AmB и AnB – два произвольных пути (гладкие кривые), соединяющие эти точки (рис. 2).
Тогда следующие условия равносильны:
1. (условие Грина).
2. (криволинейный интеграл не зависит от пути интегрирования).
3. (интеграл по любому замкнутому пути равен нулю).
4. (выражение
представляет собой полный дифференциал некоторой функции
).
В случае выполнения любого из равносильных условий предыдущей теоремы криволинейный интеграл по любой кривой, соединяющей точки (хо, уо) и (х1, у1) из области D, можно вычислить при помощи формулы Ньютона-Лейбница
где U(x, y) – некоторая первообразная для P dx + Q dy.
С другой стороны, первообразная U(x, y) выражения P dx + Q dy может быть найдена при помощи криволинейного интеграла
В этих же условиях на функции Р(х,у) и Q(х,у), а также на область D, имеет место формула Грина, позволяющая свести криволинейный интеграл по замкнутому контуру к двойному интегралу
Здесь предполагается, что обход границы области D в криволинейном интеграле
совершается в положительном направлении, т.е. при таком обходе границы область D остается слева; для односвязной области это направление совпадает с направлением против часовой стрелки.
Заметим, что площадь S=S(D) области D может быть вычислена при помощи криволинейного интеграла второговрода:
(эта формула получается из формулы Грина с ).
ПРИМЕРЫ:1. Даны функции Р(х ,у) = 8х+4у+2, Q(х ,у) = 8у+2 и точки А(3, 6), В(3,0), С(0,6). Вычислить криволинейный интеграл
где:
1) L – отрезок ОА;
2) L – ломаная ОВА;
3) L – ломаная ОСА;
4) L – парабола, симметричная относительно оси Оу и проходящая через точки О и А;
5) проверить выполнимость условия Грина.
1) Отрезок ОА может быть записан в виде: у=2х, . Тогда dy=2dx и
2) Используем свойство аддитивности, вычисляя отдельно интеграл по отрезкам ОВ и ВА. Тогда:
а) ОВ: здесь у=0, 0≤х≤3, т.е. dy=0, откуда
б) ВА: х=3, 0≤у≤6, т.е. dx=0, и
Таким образом,
3) Этот интеграл вычислим аналогично предыдущему.
а) ОС: х=0, (т.е. dx=0), 0≤y≤6, откуда
б) СА: 0≤х≤3 , у=6, dy=0, следовательно,
Окончательно
4) Подставив координаты точки А(3;6) в равенство у=ах2 найдем уравнение данной параболы . При этом 0≤х≤3 и
откуда (путь ОА по параболе обозначим
)
5) Имеем
т.е. условие Грина не выполняется. Этот факт, а также вычисления в пунктах 1) – 4) этой задачи показывают, что данный криволинейный интеграл второго рода зависит от пути интегрирования.
2. Вычислить интеграл
где L – верхняя половина эллипса .gif)
Воспользуемся параметрическими уравнениями эллипса: х=a cost, y=b sin t,
т.е. dx = – a sin t dt, dy = b cos t dt. Подставляя в интеграл и учитывая направление обхода (откуда следует, что t меняется от π до 0), получаем
.gif)
3. Вычислить криволинейный интеграл
где L – отрезок, соединяющий точку С(2, 3, -1) с точкой D(3, -2, 0).
Составим параметрические уравнения отрезка СD, используя уравнения прямой, проходящей через две точки:
Отсюда . Далее, находим
подставляем все нужные выражения в данный интеграл, обозначенный через J, и вычисляем определенный интеграл:
Ответ:
4. Вычислить где К – отрезок прямой от А(0 ;0) до В (4; 3).
Уравнение прямой АВ имеет вид у=(3; 4)х. Находим у/= ¾ и, следовательно,
Ответ:
5. Вычислить если
Найдем
Тогда
Ответ:
6. Найти массу М дуги кривой x=t, y=t2/2, z=t3/3 (0≤ t ≤1), линейная плотность которой меняется по закону
Ответ:
7. Вычислить криволинейный интеграл от точки А(1, 0) до точки В(0, 2) (рис. 3):
1) по прямой 2х+у=2;
2) по дуге параболы 4х+у2=4;
3) по дуге эллипса x=cost, y=2sint.
1) Пользуясь данным уравнением линии интегрирования, преобразуем криволинейный интеграл в обыкновенный определенный интеграл с переменной х, затем вычисляем его:
у=2-2х, dy=-2dx,
2) Здесь удобно преобразовать криволинейный интеграл в обыкновенный интеграл с переменной у:
3) Преобразуем данный интеграл в обыкновенный с переменной t, затем вычисляем его: x=cost, dx=-sintdt; y=2sint; dy=2costdt:
Ответ: I1=1, I2=-1/5, I3=4/3.
8. Вычислить криволинейный интеграл между точками Е
(-1, 0) и Н (0, 1):
1) по прямой ЕН;
2) по дуге астроиды х=cos3t, y=sin3t.
1) Вначале составляем уравнение линии интегрирования – прямой ЕН, как уравнение прямой, проходящей через две известные точки: у-х=1.
Пользуясь этим уравнением и известной формулой для дифференциала дуги плоской кривой преобразуем данный криволинейный интеграл в обыкновенный интеграл с переменной х и вычисляем его:
2) Преобразуем данный интеграл в обыкновенный с переменной t, затем вычисляем:
ибо π/2≤ t ≤π;
Ответ:
9. Даны точки А(3, -6, 0) и В(-2, 4, 5). Вычислить криволинейный интеграл
1) по прямолинейному отрезку ОВ;
2) по дуге АВ окружности, заданной уравнениями x2+y2+z2=45, 2x+y=0.
1) Вначале составляем уравнения линии интегрирования – прямой ОВ.
Пользуясь общими уравнениями прямой, проходящей через две точки .gif)
Приравнивая эти равные отношения параметру t, преобразуем полученные канонические уравнения прямой ОВ к параметрическому виду: x=-2t, y=4t, z=5t.
Далее, пользуясь этими уравнениями, преобразуем данный криволинейный интеграл в обыкновенный интеграл с переменной t, затем вычисляем его
2) Преобразуем данные уравнения окружности к параметрическому виду. Полагая х=t, получим у=-2t (из второго данного уравнения), (из первого уравнения). Отсюда
.gif)
Ответ:
10. Вычислить криволинейные интегралы:
1)
2) вдоль периметра треугольника с
вершинами А(-1,0), В (0,2) и С (2,0)
Составив уравнение прямой АВ, у-2х=2, и исходя из этого уравнения, преобразуем криволинейный интеграл на отрезке АВ в обыкновенный интеграл с переменной х:
у=2х+2, dy=2dx,
Аналогичным путем вычисляя криволинейный интеграл на отрезках ВС и СА, получим
х=2-у, dx=-dy,
Следовательно,
2) Здесь подынтегральное выражение есть полный дифференциал функции двух переменных, ибо (уcosx)’y =(sinx)’x =cosx. Вследствии этого данный криволинейный интеграл, взятый по периметру данного треугольника равен нулю. Он будет равен нулю и по любому другому замкнутому контуру.
Ответ:
11. Найти длину кардиоиды x=2acost-acos2t, y=2asint-asin2t.
Применяем формулу
, исходя из данных параметрических уравнений кардиоиды и формулы для дифференциала дуги плоской кривой, преобразуем криволинейный интеграл формулы в обыкновенный интеграл с переменной t.
Ответ: L=16a.
12. Найти площадь, ограниченную замкнутой кривой:
1) эллипсом x=a cost, y=b sint;
2) петлей декартова листа х3+у3-3аху=0.
1) Применяем формулу
, исходя из данных параметрических уравнений эллипса, преобразуем криволинейный интеграл в обыкновенный интеграл с переменной t и вычисляем его:
2) Вначале преобразуем данное уравнение к параметрическому виду. Полагая у=хt, получим
Геометрический параметр t=y/x есть угловой коэффициент полярного радиуса ОМ (рис. 6), точка М(х, у) опишет всю петлю кривой при изменении t от 0 до +∞.
Преобразуя криволинейный интеграл формулы в обыкновенный интеграл с переменной t , получим
Ответ: S=3a2/2.
13. Найти массу дуги АВ кривой у=lnx, если в каждой ее точке линейная плотность пропорциональна квадрату абсциссы точки: хА=1, хВ=3.
Применяем формулу
, исходя из данного уравнения кривой, преобразуем криволинейный интеграл в обыкновенный с переменной х
Ответ:
14. Найти координаты центра тяжести дуги АВ винтовой линии х=аcost, y=asint, z=bt, если в каждой ее точке линейная плотность пропорциональна аппликате этой точки: tA=0, tB=π.
Применяя формулы
.gif)
Следовательно,
Ответ:
15. Вычислить работу, совершаемую силой тяжести при перемещении точки массы m по дуге АВ некоторой кривой.
Если выбрать прямоугольную систему координат так, чтобы направление оси Оz совпало с направлением силы тяжести, то действующая на точку сила
а ее проекции на оси координат Fx=P=O, Fy=Q=0, Fz=R=mg.
Искомая работа согласно формуле
Она зависит только от разности аппликат начала и конца пути, но не зависит от формы пути.
16. Найти работу силового поля, в каждой точке (х,у) которого напряжение (сила, действующая на единицу массы) , когда точка массы m описывает окружность x=accost, y=asint, двигаясь по ходу часовой стрелки.
Подставляя в формулу
проекции силы
действующей на точку: Fx=m(x+y), Fy= – mx, и преобразуя криволинейный интеграл в обыкновенный с переменной t, получим
Ответ: Е=2πma2.
Библиографический список
- Лунгу К.Н. Сборник задач по высшей математике. 1 курс – 7-е изд., – М.: Айрис-пресс, 2008.
- Лунгу К.Н. Сборник задач по высшей математике. 2 курс – 5-е изд., – М.: Айрис-пресс, 2007.
- Письменный Д.Т. Конспект лекций по высшей математике: полный курс – 7-е изд. – М.: Айрис-пресс, 2008.
Все статьи автора «Рабчук Александр Викторович»

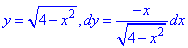
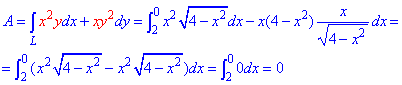
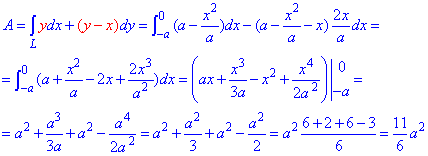
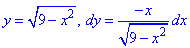
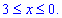
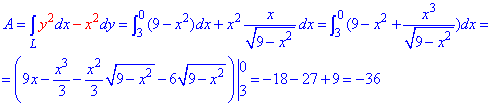
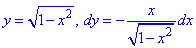
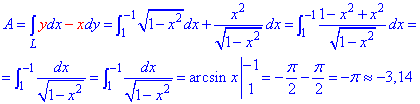





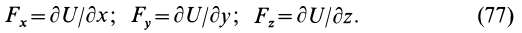
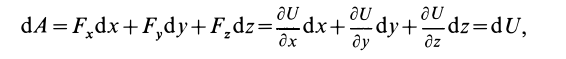

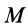
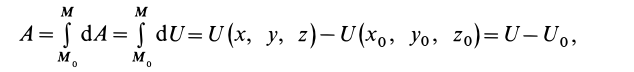

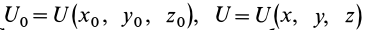
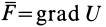
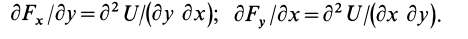
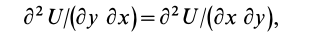
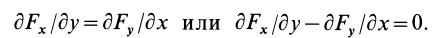
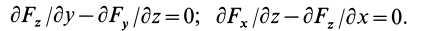
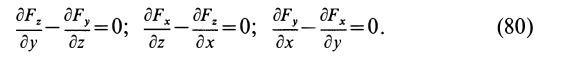
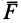
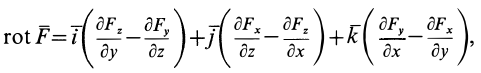

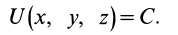
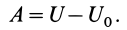
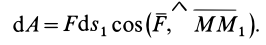
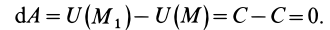
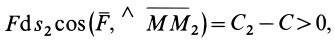
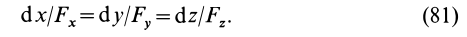
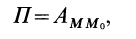
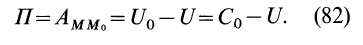
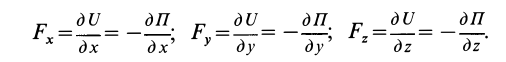
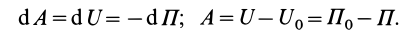

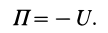
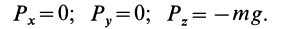
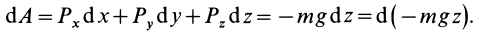
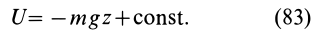
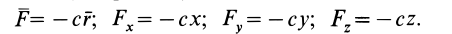
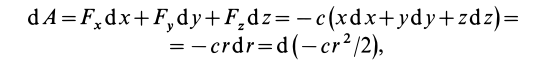
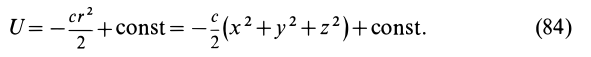
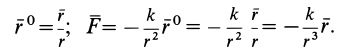
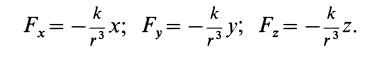
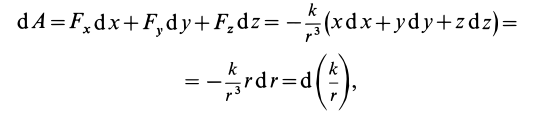
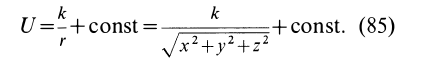
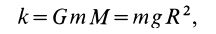
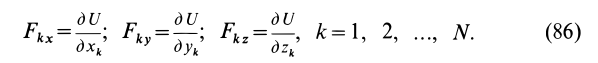
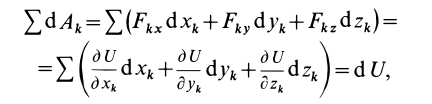

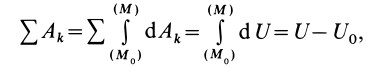

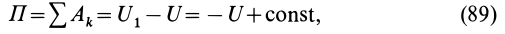
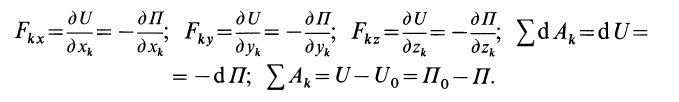
.gif)
.gif)
.gif)
.gif)
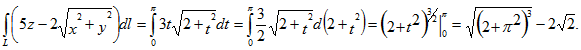
.gif)
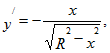
.gif)
.gif)
.gif)
.gif)
.gif)
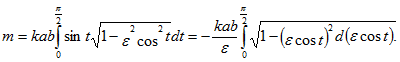
.gif)
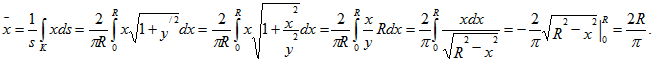
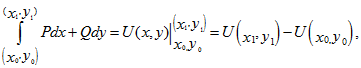
.gif)
.gif)
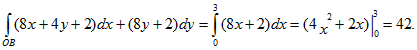
.gif)
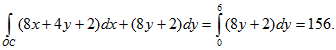
.gif)
.gif)
.gif)
.gif)
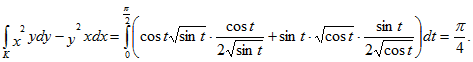
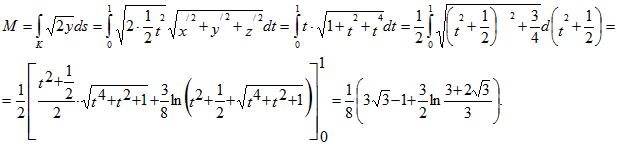
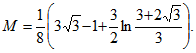
.gif)
.gif)
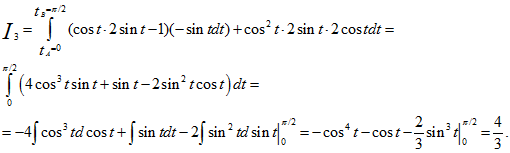
.gif)
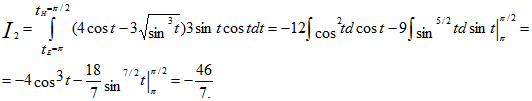
.gif)
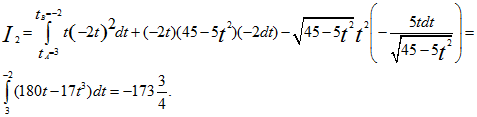
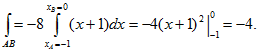
.gif)
.gif)
.gif)
.gif)
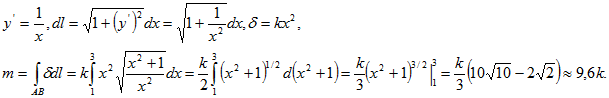
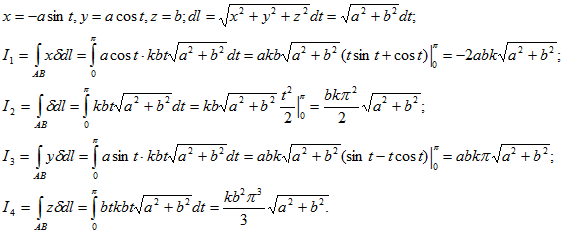
.gif)