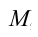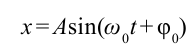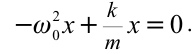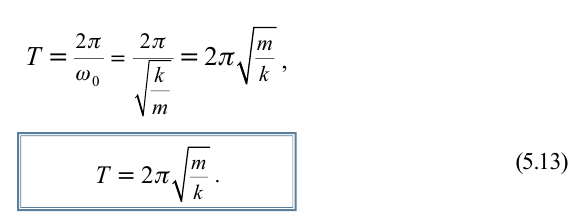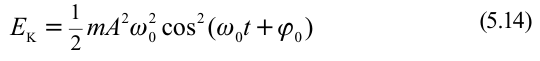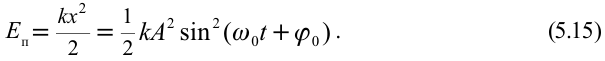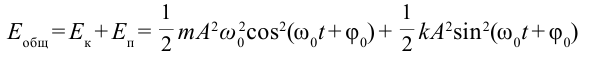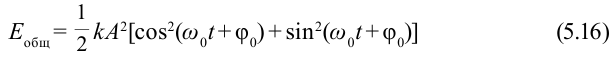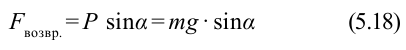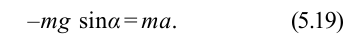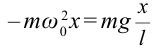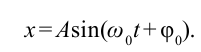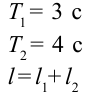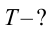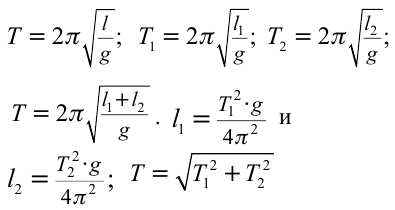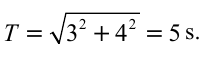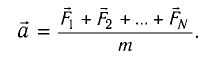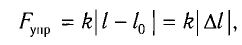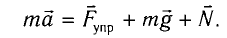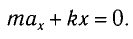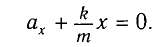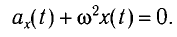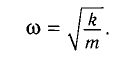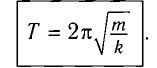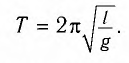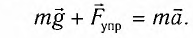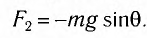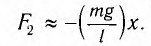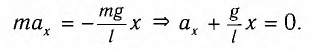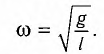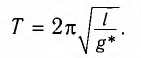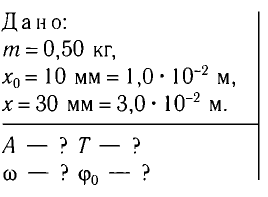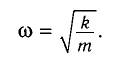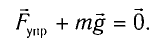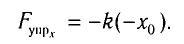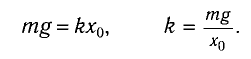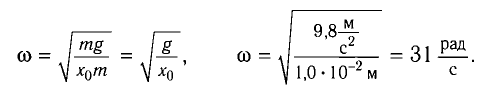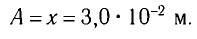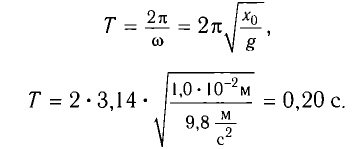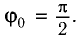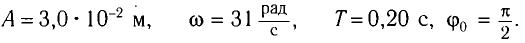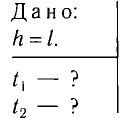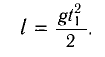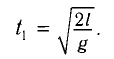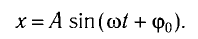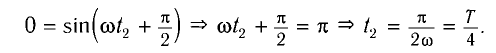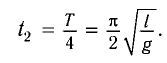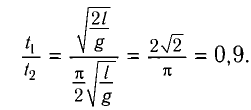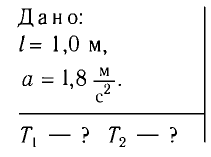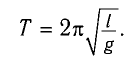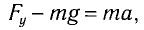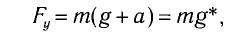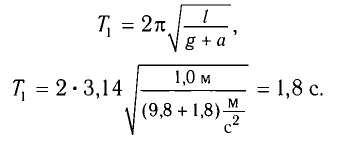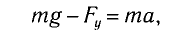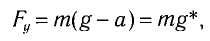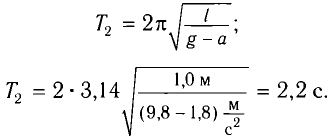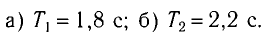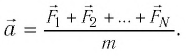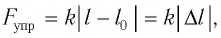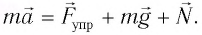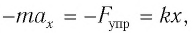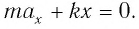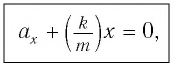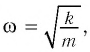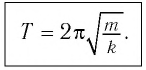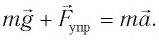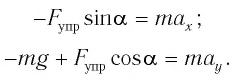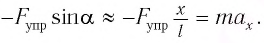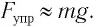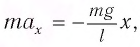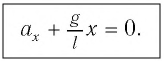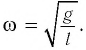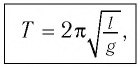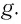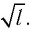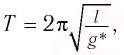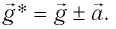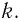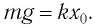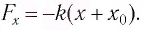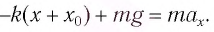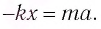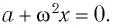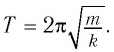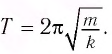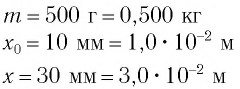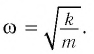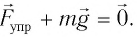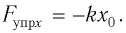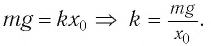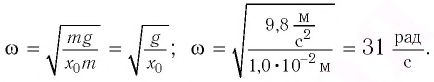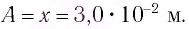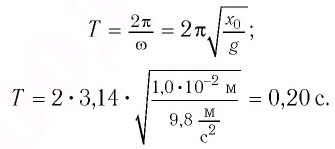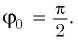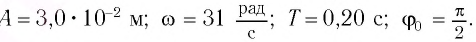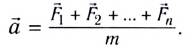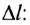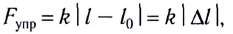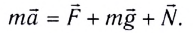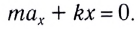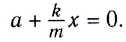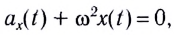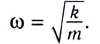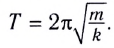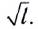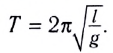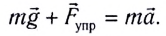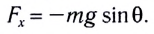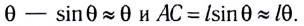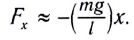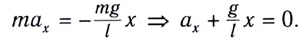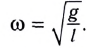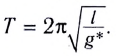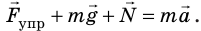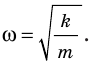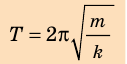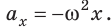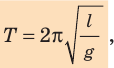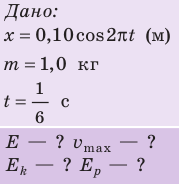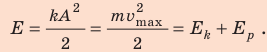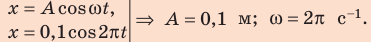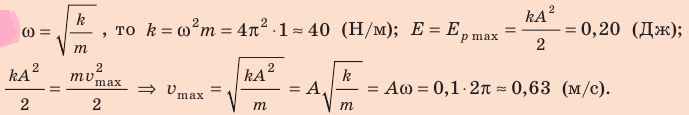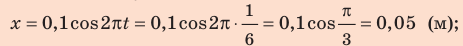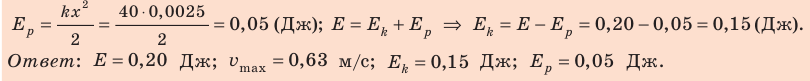Формулы математического маятника в физике
Формулы математического маятника
Определение и формулы математического маятника
Определение
Математический маятник — это колебательная система, являющаяся частным случаем физического маятника, вся масса которого
сосредоточена в одной точке, центре масс маятника.
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.
Уравнение движения математического маятника
Математический маятник — классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]
где $varphi $ — угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]
где $alpha $ — начальная фаза колебаний; ${varphi }_0$ — амплитуда колебаний; ${omega }_0$ — циклическая частота.
Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
[ {omega }_0=sqrt{frac{g}{l}}left(3right).]
Период колебаний математического маятника ($T$) в этом случае равен:
[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]
где $E_k$ — кинетическая энергия маятника; $E_p$ — потенциальная энергия маятника; $v$ — скорость движения маятника; $x$ — линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол — смещение связан с $x$ как:
[varphi =frac{x}{l}left(6right).]
Максимальное значение потенциальной энергии математического маятника равно:
[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]
Максимальная величина кинетической энергии:
[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]
где $h_m$ — максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ — максимальная скорость.
Примеры задач с решением
Пример 1
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
Решение. Сделаем рисунок.
Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
[frac{mv^2}{2}=mgh left(1.1right).]
Из уравнения (1.1) найдем искомую высоту:
[h=frac{v^2}{2g}.]
Ответ. $h=frac{v^2}{2g}$
Пример 2
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
[T=2pi sqrt{frac{l}{g}}left(2.1right).]
Выразим из нее ускорение:
[g=frac{4{pi }^2l}{T^2} .]
Проведем вычисления ускорения силы тяжести:
[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).]
Ответ. $g=9,87 frac{м}{с^2}$
Читать дальше: формулы пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Колебательное движение. Математический маятник
- Механические колебания
- Математический маятник
- Параметры колебаний математического маятника
- Задачи
- Лабораторная работа №4. Исследование колебаний математического маятника
п.1. Механические колебания
Кроме прямолинейного и криволинейного движения, с которыми мы уже познакомились, существует еще один вид механического движения – колебательный.
Механические колебания — это движения тел, которые в той или иной степени повторяются через определенные промежутки времени.
Примеры колебательных движений:
- движение маятника в часах;
- колебание автомобиля на рессорах;
- покачивание деревьев на ветру;
- раскачивание качели;
- сокращения сердца и легких;
- движение крыльев насекомых и птиц.
п.2. Математический маятник
Математическим маятником называют тело, подвешенное на длинной нерастяжимой нити, размеры которого значительно меньше длины нити.
Нить считается нерастяжимой и невесомой, а тело – материальной точкой на этой нити.
 |
В положении равновесия тело (шарик) находится внизу. Отклонение от положения равновесия называют смещением тела, обозначают буквой x и измеряют в метрах (в СИ). Наибольшее смещение маятника от положения равновесия называют амплитудой колебаний, обозначают буквой A. В проекции на горизонтальную ось OX смещение изменяется в интервале (-Aleq xleq A). В положении равновесия x=0. Если маятник после смещения в положение 1, прошел положение равновесия 2, отклонился в положение 3, опять прошел положение 2, и вернулся в положение 1, говорят, что маятник совершил полное колебание. |
п.3. Параметры колебаний математического маятника
Период колебаний математического маятника – это время, за которое маятник совершает одно полное колебание. Период колебаний равен: $$ T=2pisqrt{frac Lg} $$ где (L) – длина маятника, (g) – ускорение свободного падения.
На поверхности Земли (gapprox 9,8 м/с^2)
Частота колебаний математического маятника – это количество полных колебаний, которые маятник совершает за единицу времени: $$ f=frac 1T=frac{1}{2pi}sqrt{frac gL} $$
Период и частота колебаний – взаимно обратные величины
Период в СИ измеряют в секундах, частоту – в герцах: 1 Гц=1 c-1
Формула для периода колебаний справедлива для небольших отклонений маятника (на угол порядка 15-20° от положения равновесия).
п.4. Задачи
Задача 1. Маятник совершил 3 полных колебания за 9 с. Найдите период и частоту его колебаний. Чему равна длина нити, на которой подвешен маятник (ответ дайте в см, с округлением до целых)?
Дано:
(N=3)
(t=9 c)
__________________
(T, f, L-?)
Период колебаний: (T=frac tN)
Частота колебаний: (f=frac 1T=frac Nt)
Длина нити: $$ T=2pisqrt{frac Lg}Rightarrow sqrt{frac Lg}=frac{T}{2pi}Rightarrow frac Lg=left(frac{T}{2pi}right)^2Rightarrow L=gleft(frac{T}{2pi}right)^2 $$ Подставляем: begin{gather*} T=frac 93=3 (c)\ f=frac 13 (Гц)\ L=9,8cdotleft(frac{3}{2pi}right)^2approx 2,234 (м)approx 223 (см) end{gather*} Ответ: 3 с; 1/3 Гц; 223 см
Задача 2. Математический маятник колеблется с частотой 20?тиы кГц. Найдите период колебаний и число колебаний в минуту.
Дано:
(f=20 кГц=2cdot 10^4 Гц)
(t=1 мин=60 с)
__________________
(T, N-?)
Период колебаний: (T=frac 1f)
Частота колебаний за время (t: N=ft)
Подставляем: begin{gather*} T=frac{1}{2cdot 10^4}=0,5cdot 10^{-4} (c)=50cdot 10^{-6} (c)=50 (мкс)\ N=2cdot 10^4cdot 60=1,2cdot 10^6 end{gather*} Ответ: 50 мкс; 1,2·106
Задача 3. Расстояние от улья до цветочного поля 600 м. Пчела летит за нектаром со скоростью 8 м/с и машет крылышками с частотой 440 Гц. Возвращаясь в улей с нектаром, пчела летит со скоростью 5 м/с и машет крылышками с частотой 320 Гц. Найдите разность в количестве взмахов крылышками на пути туда и обратно.
Дано:
(s=600 м )
(v_1=8 м/с)
(f_1=440 Гц)
(v_2=5 м/с)
(f_2=320 Гц)
__________________
(triangle N-?)
Время полета из улья за нектаром (t_1=frac{s}{v_1})
Количество взмахов крылышками (N_1=f_1 t_1=f_1frac{s}{v_1})
Аналогично количество взмахов на пути назад (N_2=f_2frac{s}{v_2})
Найдем каждое из (N): begin{gather*} N_1=440cdotfrac{600}{8}=33000\ N_2=320cdotfrac{600}{5}=38400 end{gather*} На пути обратно пчела с грузом делает больше взмахов. Искомая разность: $$ triangle N=N_2-N_1=38400-33000=5400 $$ Ответ: 5400
Задача 4. Определите длину математического маятника с периодом колебаний 1с, если он находится: а) на Луне ((g_л=1,6 м/с^2)); б) на Марсе ((g_м=3,6 м/с^2)). Ответ запишите в см, с точностью до десятых.
Дано:
(T=1 с )
(g_л=1,6 м/с^2 )
(g_м=3,6 м/с^2)
__________________
(L_л, L_м-?)
Длина нити: begin{gather*} T=2pisqrt{frac Lg}Rightarrowsqrt{frac Lg} =frac{T}{2pi}Rightarrowfrac Lg=left( frac{T}{2pi}right)^2Rightarrow L = gleft(frac{T}{2pi}right)^2 end{gather*} На Луне: $$ L_л=1,6cdotleft(frac{1}{2pi}right)^2approx 0,0405 (м)approx 4,1 (см) $$ На Марсе: $$ L_м=3,6cdotleft(frac{1}{2pi}right)^2approx 0,0912 (м)approx 9,1 (см) $$ Ответ: 4,1 см; 9,1 см
п.5. Лабораторная работа №4. Исследование колебаний математического маятника
Цель работы
Исследовать, от каких величин зависит период колебаний математического маятника.
Теоретические сведения
При малых отклонениях (порядка 15-20° от вертикали) период колебаний математического маятника определяется формулой: $$ T=2pisqrt{frac Lg} $$ где (L) – длина маятника, (g) – ускорение свободного падения.
Для работы принять (gapprox 9,80665 м/с^2).
При заданном периоде колебаний для длины маятника получаем: $$ L=gleft(frac{T}{2pi}right)^2 $$
Приборы и материалы
Два лабораторных грузика по 100 г, крепкая нить (1,5-2 м), линейка (30-50 см), штатив, секундомер.
Ход работы
1. Рассчитайте длину нитей, необходимых для создания маятников с периодами колебаний (T_1=1 с; T_2=2 с).
2. Закрепите один грузик на нити и подвесьте его на штативе так, чтобы длина подвеса была равна расчетной длине (L_1).
3. Отклоните грузик на небольшой угол, отпустите его и с помощью секундомера измерьте время, за которое маятник совершит 10 полных колебаний. Повторите опыт 5 раз. Проведите расчеты для определения периода колебаний (T_{1 эксп}) по методике, изложенной в лабораторной работе №2 (см. §4 данного справочника).
4. Теперь подвесьте грузик так, чтобы длина подвеса была равна расчетной длине (L_2). Повторите серию из 5 экспериментов и определите (T_{2 эксп}).
5. При длине подвеса (L_2) подвесьте к первому грузику второй. Повторите серию из 5 экспериментов и определите (T ‘). Сравните (T ‘) и (T_{2 эксп}).
6. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Расчет длины нитей begin{gather*} L=gleft(frac{T}{2pi}right)^2\ T_1=1 c, L_1=9,80665cdotleft(frac{1}{2pi}right)^2approx 0,248 (м)=24,8 (см)\ T_2=2 c, L_1=9,80665cdotleft(frac{2}{2pi}right)^2approx 0,9994 (м)=99,4 (см) end{gather*}
Определение (T_{1 эксп})
Инструментальная погрешность секундомера (d=frac{triangle}{2}=0,1 c)
Время 10 колебаний
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t, c) | 9,7 | 10,2 | 9,8 | 9,9 | 10,3 | 50 |
| (triangle c) | 0,3 | 0,2 | 0,2 | 0,1 | 0,3 | 1 |
begin{gather*} t_{cp}=frac{50}{5}=10\ triangle_{cp}=frac 15=0,2 end{gather*} Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,2right}=0,2 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(10,0pm 0,2) c end{gather*} Период колебаний в 10 раз меньше: $$ T_{1 эксп}=frac{1}{10}(t_0pmtriangle t), T_{1 эксп}=(1,00pm 0,02) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T_{1 эксп}}cdot 100text{%}=frac{0,02}{1}cdot 100text{%}=2,0text{%} $$
Определение (T_{2 эксп})
Время 10 колебаний
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t, c) | 19,7 | 20,1 | 19,8 | 20,2 | 19,7 | 99,5 |
| (triangle c) | 0,2 | 0,2 | 0,1 | 0,3 | 0,2 | 1 |
begin{gather*} t_{cp}=frac{99,5}{5}=19,9\ triangle_{cp}=frac 15=0,2 end{gather*} Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,2right}=0,2 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(19,9pm 0,2) c end{gather*} Период колебаний в 10 раз меньше: $$ T_{2 эксп}=frac{1}{10}(t_0pmtriangle t), T_{2 эксп}=(1,99pm 0,02) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T_{2 эксп}}cdot 100text{%}=frac{0,02}{1,99}cdot 100text{%}approx 1,0text{%} $$
Определение (T ‘) (с двумя грузиками)
Время 10 колебаний
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t, c) | 20,2 | 19,7 | 19,6 | 20,0 | 20,3 | 99,8 |
| (triangle c) | 0,24 | 0,26 | 0,36 | 0,04 | 0,34 | 1,24 |
begin{gather*} t_{cp}=frac{99,8}{5}=19,96\ triangle_{cp}=frac{1,24}{5}approx 0,25 end{gather*} Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,25right}=0,25 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(19,96pm 0,25) c end{gather*} Период колебаний в 10 раз меньше: $$ T’=frac{1}{10}(t_0pmtriangle t), T’=(1,996pm 0,025) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T’}cdot 100text{%}=frac{0,025}{1,996}cdot 100text{%}approx 1,3text{%} $$
Полученные на опыте интервалы для (T_{2 эксп}) и (T’) (одинаковая длина нити (L_2) и разные массы грузиков – 100 г и 200 г соответственно): begin{gather*} 1,97leq T_{2 эксп}leq 2,01\ 1,971leq T’leq 2,021 end{gather*} Таким образом, (T_{2 эксп}approx T’), т.е. период колебаний математического маятника не зависит от массы груза.
Выводы
На основании проделанной работы можно сделать следующие выводы.
В работе с помощью расчетной формулы были определены длины нитей подвеса для маятников с периодами колебаний (T_1=1 с; T_2=2 с).
Полученный на опыте период колебаний для подвеса с (L_1=24,8 см) с грузиком 100 г равен $$ T_{1 эксп}=(1,00pm 0,02) c, delta=2,0text{%} $$ Полученный на опыте период колебаний для подвеса с (L_2=99,4 см) с грузиком 100 г равен $$ T_{2 эксп}=(1,99pm 0,02) c, delta=1,0text{%} $$ Полученный на опыте период колебаний для подвеса с (L_2=99,4 см) с грузиком 200 г равен $$ T’=(1,996pm 0,025) c, delta=1,3text{%} $$ Формула (T=2pisqrt{frac Lg}) данными экспериментами подтверждена.
Период колебаний математического маятника зависит от длины подвеса и не зависит от массы грузика на подвесе.
Содержание:
Пружинные и математические маятники:
Тело или система тел, совершающие периодические колебательные движения, называются маятниками. Большинство колебательных движений, встречающихся в природе, напоминают движение пружинных и математических маятников.
Система, состоящая из груза массой
Если немножко растянуть пружину и отпустить, то груз придет в колебательное движение в вертикальном направлении.
С помощью опытов мы определили, что смещение груза в зависимости от времени изменяется следующbм образом:
Если учесть, что ускорение тела, совершающего гармонические колебания 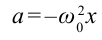
Из этого уравнения мы имеем:
Значит, частота циклического колебания тела, совершающего гармоническое колебание, зависит от параметров тел, входящих в систему колебания. Формула (5.12) называется формулой для
определения циклической (периодической) частоты пружинного маятника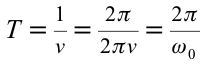
Период колебания пружинного маятника прямо пропорционален выведенному из-под квадратного корня значению массы груза и обратно пропорционален выведенному из-под квадратного корня значению упругости пружины.
Рассмотрим обмен энергиями в пружинном маятнике. Кинетическая энергия маятника, если не учитывать массу пружины, равна кинетической энергии груза, 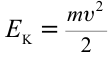
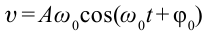
Потенциальная энергия пружинного маятника равна энергии деформации пружины, т.е.:
В большинстве случаев важно знать полную энергию системы:
Если учесть, что 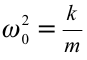
Обратите внимание, что полная энергия пружинного маятника является постоянной величиной, не зависящей от времени, т.е. соблюдается выполнение закона сохранения механической энергии.
Материальная точка, подвешенная на нерастяжимой и невесомой нити и совершающая периодическое колебательное движение вокруг равновесного состояния, называется математическим маятником.
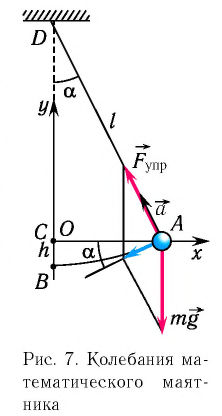
Когда маятник находится в устойчивом равновесном состоянии, вес материальной точки 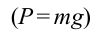

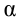
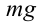

Из рис. 5.4. видим, что:
Согласно второму закону Ньютона, сила 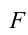
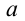
Из-за того, что угол наклона очень маленький 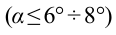
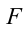
Если смещение материальной точки (шарика) во время колебательного процесса отметить буквой 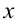
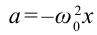
Следовательно
Исходя из смысла периода колебания и учитывая, что 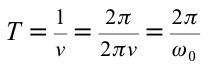
Эта формула, определяющая период колебания математического маятника, называется формулой Гюйгенса. Отсюда вытекают следующие законы математического маятника:
- при маленьких углах наклона (а) математического маятника, его период колебания не зависит от амплитуды колебания.
- период колебания математического маятника также не зависит от массы подвешенного на него груза;
- период колебания математического маятника прямо пропорционален выведенному из-под квадратного корня значению длины маятника и обратно пропорционален выведенному из-под квадратного корня значению ускорения свободного падения.
Отсюда колебание математического маятника записывается следующим выражением:
Следует отметить, что когда амплитуда колебания или угол наклона велики, колебания математического маятника не являются гармоническим. В этом случае нельзя считать 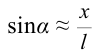
Пример:
Период колебания первого маятника равен 3 сек, второго – 4 сек. Найдите период колебания маятника с длиной, равной сумме длин этих маятников.
Дано:
Найти:
Формула:
Решение:
Ответ: 5 cек.
Пружинный и математический маятники
Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:
Закон Гука: модуль силы упругости 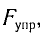
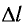
где k — жесткость тела, 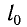
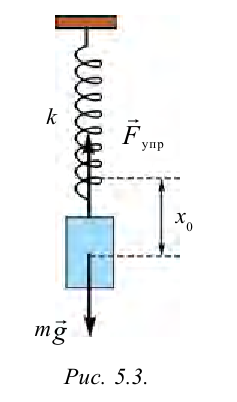
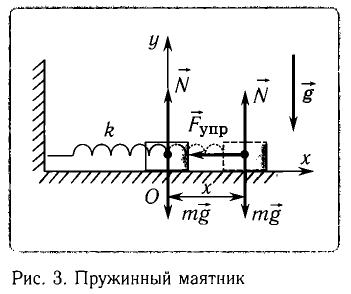
Рассмотрим пружинный маятник, представляющий собой колебательную систему, образованную грузом на пружине.
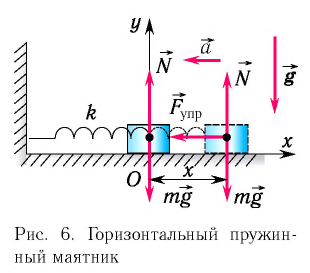
Пусть груз массой т, лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу невесомой пружины жесткостью k (рис. 3). Второй конец пружины закреплен относительно данной инерциальной системы отсчета (ИСО).
Выведем груз из положения равновесия, сместив его на расстояние х вправо. В пружине возникнет сила упругости 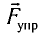
Запишем второй закон Ньютона для движения груза:
В проекции на ось Ох действующих на груз сил с учетом закона Гука получаем
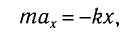
Следовательно,
Это уравнение аналогично уравнению гармонических колебаний
Сравнивая эти два уравнения, находим циклическую частоту колебаний пружинного маятника:
Тогда период колебаний пружинного маятника можно найти по формуле
Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды его колебаний (в пределах выполнимости закона Гука).
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греческих слов 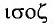
Изохронность колебаний маятника была открыта Галилео Галилеем в 1583 г. при изучении движения грузика, подвешенного на нити. Моделью данной колебательной системы является математический маятник.
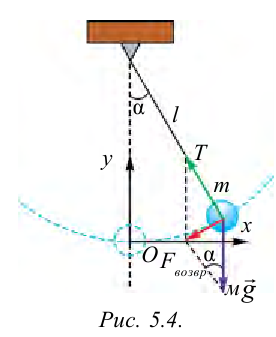
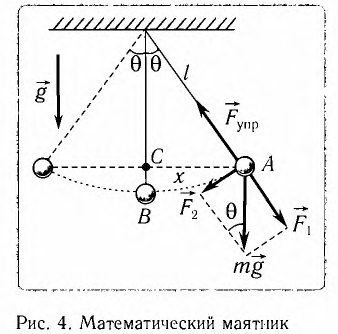
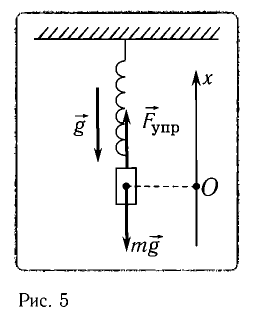
Математическим маятником называется материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 4).
Математический маятник — это идеализированная модель реального маятника при условии, что длина нити намного больше размеров подвешенного на ней тела и масса нити намного меньше массы тела. Кроме того, деформацией нити можно пренебречь.
Галилео Галилей экспериментально определил, что период малых колебаний (9 < 10°) математического маятника в поле силы тяжести не зависит от его массы и амплитуды колебаний (угла начального отклонения 
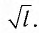
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса:
При углах отклонения математического маятника 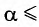
Отклонение маятника от положения равновесия будем характеризовать углом 
Согласно второму закону Ньютона для движения шарика можем записать:
Смещение маятника вдоль дуги х = l

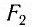
Заметим, что при малых углах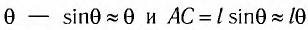
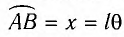
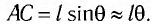


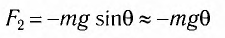
является очень хорошим приближением.
Подставляя в выражение (1) значение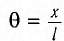
Таким образом, уравнение движения маятника запишется в виде
Поскольку полученное уравнение совпадает с уравнением гармонических колебаний 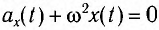
Как видно из этой формулы, циклическая частота не зависит от массы маятника и амплитуды его колебаний, а определяется только его длиной и ускорением свободного падения.
В общем случае, когда маятник находится в однородных полях нескольких сил, для определения периода колебаний следует ввести «эффективное ускорение» 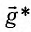
Пример:
Определите амплитуду А, циклическую частоту 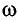
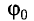
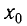
Решение
Циклическая частота колебаний «вертикального» пружинного маятника также определяется по формуле
Найдем жесткость k пружины. Из условия равновесия тела следует
По закону Гука
В проекции на ось Ох условие равновесия запишется в виде:
Отсюда для циклической частоты 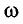
Так как по условию задачи тело сместили на расстояние х = 30 мм от положения равновесия, то амплитуда его колебаний
Период колебаний находим из соотношения
Поскольку в начальный момент времени тело было смещено на максимальную величину, то начальная фаза колебаний
Ответ:
Пример:
Металлический шарик, подвешенный на длинной легкой нерастяжимой нити, поднимают по вертикали до точки подвеса и отпускают. Затем нить маятника отклоняют на небольшой угол от вертикали и также отпускают. В каком из этих случаев шарик быстрее возвратится в начальное положение?
Решение
В первом случае шарик свободно падает без начальной скорости с высоты h = l, следовательно,
Отсюда находим промежуток времени 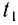
Во втором случае промежуток времени 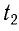
Поскольку в начальный момент времени t = 0 маятник имеет максимальное
отклонение от положения равновесия, то начальная фаза колебаний 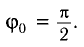
Используя формулу для периода колебаний математического маятника
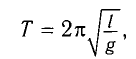
Разделив почленно уравнения для промежутков времени 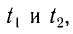
Ответ: шарик быстрее возвратится в начальное положение в случае, когда он движется вертикально вниз.
Пример:
Найдите периоды колебаний математического маятника длиной l= 1,0 м при перемещении его точки подвеса с ускорением, модуль которого а = 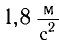
Решение
Период колебаний математического маятника в поле силы тяжести Земли
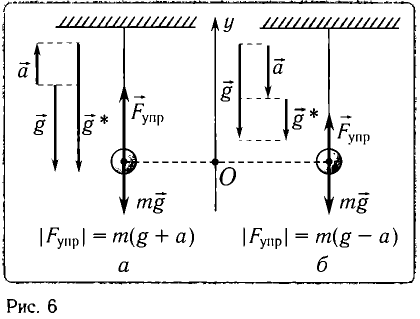
а) При движении маятника с ускорением 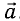
где Fy — проекция силы упругости нити.
Откуда находим
где g* = g + а — «эффективное ускорение».
Период колебаний определяется по формуле
б) При движении точки подвеса маятника с ускорением 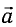
где Fy — проекция силы упругости нити. Откуда находим
где g*=g-a — «эффективное ускорение». Период колебаний
Ответ:
Что такое пружинный и математический маятники
Второй закон Ньютона (основной закон динамики): ускорение тела прямо пропорционально результирующей силе и обратно пропорционально массе тела:
Закон Гука: при упругих деформациях сжатия и растяжения модуль силы упругости прямо пропорционален модулю изменения длины тела:
где 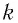
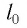
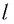
Колебательная система, состоящая из тела с прикрепленной к нему пружиной, называется пружинным маятником. Пружина может располагаться как вертикально (вертикальный пружинный маятник), так и горизонтально (горизонтальный пружинный маятник).
Рассмотрим колебания горизонтального пружинного маятника. Пусть груз массой 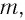
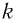
Выведем груз из положения равновесия, сместив его на расстояние 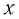
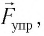
Согласно второму закону Ньютона для движения груза
В проекции на ось 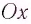
или
Перепишем полученное соотношение в виде:
которое является уравнением гармонических колебаний пружинного маятника.
Сравнивая (1) с уравнением гармонических колебаний 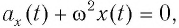
которая определяется массой 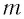
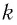
Для нахождения периода колебаний пружинного маятника воспользуемся формулой 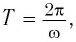
Как следует из формул (2) и (3), период и частота колебаний пружинного маятника не зависят от амплитуды его колебаний (в пределах выполнимости закона Гука).
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греч. 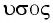
Изохронность колебаний маятника была открыта Гали-лео Галилеем в 1583 г. при изучении движения груза, подвешенного на нити. Моделью данной колебательной системы является математический маятник.
Колебательная система, состоящая из находящегося в поле силы тяжести тела, подвешенного на легкой нерастяжимой нити, размеры которого малы по сравнению с длиной нити, а его масса значительно больше массы нити, называется математическим маятником. При таких условиях тело можно считать материальной точкой, а нить — легкой нерастяжимой (рис. 7).
Рассмотрим колебания математического маятника.
Отклонение маятника от положения равновесия будем характеризовать углом 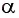
После отклонения маятника на него действуют две силы: направленная вертикально вниз сила тяжести 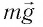
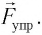
Согласно второму закону Ньютона для движения маятника можем записать:
В проекциях на выбранные оси координат 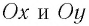
Для углов отклонения 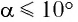
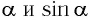
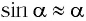
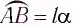
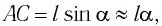
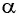
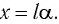
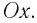
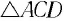
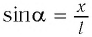
Таким образом, силой, возвращающей маятник к устойчивому положению равновесия, является сила упругости его нити.
При малых углах отклонения маятника проекция вектора ускорения 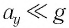
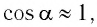
Следовательно, уравнение движения маятника вдоль оси 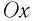
где 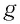
Отсюда получаем уравнение гармонических колебаний математического маятника:
При сравнении уравнения (8) с уравнением гармонических колебаний 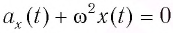
Тогда период малых колебаний математического маятника в поле тяжести Земли определяется по формуле Гюйгенса:
которую впервые получил ученик И. Ньютона Христиан Гюйгенс.
При углах отклонения математического маятника 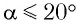
Как видно из формул (9) и (10), циклическая частота и период математического маятника не зависят от массы маятника и амплитуды его колебаний, а определяются только его длиной 
Галилео Галилей первый экспериментально определил, что период малых колебаний 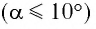
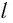
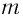
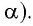
Если маятник приобретает дополнительное ускорение 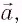
где 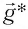
- Заказать решение задач по физике
Пример:
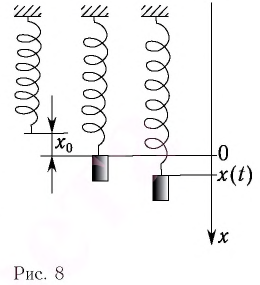
Выведите формулу для периода колебаний вертикального пружинного маятника, если масса груза 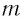
Решение
Рассмотрим вертикальное движение груза, происходящее под действием силы упругости пружины и силы тяжести груза после толчка. Начало координат поместим в точку, соответствующую равновесному положению тела (рис. 8). В этом положении пружина растянута на величину 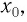
При смещении груза на величину 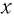
Тогда по второму закону Ньютона
С учетом соотношения (1) это уравнение перепишем в виде:
Если ввести обозначение 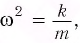
Оно описывает гармонические колебания вертикального пружинного маятника с частотой такой же, как у горизонтального пружинного маятника. Следовательно, период колебаний вертикального пружинного маятника такой же, как и горизонтального:
Ответ:
Таким образом, действующая в колебательной системе постоянная сила только смещает положения равновесия, но не изменяет частоту колебаний.
Пример:
Определите амплитуду 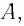
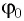
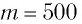
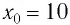
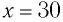
Дано:
Решение
Циклическая частота колебаний вертикального пружинного маятника так же, как и горизонтального, определяется по формуле (см. пример 1):
Для нахождения жесткости к пружины запишем условие равновесия тела:
По закону Гука
В проекции на ось 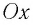
Отсюда для циклической частоты 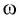
Амплитуда колебаний маятника определяется начальным смешением:
Период колебаний находим из соотношения:
Поскольку в начальный момент времени тело было смещено на максимальную величину, то начальная фаза колебаний
Ответ:
Подробное объяснение пружинного и математического маятника
Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:
Закон Гука: модуль силы упругости 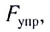
где k — жесткость тела, 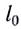
Простейшая колебательная система может быть получена с использованием груза и пружины.
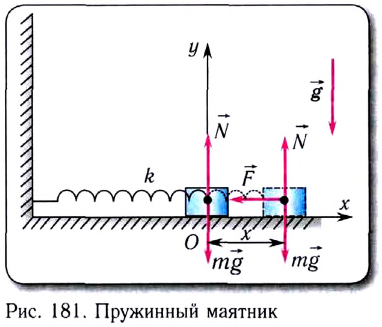
Прикрепим груз массой m, лежащий на гладкой горизонтальной поверхности, к невесомой упругой пружине жесткостью k, второй конец которой зафиксирован (рис. 181). Такая система называется пружинным маятником.
Запишем второй закон Ньютона для этой системы
В проекции на ось Ох с учетом закона Гука получаем
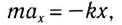
Запишем это уравнение в форме, аналогичной уравнению движения гармонического осциллятора:
Сравнивая полученное выражение с уравнением гармонических колебаний
находим циклическую частоту колебаний пружинного маятника
Тогда период колебаний пружинного маятника можно найти по формуле
Свойство независимости периода колебаний маятника от амплитуды, открытое Галилеем, называется изохронностью (от греческих слов 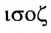
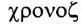
Как видим, пружинный маятник обладает свойством изохронности, поскольку период его колебаний не зависит от амплитуды.
Одной из наиболее распространенных колебательных систем является математический маятник.
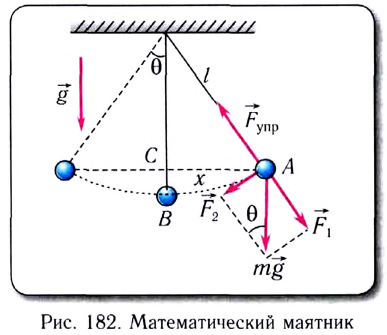
Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 182).
Галилео Галилей экспериментально установил, что период колебаний математического маятника в поле силы тяжести не зависит от его массы и амплитуды колебаний (угла начального отклонения). Он установил также, что период колебаний прямо пропорционален
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса:
При углах отклонения математического маятника 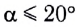
Отклонение маятника от положения равновесия будем характеризовать углом 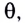
Из второго закона Ньютона следует (см. рис. 182):
Смещение маятника вдоль дуги 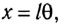
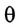
Возвращающей силой в данном случае является проекция на касательную к дуге силы тяжести 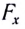
Заметим, что при малых углах 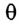
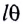
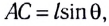
Для небольших углов (до 10°) значения 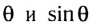
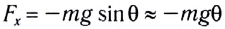
Используя полученное соотношение между координатой х и углом 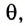
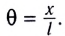
Таким образом, уравнение движения маятника запишется в виде
Поскольку полученное уравнение совпадает с уравнением гармонических колебаний 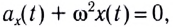
Как видно из этой формулы, циклическая частота не зависит от массы маятника и амплитуды его колебаний, а определяется только его длиной и ускорением свободного падения.
В общем случае, когда маятник находится в однородных полях нескольких сил, для определения периода колебаний следует ввести «эффективное ускорение» 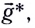
Математический и пружинный маятники и энергия колебаний
Колебательные движения очень разнообразны. При этом существует «классика» колебательных движений — они описаны сотни лет назад, их изучением занимались Галилео Галилей (1564– 1642) и Христиан Гюйгенс (1629–1695). Это колебания пружинного и математического маятников.
Колебания пружинного маятника
Пружинный маятник — это колебательная система, представляющая собой закрепленное на пружине тело.
Рассмотрим колебания горизонтального пружинного маятника — тележки массой m, закрепленной на пружине жесткостью k. Будем считать, что силы трения, действующие в системе, пренебрежимо малы, а значит, колебания маятника незатухающие (их амплитуда с течением времени не изменяется, а полная механическая энергия системы сохраняется). При этом потенциальная энергия деформированной пружины будет превращаться в кинетическую энергию движения тележки, и наоборот.
Колебания пружинного маятника:
Обратите внимание! В течение всего времени колебания сила упругости направлена в сторону, противоположную смещению тележки, — сила упругости все время «толкает» тележку к положению равновесия.
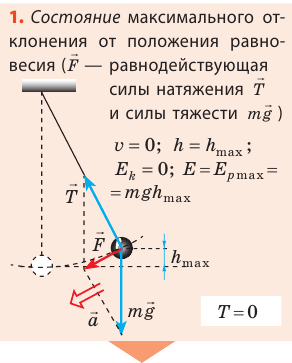
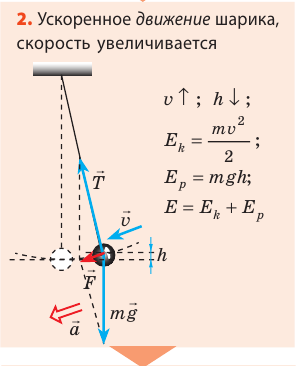
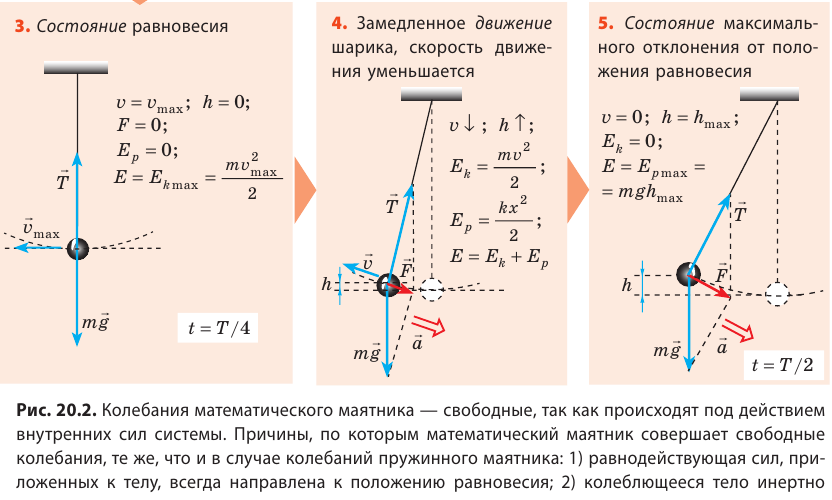
Итак, причины свободных колебаний пружинного маятника: 1) действующая на тело сила всегда направлена к положению равновесия; 2) колеблющееся тело инертно, поэтому оно не останавливается в положении равновесия (когда равнодействующая сил становится равной нулю), а продолжает движение в том же направлении.
Как вычислить период колебаний пружинного маятника
Рассмотрим колебания тележки, закрепленной на горизонтальной пружине, с точки зрения второго закона Ньютона (рис. 20.1). Запишем уравнение второго закона Ньютона в векторном виде:
Сила тяжести и сила нормальной реакции опоры уравновешивают друг друга, поэтому 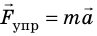
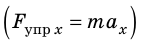
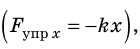
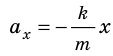
Последнее уравнение можно записать в виде 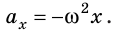
Приняв во внимание, что 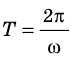
Обратите внимание! Период колебаний пружинного маятника не зависит ни от амплитуды колебаний, ни от места расположения маятника (на поверхности Земли или Луны, в космическом корабле и т. д.), — он определяется только характеристиками самой колебательной системы «тело — пружина». Если период Т колебаний тела и жесткость k пружины известны, можно найти массу m тела. Такой способ определения массы используют в состоянии невесомости, когда обычные весы не работают.
Что называют математическим маятником
Любое твердое тело, которое совершает или может совершать колебания относительно оси, проходящей через точку подвеса, называют физическим маятником. Примером может быть игрушка, подвешенная на нити в салоне автомобиля. Если игрушку вывести из положения равновесия, она начнет колебаться. Однако изучать такие колебания сложно: их характер определяется размерами и формой игрушки, свойствами нити и другими факторами.
Чтобы размеры тела не влияли на характер его колебаний, следует взять нить, длина которой намного больше размеров тела, а масса незначительна по сравнению с его массой. В таком случае тело можно считать материальной точкой. А чтобы во время колебаний тело все время находилось на одинаковом расстоянии от точки подвеса, нить должна быть нерастяжимой. Таким образом будет получена физическая модель — математический маятник.
Математический маятник — это физическая модель колебательной системы, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити, и гравитационного поля.
Колебания математического маятника
Возьмем небольшой, но достаточно тяжелый шарик и подвесим его на длинной нерастяжимой нити — такой маятник можно считать математическим. Если отклонить шарик от положения равновесия и отпустить, то в результате действия гравитационного поля Земли (силы тяжести) и силы натяжения нити шарик начнет колебаться около положения равновесия. Поскольку сопротивление воздуха пренебрежимо мало, а силы, действующие в системе, являются консервативными, полная механическая энергия шарика будет сохраняться: потенциальная энергия шарика будет превращаться в его кинетическую энергию, и наоборот.
Рассмотрите колебательное движение шарика (рис. 20.2). Объясните причины его движения. Какие происходят превращения энергии?
Как вычислить период колебаний математического маятника
Математический маятник, отклоненный от положения равновесия на небольшой угол (3–5°), будет совершать гармонические колебания, то есть ускорение его движения все время будет прямо пропорционально смещению и направлено в сторону, противоположную смещению:
Для математического маятника: 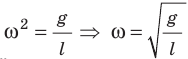
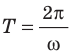
где l — длина маятника; g — ускорение свободного падения.
Данную формулу впервые получил в XVII в. голландский ученый Христиан Гюйгенс, поэтому ее называют формулой Гюйгенса.
Период колебаний математического маятника не зависит от массы маятника, а определяется только длиной нити и ускорением свободного падения в том месте, где расположен маятник. Поэтому, измерив длину нити и период колебаний маятника, можно определить ускорение свободного падения в данной местности.
Пример:
Уравнение колебаний груза массой 1 кг на пружине имеет вид: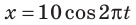
Решение:
Трение отсутствует, поэтому полная механическая энергия сохраняется:
Сравним уравнение колебаний в общем виде с уравнением, приведенным в задаче:
Поскольку
Определив удлинение пружины через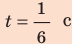
Выводы:
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
- Путь и перемещение
- Равномерное прямолинейное движение
- Вращательное движение тела
- Равномерное движение материальной точки по окружности
- Колебательное движение
- Физический и математический маятники
Содержание
- Математический маятник
- Определение
- Колебания
- Свойства
- Период
- Практическое применение
- Видео
- Математический маятник — определение, формулы и принцип действия
- Простая гравитация
- Крутящий момент
- Сохранение механической энергии
- Колебательные движения
- Составной маятник
- Историческая хроника
- Исследования Галилея
- Маятниковые часы
Математический маятник
Содержание:
Определение
Представьте себе некую механическую систему, которая состоит из некой материальной точки (тела), которая висит на нерастяжимой невесомой нити (при этом масса нити ничтожно мала по сравнению с массой тела). Вот такая механическая система и является маятником или осциллятором, как его еще называют. Впрочем, могут быть и другие виды такого устройства. Чем же математический маятник, осциллятор интересен для нас? Дело в том, что с его помощью можно проникнуть в суть многих интересных природных явлений в физике.
Колебания
Формула периода колебания математического маятника впервые была открыта голландским ученым Гюйгенсом в далеком XVII веке. Будучи современником Исаака Ньютона, Гюйгенс был очень увлечен такими вот маятниками, увлечен настолько, что даже изобрел специальные часы с маятниковым механизмам, и часы эти были одними из самых точных для того времени.
Маятниковые часы Гюйгенса.
Появление подобного изобретения сослужило большую пользу физике, особенно в сфере физических экспериментов, где точное измерение времени является весьма важным фактором.
Но вернемся к маятнику, итак, в основе работы маятника лежат его колебания, которые можно выразить формулой, точнее следующим дифференциальным уравнением:
Где х (t) – неизвестная функция (это угол отклонения от нижнего положения равновесия в момент t, выраженный в радианах); w – положительная константа, которая определяется из параметров маятника (w = √ g/L, где g – это ускорение свободного падения, а L – длина математического маятника (подвес).
Помимо, собственно колебаний маятник может пребывать и в положении равновесия, при этом сила тяжести, действующая на него, будет уравновешиваться силой натяжения нити. Обычный плоский маятник, пребывающий на нерастяжимой нити, является системой с двумя степенями свободы. Но если, к примеру, нитку заменить на стержень, тогда наш маятник станет системой лишь с одной степенью свободы, так как его движения будут двухмерными, а не трехмерными.
Но если же наш маятник все-таки пребывает на нити и при этом совершает интенсивные колебания вверх-вниз, тогда механическая система приобретает устойчивое положение, именуемое «верх тормашками», еще ее называют маятником Капицы.
Свойства
У маятника есть ряд интересных свойств, подтвержденных физическими законами. Так период колебаний всякого маятника зависит от таких факторов, как его размер, форма тела, расстояние между центром тяжести и точкой подвеса. Поэтому определение периода маятника является не простой задачей. А вот период математического маятника можно рассчитать точно по формуле, которая будет приведена ниже.
В ходе наблюдений за маятниками были выведены следующие закономерности:
- Если к маятнику подвешивать разные грузы с разным весом, но при этом сохранять одинаковую длину маятника, то период его колебания будет одинаковым вне зависимости от массы груза.
- Если при запуске колебаний отклонить маятник на не очень большие, но все же разные углы, то он станет колебаться в одинаковым период, но по разным амплитудам. Следовательно, период колебания у подобного маятника не зависит от амплитуды колебания, такое явление было названо изохронизмом, что с древнегреческого можно перевести как «хронос» – время, «изо» – равный, то есть «равновременный».
Период
Период маятника – показатель, который представляет период собственно колебаний маятника, их длительность. Формулу периода математического маятника можно записать следующим образом.
Где L – длина нити математического маятника, g – ускорение свободного падения, а π – число Пи, математическая константа.
Период малых колебания математического маятника никак не зависит от массы маятника и амплитуды колебания, в этой ситуации он двигается как математический маятник с заданной длинной.
Практическое применение
Вот мы добрались и до самого интересного, зачем нужен математический маятник и какое его применение на практике в жизни. В первую очередь ускорение математического маятника используется для геологоразведки, с его помощью ищут полезные ископаемые. Как это происходит? Дело в том, что ускорение свободного падения изменяется с географической широтой, так как плотность коры в разных местах нашей планеты далеко не одинакова и там где залегают породы с большей плотностью, ускорение будет немножко больше. А значит, просто подсчитав количество колебаний маятника можно отыскать в недрах Земли руду или каменный уголь, так как они имеют большую плотность, нежели другие рыхлые горные породы.
Также математическим маятником пользовались многие выдающиеся ученые прошлого, начиная с античности, в частности Архимед, Аристотель, Платон, Плутарх. Так Архимед и вовсе использовал математический маятник во всех своих вычислениях, а некоторые люди даже верили, что маятник может влиять на судьбы людей и пытались делать с его помощью предсказания будущего.
Видео
И в завершение образовательное видео по теме нашей статьи.
Источник
Математический маятник — определение, формулы и принцип действия
Если какую-нибудь материальную точку подвесить на нить, почти не имеющей веса, то получится математический маятник Он свободно качается взад и вперёд под действием силы тяжести, которая возвращает подвешенное тело в положение равновесия, если его сместить. Математика здесь довольно сложная. Первые научные исследования в этой области принадлежат Галилео Галилею, именно они легли в основу самой точной технологии хронометража.
Простая гравитация
Так называемый простой маятник — это всего лишь идеализированная математическая модель. Это груз на конце безмассового шнура, подвешенного на оси без трения. Если его толкнуть, он будет раскачиваться с постоянной амплитудой, но с некоторыми условиями:
Дифференциальное уравнение, которое представляет движение простого маятника, выглядит следующим образом (где g — ускорение силы тяжести, ℓ — длина маятника, θ — угловое смещение): d² / dt² + g / ℓ sin θ = 0.
На графике 1 показаны силы, действующие на отвес. Стоит обратить внимание, что груз описывает дугу. Угол θ измеряется в радианах, и это имеет решающее значение для этой формулы. Синяя стрелка — гравитационная сила, которая действует на маятник, а фиолетовые векторы — это та же самая сила, только разложенная на компоненты, параллельные и перпендикулярные мгновенному движению груза.
Направление мгновенной скорости всегда указывается вдоль красной оси, которая считается тангенциальной, поскольку её направление всегда касается окружности. И прежде чем вывести уравнение силы деривации, стоит вспомнить второй закон Ньютона: F = ma. За F принимают сумму сил, действующих на объект, m — масса, a — ускорение.
Поскольку интерес составляет только измерение скорости, а груз вынужден оставаться на круговой траектории, уравнение Ньютона применяется только к тангенциальной оси. Короткая фиолетовая стрелка представляет компонент гравитационной силы, используя тригонометрию можно определить её величину. Таким образом, получается (g — ускорение силы тяжести вблизи поверхности земли): F = — mg sin θ = ma; a = — g sin θ.
Отрицательный знак на правой стороне означает, что θ и отвес всегда указываются в противоположных направлениях. Это вполне логично, поскольку когда маятник качается сильнее влево, ожидается, что он ускорится при движении назад — вправо. Это линейное ускорение, a вдоль красной оси может быть связано с изменением угла θ по формулам длины дуги (s): s = ℓθ; v = ds / dt = ℓdθ / dt; a = d²s / dt² = ℓd²θ / dt². Из этого следует: ℓd²θ/dt² = — gsin θ, d²θ / dt² + d / ℓ sin θ = 0.
Крутящий момент
Для начала нужно определить этот показатель на маятниковом шарнире, используя силу, вызванную гравитацией (Fg): T = ℓ x Fg, где ℓ — векторы длины маятника.
Здесь самое время рассмотреть величину крутящего момента на маятнике: |T| = — mgℓ sinθ, где m — масса, g — ускорение силы тяжести, ℓ — длина, а θ — угол между вектором длины и гравитацией. Далее, самое время переписать момент импульса: L = r x p = mr x (ꞷ x r).
Просто величина углового момента и его производная по времени: |L| = mr² w = mℓ² d²θ / dt². Формула крутящего момента после всех вычислений будет выглядеть следующим образом: T = r x F = dL / dt.
Сохранение механической энергии
Такое уравнение можно получить с помощью одноимённого принципа. Формулируется он так: любой объект, падающий на вертикальное расстояние h, получит кинетическую энергию, равную той, которую потерял при падении. Изменение потенциальной энергии выражается: Δ U = mgh, тогда как кинетическая (отвес начал движение с покоя) представлена формулой: Δ K = 1/2 mu².
Поскольку, как известно, никакая энергия не теряется, выигрыш в одном должен быть равен потере в другом: 1/2 mu² = mgh.
Колебательные движения
Период колебаний математического маятника (простого гравитационного) зависит от его длины, локальной силы тяжести и в небольшой степени от максимального угла, от которого отвес отклоняется от вертикали θ 0, называемого амплитудой.
Он не зависит от массы груза. Если амплитуда ограничена малыми колебаниями, то на период T, время, необходимое для полного цикла является: T≈ 2 π √ L/g. При этом L — длина маятника, а g — местное ускорение гравитации.
Нужно сказать, что для небольших колебаний период не зависит от амплитуды. Такое свойство называется изохронизмом, именно оно стало причиной того, что маятники используются для хронометража. Последовательные колебания маятника, даже если они меняются по амплитуде, занимают одинаковое количество времени. Для большого размаха свойственно увеличение периода с каждым раскачиванием, поэтому он длиннее, чем задано уравнением, отражающим частоту колебаний математического маятника.
Период возрастает до бесконечности как только θ 0 приближается к 180°, так как это значение является нестабильной точкой равновесия для маятника. Истинный период может быть записан в нескольких различных формах, например, бесконечный ряд: T = 2 π √ L/g )1+ 1/16 θ²/º + 11/3072 θ ⁴/º + …). Разница между истинным и периодом небольших колебаний называется круговой ошибкой. В случае с типичными напольными часами, у которых маятник имеет размах 6° и, следовательно, амплитуду 3° (0,05 радиана), разница составит около 15 секунд в день.
Формула математического маятника, при малых колебаниях, когда он приближается к гармоническому осциллятору, и его движение, как функция времени t, находит выражение следующим образом: θ(t) = θₒ cos (2 π / T * t + ⱷ). Где фи (ⱷ) — постоянная величина, зависящая от начальных условий. Для маятников этот период незначительно меняется в зависимости от некоторых факторов, например:
- плавучесть и вязкостное сопротивление воздуха;
- масса нити или стержня;
- размер и форма отвеса и способы его прикрепления к шнуру;
- гибкость и растяжение нити.
Если необходимы точные расчёты, конечно, все эти поправки должны учитываться.
Составной маятник
Другое название — физический, представляет собой любое качающееся твёрдое тело, свободно вращающееся вокруг фиксированной горизонтальной оси. Соответствующая эквивалентная длина — L, а для расчёта времени используется расстояние от оси до центра колебаний. Эта точка расположена над центром массы на расстоянии от оси, традиционно называемым радиусом колебаний, который зависит от распределения веса груза.
Христиан Гюйгенс в 1673 году доказал, что точка вращения и центр колебаний взаимозаменяемы. Это означает, если какой-либо маятник перевёрнут и ротирован от оси, расположенной в его предыдущем центре колебаний, он будет иметь тот же период, что и раньше, и новый центр будет находиться в старой точке вращения.
В 1817 году Генри Кэтер использовал эту идею для создания обратимого маятника, теперь известного под именем создателя, для улучшения измерений ускорения под действием силы тяжести.
Историческая хроника
Одним из самых ранних известных применений маятника было устройство сейсмометра (I века) китайского учёного династии Хань Чжан Хэна. Его функция состояла в том, чтобы раскачивать и активировать один из серии рычагов после того, как он был нарушен тремором землетрясения, которое происходило далеко от места измерения. Освобождённый рычагом, маленький шарик выпадал из устройства в форме урны в одну из восьми горловин металлической жабы внизу, в восьми точках компаса, что указывало направление землетрясения.
Многие источники утверждают, что египетский астроном X века Ибн Юнус использовал маятник для измерения времени, но это была ошибка, возникшая в 1684 году с британским историком Эдвардом Бернардом.
В эпоху Возрождения большие маятники с ручной накачкой использовались в качестве источников энергии для ручных поршневых машин, таких как пилы, сильфоны и насосы. Леонардо Давинчи сделал много рисунков движения маятников, хотя и не осознавал его значения для хронометража.
Исследования Галилея
Итальянский учёный Галилео Галилей был первым, кто начал изучать свойства маятников, начиная примерно с 1602 года. Самый ранний существующий отчёт о его исследованиях содержится в письме Гвидо Убальдо дель Монте из Падуи от 29 ноября 1602 года. Его биограф и ученик, Винченцо Вивиани, утверждал, что его интерес был вызван около 1582 года, когда физик раскачивал люстры в соборе Пизы.
Галилей обнаружил важнейшее свойство, которое делает маятники полезными в качестве хронометриста, называемое изохронизмом; период маятника приблизительно не зависит от амплитуды или ширины качания. Он также обнаружил, что период не зависит от массы отвеса и пропорционален квадратному корню из длины всей конструкции. Сначала он использовал маятники свободного вращения в простых приложениях синхронизации.
Его друг — врач Санторио Санторий, используя наработки Галилея, изобрёл прибор, который измерял пульс пациента. В 1641 году Галилео задумал и продиктовал своему сыну Винченцо конструкцию маятниковых часов. Тот начал строительство, но не завершил его, поскольку умер в 1649 году. Так, появился первый гармонический осциллятор, использованный человеком.
Маятниковые часы
Первый образец построил в 1656 году голландский учёный Христиан Гюйгенс. Это было значительное улучшение по сравнению с существующими механическими часами. Их точность была улучшена с отклонений от 15 минут до 15 секунд в день. Маятники распространились по Европе, так как все существующие часы стали модифицироваться.
Английский учёный Роберт Гук изучил конический маятник (около 1666), который мог свободно колебаться в двух измерениях, а груз вращаться по кругу или эллипсу. Он использовал движение этого устройства в качестве модели для анализа орбитального движения планет. Гук предложил Исааку Ньютону в 1679 году свои наработки.
Он утверждал, что составляющие орбитального движения состояли из инерционного движения по касательному направлению и привлекательного движения в радиальном направлении. Это сыграло свою роль в формулировке Ньютоном закона всемирного тяготения. Роберт Гук также был ответственным за то, что ещё в 1666 году предположил, что маятник можно использовать для измерения силы тяжести.
Во время своей экспедиции в Кайенна (Французская Гвиана) в 1671, Жан Рише обнаружил, что там часы с маятником шли на 2,5 минуты медленнее, чем в Париже. Из этого он сделал вывод, что сила гравитации была ниже в Кайенне. В 1687 году Исаак Ньютон в Principia Mathematica показал, что это произошло потому, что Земля была не настоящей сферой, а слегка сплюснутой (сплющенной на полюсах) от действия центробежной силы из-за её вращения, это и вызывает увеличение силы гравитации.
Портативные маятники стали совершать рейсы в дальние страны, в качестве прецизионных гравиметров для измерения ускорения свободного падения в разных точках Земли, что в итоге привело к определению точной модели формы планеты. Затем последовало превращение исследований и выводов учёных в новые классы приборов, с дополнительными параметрами. Например:
- 1721 г. — маятник с температурной компенсацией;
- 1851 г. — маятник Фуко.
В 1930 году решение задачи по точному хронометражу было найдено, в 1921 был изобретён кварцевый генератор.
Источник
Математический маятник .
Математический маятник представляет из себя груз на нити.
Формула периода математического маятника:
(T=2 pi sqrt{dfrac{l}{g}} )
(l ) — длина нити
1. Вычислить период (T) математического маятника, если длина его подвеса
(l=0,9 м ) , ускорение свободного падения ( g=10м/с^2 ; )
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
2. Вычислить период (T) математического маятника, если длина его подвеса
(l=2,5 м ) , ускорение свободного падения ( g=10м/с^2 ; )
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 3.
Вычислить период (T) математического маятника, если длина его подвеса
(l=62,5 см ) , ускорение свободного падения ( g=10м/с^2 ; )
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 4.
Найти длину подвеса математического маятника, если его период ( T=1,884 с )
, ускорение свободного падения ( g=10м/с^2 ; )
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 5.
Какую длину подвеса должен иметь математический маятник, чтобы его период был равен 3,14 с ?
Ускорение свободного падения ( g=10м/с^2 ; )
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 6.
При проведении лабораторной работы по вычислению ускорения свободного падения
математический маятник длиной (l=1 м ) совершил за время (t=34 с )
17 колебаний.
Какое значение ускорения свободного падения получено из данных опыта?
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 6.(Другое решение вывод формулы в общем виде)
При проведении лабораторной работы по вычислению ускорения свободного падения
математический маятник длиной (l=1 м ) совершил за время (t=34 с )
17 колебаний.
Какое значение ускорения свободного падения получено из данных опыта?
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 7.
Найти длины (l_1 и l_2 ) математических маятников, если
за одно и то же время один математический маятник совершает (N_1=50 ) колебаний, а другой (N_2=30 )
колебаний.
Разность длин маятников (l_2-l_1=0,32 метра )
Дать ответ в сантиметрах
Показать ответ
Показать решение
Видеорешение