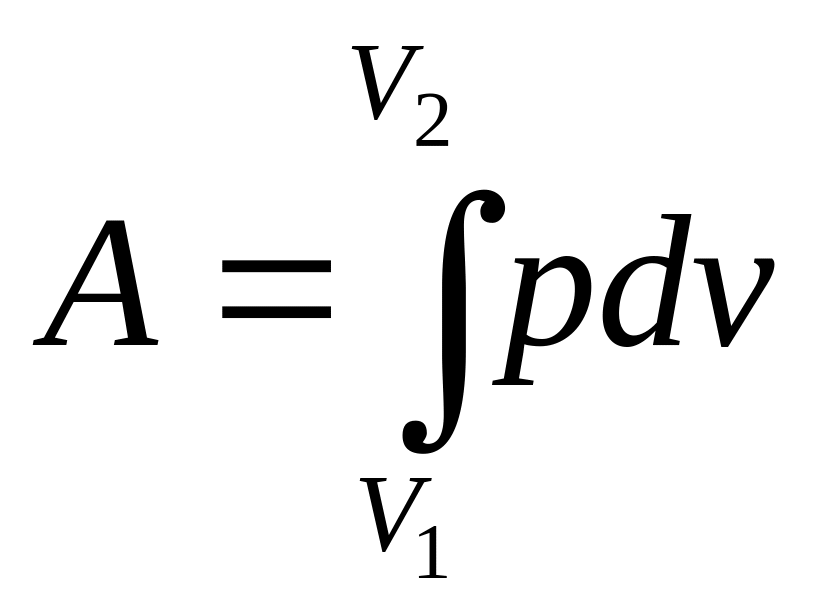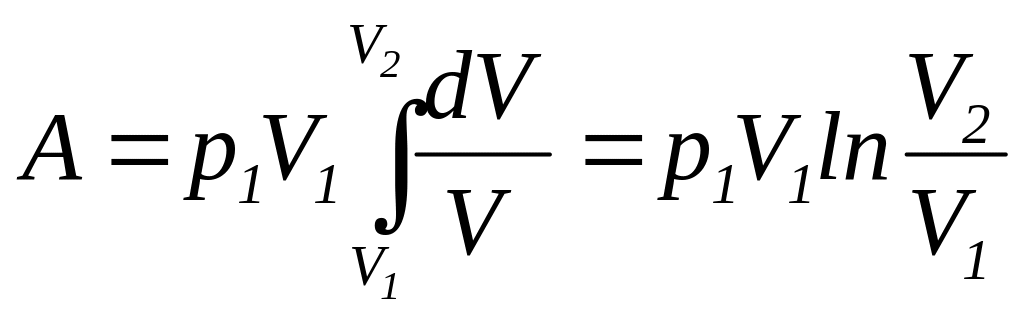Как найти работу газа при изотермическом расширении

Изменение
объема газа, т.е. его расширение или
сжатие, можно произвести так, чтобы
температура газа оставалась постоянной.
Такой процесс изменения состояния газа
или другой системы, который проходит
при постоянной температуре, называется
изотермическим. Для того чтобы процесс
в системе мог протекать изотермически,
она должна быть помещена в среду с
постоянной температурой, к примеру, в
термостат — аппарат, в котором специальное
устройство — терморегулятор —
автоматически поддерживает температуру
постоянной. Расширяясь в термостате,
т.е. при T=const,
система производит некоторую работу,
которая по первому началу термодинамики
равна:

(109)

где

― количество теплоты, поглощенной
системой от термостата, а

― изменение ее внутренней энергии.

В
случае идеального газа внутренняя
энергия зависит только от температуры
и не зависит от занимаемого им объема.
Поэтому при изотермическом расширении
или сжатии идеального газа его внутренняя
энергия остается неизменной при

и

.
Первое начало термодинамики (109) в этом
случае принимает вид:

(110)

(111)

A=Q

Это
равенство показывает, что при изотермическом
расширении объема идеального газа
работа

может производится только за счет
поглощаемого им тепла

.
Если газ изотермически расширяется
(
),
то он совершает положительную работу
(
)
и согласно равенству (110) получает извне
(от среды термостата) такое же количество
тепла (
).
Если же внешние силы совершают над газом
работу при его изотермическом сжатии
(
,
),
то он отдает такое же количество тепла
(
).
Таким образом, в случае изотермического
расширения газ полностью преобразует
подводимое к нему тепло в совершаемую
работу. Наоборот, при изотермическом
сжатии работа, затраченная на сжатие,
полностью преобразуется в отдаваемое
газом внешней среде (среде термостата)
тепло. Именно по этой причине внутренняя
энергия и температура газа остаются
неизменными. Газ при изотермическом
процессе ведет себя как тело с бесконечно
большой теплоемкостью. Математически
это следует из общего определения
теплоемкости; обозначив изотермическую
теплоемкость через С_Т,
получаем

,
т. к.

,

Из
сказанного выше ясно, что для того, чтобы
расширение газа могло происходить
изотермически, ему необходимо непрерывно
передавать тепло извне. Наоборот, чтобы
сжатие газа протекало изотермически,
от него необходимо непрерывно отбирать
тепло. Изотермический процесс,
следовательно, возможен лишь при идеально
хорошем обмене теплом между газом и
внешней средой (средой термостата).
Практически приблизиться к изотермическому
процессу можно, заставляя протекать
его настолько медленно, чтобы температура
газа все время успевала выравниваться
с температурой окружающей среды.

Вычислим
работу, совершаемую идеальным газом
при изотермическом изменении его объема
от V₁
до V₂.
Работа, производимая любой системой
при изменении ее объема, как мы видели,
определяется интегралом

(112)

Чтобы
произвести интегрирование, нужно знать,
как при рассматриваемом процессе
давление p
связано с объемом V,
т.е. необходимо знать уравнение процесса
в переменных p,
V.
Уравнение изотермического процесса
для идеального газа получается
непосредственно из его уравнения
состояния

(113)

Так
как при изотермическом процессе T=const,
то для данной массы газа

и, следовательно,

(114)

где
p₁
и V₁
― значения давления и объема газа в
начальном состоянии. Таким образом, при
изотермическом процессе давление и
объем идеального газа связаны между
собой законом Бойля-Мариотта. Выражая
из (114) давление газа через объем и
значение параметров в начальном состоянии

(115)

и
подставляя полученное выражение в
(112), находим

(116)

Так
как

,
то формулу для работы идеального газа
при изотермическом изменении его объема
можно представить в виде

(117)

Из
(116) и (117) видно, что работа идеального
газа при изотермическом процессе
изменения объема зависит не от разности
объемов как для изобарического процесса,
между которыми происходит расширение
или сжатие, а от их отношения (т. е. степени
расширения или сжатия газа).

Так
как при изотермическом процессе работа
A
производится идеальным газом за счет
передаваемого ему извне тепла, то
полученные выше формулы могут в равной
мере служить как для определения
совершаемой газом изотермической
работы, так и для расчета количества
теплоты Q,
необходимой для его изотермического
расширения или сжатия

(118)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

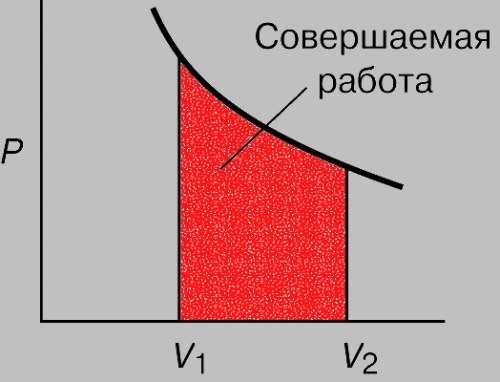
Как определить работу при изотермическом процессе

При изотермическом процессе, который протекает при постоянной температуре, газ выполняет работу за счет расширения. Расширение газа характеризуется его объемом, который изменяется в зависимости от изменения давления газа, обусловленного внешними воздействиями.

Вам понадобится

— герметичный сосуд с поршнем;
— весы;
— термометр;
— линейка.

Инструкция

Рассчитайте работу газа при постоянной температуре. Для этого определите, какой газ выполняет работу, и рассчитайте его молярную массу. С помощью периодической таблицы найдите молекулярную массу, которая численно равна молярной массе, измеренной в г/моль.

Найдите массу газа. Для этого откачайте воздух из герметичного сосуда и взвесьте его на весах. После этого закачайте газ, работа которого определяется, и снова взвесьте сосуд. Разность масс пустого и заполненного сосудов и будет равна массе газа. Измеряйте ее в граммах.

Измерьте при помощи термометра температуру газа. При изотермическом процессе она будет постоянна. Если измерение производится при комнатной температуре, достаточно измерить температуру окружающего воздуха. Измерения произведите в Кельвинах. Для этого к температуре, измеренной в градусах Цельсия, прибавьте число 273.

Определите начальный и конечный объем газа при выполнении работы. Для этого сосуд берите с подвижным поршнем, и, вычисляя уровень его подъема, рассчитайте первичный и вторичный объем геометрическими методами. Для этого используйте формулу для объема цилиндра V=π•R²•h, где π≈3,14, R – радиус цилиндра, h его высота.

Рассчитайте работу газа при изотермическом процессе. Для этого поделите массу газа m на его молярную массу M. Полеченный результат умножьте на универсальную газовую постоянную R=8,31 и значение температуры Т в Кельвинах. Полученный результат умножьте на натуральный логарифм из отношения конечного и начального объемов V2 и V1, A = m/M•R•T•ln(V2/V1).

В том случае, когда известно количество теплоты Q, которое получило тело при изотермическом процессе, используйте второе начало термодинамики Q = ∆U + A. Где A – работа газа, а ΔU – изменение его внутренней энергии. Поскольку изменение внутренней энергии зависит от температуры, а при изотермическом процессе она остается постоянной, то ΔU=0. В этом случае работа газа равна теплоте, переданной ему Q = A.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

From Wikipedia, the free encyclopedia

«Isothermal» redirects here. For other uses, see Isotherm.

In thermodynamics, an isothermal process is a type of thermodynamic process in which the temperature T of a system remains constant: ΔT = 0. This typically occurs when a system is in contact with an outside thermal reservoir, and a change in the system occurs slowly enough to allow the system to be continuously adjusted to the temperature of the reservoir through heat exchange (see quasi-equilibrium). In contrast, an adiabatic process is where a system exchanges no heat with its surroundings (Q = 0).

Simply, we can say that in an isothermal process

while in adiabatic processes:

Etymology[edit]

The adjective «isothermal» is derived from the Greek words «ἴσος» («isos») meaning «equal» and «θέρμη» («therme») meaning «heat».

Examples[edit]

Isothermal processes can occur in any kind of system that has some means of regulating the temperature, including highly structured machines, and even living cells. Some parts of the cycles of some heat engines are carried out isothermally (for example, in the Carnot cycle).^[1] In the thermodynamic analysis of chemical reactions, it is usual to first analyze what happens under isothermal conditions and then consider the effect of temperature.^[2] Phase changes, such as melting or evaporation, are also isothermal processes when, as is usually the case, they occur at constant pressure.^[3] Isothermal processes are often used as a starting point in analyzing more complex, non-isothermal processes.

Isothermal processes are of special interest for ideal gases. This is a consequence of Joule’s second law which states that the internal energy of a fixed amount of an ideal gas depends only on its temperature.^[4] Thus, in an isothermal process the internal energy of an ideal gas is constant. This is a result of the fact that in an ideal gas there are no intermolecular forces.^[4] Note that this is true only for ideal gases; the internal energy depends on pressure as well as on temperature for liquids, solids, and real gases.^[5]

In the isothermal compression of a gas there is work done on the system to decrease the volume and increase the pressure.^[4] Doing work on the gas increases the internal energy and will tend to increase the temperature. To maintain the constant temperature energy must leave the system as heat and enter the environment. If the gas is ideal, the amount of energy entering the environment is equal to the work done on the gas, because internal energy does not change. For isothermal expansion, the energy supplied to the system does work on the surroundings. In either case, with the aid of a suitable linkage the change in gas volume can perform useful mechanical work. For details of the calculations, see calculation of work.

For an adiabatic process, in which no heat flows into or out of the gas because its container is well insulated, Q = 0. If there is also no work done, i.e. a free expansion, there is no change in internal energy. For an ideal gas, this means that the process is also isothermal.^[4] Thus, specifying that a process is isothermal is not sufficient to specify a unique process.

Details for an ideal gas[edit]

Figure 1. Several isotherms of an ideal gas on a p-V diagram, where p for pressure and V the volume.

For the special case of a gas to which Boyle’s law^[4] applies, the product pV (p for gas pressure and V for gas volume) is a constant if the gas is kept at isothermal conditions. The value of the constant is nRT, where n is the number of moles of the present gas and R is the ideal gas constant. In other words, the ideal gas law pV = nRT applies.^[4] Therefore:

p={nRT over V}={{text{constant}} over V}

holds. The family of curves generated by this equation is shown in the graph in Figure 1. Each curve is called an isotherm, meaning a curve at a same temperature T. Such graphs are termed indicator diagrams and were first used by James Watt and others to monitor the efficiency of engines. The temperature corresponding to each curve in the figure increases from the lower left to the upper right.

Calculation of work[edit]

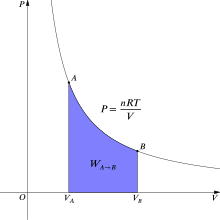
Figure 2. The purple area represents the work for this isothermal change.

In thermodynamics, the reversible work involved when a gas changes from state A to state B is^[6]

$W_{{Ato B}}=-int _{{V_{A}}}^{{V_{B}}}p,dV$

where p for gas pressure and V for gas volume. For an isothermal (constant temperature T), reversible process, this integral equals the area under the relevant PV (pressure-volume) isotherm, and is indicated in purple in Figure 2 for an ideal gas. Again, p = nRT/V applies and with T being constant (as this is an isothermal process), the expression for work becomes:

$W_{{Ato B}}=-int _{{V_{A}}}^{{V_{B}}}p,dV=-int _{{V_{A}}}^{{V_{B}}}{frac {nRT}{V}}dV=-nRTint _{{V_{A}}}^{{V_{B}}}{frac {1}{V}}dV=-nRTln {{frac {V_{B}}{V_{A}}}}$

In IUPAC convention, work is defined as work on a system by its surroundings. If, for example, the system is compressed, then the work is done on the system by the surrounding so the work is positive and the internal energy of the system increases. Conversely, if the system expands (i.e., system surrounding expansion, so free expansions not the case), then the work is negative as the system does work on the surroundings and the internal energy of the system decreases.

It is also worth noting that for ideal gases, if the temperature is held constant, the internal energy of the system U also is constant, and so ΔU = 0. Since the First Law of Thermodynamics states that ΔU = Q + W in IUPAC convention, it follows that Q = −W for the isothermal compression or expansion of ideal gases.

Example of an isothermal process[edit]

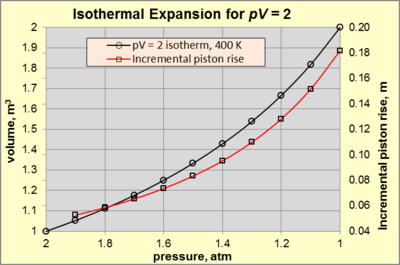
Figure 3. Isothermal expansion of an ideal gas. Black line indicates continuously reversible expansion, while the red line indicates stepwise and nearly reversible expansion at each incremental drop in pressure of 0.1 atm of the working gas.

The reversible expansion of an ideal gas can be used as an example of work produced by an isothermal process. Of particular interest is the extent to which heat is converted to usable work, and the relationship between the confining force and the extent of expansion.

During isothermal expansion of an ideal gas, both p and V change along an isotherm with a constant pV product (i.e., constant T). Consider a working gas in a cylindrical chamber 1 m high and 1 m² area (so 1m³ volume) at 400 K in static equilibrium. The surroundings consist of air at 300 K and 1 atm pressure (designated as p_surr). The working gas is confined by a piston connected to a mechanical device that exerts a force sufficient to create a working gas pressure of 2 atm (state A). For any change in state A that causes a force decrease, the gas will expand and perform work on the surroundings. Isothermal expansion continues as long as the applied force decreases and appropriate heat is added to keep pV = 2 [atm·m³] (= 2 atm × 1 m³). The expansion is said to be internally reversible if the piston motion is sufficiently slow such that at each instant during the expansion the gas temperature and pressure is uniform and conform to the ideal gas law. Figure 3 shows the p–V relationship for pV = 2 [atm·m³] for isothermal expansion from 2 atm (state A) to 1 atm (state B).

The work done (designated ${displaystyle W_{Ato B}}$ ) has two components. First, expansion work against the surrounding atmosphere pressure (designated as W_pΔV), and second, usable mechanical work (designated as W_mech). The output W_mech here could be movement of the piston used to turn a crank-arm, which would then turn a pulley capable of lifting water out of flooded salt mines.

${displaystyle W_{Ato B}=-p,Vleft(ln {frac {V_{B}}{V_{A}}}right)=-W_{pDelta V}-W_{rm {mech}}}$

The system attains state B (pV = 2 [atm·m³] with p = 1 atm and V = 2 m³) when the applied force reaches zero. At that point, ${displaystyle W_{Ato B}}$ equals –140.5 kJ, and W_pΔV is –101.3 kJ. By difference, W_mech = –39.1 kJ, which is 27.9% of the heat supplied to the process (- 39.1 kJ / — 140.5 kJ). This is the maximum amount of usable mechanical work obtainable from the process at the stated conditions. The percentage of W_mech is a function of pV and p_surr, and approaches 100% as p_surr approaches zero.

To pursue the nature of isothermal expansion further, note the red line on Figure 3. The fixed value of pV causes an exponential increase in piston rise vs. pressure decrease. For example, a pressure decrease from 2 to 1.9 atm causes a piston rise of 0.0526 m. In comparison, a pressure decrease from 1.1 to 1 atm causes a piston rise of 0.1818 m.

Entropy changes[edit]

Isothermal processes are especially convenient for calculating changes in entropy since, in this case, the formula for the entropy change, ΔS, is simply

${displaystyle Delta S={frac {Q_{text{rev}}}{T}}}$

where Q_rev is the heat transferred (internally reversible) to the system and T is absolute temperature.^[7] This formula is valid only for a hypothetical reversible process; that is, a process in which equilibrium is maintained at all times.

A simple example is an equilibrium phase transition (such as melting or evaporation) taking place at constant temperature and pressure. For a phase transition at constant pressure, the heat transferred to the system is equal to the enthalpy of transformation, ΔH_tr, thus Q = ΔH_tr.^[3] At any given pressure, there will be a transition temperature, T_tr, for which the two phases are in equilibrium (for example, the normal boiling point for vaporization of a liquid at one atmosphere pressure). If the transition takes place under such equilibrium conditions, the formula above may be used to directly calculate the entropy change^[7]

${displaystyle Delta S_{text{tr}}={frac {Delta H_{text{tr}}}{T_{text{tr}}}}}$

Another example is the reversible isothermal expansion (or compression) of an ideal gas from an initial volume V_A and pressure P_A to a final volume V_B and pressure P_B. As shown in Calculation of work, the heat transferred to the gas is

${displaystyle Q=-W=nRTln {frac {V_{text{B}}}{V_{text{A}}}}}$ .

This result is for a reversible process, so it may be substituted in the formula for the entropy change to obtain^[7]

${displaystyle Delta S=nRln {frac {V_{text{B}}}{V_{text{A}}}}}$ .

Since an ideal gas obeys Boyle’s Law, this can be rewritten, if desired, as

${displaystyle Delta S=nRln {frac {P_{text{A}}}{P_{text{B}}}}}$ .

Once obtained, these formulas can be applied to an irreversible process, such as the free expansion of an ideal gas. Such an expansion is also isothermal and may have the same initial and final states as in the reversible expansion. Since entropy is a state function (that depends on an equilibrium state, not depending on a path that the system takes to reach that state), the change in entropy of the system is the same as in the reversible process and is given by the formulas above. Note that the result Q = 0 for the free expansion can not be used in the formula for the entropy change since the process is not reversible.

The difference between the reversible and irreversible is found in the entropy of the surroundings. In both cases, the surroundings are at a constant temperature, T, so that ΔS_sur = −Q/T; the minus sign is used since the heat transferred to the surroundings is equal in magnitude and opposite in sign to the heat Q transferred to the system. In the reversible case, the change in entropy of the surroundings is equal and opposite to the change in the system, so the change in entropy of the universe is zero. In the irreversible, Q = 0, so the entropy of the surroundings does not change and the change in entropy of the universe is equal to ΔS for the system.

References[edit]

^ Keenan, J. H. (1970). «Chapter 12: Heat-engine cycles». Thermodynamics. Cambridge, Massachusetts: MIT Press.
^ Rock, P. A. (1983). «Chapter 11: Thermodynamics of chemical reactions». Chemical Thermodynamics. Mill Valley, CA: University Science Books. ISBN 0-935702-12-1.
^ ^a ^b Petrucci, R. H.; Harwood, W. S.; Herring, F. G.; Madura, J. D. (2007). «Chapter 12». General Chemistry. Upper Saddle River, NJ: Pearson. ISBN 978-0-13-149330-8.
^ ^a ^b ^c ^d ^e ^f Klotz, I. M.; Rosenberg, R. M. (1991). «Chapter 6, Application of the first law to gases». Chemical Thermodynamics. Meno Park, CA: Benjamin.^{[ISBN missing]}
^ Adkins, C. J. (1983). Equilibrium Thermodynamics. Cambridge: Cambridge University Press.^{[ISBN missing]}
^ Atkins, Peter (1997). «Chapter 2: The first law: the concepts». Physical Chemistry (6th ed.). New York, NY: W. H. Freeman and Co. ISBN 0-7167-2871-0.
^ ^a ^b ^c Atkins, Peter (1997). «Chapter 4: The second law: the concepts». Physical Chemistry (6th ed.). New York, NY: W. H. Freeman and Co. ISBN 0-7167-2871-0.

Источник

Первый закон термодинамики

Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Работа газа в изобарном процессе
Работа газа в произвольном процессе
Работа, совершаемая над газом
Применение первого закона термодинамики к изопроцессам
Адиабатный процесс

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.

Начнём с обсуждения работы газа.

Газ, находящийся в сосуде под поршнем, действует на поршень с силой F=pS , где — давление газа, — площадь поршня. Если при этом поршень перемещается, то газ совершает работу.

При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).

к оглавлению ▴

Работа газа в изобарном процессе

Предположим, что газ расширяется при постоянном давлении . Тогда сила , с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние Delta x (рис. 1).

Рис. 1.

Работа газа равна:

Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:

(1)

Если V_1 и V_2 — начальный и конечный объём газа, то для работы газа имеем: . Изобразив данный процесс на -диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).

Рис. 2. Работа газа как площадь

Пусть теперь газ изобарно сжимается от объёма V_1 до объёма V_2 . С помощью аналогичных рассуждений приходим к формуле:

Но , и снова получается формула (1).

Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.

Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.

к оглавлению ▴

Работа газа в произвольном процессе

Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.

Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление будет оставаться приблизительно постоянным. Газ совершит малую работу dA=p dV . Тогда работа газа во всём процессе найдётся суммированием этих малых работ:

$A=int_{V_1}^{V_2}p dV.$

Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):

Рис. 3. Работа газа как площадь

к оглавлению ▴

Работа, совершаемая над газом

Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу {A} , которую поршень совершает над газом.

Если газ действует на поршень с силой vec{F} , то по третьему закону Ньютона поршень действует на газ с силой , равной силе vec{F} по модулю и противоположной по направлению: (рис. 4).

Рис. 4. Внешняя сила , действующая на газ

Следовательно, работа поршня {A} равна по модулю и противоположна по знаку работе газа:

{A}

Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна . Наоборот, при сжатии работа газа отрицательна , а работа, совершаемая поршнем над газом, положительна 0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.

Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа {A} .

Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.

Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа {A} , то изменение внутренней энергии тела будет равно:

(2)

Нас больше всего интересует случай, когда тело является газом. Тогда {A} (где , как всегда, есть работа самого газа). Формула (2) принимает вид: , или

(3)

Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.

Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.

к оглавлению ▴

Применение первого закона термодинамики к изопроцессам

Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.

1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:

Q = A.

Всё подведённое к газу тепло идёт на совершение газом работы.

2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: A = 0 . Тогда первый закон термодинамики даёт:

Всё тепло, переданное газу, идёт на изменение его внутренней энергии.

3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:

к оглавлению ▴

Адиабатный процесс

Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.

Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.

Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.

При адиабатном процессе Q=0 . Из первого закона термодинамики получаем: , или .

В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.

Наоборот, в процессе адиабатного сжатия будет A < 0 , поэтому : газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.

Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).

Рис. 5. Сравнительный ход изотермы и адиабаты

В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?

При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.

А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Как определить работу при изотермическом процессе

Etymology[edit]

Examples[edit]

Details for an ideal gas[edit]

Calculation of work[edit]

Example of an isothermal process[edit]

Entropy changes[edit]

See also[edit]

References[edit]

Первый закон термодинамики

Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.

Работа газа в изобарном процессе

Работа газа в произвольном процессе

Работа, совершаемая над газом

Применение первого закона термодинамики к изопроцессам

Адиабатный процесс

Не пропустите также: