Как найти работу газа при изохорном процессе - Avtoru.top

Изохорный процесс
(V
= сonst).

Так как система
не изменяет своего объема, она не
совершает работы над внешними телами

; А=0
, тогда
, (3.4.1)

При изохорном
процессе работа газом не совершается,
а поступающее (или отдаваемое) тепло
равно изменению внутренней энергии.

Изобарный процесс
(P=сonst).

При постоянном
давлении объем системы меняется, и она
может совершать работу
,

. (3.4.2)

Используя уравнение
состояния идеального газа

(P
= Const),
можно записать

. (3.4.3)

Из I
начала термодинамики

откуда

. (3.4.4)

При изобарическом
процессе часть поступающего тепла
расходуется на увеличение внутренней
энергии, а часть – на совершение
макроскопической работы.

Изотермический
процесс (T
= сonst)

При изотермическом
процессе температура системы не меняется
и, следовательно
.
Тогда из I
начала термодинамики
,
,
т.е.
,
или Q
= A΄.
Из уравнения состояния идеального газа

можно выразить Р:
,
тогда

. (3.4.5)

Следовательно,

При изотермическом
процессе внутренняя энергия газа не
меняется, вся полученная теплота идет
на совершение работы.

Адиабатический
процесс ().

При адиабатическом
процессе к системе не подводится теплота.
В этом случае
.
Из уравнения адиабаты

давление
.
Тогда

и

. (3.4.6)

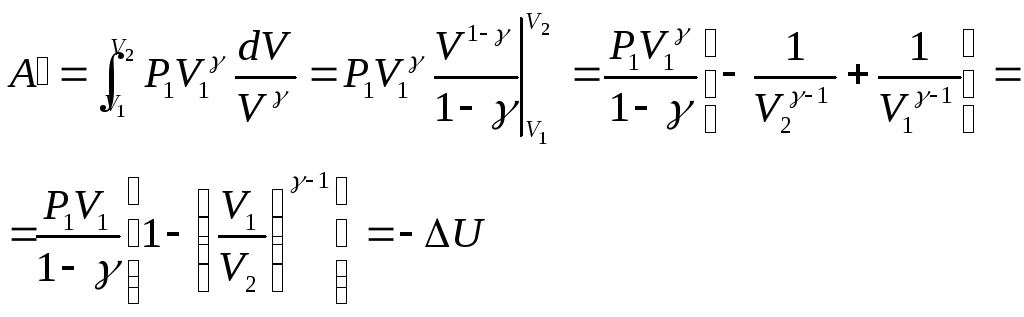
При адиабатическом
процессе работа совершается газом за
счет уменьшения его внутренней энергии.

Найдем выражение
для вычисления работы в политропическом
процессе. Будем использовать уравнение
политропы в параметрах (p,V).
Если известны значения давления и объема
в некотором состоянии
,
тогда

. (3.4.7.)

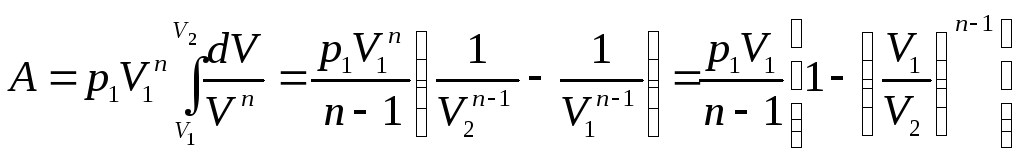
Покажем, что
изотермический, изобарный, изохорный
и адиабатный процессы являются частными
случаями политропического процесса. В
адиабатном процессе
,
следовательно

и уравнения политропы (3.3.12), (3.3.13), (3.3.14)
переходят в уравнения адиабаты в виде
(3.3.4), (3.3.5) и (3.3.6) соответственно.

Теплоемкость при
изотермическом процессе равна
бесконечности, следовательно
.
Из уравнений (3.3.12) и (3.3.14) получаем условие
,
а выражение (3.3.13) переходит в закон
Бойля-Мариотта
.
Показатель политропы в изобарном
процессе равен нулю, поэтому из (3.3.12)
получаем уравнение изобары
.
Для изохорного процесса показатель
.
Уравнение политропы (3.3.14) преобразуем
к виду

, (3.4.8)

откуда получается
уравнение изохоры
.

Рассмотрим процесс
не являющийся квазиравновесным –
расширение газа в пустоту. Пусть имеется
сосуд в адиабатически изолированной
оболочке, разделенный на две части. В
одной части давление

и температура
,
в другой части газа нет. Если перегородку
убрать мгновенно, то возникает
неравновесное состояние с потоками
частиц, отличными от нуля. В дальнейшем,
в процессе выравнивания параметров,
потоки затухают и через некоторый
промежуток времени в сосуде устанавливается
равновесное состояние при температуре
.
Так как перегородка убирается мгновенно,
то газ не совершает работу против внешних
сил; так как система адиабатически
изолирована, количество теплоты газу
не передается и не отнимается,
следовательно, его внутренняя энергия
не изменяется. В модели идеального газа,
это означает, что температура газа
остается постоянной.

К процессу расширения
газа в пустоту нельзя применить результат,
полученный для квазиравновесного
процесса адиабатного расширения, для
которого
.

Применим полученные
результаты к анализу процесса
распространения звука в газах.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Определение

Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.

Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:

U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV

i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.

Изменение внутренней энергии идеального газа в изопроцессах

Основная формула	ΔU=32·mMRT=32νRT=32νR(T2−T1)
Изотермический процесс	ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной.
Изобарное расширение	ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV
Изохорное увеличение давления	ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp
Произвольный процесс	ΔU=32νR(T2−T1)=32(p2V2−p1V1)

Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?

Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.

Работа идеального газа

Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.

Механическая работа вычисляется по формуле:

A=Fscosα

Перемещение равно разности высот поршня в конечном и начальном положении:

s=h2−h1

Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:

Работа идеального газа

F=pS

p — давление газа, S — площадь поршня

Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:

A‘=p(V2−V1)=pΔV>0

Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.

Работа идеального газа при изобарном сжатии:

A‘=p(V2−V1)=pΔV<0

Работа идеального газа при нагревании газа:

A‘=νRΔT=νR(T2−T1)=mMνRΔT

Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.

Геометрический смысл работы в термодинамике

В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).

Примеры графических задач

Изобарное расширение: A‘=p(V2−V1) A‘>0
Изобарное сжатие: A‘=p(V2−V1) A‘<0
Изохорное охлаждение: V=const A‘=0
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0
Замкнутый цикл: 1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1)
Произвольный процесс: A‘=p1+p22(V2−V1)

Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A₂ к A₁ в этих процессах.

Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:

A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV

A1=p(V2−V1)=p(5V−V)=4pV

Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.

Задание EF17505

Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?

Для каждой величины подберите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Определить по графику, как меняется давление.
Определить, как меняется объем.
Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.

Решение

На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.

Ответ: 123

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17758

Один моль аргона, находящийся в цилиндре при температуре T₁=600 K и давлении p₁=4⋅10⁵ Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p₂=10⁵ Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?

Алгоритм решения

1.Записать исходные данные.

2.Записать уравнение состояния идеального газа.

3.Записать формулу для расчета внутренней энергии газа.

4.Используя первое начало термодинамики, выполнить общее решение задачи.

5.Подставив известные данные, вычислить неизвестную величину.

Решение

Запишем исходные данные:

• Начальная температура газа: T₁ = 600 К.

• Начальное давление: p₁ = 4∙10⁵ Па.

• Конечное давление: p₂ = 10⁵ Па.

• Работа, совершенная газом: A = 2493 Дж.

Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:

pV=νRT

Внутренняя энергия одноатомного идеального газа пропорциональна температуре:

U=32νRT

Внутренняя энергия аргона до расширения и после него:

U1=32νRT1

U2=32νRT2

Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:

T=constV

T1V1=T2V2

Выразим конечную температуру:

T2=T1V1V2

Составим уравнение состояния газа для состояний аргона 1 и 2:

p1V1=νRT1

p2V2=νRT2

Отсюда:

νR=p1V1T1=p2V2T2

Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:

V1V2=p2T1p1T2

Подставим это отношение в формулу для конечной температуры:

T2=T1V1V2=p2T12p1T2

Отсюда:

T2=T1√p2p1

Отсюда внутренняя энергия газа в состоянии 2 равна:

U2=32νRT1√p2p1

Уменьшение внутренней энергии аргона составило (изначально она была выше):

ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)

В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:

ΔU=Q+A

Следовательно, газ отдал следующее количество теплоты:

Q=ΔU−A=32νRT1(1−√p2p1)−A

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17966

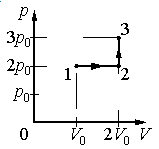
Идеальный газ переводят из состояния 1 в состояние 3 так, как показано на графике зависимости давления газа от объёма. Работа, совершённая при этом газом, равна

Ответ:

а) р₀V₀

б) 2р₀V₀

в) 4р₀V₀

г) 6р₀V₀

Алгоритм решения

1.Определить, на каком участке графика совершается работа.

2.Записать геометрический смысл работы.

3.Извлекая данные из графика, вычислить работу, совершенную газом.

Решение

Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.

Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).

Давление газа при этом равно 2p₀, а объем равен разности 2V₀ и V₀. Следовательно, работа, совершенная газом, будет равна произведению:

A=2p0(2V0−V0)=2p0V0

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 15.1k

Источник

Сергей Сергеевич Соев

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Определение 1

Изохорический или изохорный процесс — один из основных термодинамических процессов, который происходит исключительно при постоянном объёме.

Рисунок 1. Изохорный процесс. Автор24 — интернет-биржа студенческих работ

Для осуществления изохорного процесса в идеальном газе или жидкости достаточно постепенно нагревать или охлаждать действующее вещество в сосуде, который не изменяет своего изначального объёма и находится в замкнутом пространстве.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

При изохорическом процессе общее давление идеального газа будет всегда прямо пропорционально его начальной температуре. Графики, которые изображают указанное физическое явление линиями, называются изохоры.

Для идеального газа они являются прямыми и стабильными во всех диаграммах, которые связывают такие основные параметры:

$T$ (температура рабочего тела);
$V$ (объем исследуемого вещества);
$P$ (внутреннее давление).

История возникновения теории изохорного процесса

Наиболее часто первые научные исследования изохорного процесса связывают с физиком-теоретиком Гийомом Амонтоном . В своей первой работе «Парижские мемуары», которая была выпущена в 1702 году, изобретатель детально описал поведение идеального газа в фиксированном объёме внутри так называемого «воздушного стабильного термометра». Жидкость в нём находится всегда в равновесии под влиянием атмосферного давления и энергии исследуемого элемента в резервуаре. При постепенном нагревании давление и объем в замкнутом пространстве увеличивается, и жидкость вытесняется в следующий, выступающий столб.

«Изохорный процесс в термодинамике» 👇

В начале 1801 года физик Джон Дальтон в двух своих известных эссе опубликовал новый эксперимент, в котором определил, что все пары и газы, исследованные при неизменном давлении, одинакового расширяются и уменьшаются при изменении температуры, если соответствующий начальный и конечный показатель были одинаковы. Данный закон получил в науке название закона Гей-Люссака, так как именно этот исследователь вскоре смог провести самостоятельные опыты и подтвердил одинаковое распределение различных газов, получив в итоге практически тот самый коэффициент, что и Дальтон. Впоследствии ученый объединил свою теорию с законом Бойля — Мариотта, что позволило более понятно описывать в том числе и сам изохорный процесс.

Первый закон термодинамики для изохорного процесса

Рисунок 2. Закон Шарля. Автор24 — интернет-биржа студенческих работ

Простая формулировка первого термодинамического закона может звучать приблизительно так: изменение внутренней энергии той или иной концепции возможно только при наличии внешнего воздействия.

То есть иными словами, чтобы в системе произошли любые изменения необходимо приложить усилия извне. Именно первый закон термодинамики устанавливает, почему все многочисленные попытки исследователей потерпели неудачу, ведь ученые так и не смогли изобрести «вечный двигатель», существование которого считается абсолютно невозможным согласно этому самому закону.

Замечание 1

Формула первого закона термодинамики записывается таким образом: $Q = ΔU + A$, где $Q$ –количество теплоты, $ΔU$ – сумма изменения внутренней энергии и $A$ – работа системы.

Изохорным процессом в термодинамике называют физическим процесс, происходящий при постоянном, равномерном объеме. То есть, если в газе или жидкости нагреть определенное вещество в сосуде, произойдет изучаемое явление, так как объем элементов в такой системе останется неизменным. Это условие имеет существенное влияние и на первый термодинамический закон термодинамики, проходящий в основном при изохорном процессе.
В изохорном процессе объем рабочих тел $V$ является постоянной константой, следовательно, газ работы не совершает $A = 0$.

Из этого возможно вывести следующую формулу: $Q = ΔU = U (T_2) – U (T_1)$. Здесь $U (T_1)$ и $U (T_2)$ — внутренние энергии идеального газа, которые были зафиксированы в начальном и конечном положениях. Внутренняя энергия исследуемого элемента напрямую зависит только от первостепенной температуры (закон Джоуля).

При изохорном систематическим нагревании все тепло материального тела поглощается газом $(Q > 0)$, и его внутренняя энергия постепенно увеличивается. При охлаждении тепло будет отдаваться внешним элементам $(Q $

Метод исследования данного процесса заключается в следующем:

изначально выводится уравнение физического явления (взаимосвязь между начальными и конечными показателями рабочего тела);
вычисляется дальнейшая работа изменения объема газа;
устанавливается точное количество теплоты, отведенное или подведенной к исследуемому объекту;
определяется изменение внутренней энергии и энтропии концепции в процессе.

Поскольку внутренняя энергия является главной функцией состояния материального тела, то формулы изохорного процесса справедливы для любого термодинамического процесса идеального газа.

Применение эффекта изохорного процесса

Рисунок 3. Уравнение состояния. Автор24 — интернет-биржа студенческих работ

Изохорный процесс зачастую осуществляется в жидкостях и газах, расположенных в замкнутом сосуде с постоянным объемом. При этом явлении система не выполняет работы, и подведённая теплота $Q$ полностью расходуется на изменение тепловой энергии: $dU = Dq$.

Замечание 2

Следовательно, теплоёмкость при неизменном объёме будет всегда значительно меньше аналогичного параметра при постоянном давлении.

В идеальном газе в ходе изохорного процесса давление прямо пропорционально температуре – закон Шарля. Для неидеального газа закон Шарля невозможно применить, так как часть сообщённой газу теплоты идет строго на увеличение энергетического потенциала взаимодействия элементарных частиц.

При идеальном цикле Отто, который максимально приближённо внедрен в бензиновый двигатель внутреннего сгорания, такты 2—3 и 4—1 считаются изохорными процессами. Совершаемая на выходе мотора работа равна разности основных работ, которую производит газ над конкретным поршнем во время третьего такта и рабочего хода, включающий поршень на сжатие действующего вещества во время второго такта. Так как в указанном цикле используются принципы принудительного зажигания смеси, то происходит увеличение сжатия газа в 7—12 раз.

В другом цикле, под названием Стирлинг, также присутствуют два главных изохорных такта. Для его осуществления в устройстве добавлен мощный регенератор. Газ, проходя через наполнитель в одну сторону, отдаёт тепловую энергию от рабочего тела к регенератору, а при обратном движении возвращает его рабочей системе. Идеальный цикл Стирлинга достигает стопроцентной обратимости, а затем и тех же величин, что и цикл Карно.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Изменение внутренней энергии идеального газа в изопроцессах

Работа идеального газа

Геометрический смысл работы в термодинамике

История возникновения теории изохорного процесса

Первый закон термодинамики для изохорного процесса

Применение эффекта изохорного процесса

Не пропустите также: