Данная работа представляет собой
пример проведения урока по решению графических
задач по теме «Работа в термодинамике». Данный
метод позволяет во-первых, предоставить учащимся
возможность решить задачу у доски, не рискуя
получить неудовлетворительную отметку при
совершении ошибки, т.е. обеспечивается
психологический комфорт на уроке; во-вторых,
учащиеся, решающие задачу на своём рабочем месте,
могут сравнить своё решение с решением на доске и
участвовать в его обсуждении; в-третьих, учащиеся
могут решать задачи опережающими темпами (выбор
индивидуального образовательного маршрута);
в-четвёртых, учащиеся могут самостоятельно
выбрать себе домашнее задание, варьируя как
количество задач так и их сложность. В качестве
дидактического материала должен использоваться
раздаточный материал, содержащий как сами
задачи, так и алгоритм решения задач каждого
типа. При наличии проектирующих устройств на
экран проецируется алгоритм и задачи данного
типа. Важным фактом является то, что задачи
подобного типа являются не только
самостоятельными в данной теме, но и элементом,
лежащим в основе решения комбинированных задач
по теме «Газовые законы. Термодинамика», т.е.
задач части «С» ЕГЭ.
Исходными данными для решения задач
являются графики pV -, pT — и VT — зависимостей. В
качестве подготовки к данному уроку учащиеся
должны повторить способы определения изменения
параметров газа по графикам происходящих с ними
процессов. Урок строится по следующему
алгоритму: учитель объясняет принцип решения
задачи данного типа, затем учащиеся
самостоятельно решают предложенные задачи
данного типа. При этом должны соблюдаться
следующие принципы:
— каждая последующая задача решается у
доски другим учащимся;
— перед учащимися, решающими задачи на
рабочем месте, ставиться цель по возможности
решить задачу быстрее, чем решение появится на
доске, и сравнить решения;
— количество предлагаемых к решению
задач должно быть избыточным, чтобы каждый
учащийся мог в соответствии со своим темпом
решить максимально возможное количество задач;
— за одну — две минуты до окончания
решения задач данного типа учащимся может быть
предложено перерисовать себе графики нерешённых
задач в качестве домашнего задания.
Определение знака работы газа
(положительная, отрицательная).
Объяснение учителя.
Работа газа прямо пропорциональна
изменению его объёма, из чего следует, что знак
работы газа определяется знаком изменения его
объёма.
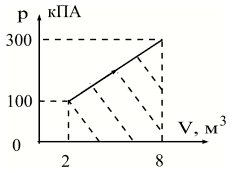
Учитель показывает решение на примере
изображённого на рис.1 графика. Из графика
очевидно вытекает, что объём газа увеличивается,
т.е. его изменение — положительная величина, из
чего следует, что работа газа положительна и газ
совершает работу над внешними силами. Это можно
записать символьным способом:
Аг~V
V^=> V>0=> Аг>0,
т.е. газ совершает работу над внешними силами.
Составить задачи для решения на уроке
не представляет трудности: среди них должны быть
графики как изо-, так и не изопроцессов; объём
газа должен быть задан в них как в явном так и в
неявном виде, объём газа должен как
увеличиваться, так и уменьшаться и оставаться
неизменным (работа газа равна 0, т.е. газ не
совершает работу). Количество решаемых на уроке
задач определяется степенью подготовленности
класса, т.е. скоростью их решения , и количеством
времени, отводимом учителем на решение задач
данного типа; количество предлагаемых для
решения задач должно быть избыточным. Подборка
возможных задач дана ниже.
Сравнение работы газа в различных
процессах.
Объяснение учителя.
Модуль работы газа численно равен
площади под графиком зависимости p(V). Поэтому
сравнение работ газа в различных процессах
сводится к сравнению площадей под графиком
процесса в осях pV.
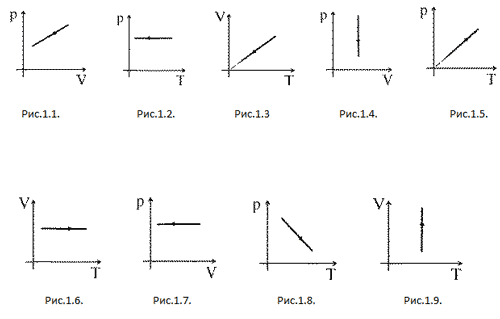
Учитель показывает решение на примере
изображённого на рисунке графика. Из графика
очевидно следует, что площадь под графиком
процесса 2-3 больше площади под графиком процесса
1-3 (заштрихованные площади). Из этого делается
вывод о том, что работа в процессе 2-3 больше
работы газа в процессе 1-2.
При решении задач учащимися они должны
обозначать и заштриховывать площади
соответствующих фигур под графиками.
При подборке задач необходимо
предусмотреть такие, в которых
— графики процессов представлены в
осях pV.
— работы газа в обоих процессах
положительны; отрицательны; работа газа в одном
из процессов положительна, в другом —
отрицательна; работа газа в одном из процессов
отрицательна, в другом — равна 0; работа газа в
одном из процессов положительна, в другом —
отрицательна, но они равны по модулю.
— при возможности полезно представить
графики процессов в осях VT или pT, провоцируя их на
ошибку делать вывод, сравнивая площади фигур под
графиками не тех зависимостей. При этом возможно
сравнить работы газа в процессах, если в одном из
них работа не совершается (изохорный процесс). В
противном случае необходимо перерисовать
графики процессов в осях pV (задача повышенного
уровня сложности).
В процессе решения задач учащимися
необходимо обратить внимание на то, что
сравниваются модули работы газа.
Количество предлагаемых учащимся для
решения задач как и в предыдущем случае
определяется учителем исходя из отводимого для
этого времени и степени подготовленности класса.
Подборка возможных задач дана ниже.
Определение работы газа в процессе,
изображённом на графике.
Объяснение учителя.
Модуль работы газа численно равен
площади под графиком зависимости p(V). Поэтому
решение задачи сводится к решению
геометрической задачи по определению площади
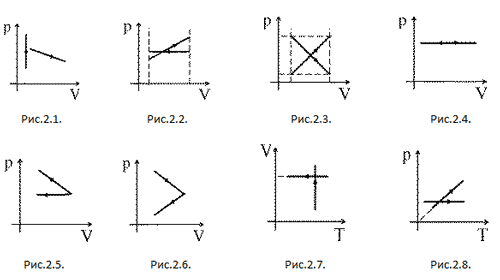
под графиком зависимости p(V). Рассмотрим пример
на рисунке 3.
рис. 3
Модуль работы газа численно равен
площади заштрихованной фигуры, т.е. трапеции. Из
геометрии известно, что площадь трапеции равна
произведению полусуммы её оснований на высоту.
Введём обозначения: p1 = 100 кПа; p2
= 300 кПа; V1 = 2 м3; V2 = 8 м3.
Введённые обозначения полезно нанести на график
для лучшего понимания учащимися вывода формулы
для решения задачи.
| Аг| = S (численно) => | Аг| =
0,5·( p1+ p2)·( V2 — V1) = 0,5·(100·103
+300·103)Па·( 8 — 2) м3 = 1,2·106 Дж.
Последующие задачи учащиеся решают
самостоятельно, в т.ч. и у доски.
При подборе задач необходимо
предусмотреть такие, чтобы в них присутствовали
графики:
— процессов с отрицательной работой
газа;
— нескольких последовательных
процессов, в которых в отдельных процессах
работа газа была как положительной, так и
отрицательной (и равной 0 — изохорные процессы);
— циклических процессов как с
положительной так и отрицательной работой газа
за цикл.
Полезно так же варьировать единицы
измерения давления и объёма газа. При наличии
учебного времени можно предложить графики
процессов, представленных в осях VT и pT, в этом
случае учащимся придётся сначала изобразить
процесс в осях pV с соответствующим расчётом
параметров состояний газа, а затем уже
определять работу газа.
В качестве домашнего задания учащимся
предлагается как минимум решить дома ещё раз
задачи, решённые в классе. В этом случае у них
появляется возможность самопроверки
правильности решения. Домашнее задание в большем
объёме регулируется учителем исходя из
поставленных учебных задач. При этом каждый
учащийся может выбрать для себя домашнее задание
требуемого объёма и уровня сложности.
Таким образом, реализация этого метода
позволяет
— создать комфортный психологический
климат на уроке;
— предоставить возможность большему,
чем при традиционных методах, количеству
учащихся решить задачу у доски под контролем
учителя;
— получить опыт проверки чужих решений,
сравнения со своим решением и при необходимости
его корректировке;
— каждому учащемуся выбрать свой
образовательный маршрут, регулируя как
количество решаемых на уроке задач, так и объём
домашнего задания по количеству и уровню
сложности выбираемых задач.
Ниже предложены возможные задачи для
использования на уроке. Очевидно, что учитель
может сделать свою подборку в соответствии с
уровнем подготовленности класса.
Задачи на определение знака работы.
Задачи на сравнение газа в различных
процессах.
Задачи на определение работы газа.
Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).
Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).
Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):
Рис. 3. Работа газа как площадь
к оглавлению ▴
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).
Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).
Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Условие задачи:
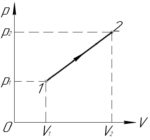
Задача №5.3.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(V_1=1) л, (V_2=2) л, (p_1=0,6 cdot 10^5) Па, (p_2=10^5) Па, (A-?)
Решение задачи:
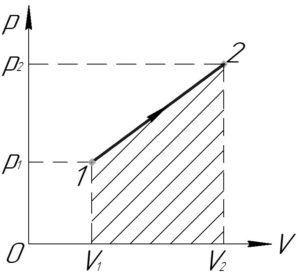
Фигура под графиком указанного процесса является трапецией, её площадь нужно находить как произведение полусуммы оснований на высоту, поэтому:
[A = frac{{left( {{p_1} + {p_2}} right)}}{2} cdot left( {{V_2} – {V_1}} right)]
Переведём объемы газа (V_1) и (V_2), приведённые в литрах, в систему СИ:
[1;л = 1 cdot {10^{ – 3}};м^3]
[2;л = 2 cdot {10^{ – 3}};м^3]
Посчитаем ответ к задаче:
[A = frac{{left( {0,6 cdot {{10}^5} + {{10}^5}} right)}}{2} cdot left( {2 cdot {{10}^{ – 3}} – 1 cdot {{10}^{ – 3}}} right) = 80;Дж]
Ответ: 80 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
5.3.23 Найти работу газа в процессе 1-2-3
5.3.25 Укажите, в каком из случаев работу внешних сил по изменению состояния идеального газа
5.4.1 Какова температура одноатомного идеального газа, если известно, что внутренняя энергия
Ранее мы достаточно плотно познакомились с процессами и методами работы с ними. Среди часто используемых способов работы с процессами выделяются два: уравнение Менделеева-Клапейрона (для описания состояния идеального газа) и первое начало термодинамики. Из нескольких друг за другом идущих разных процессов можно составить общий циклический процесс.
Круговой процесс (цикл) – составной термодинамический процесс, в результате совершения которого рабочее тело (газ) возвращается в исходное состояние. Таким образом, начальное и конечное состояние газа (давление газа , объём газа
и температура газа
) одинаковы. Попробуем изобразить такой процесс в координатах
(рис. 1).
Рис. 1. Примеры циклических процессов
Например, наш циклический процесс 1.1 состоит из двух изохор, двух изотерм, а процесс 1.2 — из двух изобар и двух изохор. Таким образом, исходя из текстовых условий любой задачи и знания общего вида изопроцессов (именно из них чаще всего составляется цикл), можно нарисовать рисунок.
Для энергетического описания процесса (или цикла) через первое начало термодинамики необходимо обдумать два вопроса:
- как изменяется внутренняя энергия газа (
)
- чему равна работа газа (
)
- где
Для циклов есть небольшие фишки, которые удобно использовать для убыстрения задачи.
Так, изменение внутренней энергии газа зависит только от изменения температуры, а т.к. в цикле начальное и конечное состояние газа одинаково, то изменение внутренней энергии идеального газа за цикл равно 0 ().
Рис. 2. Графическая интерпретация работы газа
Поиск работы для газа также можно несколько упростить. Попробуем в координатах нарисовать график изобарического процесса и найти работу газа (рис. 2). Пусть газ находится в состоянии (давление
и объём
), далее газ изобарически перевели в состояние 2 (давление
и объём
). Тогда по определению работы газа:
(1)
Геометрически (рис. 2), произведение давления на разность объёмов численно равна площади прямоугольника, ограниченного сверху прямой (процессом), а снизу осью. В целом, эту логику можно расширить на любые процессы, тогда работа газа численно равна площади под кривой в координатах .
Также в рамках школьной физики присутствует условное деление циклов на прямые и обратные:
Прямой цикл – круговой, в котором рабочее тело совершает положительную работу за счёт сообщённой ему теплоты.
Обратный цикл — круговой, в котором рабочее тело совершает отрицательную работу.
Анализируя (1) вопрос о положительной и отрицательной работе, сводится к вопросу о соотношении между начальным и конечным объёмами, если:
Для графиков можно использовать следующую логику: в случае, если площадь под графиком расширения газа больше соответствующей площади для сжатия, значит цикл — прямой (рис. 3), если наоборот — обратный (рис. 4).
Рис. 3. Прямой циклический процесс
Рис. 4. Обратный циклический процесс
Таким образом, разница в прямом и обратном цикле может быть в очерёдности процессов. Так, прямой процесс, в нашем примере, — это 1-2-3-4-1, а обратный — 1-4-3-2-1.
Вывод: в задачах на циклические процессы нужно быть очень внимательным при прочтении, т.к. часть слов будет иметь глубокий физический смысл. Лучше всего процессы в таких задачах прорисовывать на графиках в координатах . Если график уже есть, то это к лучшему. Определяемся с конкретными изопроцессами, заданными в задаче, и используем это знание или через уравнение Менделеева-Клапейрона, или через первое начало термодинамики.
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505

Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
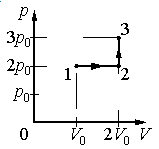
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.1k