— простые задачи на скорость, время и расстояние;
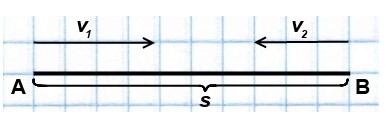
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.
Скорость, время и расстояние: определения, обозначения, формулы
скорость = расстояние: время — формула нахождения скорости;
время = расстояние: скорость — формула нахождения времени;
расстояние = скорость · время — формула нахождения расстояния.
Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.
На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:
1.Конвертер единиц измерения скорости
2.Конвертер единиц измерения времени
3.Конвертер единиц измерения расстояния (длины)
Примеры простых задач.
Задача 1.
Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.
Задача 2.
Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.
Задача 3.
Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.
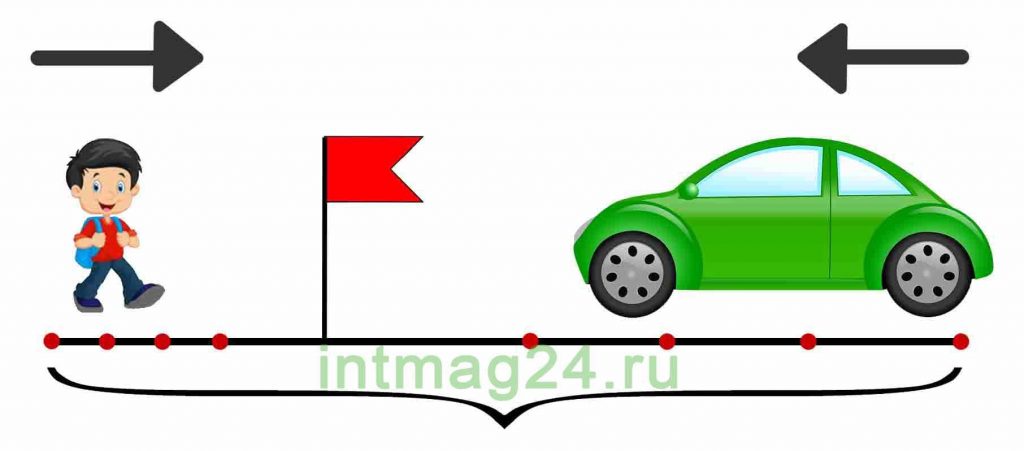
Задачи на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Задача 4.
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.
Задача 5.
Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.
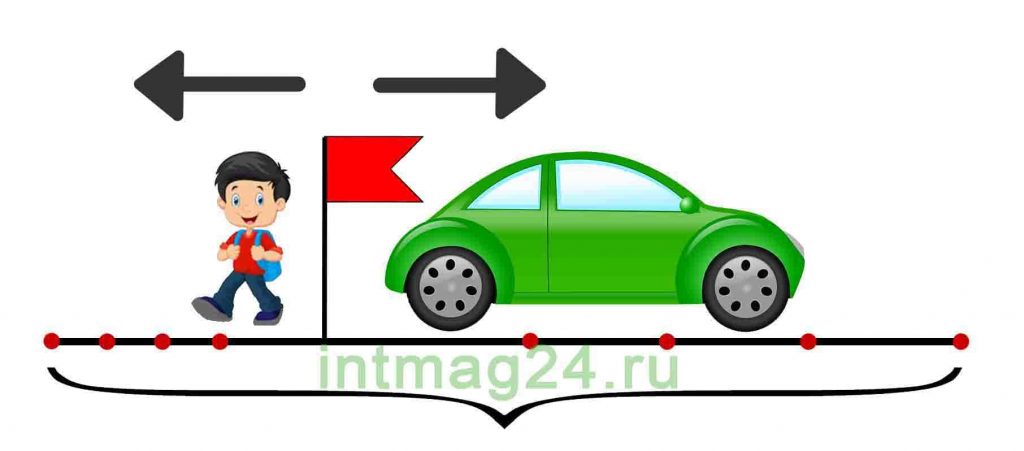
Задачи на движение в противоположных направлениях
В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Задача 6.
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 7.
Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
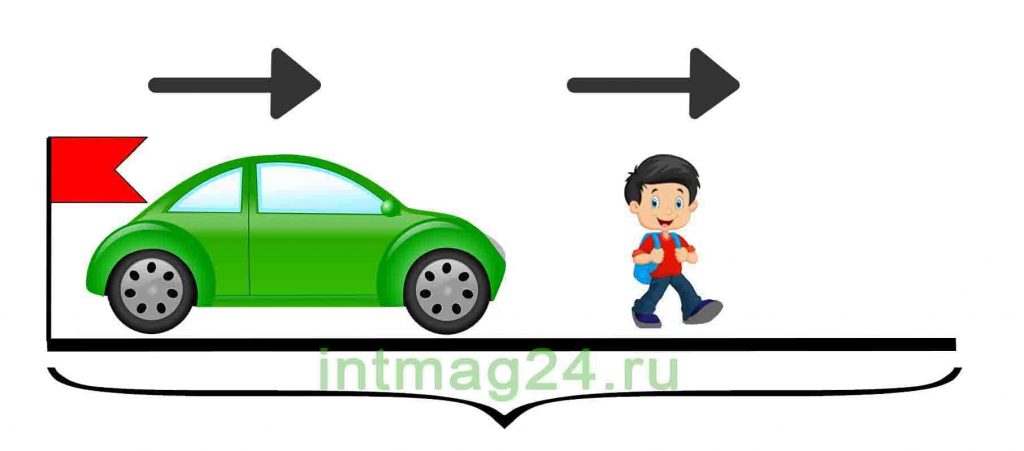
Задачи на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.
Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.
Задача 8.
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 9.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 10.
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 11.
Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.
Итак, для решения задач на движение:
- Основная формула:S=ν*t;
- Нужно сделать чертеж, который поможет определить тип задачи.
- Все цифры нужно привести в единые единицы измерения: длина и время
Заключение.
Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов.
Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте edu.intmag24.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.
Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.
На чтение 10 мин. Просмотров 6.7k.
Вычислить скорость, время и расстояние часто бывает необходимо в повседневной жизни, когда мы рассчитываем время на дорогу. Все эти величины (время, расстояние и скорость) связаны между собой математической формулой и зная две из них всегда можно найти третью. Мы с вами рассмотрим, что понимается под этими величинами, как их найти, решим несколько задач.
Скорость, время и расстояние — это ключевые параметры при решении задач на движение. Эти задачи есть и в ЕГЭ и в ОГЭ по математике. Сегодня мы подробнее остановимся на этих величинах.
Расстояние
Расстояние — это физическая величина, означающая длину между двумя объектами. Расстояние обозначается буквой S и измеряется в единицах длины: метрах. Метр — это международно-принятая единица измерения длины. Однако встречаются и другие единицы длины — километр, сантиметр, миллиметр. В этом случае целесообразно перевести единицы длины в международную систему единиц (СИ).
Например: расстояние от Земли до Солнца равно 149 597 870 700 метров.
Расстояние связано со скоростью и временем:
S=v cdot t
Вот тут таблица длин и их перевода в международную систему единиц — то есть в метры.
| Единицы длины | СИ |
| 1 сантиметр | 0,01 м |
| 1 километр | 1000 м |
| 1 дециметр | 0,1 м |
| 1 миллиметр | 0,001 м |
| 1 микрометр | 1·10-6 м |
| 1 миля | 1609,34 м |
| 1 фут | 0,3048 м |
| 1 ярд | 0,9144 м |
| 1 дюйм | 0,0254 м |
| 1 морская миля | 1852 м |
Время
Время — это физическая величина, которая обозначает непрерывное и необратимое (возможно) движение от прошлого к будущему через настоящее. Это фундаментальная физическая величина, единица измерения времени — секунда. Однако, в задачах могут использоваться и другие единицы времени — часы, минуты, дни.
Время можно найти по формуле:
t=frac{S}{v}
Ученые о времени
По словам греческого философа Парменида (ок. 450 г. до н.э.), время и движение были иллюзиями. Его ученик Зенон Элейский разработал два знаменитых парадокса: «Ахиллес и черепаха» и «Парадокс летящей стрелы», чтобы доказать его утверждения. Платон, живший на пару поколений позже, считал, что время создано вместе со вселенной и существует независимо. Он рассматривал время как пустой контейнер, который можно заполнить движущимися вещами и событиями. Его ученик Аристотель считал, что время не существует независимо от событий, но время есть изменение и движение.
Аристотель пришел к выводу, что время не состоит из последовательных неделимых моментов «сейчас», как пытался сказать Зенон с помощью своего парадокса стрелы. Согласно Аристотелю, не существует серии моментов «сейчас», потому что такие моменты не могли бы исчезнуть в течение их собственной длительности или в следующий момент «сейчас». Исааку Ньютону (1642–1726) время понадобилось в качестве переменной в его уравнениях, и он начал думать о времени с научной точки зрения. Ньютон поддерживал идею Платона о независимости времени. Он разделил время на абсолютное (математическое) время и относительное (обычное) время.
Абсолютное время, или продолжительность, является реальным и математическим, и оно течет неуклонно, независимо от чего-либо внешнего. Относительное время кажущееся и является внешней мерой длительности, которая может быть обнаружена органами чувств с помощью движения, которое может быть точным или неточным.
Готфрид Лейбниц (1646–1716) был согласен с Аристотелем и думал, что без событий и перемен не было бы времени. Физик- теоретик Ли Смолин писал в 2010 году, что исследования квантовой гравитации подтверждают, что четырехмерное пространство-время имеет смысл только в том случае, если время реально, фундаментально и даже является единственным аспектом реальности, который мы непосредственно ощущаем.
Скорость
Скорость обозначается буквой — это физическая величина, которая обозначает какое расстояние проходит объект в единицу времени. Единица измерения скорости — м/с. Однако, встречаются также и км/ч и см/с (эти измерения не входят в международную систему единиц измерения). Скорость показывает как быстро изменяется расстояние во времени.
Например, выражение 9 м/с означает, что тело за 1 секунду проходит 9 метров. То есть за 1 секунду 9 метров, за 2 секунду еще 9 метров, итого за 2 секунду — 18 метров. В курсе школьной математики мы считаем, что скорость равномерная во времени. То есть тело за равные промежутки времени проходит равные расстояния. То есть 9 м/с означает 9 метров в любую из секунд движения тела. Однако, в реальности движение бывает равномерное и неравномерное. Мы не рассматриваем неравномерное движение в курсе математики (1-6 класс), однако в курсе алгебры элементы кинематики с неравномерным движением рассматриваются.
Еще примеры: скорость 100 км/ч — это прохождение расстояния в 100 километров за 1 час.
Формула скорости
Скорость можно найти через расстояние и время по формуле:
v=frac{S}{t}
Средняя скорость
Если движение тела можно разбить на несколько участков и в пределах каждого участка скорость тела не меняется, то целесообразно говорить о средней скорости.
Формула средней скорости:
v=frac{S_{весь ; путь}}{t_{всё ; время}}=frac{S_1+S_2+…+ S_n}{t_1+t_2+…+ t_n}
То есть средняя скорость это отношение всего пути, ко всему времени.
Скорости сближения и удаления
Понятие скорости ученики изучают еще в 4 классе, а далее это понятие расширяется и уточняется. Вводятся такие понятия как скорость сближения и скорость удаления. Не все педагоги используют эти понятия в своей работе, поскольку эти понятия можно использовать только при решении небольшого класса задач на движение и они ограничивают решение задач и другими условиями (например, если тела удаляются или сближаются не по одной прямой, а по перпендикулярным прямым). И все же, давайте мы уточним, о чем вообще идет речь.
Скорость удаления
Если два тела удаляются друг от друга, двигаясь по одной прямой, то в таких случаях говорят о скорости удаления. То есть скорость удаления характеризует расстояние, которое увеличивается по мере удаления двух тел в единицу времени.
Допустим есть два пешехода, которые удаляются друг от друга, первый пешеход удаляется со скоростью 3 км/ч, а второй пешеход со скоростью 4 км/ч. Тогда скорость удаления будет:
3+4=7 км/ч.
Действительно, расстояние, пройденное первым пешеходом за один час будет 3 километра, а расстояние, пройденное вторым пешеходом за то же время будет 4 километра. Тогда при удалении пешеходов друг от друга расстояние между ними увеличивается на 7 километров в каждый час или наши пешеходы удаляются со скоростью 7 км/ч. Мы должны сложить скорости объектов.
Формула скорости удаления:
v_{удаления}=v_1+v_2
где
— скорость одного тела,
— скорость другого тела.
Напомним, что это понятие можно использовать только если тела двигаются в разных направлениях, располагаемых на одной прямой.
Скорость сближения двух тел
Аналогично, рассмотрим ситуацию, если два пешехода двигаются навстречу друг к другу. Один пешеход за один час проходит расстояние 2 км, а второй пешеход за то же время проходит 5 км.
Значит, расстояние между ними будем уменьшаться со скоростью 5+2 = 7 км/ч.
Формула скорости сближения:
v_{сближения}=v_1+v_2
где
— скорость одного тела,
— скорость другого тела.
Если один пешеход догоняет другого. То скорость сближения при движении в одном направлении можно определить, если вычесть из большей скорости меньшую.
То есть, если у нас второго пешехода (=3км/ч) догоняет первый пешеход (
=5 км/ч), то скорость их сближения будет 2 км/ч:
Формула скорости сближения при движении вдогонку:
v_{сближения}=v_1-v_2
где
— скорость одного тела,
— скорость другого тела. При этом
Таблица «скорость, время, расстояние» при решении задач на движение
При решении задач на движение очень удобно пользоваться такой таблицей, в которой три столбца с данными по скорости, времени движения тел и расстоянию, которое они проходят. Эта таблица, кстати помогает легко запомнить формулы скорости, времени и расстояния, если представить что первый столбец — это первый множитель, второй столбец — второй множитель, а третий столбец — произведение.
| Скорость, v, м/с | Время, t, с | Расстояние, S, м |
Простой пример, найти скорость велосипедиста, если за 5 часов он прошел 45 километров.
Составляем таблицу и записываем в нее данные:
| Скорость, v, км/ч | Время, t, ч | Расстояние, S, км |
| ? | 5 | 45 |
Теперь видно, что неизвестна скорость в первом столбце, значит, неизвестен первый множитель. Чтобы определить неизвестный множитель надо произведение разделить на известный множитель: = 45/5 = 9 км/ч.
Важно! В задачах все единицы измерения должны быть приведены либо к международной системе единиц (метр, секунда, м/с) либо к одним единицам измерения (то есть если в задаче есть и м/с и км/ч можно привести всё либо к м/с (тогда и время в секундах и расстояние в метрах), либо к км/ч (тогда и время в часах будет и расстояние в километрах))
Рассмотрим теперь некоторые примеры решения задач
Примеры задач на движение
Задача 1
Школьник идет домой со скоростью 2 км/ч. Расстояние от школы до дома 1 км. За какое время школьник дойдет до дома?
Решение:
Найдем время по формуле: displaystyle t=frac{S}{v}=frac{1}{2}ч.
Школьник дойдет до дома за полчаса.
Ответ: 0,5 ч.
Задача 2
Автомобилист и велосипедист выехали в город из деревни одновременно. Скорость автомобилиста 50 км/ч. Расстояние до города 100 км. Какова скорость велосипедиста, если известно, что он прибыл в город на 8 часов позже автомобилиста?
Решение: Составим таблицу
| Скорость, v, км/ч | Время, t, ч | Расстояние, S, км | |
| Автомобилист | 50 | 100/50 | 100 |
| Велосипедист | x | 100/x | 100 |
Пусть скорость велосипедиста x. В таблице мы сразу смогли написать соотношения для времени движения. По условию задачи дано, что велосипедист прибыл в город на 8 часов позже автомобилиста. Запишем это:
displaystyle frac{100}{x}-frac{100}{50}=8
Мы отнимаем от времени, которое потратил велосипедист (он же потратил больше времени) время, которое потратил автомобилист и получаем 8 часов.
Решим полученное уравнение.
displaystyle frac{100}{x}-2=8
displaystyle frac{100}{x}=10
x=10
Ответ: 10 км/ч
Задача 3
Стрела пролетает 180 метров за 0,05 минуты. Найдите ее скорость.
Решение: прежде чем решать задачу, переведем все единицы в одну систему единиц. Минуты переведем в секунды.
В одной минуте 60 секунд. Значит, чтобы узнать сколько секунд в 0,05 минутах, умножим 0,05 на 60, получим:
0,05 cdot 60=3 c.
Тогда displaystyle v= frac{180}{3}=60 м/с.
Ответ: 60 м/с
Задача 4
Турист прошел лесной участок длиной 10 км со скоростью 5 км/ч, а затем шел по полю 20 км, со скоростью 4 км/ч. Какова средняя скорость туриста?
Решение:
Определим весь путь который прошел турист:
displaystyle S_{весь ; путь}=S_1+S_2=10+20=30 км.
Для прохождения лесного участка турист потратил: displaystyle t_1= frac{S_1}{v_1}=frac{10}{5}=2ч, а на второй участок времени ушло: displaystyle t_2= frac{S_2}{v_2}=frac{20}{4}=5ч
Все время: displaystyle t_{всё ; время}=t_1+t_2=2+5=7ч
Тогда найдем среднюю скорость:
displaystyle v_{ср}= frac{S_{весь ; путь}}{t_{всё ; время}}=frac{30}{7}=4 frac{2}{7} км/ч.
Ответ: displaystyle v_{ср}=4 frac{2}{7}
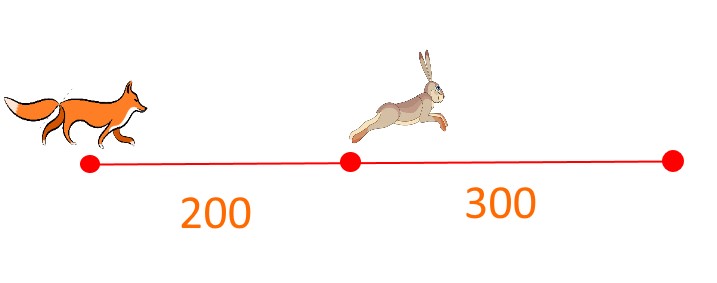
Задача 5
Лиса гонится за зайцем. Скорость лисы 20 м/с, а скорость зайца 15 м/с. Догонит ли лиса зайца, если заяц находится на расстоянии 300 метров от безопасного места, а лиса находится на расстоянии 200 метров от зайца?
Решение:
Заяц добежит до норы за displaystyle t= frac{300}{15}=20 секунд.
Лиса же за 20 секунд пробежит расстояние displaystyle S= 20 cdot 20=400 метров.
Лиса не догонит зайца.
Действительно, скорость сближения лисы и зайца:
displaystyle v=v_{лисы}-v_{зайца}=20-15=5 м/с
То есть, чтобы преодолеть расстояние 200 метров, которое изначально существует между лисой и зайцем, лисе понадобиться displaystyle t=frac{200}{5}=40 с
Заяц же уже 20 секунд будет в безопасном месте.
Ответ: лиса зайца не догонит.
При решении задач на движение, главное найти три ключевые величины: расстояние, время и скорость. Для этих величин можно записать один из законов движения:
(S=v*t)
Сегодня в этой статье мы познакомимся с задачами на движение по течению и против течения реки. Также рассмотрим задачи на сближение и удаление. Также стоит помнить, что в таких задачах данные величины нужно приводить к единой системе единиц.
. Катер плыл против течения реки (120) км, назад он плыл, затратив на путь на (2) часа меньше. Найдите скорость катера без течения реки, если скорость течения (1) км/час.
(frac{120}{x+1}+2=frac{120}{x-1})
(frac{120}{x-1}+2(x-1)(x+1)=frac{120}{x+1}) (x) не равно (-1) и (+1) так как задача не будет иметь решения.
(120x-120+2x^2-2=120x+120)
(2x^2=242)
(x^2=121)
(x=11) км/час
Ответ: (11) км/час.
. Человек плывет со скоростью (5) км/ч. Если скорость течения равна (1) км/ч, то ему требуется (1) час, чтобы плыть к месту и вернуться обратно. Найдите расстояние до этого места.
Пусть расстояние х км и скорость по течению будет равна (5+1=6) км/ч. Скорость против течения тогда (5-1=4) км /ч. Составим уравнение (frac{x}{6}+frac{x}{4}=1), так как (s/v=t).
Домножим обе части уравнения на (12) :
(2x+3x=12)
Решим полученное уравнение:
(x=frac{12}{5}=2,4 ) (км.)
. За один час лодка проходит (11) км по течению и (5) км против течения. Найтите скорость лодки в стоячей воде.
Решение.
- (frac{1}{2}(a+b)=frac{1}{2}(11+5)=frac{1}{2}(16)=8) (км/ч.)
. Если Максим плывет (15) км против течения за (3) часа и за это же время — (21) км по течению. Найтите скорость течения.
Решение.
cкорость вверх по течению равна (frac{15}{3}=5 ) км/ч;
cкорость вниз по течению (frac{21}{3}) км/ч = (7) км /ч;
cостовляем уравнение и находим скорость течения (frac{1}{2}(7-5)) км / ч = (1) (км/ч.)
. За один час лодка проходит (11) км по течению и (5) км против него. Найтите скорость лодки в неподвижной воде.
Решение.
- (frac{1}{2}(a+b)) = (frac{1}{2}(11+5)=frac{1}{2}16=8 ) (км/ч.)
. Вика плывет со скоростью (4) км/ч. Если скорость течения равна (1) км/ч и ей требуется (1) час, чтобы плыть к месту и вернуться обратно. Найдите расстояние до этого места.
Решение.
Пусть расстояние (x) км.
Скорость Вики по течению равна (4+1=5) км/ч.
Скорость Вики против течения равна (4-1=3) км/ч.
Составим уравнение: (frac{x}{5}+frac{x}{3}=1) так как (s:v=t).
(3X+5x=15)
= >(8x=15=1,875) (км.)
Ответ: (1,875).
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n
где v1, v2, v3, vn – значения скоростей объекта на отдельных участках пути S,
n – количество этих участков,
vср – средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
vср=(S1+S2+…+Sn)/t,
где vср – средняя скорость объекта на всем протяжении пути,
S1, S2, Sn – отдельные неравномерные участки всего пути,
t – общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
vср=S/(t1+t2+…+tn),
где S – общее пройденное расстояние,
t1, t2, tn – время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn,
где S1/t1, S2/t2, Sn/tn – формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Хорошее приложение. Спасибо
- reply
Спасибо гигантское, вы меня выручили
- reply
С какой скоростью должен ехать автомобиль если он за 8 секунд проехал 300 метров
- reply
Один пешеход идёт со скоростью 13км/ч а другой 18км/ч их встреча произойдет через восемь часов. Сколько километров они преодолели до своей встречи?
- reply
13*8+18*8= 248 км, только 18 км/час это почти мировой рекорд при забеге на 20 км
- reply
Задача поезд едет 95км ч а машина 140км ч а расстояние между ними 1535 км через сколько времени они встретятся
- reply
Вы тооооп.Спасибо за прекрасный сайт!!!!
- reply
в описании к калькулятору добавьте, что из-за особенностей Javascript он не принимает «,» даже не представляю сколько людей погорело у вас тут.
- reply
Administration
370 дн. назад
Спасибо.
Поддержку «,» добавили.
- reply
Два пешехода вышли навстречу друг другу. Скорость первого составляет 3 м/мин, а второго — 4 м/мин. Через
сколько минут они встретятся, если расстояние между ними 1680 метров?
- reply
Медвежат отвезли за 600 км от населенного пункта. Через 18 дней (432часа) они вернулись в посёлок. Вопрос: Это реально? И с какой скоростью они могли передвигаться в сутки?
- reply
За какое время пройдёт машина расстояние 10 метров со скоростью 170км/ч
- reply
задача.1 трактор ехал со скоростью 36 км.в час .2 трактор _32 км в час между ними .растояние 136км.нужно найти время когда встретятся.
- reply
От города A до города B расстояние 40 км. Два велосипедиста выехали из A и B навстречу друг другу, один со скоростью 10 км/ч, а другой — 15 км/ч. Муха вылетела с первым из A со скоростью 100 км/ч, долетела до второго, села ему на лоб и полетела обратно к первому, села ему на лоб, вернулась ко второму и так далее, пока они не столкнулись лбами и не раздавили ими муху. Сколько километров пролетела муха?
- reply
машина едет со скоростью 85 км в час ,за сколько минут проедет машина 78 км
- reply
Если пешеход вышел в деревню со скоростью 4.8 км/ч,возвращался со скоростью 6 км/ч и вернулся на час раньше. Какое расстояние от села до деревни?
- reply
Если пешеход вышел в деревню со скоростью 4.8 км/ч,возвращался со скоростью 6 км/ч и вернулся на час раньше. Какое расстояние от села до деревни?
- reply
Скорость автомобиля 110 кмч.
а) за какое время он проедет 33 км
б) какое расстояние он проедет за 1,5 ч
- reply
Расстояние в 3 км и скорости 30км/ч выдаёт 6 часов пути?!!
- reply
0.1 часа или 6 минут. Там так написано
- reply
Если легковая машина едет 70 км в час то сколько она проедет за 1 час 48 минут
- reply