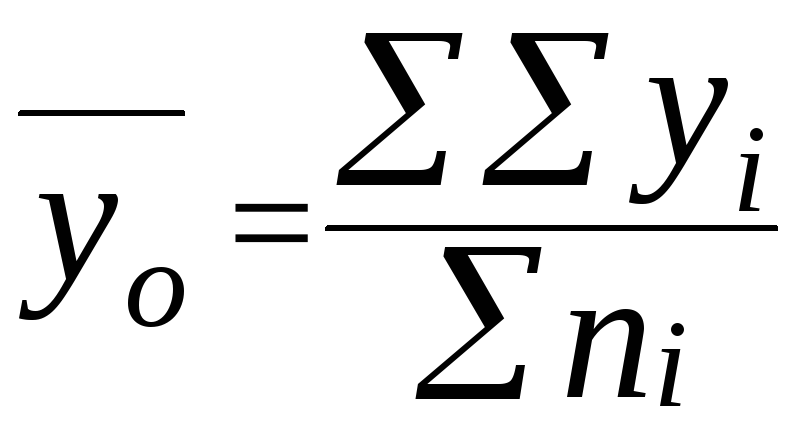Тема: Ряды динамики.
Ряд изменяющихся
во времени и расположенных в хронологической
последовательности значений статистических
показателей представляют собой временной
или динамический ряд.
В каждом ряду
динамики имеются 2 основных
элемента:
-
период времени,
за который или по состоянию на который
приводятся цифровые значения (показатель
времени t); -
числовые значения
того или иного показателя, называемые
уровнями развития изучаемого явления
(уровни ряда у).
В качестве показателя
времени в рядах динамики выступают либо
определённые даты (моменты времени),
либо отдельные периоды (годы, месяцы,
кварталы и т.д.). В связи с этим ряды
динамики можно разделить на моментные
и интервальные.
Основным
условием для получения правильных
выводов при анализе рядов динамики и
прогнозирование его уровней является
сопоставимость уровней ряда между
собой. Статистические
данные должны быть сопоставимы:
по
кругу
охватываемых объектов, времени
регистрации, территории, идеологии
расчета и ценам.
Основные показатели
анализа ряда динамики.
Показатели анализа
ряда динамики могут рассчитываться на
постоянной и переменной базах сравнения.
При этом принято называть сравниваемый
уровень отчётным, а уровень, с которым
производится сравнение – базисным.
Для расчёта
показателей на постоянной базе каждый
уровень сравнивается с одним и тем же
базисным уровнем. Рассчитанные при этом
показатели называется базисными.
Для расчёта показателей на переменной
базе каждый последующий уровень
сравнивается с предыдущим. Показатели
называют цепными.
-
Абсолютный
прирост (абсолютное изменение).
Определяется как
разность между двумя уровнями динамического
ряда и показывает, на сколько единиц
данный уровень ряда превышает уровень
другого периода. Абсолютный прирост
может иметь положительный или отрицательный
знак.
а)
базисный
=
,
б) цепной
=
,
где уi—
уровень сравниваемого периода;
y
i
-1 – уровень
предшествующего периода;
y0
– уровень базисного периода.
-
Темп роста.
Определяется как
отношение двух сравниваемых уровней и
показывает, во сколько раз данный уровень
превышает уровень базисного периода.
а) базисный
=
·100%
б) цепной
=
·100%
-
Темп прироста
(или темп
сокращения).
Характеризует
относительную скорость изменения уровня
ряда в единицу времени.
Можно рассчитать
2 способами:
1).Как
отношение абсолютного прироста к уровню:
а) базисный
=
·100%=
·100%
б) цепной
=
·100%=
·100%
2).Как
разность между темпом роста и 100%.
=
-100%
4.Темп наращивания (пункт роста).
Рассчитывается
делением цепных абсолютных приростов
на уровень, принятый за постоянную базу
сравнения.
=
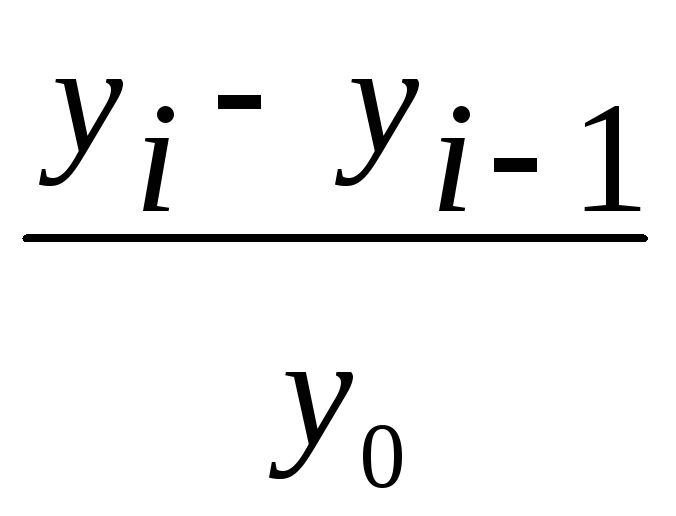
·100%
5.Абсолютное значение одного процента прироста.
Чтобы
знать, что скрывается за каждым процентом
прироста, рассчитывается абсолютное
значение 1% прироста как
отношение абсолютного прироста уровня
за интервал времени к темпу прироста
за тот же промежуток времени:

Средние показатели
по рядам динамики.
Для обобщения
характеристики динамики исследуемого
явления за ряд периодов определяют
различного рода средние показатели.
Рассмотрим 2
категории:
-
Средние показатели
изменения уровня ряда:
а)
средний абсолютный прирост (средняя
скорость роста).


где n-
количество уровней ряда
уn—
самое последнее значение уровня ряда;
у1—
самое первое значение.
б) средний
темп роста
или
-
Средние
уровни ряда
зависят от вида временного ряда.
Статистическое
изучение сезонных колебаний.
Сезонным
колебаниям свойственны более или менее
устойчивые изменения уровней ряда на
протяжении изучаемого периода: из года
в год в определенные месяцы уровень
явления повышается, а в другие —
снижается.
Сезонные колебания
чаще всего происходят в добывающих и
перерабатывающих отраслях –
сельскохозяйственной, рыбной, лесной,
а также в строительстве, транспорте,
торговле, туризме и т.д.
Способы
определения индексов сезонности
различны, они зависят, прежде всего, от
характера общей тенденции ряда динамики.
Итак,
индексами сезонности
являются
процентные отношения фактических
(эмпирических) внутригрупповых уровней
к теоретическим расчётным уровням,
выступающих в качестве базы сравнения.
Их вычисляют по данным за несколько лет
(не менее трёх), распределённым по
месяцам.
Для каждого месяца
рассчитывается средняя величина уровня,
а затем рассчитывается среднемесячный
уровень для всего ряда, %:
=
*100%,
где

осредненные
эмпирические уровни ряда по одноименным
периодам (месяцам или кварталам);

— общий
средний уровень ряда.
Для наглядного
представления сезонной волны индексы
сезонности изображаются в виде графиков.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —— | —— | 100.0 | 100.0 | —— | —— |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Гражданское право — работа с недвижимостью. договорная работа, наследственное право, банкротство.
Важнейшим показателем эффективности производства в анализе финансовой ситуации компании является показатель темпа роста. Поговорим об особенностях его расчета.
Как рассчитать темп роста: формула
Что называют снижением темпа роста цен?
Подробнее
Этот термин показывает изменение значения любого экономического или статистического показателя в текущем периоде к его начальному значению (являющемуся базовым) за определенный временной промежуток. Измеряется он в процентах или коэффициентах.
Например, при сравнении объема выпуска товаров на конец года (допустим, в значении 100000 руб.) к показателю объема на начало года (70000 руб.) темп роста находят отношением конечного значения к начальному: 100000 / 70000 = 1,428. Индекс роста в примере составил 1,429. Это означает, что на конец года объем выпуска составил 142,9%.
Как рассчитать темп роста в процентах — формула:
ТР = Пт / Пб х 100%,
где Пк и Пб – показатели значений текущего и базового периодов.
Узнайте, может ли темп роста быть отрицательной величиной.
Темп роста показывает интенсивность изменений какого-либо процесса по отношению к его начальному (базовому) значению. Результат вычислений – один из трех вариантов:
-
ТР больше 100%, следовательно, конечное значение возросло в сравнении с начальным, т.е. налицо рост показателя;
-
ТР = 100%, т.е. изменений ни в большую, ни в меньшую сторону не произошло – показатель остался на прежнем уровне;
-
ТР меньше 100%, значит, анализируемый показатель снизился к началу периода.
Приведем примеры, как рассчитать темп роста в процентах по каждому варианту расчета, объединив исходные данные в таблицу:
|
Объем выпуска в тыс. руб. |
Расчет (Пт / Пб х 100%) |
|
|
2017 (Пб) |
2018 (Пт) |
|
|
600 |
800 |
133,3% |
|
600 |
600 |
100% |
|
600 |
400 |
66,7% |
Такой темп роста называют базисным, поскольку база сравнения по периодам остается неизменной – показатель на начало периода. Если же сравнительная база изменяется, а темп роста вычисляют отношением текущего значения к предыдущему (а не базисному), то этот показатель будет цепным.
Узнайте, чем отличается темп роста от темпа прироста.
Как рассчитать цепные темпы роста
Рассмотрим пример расчета базисного и цепного темпов роста:
|
Период |
Объем в тыс.руб. |
Темп роста в % |
|
|
базисный |
цепной |
||
|
1 кв. |
300 |
100 |
— |
|
2 кв. |
310 |
103,3 (310 / 300) |
103,3 (310 / 300) |
|
3 кв. |
280 |
93,3 (280 / 300) |
90,3 (280 / 310) |
|
4 кв. |
360 |
120 (360 / 300) |
128,6 (360 / 280) |
Цепные темпы роста характеризуют насыщенность изменения уровней от квартала к кварталу, базисные же отражают ее в целом за весь временной интервал (показатель 1 квартала – база сравнения).
Сравнивая показатели в приведенном примере, можно отметить, что ряд значений, рассчитанных к началу периода, имеет меньшую амплитуду колебаний, чем цепные показатели, вычисления которых привязаны не к началу года, а к каждому предшествующему кварталу.
Как рассчитать темпы прироста
Кроме расчета темпов роста, принято высчитывать и темпы прироста. Эти значения также бывают базисными и цепными. Базисный прирост определяют как отношение разности показателей текущего и базового периодов к значению базового периода по формуле:
∆ ТР = (Птек – Пбаз) / Пбаз х 100%
Цепной прирост рассчитывают как разность между текущим и предыдущим показателями, деленную на темп роста предыдущего периода:
∆ ТР = (Птек – Ппр.п) / Ппр. п х 100%.
Более простым способом расчета является формула: ∆ ТР = ТР – 100%, где расчетные показатели темпа роста уменьшаются на 100%, т. е. исходную величину. Показатель темпа прироста в отличие от значений темпа роста может иметь отрицательное значение, поскольку темп роста (или снижения) показывает динамику изменений показателя, а темп прироста говорит о том, какой характер они носят.
Продолжая пример, рассчитаем приросты объемов в рассматриваемых периодах:
|
Период |
Темпы прироста |
|
|
базисные |
цепные |
|
|
1 кв. |
— |
— |
|
2 кв. |
3,3% (103,3 – 100) или ((310 – 300) / 300 х 100) |
3,3% (103,3 – 100) или ((310 – 300) / 300 х 100) |
|
3 кв. |
— 6,7% (93,3 – 100) или ((280 – 300) / 300 х 100) |
-9,7% (90,3 – 100) или ((280 – 310) / 310 х 100) |
|
4 кв. |
20% (120 – 100) или (( 360 – 300) / 300 х 100) |
28,6% (128,6 – 100) или ((360 – 280) / 280 х 100) |
Анализируя результаты вычислений, экономист может сделать вывод:
-
Прирост объемов наблюдался во 2-м и 4-м кварталах, причем во 2-м он был наименьшим (3,3%). В 3-м квартале объем выпуска сократился на 6,7% в сравнении с показателями начала года;
-
Цепные темпы прироста обнаружили более глубокие колебания: объемы 3-го квартала снизились по отношению к показателям 2-го на 9,7%. Зато выпуск товаров в 4-м квартале вырос почти на треть в сравнении с итогами 3-го квартала. Столь существенные изменения в объемах производства могут свидетельствовать о сезонности выпускаемых продуктов, перебоях в снабжении необходимым сырьем или других причинах, которые исследует аналитик.
Как рассчитать средний темп роста
Средний темп роста – обобщающая характеристика уровня изменений. Расчет средних темпов роста и прироста также разграничивают на базисные и цепные. Для определения среднего темпа роста расчетные показатели по периодам складывают и делят на количество периодов. Таким же образом находят и средние темпы приростов. Вернемся к предыдущему примеру, рассчитав средние значения базисных темпов роста и прироста, а также аналогичных цепных показателей.
|
Показатель |
Значение в % |
Расчет |
|
Средний темп роста (базисный) |
105,5 |
(103,3 + 93,3 + 120) / 3 |
|
Средний темп прироста (базисный) |
5,5 |
(3,3 – 6,7 + 20) / 3 |
|
Средний темп роста (цепной) |
107,4 |
(103,3 + 90,3 + 128,6) / 3 |
|
Средний темп прироста (цепной) |
7,4 |
(3,3 – 9,7 + 28,6) / 3 |
Полученные цифры свидетельствуют о том, что в среднем с начала года объемы выпуска выросли на 5,5%, а в поквартальной привязке рост составил 7,4%.
Читайте также: Экспресс-анализ финансового состояния предприятия

Специализация: Гражданское право — работа с недвижимостью. договорная работа, наследственное право, банкротство.
Окончила в 2005 г. Тверской государственный университет, юридический факультет, специальность-юриспруденция.
Юрист в сфере недвижимости:составление договоров, регистрация в Росреестре прав и сделок,оформление наследственных прав,
сопровождение сделок с недвижимым имуществом,судебный опыт по делам,связанным с признанием прав на недвижимость.
Имеется опыт работы помощником арбитражного управляющего.