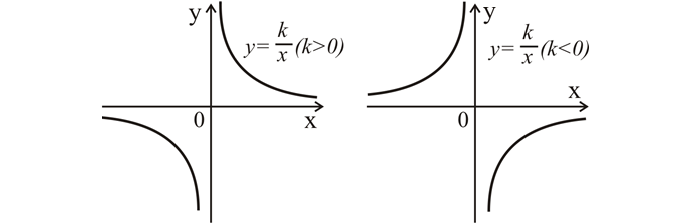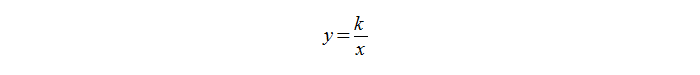Прямая и обратная пропорциональность
- Прямая пропорциональность
- Формула прямой пропорциональности
- Обратная пропорциональность
- Формула обратной пропорциональности
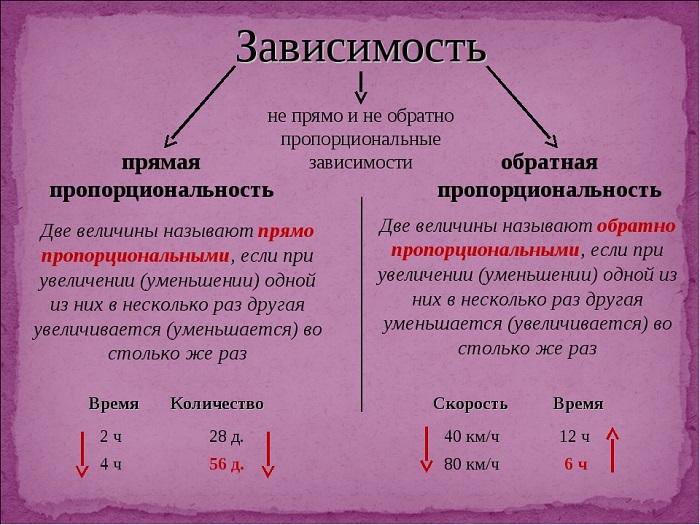
Пропорциональность — это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.
Пропорциональность величин может быть прямой и обратной.
Прямая пропорциональность
Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.
Рассмотрим пример прямой пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
При равномерном движении путь пропорционален времени движения. Если взять скорость v равной 5 км/ч, то пройденный путь s будет зависеть только от времени движения t:
| Скорость v = 5 км/ч | |||||
|---|---|---|---|---|---|
| Время t (ч) | 1 | 2 | 4 | 8 | 16 |
| Путь s (км) | 5 | 10 | 20 | 40 | 80 |
Из примера видно, что во сколько раз увеличивается время движения t, во столько же раз увеличивается пройденное расстояние s. В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.
В данном случае скорость (v = 5 км/ч) является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:
следовательно,
| 5 | = | 10 | = | 20 | = | 40 | = | 80 | = 5. |
| 1 | 2 | 4 | 8 | 16 |
Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:
| Время t = 2 ч | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 5 | 15 | 45 | 90 |
| Расстояние s (км) | 10 | 30 | 90 | 180 |
В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время (t = 2 ч):
следовательно,
| 10 | = | 30 | = | 90 | = | 180 | = 2. |
| 5 | 15 | 45 | 90 |
Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.
Формула прямой пропорциональности
Формула прямой пропорциональности:
y = kx,
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Обратная пропорциональность
Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.
Рассмотрим пример обратной пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь s равным 120 км, то потраченное на преодоление этого пути время t будет зависеть только от скорости движения v:
| Путь s = 120 км | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 10 | 20 | 40 | 80 |
| Время t (ч) | 12 | 6 | 3 | 1,5 |
Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.
В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:
s = vt,
следовательно,
10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.
Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Формула обратной пропорциональности
Формула обратной пропорциональности:
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
xy = k.
Математика
6 класс
Урок № 7
Прямая и обратная пропорциональность. Решение задач
Перечень рассматриваемых вопросов:
- Понятия прямой и обратной пропорциональной зависимости.
- Краткая запись условия задачи.
- Составление и решение пропорций по условию задачи.
- Решение задач на прямую и обратную пропорциональную зависимость.
Тезаурус
Равенство двух отношений называют пропорцией.
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Основная литература
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Прямая пропорциональность.
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Обратная пропорциональность.
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Для решения задач на пропорциональную зависимость, удобно составить таблицу или сделать краткую запись условия.
Столбцы таблицы соответствуют наименованиям зависимых величин.
Строки таблицы соответствуют значениям величин при первом и втором измерении.
Одинаково направленные стрелки показывают прямо пропорциональную зависимость, противоположно направленные – обратно пропорциональную.
Задача.
Поезд, скорость которого 55 км/ч, был в пути 5 часов. За сколько часов пройдёт этот же участок пути товарный поезд, скорость которого 45 км/ч?
Решение.
При постоянном пути скорость и время движения обратно пропорциональны.
Допустим, товарный поезд пройдёт этот же путь со скоростью 45 км/ч за x ч.
Сделаем краткую запись условия.
Задача.
Двигаясь с постоянной скоростью, велогонщик проезжает 40 метров за 3 с. Какой путь проедет велогонщик за 45 с?
Решение.
При постоянной скорости путь прямо пропорционален времени движения.
Пусть х м проедет велогонщик за 45 с.
Сделаем краткую запись условия.
Задача.
Усилие при восхождении на высоту 600 м равно усилию, требуемому для перехода 25 км по равнине. Турист поднялся в горы на 792 м. Какому расстоянию на равнине соответствует этот подъём?
Решение:
Решение.

Задача.
Четыре программиста могут написать игру за 12 месяцев. За сколько месяцев эту работу могут выполнить три программиста?
Решение.
Количество программистов и скорость написания игры – это обратно пропорциональная зависимость.
Разбор заданий тренировочного модуля
№ 1. Подстановка элементов в пропуски в тексте.
Подставьте нужные элементы в пропуски.
Пешеход шёл 3 часа со скоростью 8 км/ч. За сколько часов он пройдёт то же расстояние со скоростью 6 км/ч?
Решение:
При фиксированном расстоянии время в пути и скорость – ______ пропорциональны.
Пусть _____ часов – пешеход идёт со скоростью 6 км/ч.
Составим пропорцию:
_________
х=_______
х=_______(ч).
Правильный ответ.
Решение:
При фиксированном расстоянии время в пути и скорость – обратно пропорциональны.
Пусть х часов – пешеход идёт со скоростью 6 км/ч.
№ 2. Подстановка элементов в пропуски в таблице.
Заполните таблицу.
Поезд движется со скоростью 45 км/ч. Какое расстояние он пройдёт, если будет в пути 3 ч; 4 ч; 5 ч; 6 ч.
Варианты ответов:
135 км;
180 км;
225 км;
270 км.
Решение.
При постоянной скорости пройденный путь и время прямо пропорциональны. Скорость движения поезда 45 км/ч означает, что за 1 час поезд преодолевает расстояние в 45 км. Обозначим за x км – расстояние, которое поезд пройдёт за 3, 4, 5 и 6 часов.
Таким же способом находим расстояние, которое пройдёт поезд за 4, 5 и 6 часов, и подставляем соответствующие варианты в таблицу.
Ответ:
Понятие о прямой пропорциональности
Представьте, что вы задумали купить своих любимых конфет (или чего угодно, что вам очень нравится). У конфет в магазине своя цена. Предположим, 300 рублей за килограмм. Чем больше конфет вы купите, тем больше денег заплатите. То есть если захотите 2 килограмма – заплатите 600 р., а захотите 3 кило – отдадите 900 рублей. С этим вроде бы все ясно, верно?
Если да, то тогда вам сейчас ясно и что такоепрямая пропорциональность– это понятие, которое описывает отношение двух зависящих друг от друга величин. И отношение этих величин остается неизменным и постоянным: на сколько частей увеличивается или уменьшается одна из них, на столько же частей пропорционально увеличивается или уменьшается вторая.
Описать прямую пропорциональность можно такой вот формулой:f(x) = a*x, и a в этой формуле – постоянная величина (a = const). В нашем примере про конфеты цена – это постоянная величина, константа. Она не возрастает и не уменьшается, сколько бы конфет вы не задумали купить. Независимая переменная (аргумент)x– это то, сколько килограммов конфет купить вы собираетесь. А зависимая переменнаяf(x) (функция) – то, сколько денег вы в итоге заплатите за свою покупку. Так что можем подставить в формулу цифры и получить: 600 р. = 300 р. * 2 кг.
Промежуточный вывод такой: если возрастает аргумент, возрастает и функция, если аргумент убывает, функция тоже убывает
Функция и ее свойства
Функцией прямой пропорциональности является частный случай линейной функции. Если линейная функция это y = k*x + b, то для прямой пропорциональности это выглядит так: y = k*x, гдеk называется коэффициентом пропорциональности, и это всегда не равно нулю число. Вычислитьk легко – он находится как частное функции и аргумента: k = у/х.
Чтобы было нагляднее, возьмем еще один пример. Представьте, что из пункта А в пункт Б движется автомобиль. Его скорость – 60 км/ч. Если предположить, что скорость движения остается постоянной, то ее можно принять за константу. И тогда запишем условия в виде: S = 60*t, и эта формула аналогична функции прямой пропорциональности y = k*x. Проведем параллель дальше: если k = у/х, то и скорость автомобиля можно вычислить, зная расстояние между А и Б и затраченное на дорогу время: V = S/t.
А теперь от прикладного применения знаний о прямой пропорциональности вернемся обратно к ее функции. К свойствам которой относится:
-
областью ее определения является множество всех действительных чисел (а также его подмножества);
-
функция нечетная;
-
изменение переменных прямо пропорционально осуществляется по всей длине числовой прямой.
Прямая пропорциональность и ее график
График функции прямой пропорциональности – это прямая, которая пересекает точку начала координат. Чтобы его построить, достаточно отметить только еще одну точку. И соединить ее и начало координат прямой.
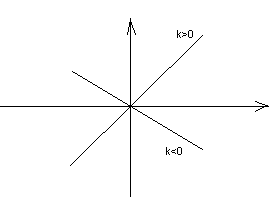
В случае с графикомk– это угловой коэффициент. Если угловой коэффициент меньше нуля (k < 0), то угол между графиком функции прямой пропорциональности и осью абсцисс тупой, а функция убывающая. Если угловой коэффициент больше нуля (k > 0), график и ось абсцисс образуют острый угол, а функция – возрастающая.
И еще одно свойство графика функции прямой пропорциональности напрямую связано с угловым коэффициентомk. Предположим, у нас две не идентичных функции и, соответственно, два графика. Так вот, если коэффициентыkэтих функций равны, их графики расположены на оси координат параллельно. А если коэффициентыkне равны друг другу, графики пересекаются.
Примеры задач
А теперь решим пару задач на прямую пропорциональность
Начнем с простого.
Задача 1: Представьте, что 5 куриц за 5 дней снесли 5 яиц. А если будет 20 куриц, сколько яиц они снесут за 20 дней?
Решение: Обозначим неизвестное какх. И рассуждать будем следующим образом: во сколько раз больше куриц стало? Разделим 20 на 5 и узнаем, что в 4 раза. А во сколько раз больше яиц снесут 20 куриц за те же 5 дней? Тоже в 4 раза больше. Значит, находим нашх так: 5*4*4 = 80 яиц снесут 20 куриц за 20 дней.
Теперь пример чуть сложнее, перефразируем задачу из «Всеобщей арифметики» Ньютона. Задача 2: Писатель за 8 дней может сочинить 14 страниц новой книги. Если бы у него были помощники, сколько бы человек понадобилось, чтобы написать 420 страниц за 12 дней?
Решение: Рассуждаем, что количество человек (писатель + помощники) увеличивается с увеличением объема работы, если бы ее пришлось сделать за то же количество времени. Но во сколько раз? Разделив 420 на 14, узнаем, что увеличивается в 30 раз. Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз, а таким образом: х = 1 (писатель) * 30 (раз) : 12/8 (дней). Преобразуем и выясним, что х = 20 человек напишут 420 страниц за 12 дней.
Решим еще задачу, похожую на те, что были у нас в примерах.
Задача 3: В одно и то же путешествие отправилось два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найдите скорость второго автомобиля.
Решение: Как вы помните, путь определяется через скорость и время – S = V *t. Поскольку путь оба автомобиля проделали одинаковый, мы можем приравнять два выражения: 70*2 = V*7. Откуда найдем, что скорость второго автомобиля, это V = 70*2/7 = 20 км/ч.
И еще пару примеров заданий с функциями прямой пропорциональности. Иногда в задачах требуется найти коэффициент k.
Задача 4: Даны функции у = — х/16 и у = 5х/2, определите их коэффициенты пропорциональности.
Решение: Как вы помните, k = у/х. Значит, для первой функции коэффициент равен -1/16, а для второй k = 5/2.
А еще вам может встретиться задание, как Задача 5: Запишите формулой прямую пропорциональность. Ее график и график функции у = -5х + 3 расположены параллельно.
Решение: Функция, которая дана нам в условии, – линейная. Нам известно, что прямая пропорциональность – частный случай линейной функции. А также мы знаем, что если коэффициенты k функций равны, их графики параллельны. Значит, все, что требуется – это вычислить коэффициент известной функции и задать прямую пропорциональность по знакомой нам формуле: y = k*x. Коэффициент k = -5, прямая пропорциональность: у = -5*х.
Вывод
Теперь вы узнали (или вспомнили, если уже проходили эту тему раньше), что называется прямой пропорциональностью, и рассмотрели ее примеры. Мы также поговорили о функции прямой пропорциональности и ее графике, решили несколько задач для примера.
Если эта статья оказалась полезной и помогла разобраться в теме, расскажите нам об этом в комментариях. Чтобы мы знали, смогли ли принести вам пользу.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Одно из основных понятий курса математики в 6 классе – это прямая и обратная пропорциональность. Если некоторая величина (время, масса, цена) изменяется, и одновременно другая величина (расстояние, объем, затраты) тоже меняется, то величины находятся в зависимости между собой, то есть пропорциональны друг другу.
Взаимосвязь между величинами не всегда означает наличие пропорциональности. Так, высота дерева растет с его возрастом, но не во столько же раз. Составление пропорций помогает решить многие задачи как в математике, так и на практике.
Прямая пропорциональность
Если при изменении одного параметра другой изменяется таким же образом, то эти величины прямо пропорциональны друг другу. В этой пропорции увеличение расстояния вдвое означает увеличение времени также двукратно.
Например, при движении автомобиля с постоянной скоростью, время, затраченное на преодоление расстояния, будет прямо пропорционально этому расстоянию. То есть, если 50 км автомобиль проедет за 1 час, то 100 км с той же скоростью он преодолеет за 2 часа.
Функция прямой пропорциональности и ее график
Эта зависимость описывается следующей формулой:
y = k * x.
Здесь k и называется коэффициентом пропорциональности.
Графически функция изображается прямой, которая пройдет через начальную точку координат. Строят график следующим образом: находят одну точку, затем чертят прямую через эту точку и начало координат.
Пример построения
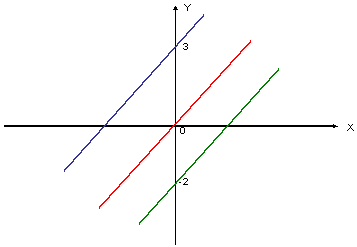
Нужно построить график у = 3х. Подставляем вместо х единицу, вычисляем y = 3, то есть находим координаты (1; 3). Отмечаем эту точку на координатной плоскости, проводим прямую линию через нее и точку (0; 0).
Вот так будет выглядеть график y = k * x при k > 0 (слева) и при k < 0 (справа).
Свойства функции прямой пропорциональности
Основные свойства следующие:
-
область определения, значений составляют все действительные числа;
-
является нечетной;
-
возрастает при всех значениях x, если k > 0;
-
если коэффициент со знаком «-», т. е. если k < 0, то убывает;
-
если k > 0, то прямая располагается в 1 — 3 координатных четвертях и образует острый угол с осью Х, если k < 0, то прямая находится во 2 — 4 четвертях и образует тупой угол с осью Х.
Обратная пропорциональность
Рост одного параметра ведет к уменьшению другого в такое же количество раз, и наоборот, при уменьшении одной величины другая увеличивается во столько же. Это значит, что они обратно пропорциональны друг другу.
Пример: трое рабочих выполнят порученную им работу за 2 часа, а 6 человек такое же задание осилят за 1 час. То есть двукратное увеличение числа работников привело к уменьшению затраченного времени вдвое. Конечно, если прочие факторы неизменны (производительность труда, условия работы).
Функция обратной пропорциональности и ее график
Функция задается формулой:
где k – любое действительное число, кроме 0.
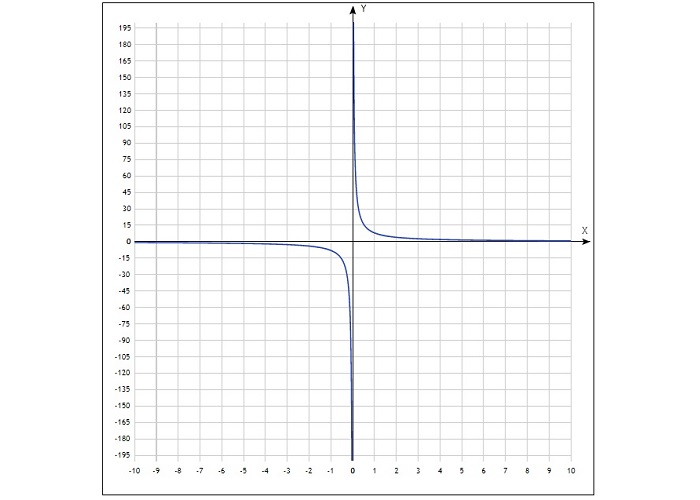
График данной зависимости — это гипербола, ее ветви находятся в 1 и 3 четвертях системы координат при k > 0, или во 2 и 4, если коэффициент меньше 0. Ветви гиперболы симметричны относительно точки (0; 0).
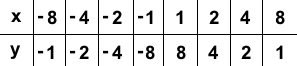
Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.
Пример построения
Нужно построить график функции y = 8/x.
Вот так выглядит таблица для данной функции:
Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:
Свойства функции обратной пропорциональности
Основные следующие:
-
области определения, значений функции D(y) – это все действительные числа, кроме 0, т. е. D(y):= x ≠ 0;
-
если коэффициент больше 0, функция является убывающей для всех x; если меньше 0, то y увеличивается для любых значений x;
-
оси координат 0х и 0у — это асимптоты по отношению к ветвям гиперболы, которые приближаются к ним, но не достигают их.
К составлению математических пропорций во многих случаях сводится решение самых разнообразных задач. Например, покупая 1 булочку по определенной цене, подсчитывают затраты на 4 булочки – получается в 4 раза больше.
Ускоряют шаг при ходьбе в 2 раза – достигнут цели вдвое быстрее. Вводят второго кассира в магазине – убывает очередь вдвое. Во всех этих случаях и им подобным применима теория о прямой и обратной пропорциональности.
Задача. Сторона квадрата равна (2) дм. Определи, как изменится периметр квадрата, если его сторону увеличить в (3) раза, в (4) раза, в (5) раз?
| Сторона квадрата, дм |
(2) |
(6) |
(8) |
(10) |
| Периметр квадрата, дм |
(8) |
(24) |
(32) |
(40) |
Заметим, что при увеличении стороны квадрата в (3) раза (была (2) дм, стала — (6) дм) периметр увеличился тоже в (3) раза (был (8) дм, стал — (24) дм).
Аналогично, при увеличении стороны квадрата в (4) раза (была (2) дм, стала — (8) дм) периметр увеличился тоже в (4) раза (был (8) дм, стал — (32) дм).
Вывод: при увеличении стороны квадрата в несколько раз периметр увеличивается во столько же раз.
Говорят, что сторона квадрата прямо пропорциональна его периметру.
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Обрати внимание!
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Проверим это утверждение на приведённой выше задаче.
Найдём в каждом случае отношение стороны квадрата к периметру:
Прямую пропорциональность можно задать формулой.
Формулу (y=kx), где (y) и (x) — переменные величины, а (k) — коэффициент, является постоянной величиной, называют формулой прямой пропорциональности.