|
Легко:
в месте пересечения последней линии и основания треугольника получаем идеальный прямой угол. система выбрала этот ответ лучшим Galina7v7 7 лет назад Я тоже не знаю.что такое-идеальная линейка.но есть идейка.Проведем прямую.на ней откладываем 2 равных отрезка.из центра отрезка произвольно проводим прямую.и на ней отложим такие же равные отрезки как и до этого .и каждую из точек соединим с концами 1-го отрезка.получили прямоугольник т.к. диагонали равны.и в точке пересечения делятся пополам. и угла полученные = 90 град-в. …Вижу «оригинальность «понятия идеальной линейки-ею мерять нельзя..а что ею можно делать?мух бить?Или тупо приложить к бумаге и провести прямой угол по контуру-она же «идеальная линейка»и угол ее прямой и идеальный» bezdelnik 7 лет назад Построить теоретически точно прямой угол с помощью идеальной линейки без делений можно так. На листе бумаги по линейке проводим произвольную прямую, затем складываем лист на две части так, чтобы части прямой совпали. Тогда в пересечении прочерченной прямой с линией складки получим 4-ре прямых угла. Знаете ответ? |
Download Article
Download Article
Often times, you are required to construct some angles without using a protractor. This article teaches you how to draw a 90 degrees angle using a compass and a ruler.
-
1
Mark the vertex of your angle anywhere on the paper. Let us name this point as M.
-
2
Draw a ray MN, extending in any direction and of any length. This will be one of the arms of our angle.[1]
Advertisement
-
3
Place tip of the compass on point M and draw a circle cutting the ray MN at some point (say P).[2]
-
4
Keep the width of the compass the same. Then place its tip on P and draw an arc cutting the circle at some point (say Q).
-
5
Keep the width of the compass the same. Place its tip on Q and draw another arc cutting the circle at another point (say R).[3]
-
6
Keep the tip of the compass still on Q. Draw another arc somewhere outside the circle. For carrying out this step, you can set the width of the compass to any measure.[4]
-
7
Keep the same width of the compass (as set in the previous step). Now place its tip on R and draw another arc which cuts the arc drawn in the previous step at some point (say S).
-
8
Connect the points M and S with a straight line. Extend it to form a ray ML.[5]
- The measure of the angle LMN is 90O.
Advertisement
-
1
Draw a straight line. On a piece of paper, draw a line segment of any convenient length. Make it horizontal for the sake of simplicity, but it could be at any angle. Label the line segment AB.[6]
-
2
Pick any point on AB. Mark it, and label it O. O can be anywhere on the line segment, including at either end point (A or B). For convenience, let’s put O somewhere near the middle of AB. The line segment could now be referred to as AOB.
-
3
Grab a compass. Open the compass to a radius a little shorter than either AO or OB. Now place the compass point at O. Strike short arcs through AB on either side of O. The two arcs should have the same radius. Label those two points of intersection C and D. Now the line segment could be referred to as ACODB.[7]
-
4
Strike two more arcs. Place the compass point at C, and strike an arc to one side of the line segment. Then place the compass point at D, and strike a second arc of the same radius and on the same side of the line segment. Make sure those two arcs intersect. Call that point of intersection E.[8]
-
5
Draw the 90° angle. Draw a straight line from E to O. Line segment EO forms a 90° angle with line segment AB. It actually forms two 90° angles at O. If you were to extend EO beyond AB, you would form four 90° angles at O.[9]
- Note that you can draw a 90° angle at either end of line segment AB if you want to (in other words at point A or point B). Simply extend AB beyond A or beyond B, and then follow the above steps. Point A (or point B) would serve as point O in the above instructions.
- This is essentially the same method featured in How to Construct a Perpendicular Line to a Given Line Through Point on the Line, Method 2.
Advertisement
Add New Question
-
Question
How do I draw a right angle triangle?
First construct a 90° angle as shown above. Extend each leg of the angle any convenient length. Draw a line from the end of one leg to the end of the other. You have a right triangle.
-
Question
How do I construct a 15 degree angle?
First, make a 60 degree angle by constructing an equilateral triangle. Use angle bisection construction to make a 30 degree angle. Bisect the 30 degree angle again to make a 15 degree angle.
-
Question
Can I draw a 133-degree angle?
There is no way to construct such an angle using a compass and a ruler. That’s why they invented the protractor.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
Things You’ll Need
- Paper
- Pen or pencil
- Ruler or another straightedge
- Compass
References
About This Article
Thanks to all authors for creating a page that has been read 112,974 times.
Reader Success Stories
-
Payal Sharma
Sep 27, 2016
«A really detailed and elaborate answer! Keep it going! Better than my maths teacher!»
Did this article help you?
Загрузить PDF
Загрузить PDF
Одна из проблем при построении угла или треугольника – сделать угол прямым. Конечно, угол не обязательно должен быть идеально прямым, но при проектировании нужно постараться сделать так, чтобы максимально приблизить угол к значению 90 градусов. Если не получится, есть вероятность, что ковровое покрытие будет положено неровно относительно какой-либо стены. Метод 3-4-5 полезен для небольших строительных проектов, чтобы все покрытия были ровными и совпадали друг с другом, как и планировалось.
-
1
Поймите, в чем суть правила 3-4-5. Если у треугольника есть три стороны со значениями 3, 4 и 5 см (или кратное им значение), это прямоугольный треугольник, угол между сторонами с меньшими значениями составляет 90 градусов. Если у вас получилось построить треугольник, исходя из значений угла, то можно точно сказать, что угол прямоугольный. Это правило основано на теореме Пифагора: A2 + B2 = C2 (в прямоугольном треугольнике). Где С – самая длинная сторона (гипотенуза), А и В –остальные стороны (катеты).[1]
- Правило 3-4-5 очень удобно проверить благодаря целым числам. Итак, опираясь на математические расчеты: 32 + 42 = 9 + 16 = 25 = 52.
-
2
Отмерьте от угла 3 см (или 3 м) на одной стороне. Можно взять любую меру длины. Пометьте отмеренный участок точкой.
- Можно умножить каждое число на одно и то же число – и это правило все равно сработает. Например, это правило будет работать для треугольника со сторонами 30-40-50 сантиметров или метров. Если у вас большая комната, можно использовать следующие числа: 9-12-15, 6-8-10 метров.
-
3
Отмерьте четыре метра (или длину со значением, которое кратно четырем) на другой стороне. То же самое, если у вас получится сделать треугольник, то угол между этими двумя сторонами будет равен 90 градусам. Снова пометьте отмеренный участок точкой.
-
4
Теперь измерьте расстояние между этими двумя метками. Если расстояние кратно пяти, то можно точно сказать, что угол составляет 90 градусов.[2]
- Если расстояние меньше, чем 5 единиц (метров), значит, угол острый (меньше 90 градусов). Если есть такая возможность, нужно немного раздвинуть стороны, образующие этот угол.
- Если расстояние между метками составляет больше 5 единиц (метров), значит, угол тупой (то есть больше 90 градусов). Если есть такая возможность, нужно свести стороны, образующие угол, поближе друг к другу, чтобы угол получился прямым. Строя прямой угол, можно использовать прямой угол рамки.
- Получив прямой угол в 90 градусов, можно проверить остальные углы комнаты, чтобы убедиться в том, что они прямые.
Реклама
Советы
- Этот метод считается более точным, чем с использованием специального инструмента угольника, потому что этот инструмент может быть слишком мал для измерения на больших расстояниях и площадях.
- Чем большую меру измерения вы возьмете, тем точнее будет результат.[3]
Реклама
Что вам понадобится
- Рулетка
- Карандаш
Об этой статье
Эту страницу просматривали 96 028 раз.
Была ли эта статья полезной?
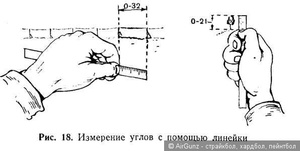
Математика. Это страшное для многих слово, которое пугало достаточное количество школьников в своё время. Цифры, формулы и расчёты поддавались только самым пытливым. И с каждым годом этот сложный предмет становился всё сложнее и сложнее.
- Действительно ли прямой угол?
- Что понадобится для определения прямого угла?
- Как можно вычислить прямой угол?
- Вывод
В старших классах появляется геометрия и всё становится ещё сложнее и непонятнее. Возможно, многие хоть раз в жизни, но в сердцах проклинали непонятную им науку и задавались вопросом, зачем это вообще нужно, и понадобится ли это в жизни.
Возможно, в повседневной жизни применить полученные в школе знания не удавалось. Вряд ли требовалось посреди белого дня высчитывать логарифмы и квадратные уравнения или доказывать, что две параллельные никогда не сойдутся. Но, где уж точно могут понадобиться знания геометрии и математике, так это в строительстве и при осуществлении ремонта.
В данной статье речь пойдёт о вычислении прямого угла, что требуется при строительстве зданий. Точность при возведении строений должна быть соблюдена в обязательном порядке, ведь только точные расчёты могут избавить от перекосов и нестабильности организации всего здания. Вычисление прямого угла при строительстве — не такой уж и трудный процесс, при котором потребуется знание и применение некоторых простых правил математики и геометрии. Подробнее об этом будет рассказано ниже.
Действительно ли прямой угол?
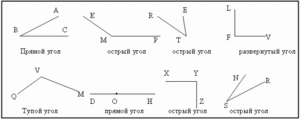
И, в принципе, они правы. Получить его весьма сложно, особенно если наблюдается неровность фундамента, на котором осуществляется строительство здания. Но, даже учитывая это обстоятельство, ни в коем случае нельзя делать вывод, что расчёт прямого угла можно делать просто «на глаз». В любом случае, если не представляется возможным вычислить идеальный прямой угол, то требуется достичь наиболее приближённого значения к идеальному углу в 90 градусов. И этого можно добиться, используя незатейливые инструменты и не самые сложные математические знания и познания в геометрии.
Что понадобится для определения прямого угла?

Для вычисления прямого угла нужно взять:
- Карандаш;
- Строительную рулетку.
И всё. Вот так вот всё просто.
Как можно вычислить прямой угол?
Итак, в этой статье будет описан принцип 3-4-5 при определении угла в 90 градусов. Ничего сложного в этом нет. Потребуется просто лишь чуть пораскинуть мозгами и вникнуть во все расчёты, которые смогут помочь в проверке угла.
Итак, нужно обозначить следующие шаги:
Для начала стоит разобраться в том, почему принцип так обозначен — 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
- Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра — предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
- В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
- После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
- Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
- Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
- В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
- Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.
Вывод
Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство, которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.
При использовании предложенных величин, ключевым становится финальный замер между двумя отметками, которые были сделаны ранее. Расстояние, которое будет равняться точно 5 метрам, покажется, что он прямой. Если же величина будет больше или меньше 5 метров, это будет означать, что он прямым не является.









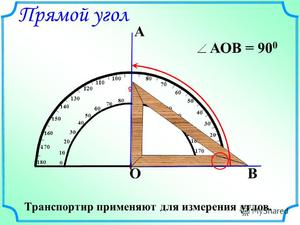 Для начала стоит разобраться в том, почему принцип так обозначен — 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
Для начала стоит разобраться в том, почему принцип так обозначен — 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;