From Wikipedia, the free encyclopedia
A right angle is equal to 90 degrees.
A line segment (AB) drawn so that it forms right angles with a line (CD).
In geometry and trigonometry, a right angle is an angle of exactly 90 degrees or 
/2 radians[1] corresponding to a quarter turn.[2] If a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles.[3] The term is a calque of Latin angulus rectus; here rectus means «upright», referring to the vertical perpendicular to a horizontal base line.
Closely related and important geometrical concepts are perpendicular lines, meaning lines that form right angles at their point of intersection, and orthogonality, which is the property of forming right angles, usually applied to vectors. The presence of a right angle in a triangle is the defining factor for right triangles,[4] making the right angle basic to trigonometry.
Etymology[edit]
The meaning of right in right angle possibly refers to the Latin adjective rectus ‘erect, straight, upright, perpendicular’. A Greek equivalent is orthos ‘straight; perpendicular’ (see orthogonality).
In elementary geometry[edit]
A rectangle is a quadrilateral with four right angles. A square has four right angles, in addition to equal-length sides.
The Pythagorean theorem states how to determine when a triangle is a right triangle.
Symbols[edit]
Right triangle, with the right angle shown via a small square.
Another option of diagrammatically indicating a right angle, using an angle curve and a small dot.
In Unicode, the symbol for a right angle is U+221F ∟ RIGHT ANGLE (∟). It should not be confused with the similarly shaped symbol U+231E ⌞ BOTTOM LEFT CORNER (⌞, ⌞). Related symbols are U+22BE ⊾ RIGHT ANGLE WITH ARC (⊾), U+299C ⦜ RIGHT ANGLE VARIANT WITH SQUARE (⦜), and U+299D ⦝ MEASURED RIGHT ANGLE WITH DOT (⦝).[5]
In diagrams, the fact that an angle is a right angle is usually expressed by adding a small right angle that forms a square with the angle in the diagram, as seen in the diagram of a right triangle (in British English, a right-angled triangle) to the right. The symbol for a measured angle, an arc, with a dot, is used in some European countries, including German-speaking countries and Poland, as an alternative symbol for a right angle.[6]
Euclid[edit]
Right angles are fundamental in Euclid’s Elements. They are defined in Book 1, definition 10, which also defines perpendicular lines. Definition 10 does not use numerical degree measurements but rather touches at the very heart of what a right angle is, namely two straight lines intersecting to form two equal and adjacent angles.[7] The straight lines which form right angles are called perpendicular.[8] Euclid uses right angles in definitions 11 and 12 to define acute angles (those smaller than a right angle) and obtuse angles (those greater than a right angle).[9] Two angles are called complementary if their sum is a right angle.[10]
Book 1 Postulate 4 states that all right angles are equal, which allows Euclid to use a right angle as a unit to measure other angles with. Euclid’s commentator Proclus gave a proof of this postulate using the previous postulates, but it may be argued that this proof makes use of some hidden assumptions. Saccheri gave a proof as well but using a more explicit assumption. In Hilbert’s axiomatization of geometry this statement is given as a theorem, but only after much groundwork. One may argue that, even if postulate 4 can be proven from the preceding ones, in the order that Euclid presents his material it is necessary to include it since without it postulate 5, which uses the right angle as a unit of measure, makes no sense.[11]
Conversion to other units[edit]
A right angle may be expressed in different units:
- 1/4 turn
- 90° (degrees)
- π/2 radians
- 100 grad (also called grade, gradian, or gon)
- 8 points (of a 32-point compass rose)
- 6 hours (astronomical hour angle)
Rule of 3-4-5[edit]
Throughout history, carpenters and masons have known a quick way to confirm if an angle is a true «right angle». It is based on the most widely known Pythagorean triple (3, 4, 5) and so called the «rule of 3-4-5». From the angle in question, running a straight line along one side exactly 3 units in length, and along the second side exactly 4 units in length, will create a hypotenuse (the longer line opposite the right angle that connects the two measured endpoints) of exactly 5 units in length. This measurement can be made quickly and without technical instruments. The geometric law behind the measurement is the Pythagorean theorem («The square of the hypotenuse of a right triangle is equal to the sum of the squares of the two adjacent sides»).
Thales’ theorem[edit]
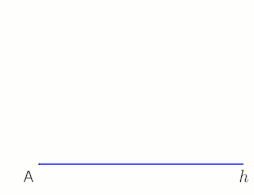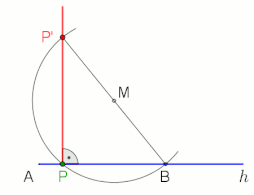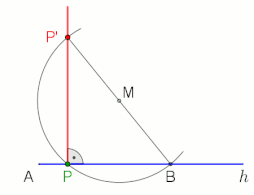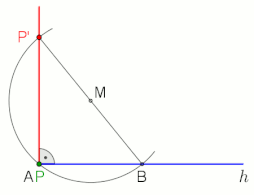
Construction of the perpendicular to the half-line h from the point P (applicable not only at the end point A, M is freely selectable), animation at the end with pause 10 s
Alternative construction if P outside of the half-line h and the distance A to P’ is small (B is freely selectable),
animation at the end with pause 10 s
Thales’ theorem states that an angle inscribed in a semicircle (with a vertex on the semicircle and its defining rays going through the endpoints of the semicircle) is a right angle.
Two application examples in which the right angle and the Thales’ theorem are included (see animations).
See also[edit]
- Cartesian coordinate system
- Types of angles
References[edit]
- ^ «Right Angle». Math Open Reference. Retrieved 26 April 2017.
- ^ Wentworth p. 11
- ^ Wentworth p. 8
- ^ Wentworth p. 40
- ^ Unicode 5.2 Character Code Charts Mathematical Operators, Miscellaneous Mathematical Symbols-B
- ^ Müller-Philipp, Susanne; Gorski, Hans-Joachim (2011). Leitfaden Geometrie [Handbook Geometry] (in German). Springer. ISBN 9783834886163.
- ^ Heath p. 181
- ^ Heath p. 181
- ^ Heath p. 181
- ^ Wentworth p. 9
- ^ Heath pp. 200–201 for the paragraph
- Wentworth, G.A. (1895). A Text-Book of Geometry. Ginn & Co.
- Euclid, commentary and trans. by T. L. Heath Elements Vol. 1 (1908 Cambridge) Google Books
В данной публикации мы рассмотрим, что такое прямой угол, перечислим основные геометрические фигуры, в которых он встречается, а также разберем пример задачи по этой теме.
- Определение прямого угла
- Фигуры с прямыми углами
- Пример задачи
Определение прямого угла
Угол является прямым, если его градусная мера равняется 90 градусам.
На чертежах для обозначения такого угла используется не круглая дуга, а квадратная.
Прямой угол составляет половину развернутого угла (180°) и в радианах равняется π/2.
Фигуры с прямыми углами
1. Квадрат – ромб, все углы которого равны 90°.
2. Прямоугольник – параллелограмм, все углы которого, также, являются прямыми.
3. Прямоугольный треугольник – один из его углов прямой.
4. Прямоугольная трапеция – хотя бы один из углов равняется 90°.
Пример задачи
Известно, что в треугольнике один из углов является прямым, а два остальных равны между собой. Найдем неизвестные значения.
Решение
Как мы знаем из теоремы о сумме углов треугольника, она равняется 180°.
Следовательно, на два неизвестных угла приходится 90° (180° – 90°). Значит каждый из них равняется 45° (90° : 2).
Как найти прямой угол
Существует несколько геометрических определений прямого угла:
— прямой угол – это смежный угол или угол, который равен смежному углу;
— прямым углом является угол, который равен 90 градусов;
— для вычисления прямого угла необходимы измерения углов- a и b;
— угол равный 90 градусов, составляющий четверть целого угла и половину развернутого называется прямым углом.
Инструкция
Данные понятия и определения указывают на то, что все без исключения прямые углы равны и любые два угла могут быть сравнимы. А само сравнение двух углов с прямым углом вводит понятие — острого и тупого угла.
Для того, чтобы найти прямой угол, необходимо вводить измерение градуса угла с помощью транспортира, если он равен 90 градусов, то, следовательно, этот угол является прямым.
Ряд геометрических фигур имеет один или несколько прямых углов. К таким фигурам относятся прямоугольный треугольник (имеет одни прямой угол), параллелограмм (все углы его прямые), квадрат является ромбом, у которого все углы прямые, а также прямоугольная трапеция с одним прямым углом.
Построить прямой угол самостоятельно без геометрических инструментов можно с использованием отвеса (любая нитка с грузом), уровень для горизонтальной и стеклянная деталь для вертикальной поверхности.
Видео по теме
Источники:
- как вычислить прямой угол
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Понятие угла является одним из наиболее важных определений в геометрии. У́гол — геометрическая фигура, образованная двумя лучами, сторонами угла, выходящими из одной точки, которая называется вершиной угла.
Понятия равенства и суммы углов часто используется в тригонометрии. Например, углы (15,30,45) градусов.
Градусы углов
градусная мера угла и наиболее распространенными единицами измерения угла являются градус и радиан. Один градус — это (frac{1}{360}) полного круга. (90) градусов — это четверть круга, (180) – половина круга (это то, сколько градусов развернутый угол), (270) — три четверти круга (это то, сколько градусов тупой угол) и (360) это целый круг.
Сколько градусов составляет прямой угол?
Прямой угол равен (90) градусов, острый угол больше (0) и меньше (90) градусов и тупой угол больше (90) градусов и меньше (180) градусов. Развернутый угол равен (180) градусам.
Мы изучаем углы от (0)° до (360)°, но есть углы больше (360)° и отрицательные углы.
Градусы могут быть разделены на минуты и секунды. Каждый градус делится на (60) равных частей, которые называются минутами. Так семь с половиной градусов можно сказать (7) градусов и (30) минут и записать (7) ° (30)‘. Каждая минута делится на (60) равных частей, каждая из которых равна одной секунде. Например, (2) градуса (5) минут (30) секунд записывается (2)° (5)‘ (30)«. Деление градуса на минуты и секунды аналогично делению часа на минуты и секунды времени.
Виды углов
-
Острые углы: углы, чья мера меньше 90 градусов.
-
Прямые углы: углы, чья мера равна 90 градусов.
-
Тупые углы: углы, чья мера больше 90 градусов.
-
Равные углы: углы, чьи меры совпадают.
-
Смежные углы: два угла, которые имеют общую вершину и общую сторону, но не пересекаются внутри этой стороны.
-
Вертикальные углы: два угла, чьи стороны являются противоположными лучами пересекающихся прямых. Вертикальные углы равны между собой.
-
Смежно-вертикальные углы: два угла, один из которых является вертикальным углом, а другой — смежным с ним углом. Смежно-вертикальные углы равны между собой.
Часто задаваемые вопросы:
✅ Что такое угол в математике?
↪ Угол — это геометрическая фигура, которая образуется двумя лучами, исходящими из общей начальной точки. Начальная точка угла называется вершиной, а лучи — сторонами угла. Измеряется в градусах или радианах.
✅ Какие бывают углы?
↪ Углы бывают острые (меньше 90 градусов), прямые (равен 90 градусов), тупые (больше 90 градусов), равные (углы совпадают), смежные (имеют общую вершину и общую сторону, но не пересекаются внутри этой стороны), вертикальные (стороны являются противоположными лучами пересекающихся прямых), смежно-вертикальные (два угла, один из которых является вертикальным углом, а другой — смежным с ним углом).
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!