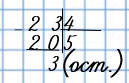Математика. 3 класс
Урок № 49. Проверка деления с остатком
Перечень вопросов, рассматриваемых в теме:
1. Как разделить двузначное число на двузначное с остатком?
2. Как выполнить проверку деления с остатком?
3. Какие приёмы проверки частного и остатка удобные?
Глоссарий по теме:
Деление – это обратное действие умножению.
Делимое – компонент деления, число которое делят.
Делитель – компонент деления, число на которое делят.
Частное – результат деления.
Неполное частное – результат деления с остатком.
Обязательная литература и дополнительная литература:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для
общеобразовательных организаций М.; Просвещение, 2017. – с. 32.
2. Математика. 3 класс. Часть 2. / Л. Г. Петерсон. – М.: Ювента, 2013 – с. 96.
Теоретический материал для самостоятельного изучения
Ребята, вы уже знакомы со случаями деления с остатком. Теперь нам нужно научиться выполнять проверку деления двузначного на двузначное с остатком.
Рассмотрим пример.
Восемьдесят пять разделить на пятнадцать — получим частное пять и остаток десять.
85 : 15 = 5 (ост. 10)
Выполним проверку.
Первое в чём должны убедиться, это в том, что остаток меньше делителя.
Десять меньше пятнадцати.
10 < 15
Далее делитель умножаем на частное:
пятнадцать умножаем на пять получается семьдесят пять и прибавляем остаток десять. Получаем делимое — восемьдесят пять.
15 ∙ 5 + 10 = 85
В случае деления, когда делимое меньше делителя, действуем так же.
Девятнадцать разделить на двадцать равно нулю и остаток девятнадцать. Девятнадцать меньше двадцати.
Двадцать умножаем на нуль и прибавляем девятнадцать равно девятнадцати.
19 : 20 = 0 (ост. 19)
Проверка: 1) 19 < 20,
2) 20 ∙ 0 + 19 = 19
Выполним тренировочные задания.
№1. Как проверить деление 34 : 16 = 2 (ост. 2)?
1) 2 ∙ 16 + 2 = 34;
2) 2 ∙ 16 = 34;
Ответ: 2 ∙ 16 + 2 = 34.
№ 2. Вставьте пропущенные числа:
49 : 15 = ____ (ост. ___)
15 ∙ ___ + ____ = 49
Ответ: 49 : 15 = 3 (ост. 4)
15 ∙ 3 + 4 = 49
№ 3. Соотнесите условие задачи, решение и проверку:
«40 банок с вареньем упаковывали в ящики по 6 штук. Сколько ящиков потребовалось? Сколько банок осталось?»
40 : 6 = 6 (ост. 3) — 6 ∙ 6 + 3 = 40
40 : 6 = 5 (ост. 10) — 6 ∙ 5 + 10 = 40
40 : 6 = 6 (ост. 4) — 6 ∙ 6 + 4 = 40
Ответ: 40 : 6 = 6 (ост. 4) — 6 ∙ 6 + 4 = 40
№ 4. Решите примеры и укажите, какой остаток получится при делении:
57 : 42;
28 : 17;
89 : 22;
5 : 11.
Правильный вариант:
|
Остаток больше 10 |
|
57 : 42 28 : 17 |
|
Остаток меньше 10 |
|
89 : 22 5 : 11 |
№ 5. Расшифруйте слово. Что оно означает в математике?
Ответ:
Деление с остатком.
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.
16=5⋅3+1
a=b⋅c+d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6<7.
Подставим в формулу и проверим правильно ли мы решили пример:
7⋅36+6=252+6=258
б) Делим столбиком:
1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1<8.
Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873
Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.
Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.
Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)
Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22
б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107
Задача:
Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?
Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400
Ответ: 30 кусков получиться и 10 см. проволоки останется.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Деление
- Деление с остатком
Начнём рассмотрение новой темы с решения задачи.
Мама принесла 8 конфет и разделила их поровну между двумя детьми. Сколько конфет получил каждый?
8 : 2 = 4 (к.)
Каждый ребёнок получил по 4 конфеты.
На следующий день мама опять принесла 8 конфет, но в гостях у её детей была ещё одна подружка. Мама опять разделила конфеты поровну, но уже между тремя детьми. Сколько конфет получил каждый ребёнок?
Каждый получил по 2 конфеты и 2 конфеты остались лишними.
Как это записать?
8 : 3 = 2 (ост. 2)
Как сделать проверку?
2 • 3 + 2 = 8
Правило 1
Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.
16 : 7 = 2 (ост. 2)
23 : 8 = 2 (ост. 7)
Правило 2
При делении с остатком остаток всегда должен быть меньше делителя.
43 : 8 = 5 (ост. 3)
остаток 3 < делимого 5
34 : 4 = 8 (ост. 2)
остаток 2 < делимого 4
Правило 3
Если делимое меньше делителя, в частном получается ноль, а остаток равен делимому.
7 : 10 = 0 (ост. 7)
6 : 9 = 0 (ост. 6)
Порядок решения
14 : 5 = 2 (ост. 4)
1. Нахожу наибольшее число до 14, которое делится на 5 без остатка. Это число 10.
10 : 5 = 2
2. Вычитаю из делимого найденное число: 14 − 10 = 4
3. Сравниваю остаток с делителем
4 < 5
Решение верно.
Проверка деления с остатком
1. Умножаю неполное частное на делитель.
2. Прибавляю остаток к полученному результату.
3. Сравниваю полученный результат с делимым, он должен быть МЕНЬШЕ.
Деление в столбик
В 23 содержится 5 раз по 4, и ещё остаётся 3.
Решение записывают так:
23 : 4 = 5 (ост. 3) или так:
, где 23 — делимое, 4 — делитель, 5 — неполное частное, а 3 — остаток.
Советуем посмотреть:
Табличное деление
Внетабличное деление
Деление суммы на число
Деление на однозначное число
Деление чисел, оканчивающихся нулями
Свойства деления
Деление
Правило встречается в следующих упражнениях:
2 класс
Страница 76. Урок 29,
Петерсон, Учебник, часть 3
Страница 77. Урок 29,
Петерсон, Учебник, часть 3
Страница 79. Урок 30,
Петерсон, Учебник, часть 3
Страница 80. Урок 30,
Петерсон, Учебник, часть 3
Страница 81. Урок 31,
Петерсон, Учебник, часть 3
Страница 82. Урок 31,
Петерсон, Учебник, часть 3
Страница 84. Урок 32,
Петерсон, Учебник, часть 3
Страница 87. Урок 33,
Петерсон, Учебник, часть 3
Страница 108. Повторение,
Петерсон, Учебник, часть 3
3 класс
Страница 58. Тест 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 85. ПР 3. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 4,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 39. Урок 14,
Петерсон, Учебник, часть 1
Страница 71. Урок 24,
Петерсон, Учебник, часть 1
Страница 87. Урок 32,
Петерсон, Учебник, часть 1
Страница 109. Урок 42,
Петерсон, Учебник, часть 1
Страница 31. Урок 13,
Петерсон, Учебник, часть 2
Страница 91. Урок 40,
Петерсон, Учебник, часть 2
4 класс
Страница 20,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 18,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 39,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 63. ПР 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 28,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 31,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Задание 533,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 954,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1083,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1724,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1793,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1827,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 552,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 8,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Номер 141,
Мерзляк, Полонский, Якир, Учебник
Номер 860,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 351,
Мерзляк, Полонский, Якир, Учебник
Номер 352,
Мерзляк, Полонский, Якир, Учебник
Номер 672,
Мерзляк, Полонский, Якир, Учебник
Номер 1147,
Мерзляк, Полонский, Якир, Учебник
Задание 486,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 602,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1027,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1158,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1159,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 8,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 422,
Мерзляк, Полонский, Якир, Учебник
Номер 574,
Мерзляк, Полонский, Якир, Учебник
Номер 580,
Мерзляк, Полонский, Якир, Учебник
Номер 607,
Мерзляк, Полонский, Якир, Учебник
Номер 773,
Мерзляк, Полонский, Якир, Учебник
Номер 784,
Мерзляк, Полонский, Якир, Учебник
Номер 856,
Мерзляк, Полонский, Якир, Учебник
Номер 1031,
Мерзляк, Полонский, Якир, Учебник
Номер 1045,
Мерзляк, Полонский, Якир, Учебник
Номер 1156,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 47,
Мерзляк, Полонский, Якир, Учебник
Номер 139,
Мерзляк, Полонский, Якир, Учебник
Номер 141,
Мерзляк, Полонский, Якир, Учебник
Номер 207,
Мерзляк, Полонский, Якир, Учебник
Номер 212,
Мерзляк, Полонский, Якир, Учебник
Номер 241,
Мерзляк, Полонский, Якир, Учебник
Номер 305,
Мерзляк, Полонский, Якир, Учебник
Номер 306,
Мерзляк, Полонский, Якир, Учебник
Номер 307,
Мерзляк, Полонский, Якир, Учебник
В Ы У Ч И! З А П О М Н И!
Н А У Ч И С Ь В Ы П О Л Н Я Т Ь!
Алгоритм выполнения деления с остатком и его проверка.
- Определи в числовом выражении компоненты деления (делимое, делитель).
- В делимом определи, какое самое большое число можно разделить без остатка на делитель.
- Выполни деление. Раздели самое большое полученное число на делитель. Результат деления запиши в частном.
- Вычисли остаток. Для этого из делимого вычти то, число которое, разделили без остатка на делитель. Запиши, чему равен остаток.
Помни: Остаток всегда должен быть меньше делителя.
Выполнение проверки деления с остатком.
Выучи правило и научись его применять:
Чтобы выполнить проверку деления с остатком, нужно частное умножить на делитель и прибавить остаток.
- Выполни проверку письменно или устно, применяя правило. Сделай вывод: если, при проверке получилось делимое, то деление выполнено правильно.
Н А П Р И М Е Р:
Выполним деление: 39 : 5
- Определяем в выражении компоненты деления:
39 – это делимое, 5 – это делитель.
- Определяем, какое самое большое число до 39 делится на 5 без остатка ( Для этого вспомним таблицу умножения и деления). До 39 делится без остатка на 5 –число 35.
- Делим 35 на 5 – получается 7. В частном запишем 7.
- Вычислим остаток. Для этого из делимого 39 вычтем то число, которое делили без остатка на делитель – это число 35.
39 – 35 = 4 (4 – это остаток).
- Выполняем проверку. Применяем правило.
Частное – 7 умножим на делитель 5 и прибавим остаток 4, получается – 39 – это делимое. Значит деление с остатком выполнено верно.
Образец записи в тетради:
Проверка:
39: 5 = 7 (ост. 4) 7 ∙ 5 + 4 = 39
Тема
«Деление с остатком. Проверка деления с остатком»,
3
класс, УМК «Перспектива» — объяснение материала
Учитель
начальных классов МБОУ СШ № 7 г. Павлово Нижегородской обл. Зуева Елена
Витальевна
ДЕЛЕНИЕ
С ОСТАТКОМ
Вначале
вспомним, как называются компоненты деления
Не все числа можно
разделить с помощью таблицы умножения. В таком случае выполняется деление с
остатком.
►
Чтобы выполнить деление с остатком, нужно вспомнить, какое число в таблице
умножения ближе всех к делимому, но меньше его.
1) Например: 28 :
3 – вспоминаю таблицу на 3. Самое близкое число к 28 – это 27. Значит, буду
делить 27 на 3, получается 9 – это частное.
Теперь находим
остаток. Для этого от 28 отнимаю 27, получается 1 – это и есть остаток.
Записывают так
28 : 3 = 9 (ост. 1)
2) Примеры
рассуждения:
|
14 : 3 = ? 12 : 3 = 4 14 – 12 = 2 14 : 3 = 4 (ост. 2) |
52 : 6 = ? 48 : 6 = 8 52 – 48 = 4 52 : 6 = 8 (ост. 4) |
37 : 8 = ? 32 : 8 = 4 37 – 32 = 5 37 : 8 = 4 (ост. 5) |
►
Остаток всегда должен быть меньше делителя! Иначе
этот остаток можно будет ещё раз разделить на делитель.
16 : 5 = 2 (ост.
6) – неверно, так как 6 > 5 и его ещё раз можно разделить на 5.
16 : 5 = 3 (ост.
1) – верно, так как 1 < 5
► Бывает, что делимое
меньше делителя. Например: 3 ручки раздали 5 детям. Сколько ручек получит
каждый ребёнок? (ни одной, то есть — 0). Если делимое меньше делителя, частное
будет – 0, делимое будет остатком.
3 : 5 = 0 (ост. 3)
7 : 9 = 0 (ост. 7)
► Для того, чтобы
изучить и отработать тему «Деление с остатком», выполни задания на платформе
Учи.ру для 3 класса
1 – математика
2 – раздел
«Умножение и деление»
3 – тема
«Внетабличное умножение и деление»
4 – «Деление с
остатком», 3 карточки
ПРОВЕРКА
ДЕЛЕНИЯ С ОСТАТКОМ
►
Как выполнить проверку деления с остатком?
Для этого частное
нужно умножить на делитель (или наоборот) и к результату прибавить остаток. В
итоге должно получиться делимое.
Например:
45 : 7 = 6 (ост.
3)
Проверка:
6 ٠ 7 + 3 = 45
или 7 ٠ 6 + 3 = 45
►
Найдём верно и неверно решённые выражения
1) 21 : 4 = 5
(ост. 1) – верно, так как 4 ٠
5 + 1 = 21 и остаток 1 < делителя 4
2) 27 : 5 = 4
(ост. 7) – неверно. Даже если выполнив проверку 4 ٠
5 + 7 = 27 вы получаете заданное делимое, выражение решено неверно, так как
остаток 7 > делителя 5.
► Для того, чтобы
изучить и отработать тему «Проверка деления с остатком», выполни задания на
платформе Учи.ру для 3 класса
1 – математика
2 – раздел
«Умножение и деление»
3 – тема
«Внетабличное умножение и деление»
4 – «Проверка
деления с остатком», 3 карточки
► Для закрепления
изучаемого материала, вы можете посмотреть видео – урок, пройдя по
ссылке
https://infourok.ru/videouroki/1511