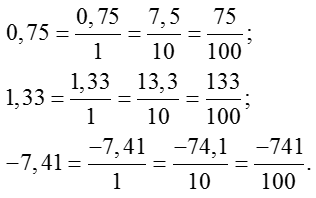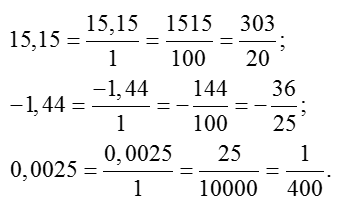Как перевести десятичную дробь в обыкновенную
1 января 2017
Вот, казалось бы, перевод десятичной дроби в обычную — элементарная тема, но многие ученики её не понимают! Поэтому сегодня мы подробно рассмотрим сразу несколько алгоритмов, с помощью которых вы разберётесь с любыми дробями буквально за секунду.
Напомню, что существует как минимум две формы записи одной и той же дроби: обыкновенная и десятичная. Десятичные дроби — это всевозможные конструкции вида 0,75; 1,33; и даже −7,41. А вот примеры обыкновенных дробей, которые выражают те же самые числа:
[0,75=frac{3}{4};quad 1,33=1frac{33}{100};quad -7,41=-7frac{41}{100}]
Сейчас разберёмся: как от десятичной записи перейти к обычной? И самое главное: как сделать это максимально быстро?
Основной алгоритм
На самом деле существует как минимум два алгоритма. И мы сейчас рассмотрим оба. Начнём с первого — самого простого и понятного.
Чтобы перевести десятичную дробь в обыкновенную, необходимо выполнить три шага:
- Переписать исходную дробь в виде новой дроби: в числителе останется исходная десятичная дробь, а в знаменателе нужно поставить единицу. При этом знак исходного числа также помещается в числитель. Например:
[0,75=frac{0,75}{1};quad 1,33=frac{1,33}{1};quad -7,41=frac{-7,41}{1}]
- Умножаем числитель и знаменатель полученной дроби на 10 до тех пор, пока в числителе не исчезнет запятая. Напомню: при каждом умножении на 10 запятая сдвигается вправо на один знак. Разумеется, поскольку знаменатель тоже умножается, там вместо числа 1 будут появляться 10, 100 и т.д. Примеры:
Алгоритм перехода к обычным дробям - Наконец, сокращаем полученную дробь по стандартной схеме: делим числитель и знаменатель на те числа, которым они кратны. Например, в первом примере 0,75=75/100, при этом и 75, и 100 делятся на 25. Поэтому получаем $0,75=frac{75}{100}=frac{3cdot 25}{4cdot 25}=frac{3}{4}$ — вот и весь ответ.:)
Важное замечание по поводу отрицательных чисел. Если в исходном примере перед десятичной дробью стоит знак «минус», то и на выходе перед обыкновенной дробью тоже должен стоять «минус». Вот ещё несколько примеров:
Особое внимание хотелось бы обратить на последний пример. Как видим, в дроби 0,0025 присутствует много нулей после запятой. Из-за этого приходится аж целых четыре раза умножать числитель и знаменатель на 10. Можно ли как-то упростить алгоритм в этом случае?
Конечно, можно. И сейчас мы рассмотрим альтернативный алгоритм — он чуть более сложен для восприятия, но после небольшой практики работает намного быстрее стандартного.
Более быстрый способ
В данном алгоритме также 3 шага. Чтобы получить обычную дробь из десятичной, нужно выполнить следующее:
- Посчитать, сколько цифр стоит после запятой. Например, у дроби 1,75 таких цифр две, а у 0,0025 — четыре. Обозначим это количество буквой $n$.
- Переписать исходное число в виде дроби вида $frac{a}{{{10}^{n}}}$, где $a$ — это все цифры исходной дроби (без «стартовых» нулей слева, если они есть), а $n$ — то самое количество цифр после запятой, которое мы посчитали на первом шаге. Другими словами, необходимо разделить цифры исходной дроби на единицу с $n$ нулями.
- По возможности сократить полученную дробь.
Вот и всё! На первый взгляд, эта схема сложнее предыдущей. Но на самом деле он и проще, и быстрее. Судите сами:
[0,64=frac{64}{100}=frac{16}{25}]
Как видим, в дроби 0,64 после запятой стоит две цифры — 6 и 4. Поэтому $n=2$. Если убрать запятую и нули слева (в данном случае — всего один ноль), то получим число 64. Переходим ко второму шагу: ${{10}^{n}}={{10}^{2}}=100$, поэтому в знаменателе стоит именно сто. Ну а затем остаётся лишь сократить числитель и знаменатель.:)
Ещё один пример:
[0,004=frac{4}{1000}=frac{1}{250}]
Здесь всё чуть сложнее. Во-первых, цифр после запятой уже 3 штуки, т.е. $n=3$, поэтому делить придётся на ${{10}^{n}}={{10}^{3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.
Наконец, последний пример:
[1,88=frac{188}{100}=frac{47}{25}=frac{25+22}{25}=1frac{22}{25}]
Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся.
Что делать с целой частью
На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.
Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется:
[0,88=frac{88}{100}=frac{22}{25}]
Затем вспоминаем про «утерянную» единицу и дописываем её спереди:
[frac{22}{25}to 1frac{22}{25}]
Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:
[begin{align}& 2,15to 0,15=frac{15}{100}=frac{3}{20}to 2frac{3}{20}; \& 13,8to 0,8=frac{8}{10}=frac{4}{5}to 13frac{4}{5}. \end{align}]
В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)
В заключение хотел бы рассмотреть ещё один приём, который многим помогает.
Преобразования «на слух»
Давайте задумаемся о том, что вообще такое десятичная дробь. Точнее, как мы её читаем. Например, число 0,64 — мы читаем его как «ноль целых, 64 сотых», правильно? Ну, или просто «64 сотых». Ключевое слово здесь — «сотых», т.е. число 100.
А что насчёт 0,004? Это же «ноль целых, 4 тысячных» или просто «четыре тысячных». Так или иначе, ключевое слово — «тысячных», т.е. 1000.
Ну и что в этом такого? А то, что именно эти числа в итоге «всплывают» в знаменателях на втором этапе алгоритма. Т.е. 0,004 — это «четыре тысячных» или «4 разделить на 1000»:
[0,004=4:1000=frac{4}{1000}=frac{1}{250}]
Попробуйте потренироваться сами — это очень просто. Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому
[2,5=2frac{5}{10}=2frac{1}{2}]
А какое-нибудь 1,125 — это «1 целая, 125 тысячных», поэтому
[1,125=1frac{125}{1000}=1frac{1}{8}]
В последнем примере, конечно, кто-то возразит, мол, не всякому ученику очевидно, что 1000 делится на 125. Но здесь нужно помнить, что 1000 = 103, а 10 = 2 ∙ 5, поэтому
[begin{align}& 1000=10cdot 10cdot 10=2cdot 5cdot 2cdot 5cdot 2cdot 5= \& =2cdot 2cdot 2cdot 5cdot 5cdot 5=8cdot 125end{align}]
Таким образом, любая степень десятки раскладывается лишь на множители 2 и 5 — именно эти множители нужно искать и в числителе, чтобы в итоге всё сократилось.
На этом урок окончен. Переходим к более сложной обратной операции — см. «Переход от обыкновенной дроби к десятичной».
Смотрите также:
- Сравнение дробей
- Периодические десятичные дроби
- Тригонометрические функции
- Что такое числовая дробь
- Задачи на проценты считаем проценты с помощью формулы
- Более сложные задачи на производительность
Перейти к содержанию
Главная » АЛГЕБРА » Обращение десятичной дроби в обыкновенную
Обращение десятичной дроби в обыкновенную
Опубликовано 25.06.2022
Как перевести десятичную дробь в обыкновенную? Чтобы из десятичной дроби сделать обыкновенную, достаточно в числителе дроби записать число, стоящее после запятой, а в знаменателе – единицу с нулями, причем нулей должно быть столько, сколько цифр справа от запятой (в дробной части десятичной дроби).
Например, ,
.
Это все равно, что записать десятичную дробь таким образом:
.
Примеры перевода дробей
Еще больше примеров как из десятичной дроби сделать обыкновенную. Давайте практиковаться:
Зачем переводить десятичную дробь в обыкновенную
Для чего это нужно? Иногда в одном задании на нахождение значения выражения встречаются и обыкновенные и десятичные дроби. Поэтому бывает нужно сделать из десятичной дроби обыкновенную.
Например, необходимо найти значение выражения:
.
Можно перевести обыкновенную дробь в десятичную, или десятичную в обыкновенную, смотря какие нам даны дроби и как удобнее поступить.
Запишем,
.
Еще один пример. Найдите значение выражения:
.
Удобнее представить десятичные дроби в виде обыкновенных дробей:
=
=
.
Интересные статьи по алгебре:
( 1 оценка, среднее 5 из 5 )
Перевод дробей
- Главная
- /
- Математика
- /
- Арифметика
- /
- Перевод дробей
Если вам необходимо перевести десятичную дробь в обыкновенную или наоборот воспользуйтесь нашим онлайн калькулятором:
Перевод обыкновенной дроби в десятичную
Перевод десятичной дроби в обыкновенную
Просто заполните необходимые поля и получите ответ и подробное решение.
Теория
Как перевести обыкновенную дробь в десятичную
Чтобы перевести обыкновенную дробь в десятичную дробь нужно числитель разделить на знаменатель и к полученному числу прибавить целую часть (если она есть).
Формула
a bc = a + b : c
Пример
Для примера преобразуем следующую дробь:
5 12 = 5 + 1 : 2 = 5 + 0.5 = 5.5
Как перевести десятичную дробь в обыкновенную
Чтобы перевести десятичную дробь в обыкновенную дробь необходимо все цифры после запятой поместить в числитель, а знаменатель будет состоять из единицы и такого количества нулей, сколько цифр в числителе. При этом целая часть числа остаётся неизменной, а полученную дробь нужно сократить, если это возможно.
Примеры
Для примера переведём 5.5 в обыкновенную дробь, а точнее в смешанное число:
5.5 = 5510=55 : 510 : 5=512
Ещё пара примеров:
0.06 = 6100= 6 : 2100 : 2= 350
1.001 = 111000
См. также
Перевести десятичную дробь в обыкновенную
Как перевести десятичную дробь в обыкновенную
В числитель записываем саму десятичную дробь, в знаменатель 1. Домножим и числитель и знаменатель на множитель равный 1 с количеством нулей таким же как в исходной десятичной дроби чисел после запятой. При необходимости сократим дробь.
Разберём пример. Переведём десятичную дробь 0.75 в обыкновенную. Запишем в числителе 0.75 а в знаменателе 1 — 0.75/. Чтобы избавиться от дробной части домножим числитель и знаменатель на 100 — получится 0.75/1 = 75/100. Сократим дробь 75/100 = 3/4
Похожие калькуляторы
Перевести десятичную дробь в обыкновенную дробь
- Математика
- Дроби
- Преобразовать десятичную дробь
Калькулятор
онлайн преобразования десятичных дробей
Обыкновенную
в десятичную
Калькулятор покажет как перевести десятичную дробь в обыкновенную дробь, либо в смешанное
число. Введите десятичную дробь и калькулятор напишет подробное решение.
Перевод десятичных дробей в обыкновенные дроби
Алгоритм преобразования
Чтобы преобразовать десятичную дробь в обыкновенную
дробь нужно выполнить следующие шаги:
-
1 Записать в виде дроби с знаменателем
1: -
2 Умножать числить и знаменатель на
10 за каждый знак после запятой десятичной дроби. Например для
десятичной дроби 0.025 нужно умножить 3 раза на 10, т.к. 3 цифры после запятой.
Иначе говоря умножаем на 10 пока числитель не станет целым числом. -
3 Упростить(сократить) полученную дробь.
Чтобы сократить дробь нужно найти наибольший общий делитель числителя и знаменателя
дроби.
Рассмотрим на примере числа 0.025 как перевести десятичную дробь в
обыкновенную.
Пример Преобразования числа 0.025 в дробь
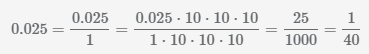
НОД(25,1000)=25.
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное
число, то получится равная ей дробь.
Примеры преобразования десятичных дробей
Перевод десятичной дроби в обыкновенную дробь
Рассмотрим на примерах процесс преобразования десятичных дробей.
Пример Преобразовать десятичную дробь 0.45
в обыкновенную дробь
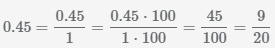
Сократим дробь 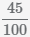
помощью нахождения наибольшего общего делителя числителя и знаменателя и
последующего деления полученного числа на числитель и знаменатель, НОД(45,100)=5.
Пример Преобразовать 0.875 в дробь.
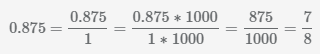
НОД(875,1000)=125
Перевод десятичной дроби в смешанную дробь
Если десятичная дробь больше 1, то в результате преобразования получается смешанное
число. Целая часть при переводе остается неизменной.
Рассмотрим на примере как переводить число в смешанную дробь.
Пример Преобразовать число 567.35 в
смешанное число
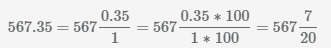
В результат преобразования получаем смешанную дробь.
Пример Перевести число 1.99 в дробь
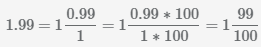
Другие переводы дробей.
Смотрите также
Другие страницы