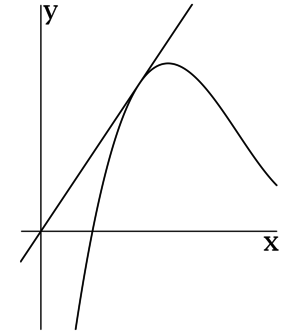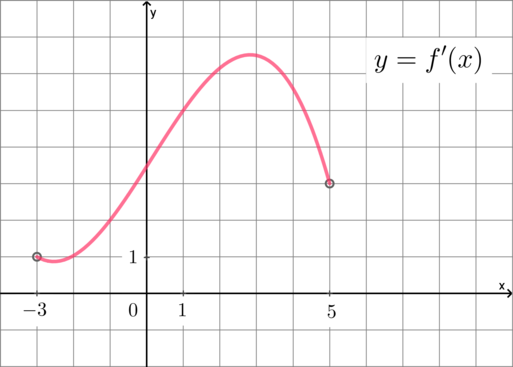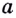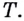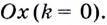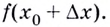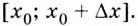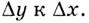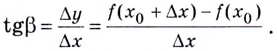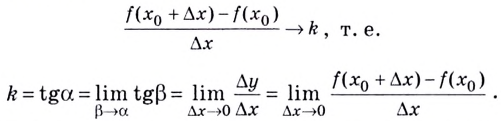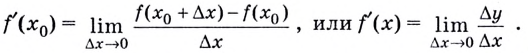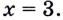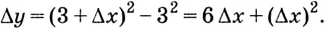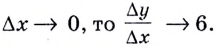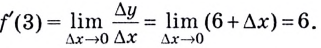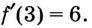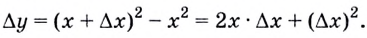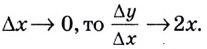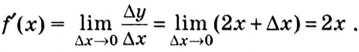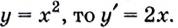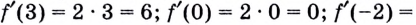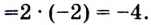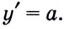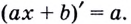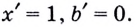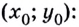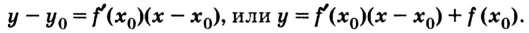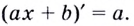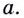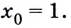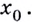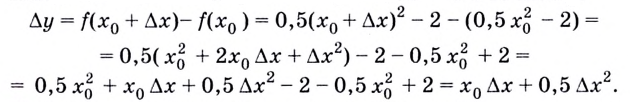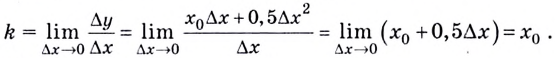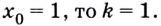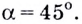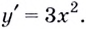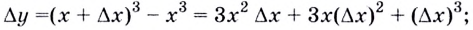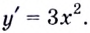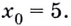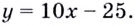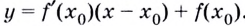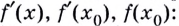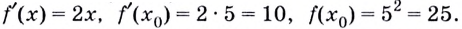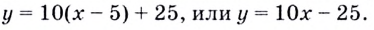Геометрический смысл производной
Если плохо разбираешься в производной, то вот тебе полноценный гид по ней, с текстом, примерами и вебинарами: «Производная функции – геометрический смысл и правила дифференцирования»!
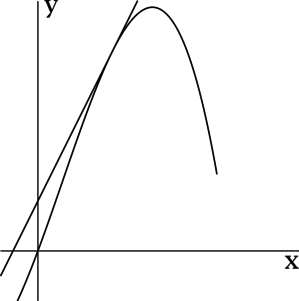
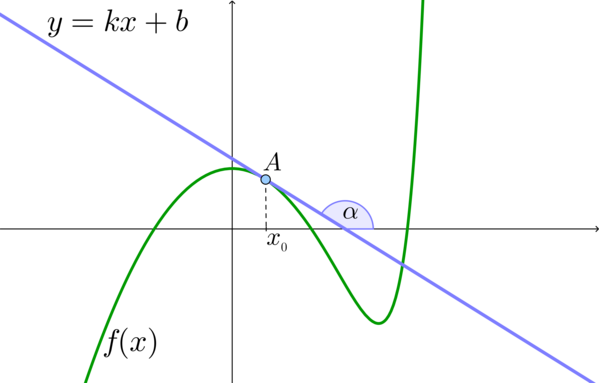
Рассмотрим график какой-то функции ( y=fleft( x right)):
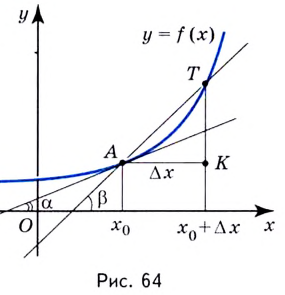
Выберем на линии графика некую точку ( A). Пусть ее абсцисса ( {{x}_{0}}), тогда ордината равна ( fleft( {{x}_{0}} right)).
Затем выберем близкую к точке ( A) точку ( B) с абсциссой ( {{x}_{0}}+Delta x); ее ордината – это ( fleft( {{x}_{0}}+Delta x right)):
Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии).
Обозначим угол наклона прямой к оси ( Ox) как ( alpha ).
Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.
Какие значения может принимать угол ( alpha )?
Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – ( 180{}^circ ), а минимально возможный – ( 0{}^circ ).
Значит, ( alpha in left[ 0{}^circ ;180{}^circ right)). Угол ( 180{}^circ ) не включается, поскольку положение прямой в этом случае в точности совпадает с ( 0{}^circ ), а логичнее выбирать меньший угол.
Возьмем на рисунке такую точку ( C), чтобы прямая ( AC) была параллельна оси абсцисс, а ( BC) – ординат:
По рисунку видно, что ( AC=Delta x), а ( BC=Delta f).
Тогда отношение приращений:
( frac{Delta f}{Delta x}=frac{BC}{AC}={tg}alpha )
(так как ( angle C=90{}^circ ), то ( triangle ABC) – прямоугольный).
Давай теперь уменьшать ( Delta x).
Тогда точка ( B) будет приближаться к точке ( A). Когда ( Delta x) станет бесконечно малым ( left( Delta xto 0 right)), отношение ( frac{Delta f}{Delta x}) станет равно производной функции в точке ( {{x}_{0}}).
Что же при этом станет с секущей?
Точка ( B) будет бесконечно близка к точке ( A), так что их можно будет считать одной и той же точкой.
Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки ( A), но этого достаточно).
Говорят, что при этом секущая занимает предельное положение.
Угол наклона секущей к оси ( displaystyle Ox) назовем ( varphi ). Тогда получится, что производная
( {f}’left( {{x}_{0}} right)underset{Delta xto 0}{mathop{=}},frac{Delta f}{Delta x}= {tg}varphi ),
то есть
Производная равна тангенсу угла наклона касательной к графику функции в данной точке
Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:
( y=kx+b).
За что отвечает коэффициент ( displaystyle k)? За наклон прямой. Он так и называется: угловой коэффициент.
Что это значит? А то, что равен он тангенсу угла между прямой и осью ( displaystyle Ox)!
То есть вот что получается:
( {f}’left( {{x}_{0}} right)= {tg}varphi =k).
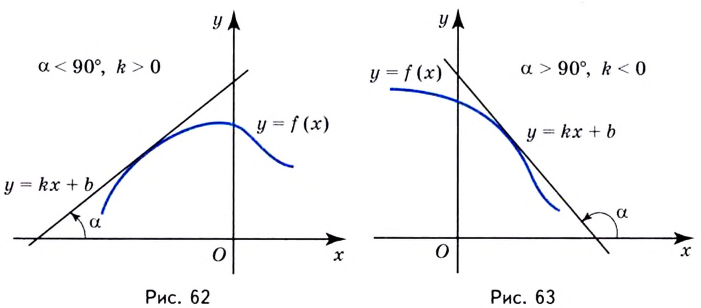
Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей?
Посмотрим: Теперь углы ( alpha ) и ( displaystyle varphi ) тупые. А приращение функции ( Delta f) – отрицательное.
Снова рассмотрим ( triangle ABC): ( angle B=180{}^circ -alpha text{ }Rightarrow text{ } {tg}angle B=- {tg}alpha ).
С другой стороны, ( {tg}angle B=frac{AC}{BC}=frac{-Delta f}{Delta x}).
Получаем: ( frac{-Delta f}{Delta x}=- {tg}alpha text{ }Rightarrow text{ }frac{Delta f}{Delta x}= {tg}alpha ), то есть все, как и в прошлый раз.
Снова устремим точку ( displaystyle B) к точке ( displaystyle A), и секущая ( displaystyle AB) примет предельное положение, то есть превратится в касательную к графику функции в точке ( displaystyle A).
Итак, сформулируем окончательно полученное правило:
Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:
( {f}’left( {{x}_{0}} right)= {tg}varphi =k)
Это и есть геометрический смысл производной.
Окей, все это интересно, но зачем оно нам? Вот пример:
На рисунке изображен график функции ( displaystyle y=mathsf{f}left( x right)) и касательная к нему в точке с абсциссой ( {{x}_{0}}).
Найдите значение производной функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}).
Решение.
Как мы недавно выяснили, значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:
( displaystyle f’left( x right)=k= {tg}varphi).
Значит, для нахождения значения производной нам нужно найти тангенс угла наклона касательной.
На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!
Угол наклона касательной к оси ( displaystyle Ox) – это ( displaystyle angle BAC). Найдем тангенс этого угла:
( displaystyle {tg}angle BAC=frac{BC}{AC}=frac{6}{5}=1,2).
Таким образом, производная функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}) равна ( displaystyle 1,2).
Ответ: ( displaystyle 1,2).
Теперь попробуй сам.
Уравнение касательной к графику функций
А сейчас сосредоточимся на произвольных касательных.
Предположим, у нас есть какая-то функция, например, ( fleft( x right)=left( {{x}^{2}}+2 right)). Мы нарисовали ее график и хотим провести касательную к нему в какой-нибудь точке ( {{x}_{0}}). Например, в точке ( {{x}_{0}}=2).
Берем линейку, пристраиваем ее к графику и чертим:
Что мы знаем об этой прямой? Что самое важное нужно знать о прямой на координатной плоскости?
Поскольку прямая – это изображение линейной функции, очень удобно было бы знать ее уравнение. То есть коэффициенты ( k) и ( b) в уравнении
( y=kx+b).
Но ведь ( k) мы уже знаем! Это угловой коэффициент касательной, который равен производной функции в этой точке:
( k={f}’left( {{x}_{0}} right)).
В нашем примере будет так:
( {f}’left( x right)={{left( {{x}^{2}}+2 right)}^{prime }}=2x;)
( k={f}’left( {{x}_{0}} right)={f}’left( 2 right)=2cdot 2=4.)
Теперь остается найти ( b) . Это проще простого: ведь ( b) – значение ( y) при ( displaystyle x=0).
Графически ( b) – это координата пересечения прямой с осью ординат (ведь ( displaystyle x=0) во всех точках оси ( displaystyle Oy)):
Проведём ( BCparallel Ox) (так, что ( triangle ABC) – прямоугольный).
Тогда ( angle ABC=alpha )(тому самому углу между касательной и осью абсцисс). Чему равны ( displaystyle AC) и ( displaystyle BC)?
По рисунку явно видно, что ( BC={{x}_{0}}), а ( AC=fleft( {{x}_{0}} right)-b). Тогда получаем:
( {f}’left( {{x}_{0}} right)= {tg}alpha =frac{AC}{BC}=frac{fleft( {{x}_{0}} right)-b}{{{x}_{0}}}text{ }Rightarrow text{ }b=fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right)).
Соединяем все полученные формулы в уравнение прямой:
( y=kx+b={f}’left( {{x}_{0}} right)cdot x+fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right);)
( y={f}’left( {{x}_{0}} right)cdot left( x-{{x}_{0}} right)+fleft( {{x}_{0}} right))
Это и есть уравнение касательной к графику функции ( fleft( x right)) в точке ( {{x}_{0}}).
Пример:
Найди уравнение касательной к графику функции ( fleft( x right)={{x}^{2}}-2x+3) в точке ( {{x}_{0}}=3).
Решение:
На этом примере выработаем простой…
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
ЕГЭ №7. Производная функции — геометрический смысл, дифференцирование
На этом видео мы вспомним, что такое функция и её график, научимся искать производную некоторых функций, например, такой: y = 2×3 – 3×2 + x + 5.
Мы разберём от А до Я все 7 типов задач, которые могут попасться в задаче №7 из ЕГЭ. Узнаем, на какие 3 фразы в условии задачи нужно обратить особое внимание, чтобы с лёгкостью решить задачу и не потерять баллы на ровном месте.
Разберём все возможные ошибки, которые можно допустить в этих задачах. Мы поймём, что многие из этих задач решаются обычным подсчётом клеточек на графике! Главное – не перепутать, что нужно считать.
P.S. Не забудьте потом посмотреть родственную тему: «Интегралы на ЕГЭ. Первообразные элементарных функций».
Тема 7.
Взаимосвязь функции и ее производной
7
.
03
Производная в точке касания как угловой коэффициент касательной
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
взаимосвязь функции и ее производной
Решаем задачи
Прямая, заданная уравнением касается графика функции
в точке
Найдите
Прямая, заданная уравнением касается графика функции
в точке
Найдите
Друзья, поздравляем вас с Новым годом! Этот новогодний пробный вариант ЕГЭ подготовлен специально для вас, и, прорешав все задачи правильно, вы можете получить секретный код. Числу, составленному из цифр каждого ответа, соответствует буква в русском алфавите. Тогда правильные ответы ко всем задачам помогут вам составить фразу, которую мы загадали. Введите ее в поле ответа к заданию 19 без пробелов с маленькой буквы.
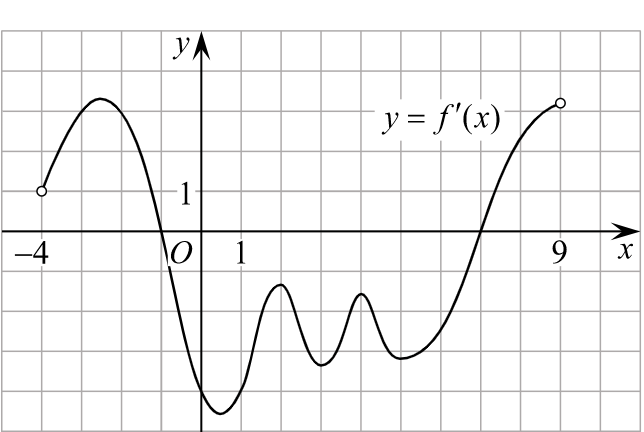
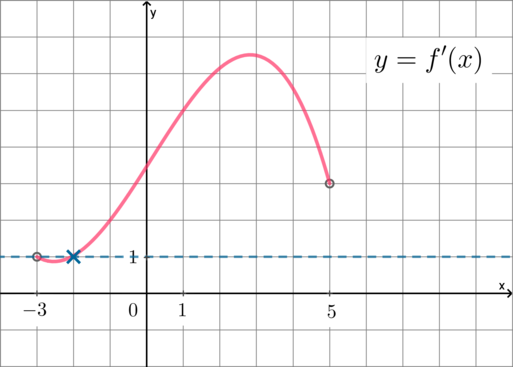
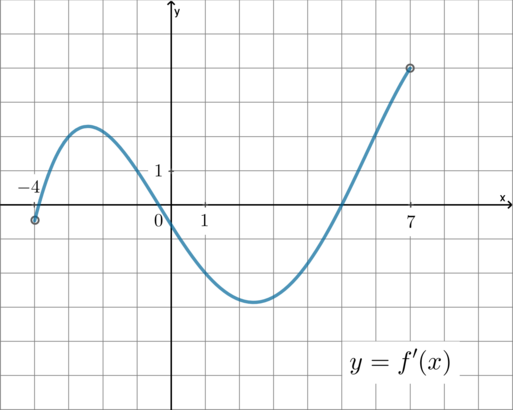
На рисунке изображён график — производной функции
определённой на интервале Найдите количество точек, в которых
касательная к графику функции параллельна прямой
или
совпадает с ней.
На рисунке изображен график производной функции определенной на интервале
Найдите количество точек, в
которых касательная к графику функции параллельна прямой
или совпадает с ней.
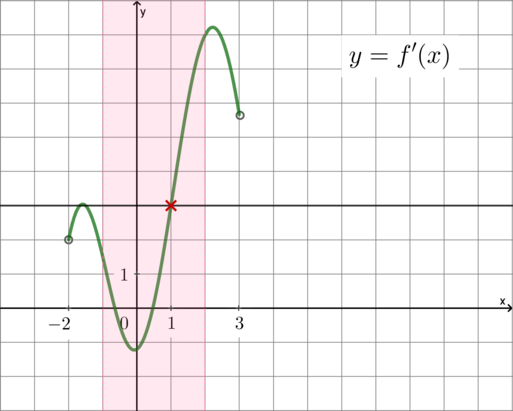
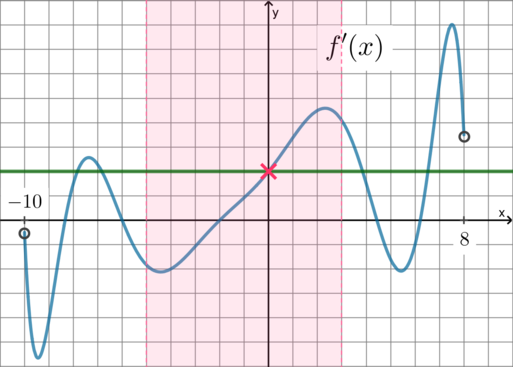
На рисунке изображен график — производной функции
, определенной на интервале
. Найдите
абсциссу точки касания графика функции и прямой, параллельной прямой
или совпадающей с ней.
Показать ответ и решение
Если касательная параллельна прямой , то угловой коэффициент касательной равен угловому коэффициенту прямой
,
следовательно, .
Так как , где
— точка касания, и на рисунке изображен график производной, то на графике производной
нужно найти абсциссу точки, в которой , то есть ордината равна
.
Заметим, что в точке производная не определена, так как в условии задачи сказано, что она определена на интервале
Тогда подходит
Показать ответ и решение
Если касательная параллельна прямой то угловой коэффициент
касательной равен угловому коэффициенту прямой
следовательно,
Так как где
— абсцисса точки касания, и на рисунке изображен график производной, то на графике
производной нужно найти точку, для которой то есть ордината равна 3.
Также нужно учесть, что абсцисса этой точки должна быть из отрезка Следовательно, это
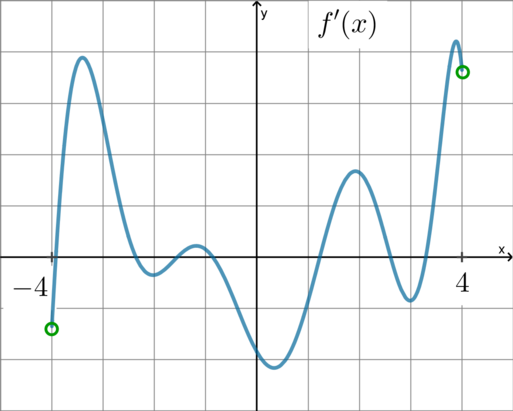
На рисунке изображен график — производной функции
, определенной на интервале
. Найдите
количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.
Показать ответ и решение
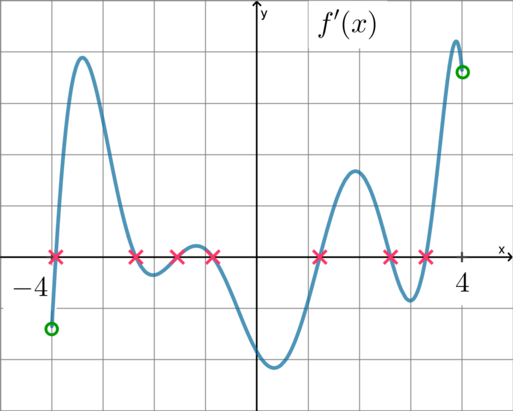
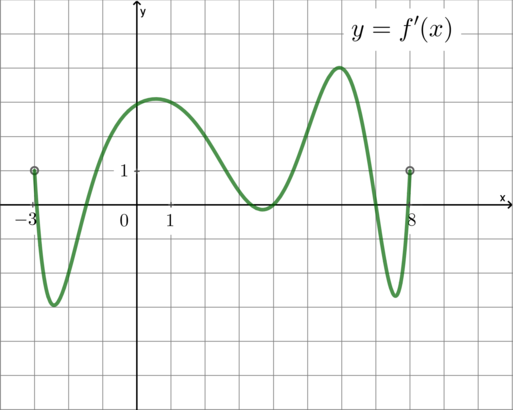
Так как на рисунке изображен график производной, то нужно свести условие задачи к какому-то условию на производную.
Если касательная параллельна прямой
, то их угловые коэффициенты равны. Следовательно, угловой коэффициент
касательной равен 0: , где
— некоторое число.
Если — касательная к графику
, то ее угловой коэффициент равен
, где
— абсцисса точки касания.
Количество этих точек нам и нужно найти. Следовательно, .
Итак, мы свели условие задачи к производной. Как найти , если мы знаем, что
? Это значит, что нам нужно найти
точку на графике , у которой ордината равна 0. Таких точек 7.
Показать ответ и решение
Так как на рисунке изображен график производной, то нужно свести условие задачи к какому-то условию на производную.
Если касательная параллельна прямой
, то их угловые коэффициенты равны. Следовательно, угловой
коэффициент касательной равен 2: , где
— некоторое число.
Если — касательная к графику
, то ее угловой коэффициент равен
, где
— абсцисса точки касания, которую
и нужно найти. Следовательно, .
Итак, мы свели условие задачи к производной. Как найти , если мы знаем, что
? Это значит, что нам нужно найти
точку на графике , у которой ордината равна 2, и определить абсциссу этой точки. Учитывая, что эта точка должна
находиться на отрезке , то она одна и ее абсцисса равна 0.
На рисунке изображен график — производной функции
определенной на интервале
Найдите
количество точек, в которых касательная к графику функции перпендикулярна прямой
На рисунке изображен график — производной функции
определенной на интервале Найдите угловой коэффициент касательной,
проведенной к графику функции в точке с абсциссой 1.
Показать ответ и решение
Угловой коэффициент касательной, проведенной к графику функции в
точке с абсциссой равен значению производной в точке касания, то есть равен
Следовательно, нам нужно найти
Таким образом, на графике
нужно найти точку, абсцисса которой равна 1, и определить ее ординату. Отметим
эту точку:
Следовательно,
На рисунке изображен график — производной функции
определенной на интервале
Найдите количество
точек, в которых касательная к графику функции параллельна прямой
или совпадает с ней.
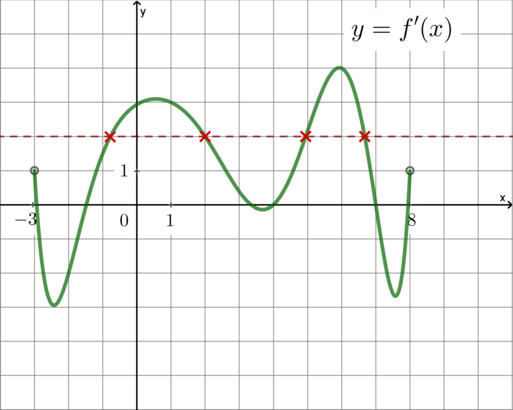
Показать ответ и решение
Если касательная параллельна прямой то угловой коэффициент касательной равен угловому коэффициенту прямой
следовательно,
Так как где
— точка касания, и на рисунке изображен график производной, то на графике
производной нужно найти количество таких точек, в которых то есть ордината равна 2. Таких точек 4.
Показать ответ и решение
Производная функции в точке
равна угловому коэффициенту касательной, то
есть
Значит, так как , то
, откуда
.
Вы уже знаете, какую прямую называют касательной к окружности. А что понимают, например, под касательной к синусоиде? Прямая
Пусть даны график функции 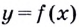
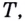
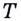
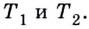
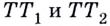
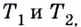
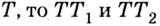
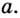
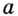
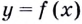
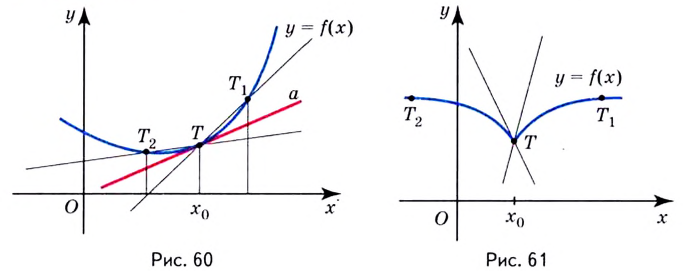
Если график функции такой, как показано на рисунке 61, то при неограниченном приближении точек 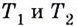
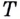
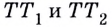
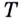
И если 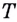
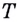
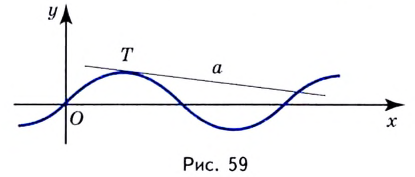
Понятие касательной к графику часто используют для исследования функций. Рассмотрим этот вопрос сначала в общем виде.
Касательная — это прямая. Её уравнение имеет вид 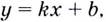
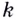
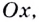
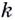
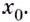
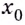
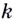
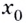
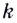
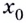
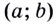
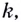
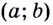
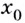
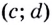
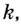
Итак, зная угловые коэффициенты касательных к графику функции в тех или иных точках, можно сделать вывод, возрастает данная функция в этих точках, или убывает.
Поскольку для исследования функций важно уметь определять угловой коэффициент касательной к её графику, то рассмотрим подробнее связь этого коэффициента с исследуемой функцией.
Пусть даны график функции 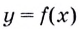
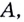
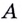
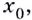
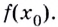
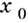
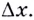
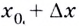
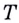
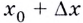
Через точки 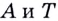
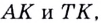
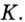
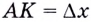
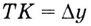
Угловой коэффициент секущей 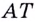
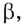
Если 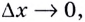
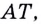
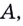
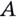
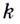
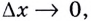
Так определяется угловой коэффициент касательной к графику функции 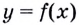
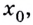
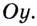
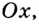
К вычислению значения выражения 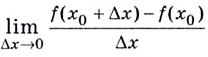
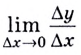
Производной функции 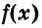
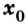
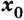
Производную функции 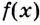
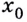
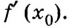
Пример:
Найдите производную функции 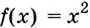
Решение:
Дадим аргументу 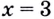
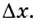
Тогда 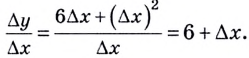
Следовательно,
Ответ.
Так решают задачу, пользуясь определением производной функции в точке.
До сих пор речь шла о производной функции в точке. А можно рассматривать производную функции и как функцию. Пусть, например, дана функция 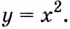
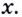
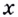
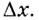
Поэтому 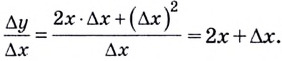
Имеем
Следовательно, производная функции 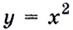
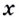
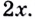
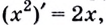
Обратите внимание! Производная функции в точке — это число. Когда же говорят о производной, не указывая «в точке», подразумевают производную как функцию: производной функции 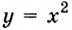
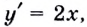
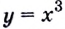
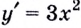
Зная это, производную функции в точке можно вычислять проще, чем по определению производной функции в точке. Пример 2. Дана функция 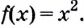
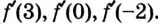
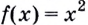
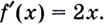
Нахождение производной называется дифференцированием. Функция, которая имеет производную в точке 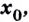
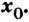
Докажем, например, что линейная функция 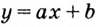
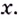
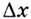
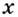
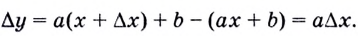
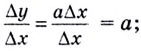
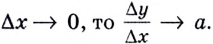
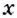
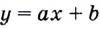
Пишут
В частности:
Производная постоянной равна нулю.
Из курса планиметрии известно, что уравнение прямой, проходящей через заданную точку 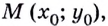
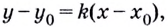
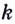
Поскольку для касательной к графику функции 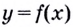
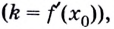
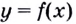
До сих пор речь шла о касательных к криволинейным графикам. Но графиком функции может быть и прямая или часть прямой. Поэтому для обобщения договариваются касательной к прямой в любой её точке считать эту самую прямую. Касательной к отрезку или лучу в любой его внутренней точке считают прямую, которой принадлежит этот отрезок или луч.
Выше было установлено, что производная линейной функции равна коэффициенту при переменной, т.е
Полученный результат имеет очевидный геометрический смысл: касательная к прямой — графику функции 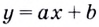
- Заказать решение задач по высшей математике
Пример:
Найдите угол, который образуете положительным направлением оси 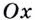
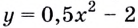
Решение:
Определим сначала угловой коэффициент этой касательной по формуле 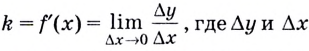
Найдем приращение функции 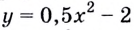
Найдём угловой коэффициент касательной:
Поскольку
Известно также, что 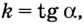
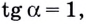
Пример:
Докажите, что для функции 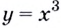
Решение:
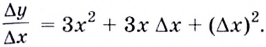
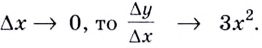
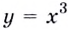
Пример:
Напишите уравнение касательной к графику функции 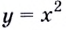
Решение:
Способ 1. Уравнение касательной имеет вид 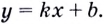
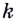
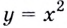
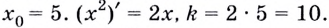
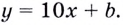
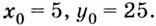
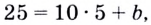
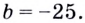
Способ 2. Запишем общий вид уравнения касательной:
Найдём
Подставим найденные значения в уравнение касательной:
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности
- Применение производной к исследованию функции
- Иррациональные неравенства
- Производная в математике
- Как найти производную функции
- Асимптоты графика функции
п.1. Уравнение касательной
Рассмотрим кривую (y=f(x)).
Выберем на ней точку A с координатами ((x_0,y_0)), проведем касательную AB в этой точке.
Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке (x_0): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: ((y_B-y_A)=k(x_B-x_A)).
Для (A(x_0,y_0), B(x,y)) получаем: begin{gather*} (y-y_0)=k(x-x_0)\ y=k(x-x_0)+y_0\ y=f'(x_0)(x-x_0)+f(x_0) end{gather*}
Уравнение касательной к кривой (y=f(x)) в точке (x_0) имеет вид: $$ y=f'(x_0)(x-x_0)+f(x_0) $$ при условии, что производная (f'(x_0)=aneinfty) — существует и конечна.
Чтобы записать уравнение касательной с угловым коэффициентом в виде (y=kx+b), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=underbrace{f'(x_0)}_{=k}x+underbrace{f(x_0)-f'(x_0)cdot x_0}_{=b} $$
Уравнение касательной с угловым коэффициентом: begin{gather*} y=kx+b\ k=f'(x_0), b=f(x_0)-f'(x_0)cdot x_0 end{gather*}
п.2. Алгоритм построения касательной
На входе: уравнение кривой (y=f(x)), абсцисса точки касания (x_0).
Шаг 1. Найти значение функции в точке касания (f(x_0))
Шаг 2. Найти общее уравнение производной (f’ (x))
Шаг 3. Найти значение производной в точке касания (f'(x_0 ))
Шаг 4. Записать уравнение касательной (y=f’ (x_0)(x-x_0)+f(x_0)), привести его к виду (y=kx+b)
На выходе: уравнение касательной в виде (y=kx+b)
Например:
 |
Пусть (f(x)=x^2+3). Найдем касательную к этой параболе в точке (x_0=1). (f(x_0)=1^2+3=4 ) |
п.3. Вертикальная касательная
В случае, если производная (f'(x_0)=pminfty) — существует, но бесконечна, в точке (x_0) проходит вертикальная касательная (x=x_0).
Внимание!
Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода (x_0notin D), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку (x_0in D), входящую в область определения. График функции и касательная имеют одну общую точку ((x_0,y_0)).
Вертикальные касательные характерны для радикалов вида (y=sqrt[n]{x}).
Например:
 |
Пусть (f(x)=sqrt[5]{x-1}+1). Найдем касательную к этой кривой в точке (x_0=1). (f(x_0)=sqrt[5]{1-1}+1=1) |
п.4. Примеры
Пример 1. Для функции (f(x)=2x^2+4x)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.
 |
Находим точки пересечения, решаем уравнение: $$ 2x^2+4x=0Rightarrow 2x(x+2)=0Rightarrow left[ begin{array}{l} x=0\ x=-2 end{array} right. $$ Две точки на оси: (0;0) и (-2;0). Касательная в точке (x_0=0): begin{gather*} f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot 0+4=4\ y=4(x-0)+0=4x end{gather*} Касательная в точке (x_0=-2): begin{gather*} f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot (-2)+4=-4\ y=-4(x+2)+0=-4x-8 end{gather*} |
б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.
 |
Общее уравнение касательной: (f'(x)=4x+4) По условию (f'(x_0)=tgalpha=tg45^circ=1) Решаем уравнение: $$ 4x_0+4=1Rightarrow 4x_0=-3Rightarrow x_0=-frac34 $$ Точка касания (x_0=-frac34) begin{gather*} f(x_0)=2cdotleft(-frac34right)^2+4cdotleft(-frac34right)=frac98-3=-frac{15}{8} end{gather*} Уравнение касательной: begin{gather*} y=1cdotleft(x+frac34right)-frac{15}{8}=x-frac98 end{gather*} |
в) найдите, в какой точке касательная будет параллельна прямой (2x+y-6=0). Напишите уравнение этой касательной.
 |
Найдем угловой коэффициент заданной прямой: (y=-2x+6Rightarrow k=-2). Касательная должна быть параллельной, значит, её угловой коэффициент тоже (k=-2). Получаем уравнение: begin{gather*} f'(x_0)=-2\ 4x_0+4=-2Rightarrow 4x_0=-6Rightarrow x_0=-frac32 end{gather*} Точка касания (x_0=-frac32) begin{gather*} f(x_0)=2cdotleft(-frac32right)^2+4cdotleft(-frac32right)=\ =frac92-6=-frac32 end{gather*} Уравнение касательной: begin{gather*} y=-2cdotleft(x+frac32right)-frac32=-2x-frac92 end{gather*} Или, в каноническом виде: begin{gather*} 2x+y+frac92=0 end{gather*} |
г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.
 |
У горизонтальной прямой (k=0). Получаем уравнение: (f'(x_0)=0). begin{gather*} 4x_0+4=0Rightarrow 4x_0=-4Rightarrow x_0=-1 end{gather*} Точка касания (x_0=-1) begin{gather*} f(x_0)=2cdot(-1)^2+4cdot(-1)=-2 end{gather*} Уравнение касательной: begin{gather*} y=0cdot(x+1)-2=-2 end{gather*} |
Ответ: а) (y=4x) и (y=-4x-8); б) (y=x-frac98); в) (2x+y+frac92=0); г) (y=-2)
Пример 2. Напишите уравнение касательной к графику функции в заданной точке:
a) ( f(x)=frac5x+frac x5, x_0=4 ) begin{gather*} f(x_0)=frac54+frac45=frac{25+16}{20}=frac{41}{20}\ f'(x)=left(frac5xright)’+left(frac x5right)’=-frac{5}{x^2}+frac15=frac{-25+x^2}{5x^2}=frac{x^2-25}{5x^2}\ f'(x_0)=frac{4^2-25}{5cdot 4^2}=-frac{9}{80} end{gather*} Уравнение касательной: $$ y=-frac{9}{80}(x-4)+frac{41}{20}=-frac{9}{80}x+frac{9}{20}+frac{41}{20}=-frac{9}{80}x+2,5 $$
б) ( f(x)=frac{x^2+5}{3-x}, x_0=2 ) begin{gather*} f(x_0)=frac{2^2+5}{3-2}=frac91=9\ f'(x)=frac{(x^2+5)'(3-x)-(x^2+5)(3-x)’}{(3-x)^2}=frac{2x(3-x)+(x^2+5)}{(3-x)^2}=\ =frac{6x-2x^2+x^2+5}{(3-x)^2}=frac{-x^2+6x+5}{(3-x)^2}\ f'(x_0)=frac{-2^2+6cdot 2+5}{(3-2)^2}=13 end{gather*} Уравнение касательной: $$ y=13(x-2)+9=13x-26+9=13x-17 $$
Пример 3*. Найдите точку, в которой касательная к графику функции (f(x)=frac{x^2+2}{x+3}-x) перпендикулярна прямой (y=11x+3). Напишите уравнение этой касательной.
Угловой коэффициент данной прямой (k_1=11).
Угловой коэффициент перпендикулярной прямой (k_2=-frac{1}{k_1}=-frac{1}{11}) begin{gather*} f'(x)=left(frac{x^2+2}{x+3}right)’-x’=frac{2x(x+3)-(x^2+2)cdot 1}{(x+3)^2}-1=frac{2x^2+6x-x^2-2-(x+3)^2}{(x+3)^2}=\ =frac{x^2+6x-2-x^2-6x-9}{(x+3)^2}=- frac{11}{(x+3)^2} end{gather*} В точке касания: begin{gather*} f'(x_0)=k_2Rightarrow=-frac{11}{(x+3)^2}=-frac{1}{11}Rightarrow (x+3)^2=121Rightarrow (x+3)^2-11^2=0Rightarrow\ Rightarrow (x+14)(x+8)=0Rightarrow left[ begin{array}{l} x=-14\ x=8 end{array} right. end{gather*} 
Уравнение касательной при (x_0=-14) begin{gather*} f(x_0)=frac{(-14)^2+2}{-14+3}+14=frac{198}{-11}+14=-18+14=-4\ y=-frac{1}{11}(x+14)-4=-frac{x+58}{11} end{gather*} Уравнение касательной при (x_0=8) begin{gather*} f(x_0)=frac{8^2+2}{8+3}-8=frac{66}{11}-8=-2\ y=-frac{1}{11}(x-8)-2=-frac{x+14}{11} end{gather*}
Ответ: точка касания (-14;-4), уравнение (y=-frac{x+58}{11})
и точка касания (8;-2), уравнение (-frac{x+14}{11})
Пример 4*. Найдите уравнения общих касательных к параболам (y=x^2-5x+6) и (y=x^2+x+1). Укажите точки касания.
Найдем производные функций: begin{gather*} f_1′(x)=2x-5, f_2′(x)=2x+1 end{gather*} Пусть a – абсцисса точки касания для первой параболы, b — для второй.
Запишем уравнения касательных (g_1(x)) и (g_2(x)) через эти переменные. begin{gather*} g_1(x)=f_1′(a)(x-a)+f_1(a)=(2a-5)(x-a)+a^2-5a+6=\ =(2a-5)x-2a^2+5a+a^2-5a+6=(2a-5)x+(6-a^2)\ \ g_2(x)=f_2′(b)(x-b)+f_2(b)=(2b+1)(x-b)+b^2+b+1=\ =(2b+1)x-2b^2-b+b^2+b+1=(2b+1)x+(1-b^2) end{gather*} Для общей касательной должны быть равны угловые коэффициенты и свободные члены. Получаем систему уравнений: begin{gather*} begin{cases} 2a-5=2b+1\ 6-a^2=1-b^2 end{cases} Rightarrow begin{cases} 2(a-b)=6\ a^2-b^2=5 end{cases} Rightarrow begin{cases} a-b=3\ (a-b)(a+b)=5 end{cases} Rightarrow begin{cases} a-b=3\ a+b=frac53 end{cases} Rightarrow \ Rightarrow begin{cases} 2a=3+frac53\ 2b=frac53-3 end{cases} Rightarrow begin{cases} a=frac73\ b=-frac23 end{cases} end{gather*} Находим угловой коэффициент и свободный член из любого из двух уравнений касательных: $$ k=2a-5=2cdotfrac73-5=-frac13, b=6-a^2=6-frac{49}{9}=frac59 $$ Уравнение общей касательной: $$ y=-frac x3+frac59 $$ 
Точки касания: begin{gather*} a=frac73, f_1(a)=left(frac73right)^2-5cdotfrac73+6=frac{49}{9}-frac{35}{3}+6=frac{49-105+54}{9}=-frac29\ b=-frac23, f_2(b)=left(-frac23right)^2-frac23+1=frac49-frac23+1frac{4-6+9}{9}=frac79 end{gather*}
Ответ: касательная (y=-frac x3+frac59); точки касания (left(frac73;-frac29right)) и (left(-frac23;frac79right))
Пример 5*. Докажите, что кривая (y=x^4+3x^2+2x) не пересекается с прямой (y=2x-1), и найдите расстояние между их ближайшими точками.
Решим уравнение: (x^4+3x^2+2x=2x-1) begin{gather*} x^4+3x^2+1=0Rightarrow D=3^2-4=5Rightarrow x^2=frac{-3pmsqrt{5}}{2} end{gather*} Оба корня отрицательные, а квадрат не может быть отрицательным числом.
Значит, (xinvarnothing) — решений нет, кривая и прямая не пересекаются.
Что и требовалось доказать.
Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом (k=2), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой (y=2x-1).
Строим уравнение касательной. По условию: (f'(x)=4x^3+6x+2=2) begin{gather*} 4x^3+6x=0Rightarrow 2x(2x^2+3)=0Rightarrow left[ begin{array}{l} x=0\ 2x^2+3=0 end{array} right. Rightarrow left[ begin{array}{l} x=0\ x^2=-frac32 end{array} right. Rightarrow left[ begin{array}{l} x=0\ xinvarnothing end{array} right. Rightarrow x=0 end{gather*} Точка касания (x_0=0, y_0=0^4+3cdot 0^2+2cdot 0=0).
Уравнение касательной: (y=2(x-0)+0=2x)
 |
Ищем расстояние между двумя параллельными прямыми: (y=2x) и (y=2x-1). Перпендикуляр из точки (0;0) на прямую (y=2x-1) имеет угловой коэффициент (k=-frac12), его уравнение: (y=-frac12 x+b). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и (b=0). |
Уравнение перпендикуляра: (y=-frac x2).
Находим точку пересечения прямой (y=2x-1) и перпендикуляра (y=-frac x2): begin{gather*} 2x-1=-frac x2Rightarrow 2,5x=1Rightarrow x=0,4; y=-frac{0,4}{2}=-0,2 end{gather*} Точка пересечения A(0,4;-0,2).
Находим расстояние (OA=sqrt{0,4^2+(-0,2)^2}=0,2sqrt{2^2+1^2}=frac{sqrt{5}}{5})
Ответ: (frac{sqrt{5}}{5})
7. Взаимосвязь функции и ее производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Значение производной в точке касания как тангенс угла наклона
Если к кривой (f(x)) проведена касательная в точке с абсциссой (x_0), то
[{large{color{royalblue}{f'(x_0)=mathrm{tg}, alpha, }}},]
где (alpha) – угол наклона касательной.
Значит, верна формула: (f'(x_0)=mathrm{tg}, alpha=k).
Заметим, что координаты точки (A) тогда можно записать как ( (x_0; f(x_0)) ) или ( (x_0; y_0) ),
где ( y_0=kx_0+b).
То есть ( y_0=f(x_0)).
Задание
1
#2090
Уровень задания: Равен ЕГЭ
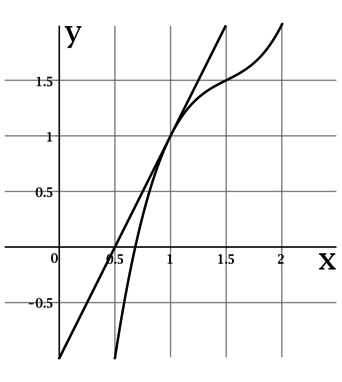
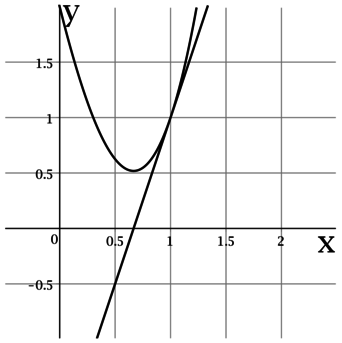
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))) (то есть угла между касательной к графику (f(x)) в точке ((x_0; f(x_0))) и положительным направлением оси (Ox)).
По рисунку видно, что касательная проходит через точки ((0,5; 0)) и ((1; 1)), тогда тангенс угла наклона касательной составляет (1 : 0,5
= 2), следовательно, (f'(x_0) = 2).
Ответ: 2
Задание
2
#2091
Уровень задания: Равен ЕГЭ
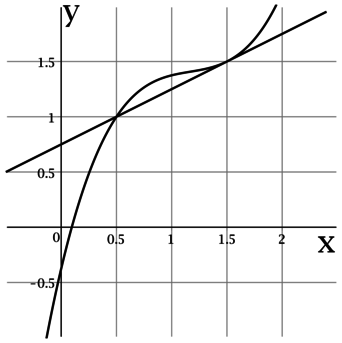
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
По рисунку видно, что касательная проходит через точки ((0,5; -0,5)) и ((1; 1)), тогда тангенс угла наклона касательной составляет (1,5 :
0,5 = 3), следовательно, (f'(x_0) = 3).
Ответ: 3
Задание
3
#2092
Уровень задания: Равен ЕГЭ
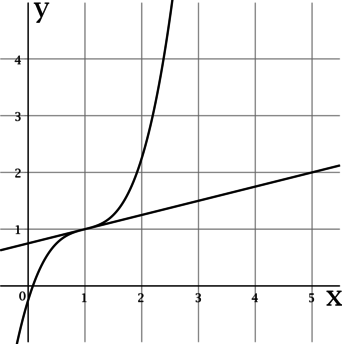
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
По рисунку видно, что касательная проходит через точки ((0,5; 1)) и ((1,5; 1,5)), тогда тангенс угла наклона касательной составляет (0,5
: 1 = 0,5), следовательно, (f'(x_0) = 0,5).
Ответ: 0,5
Задание
4
#2093
Уровень задания: Равен ЕГЭ
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
По рисунку видно, что касательная проходит через точки ((1; 1)) и ((5; 2)), тогда тангенс угла наклона касательной составляет ((2 — 1)
: (5 — 1) = 0,25), следовательно, (f'(x_0) = 0,25).
Ответ: 0,25
Задание
5
#3112
Уровень задания: Равен ЕГЭ
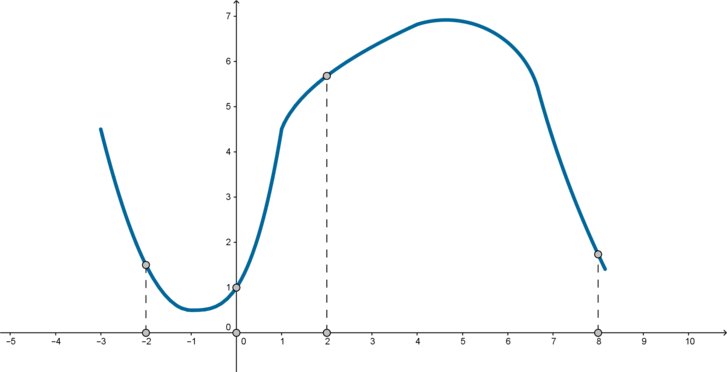
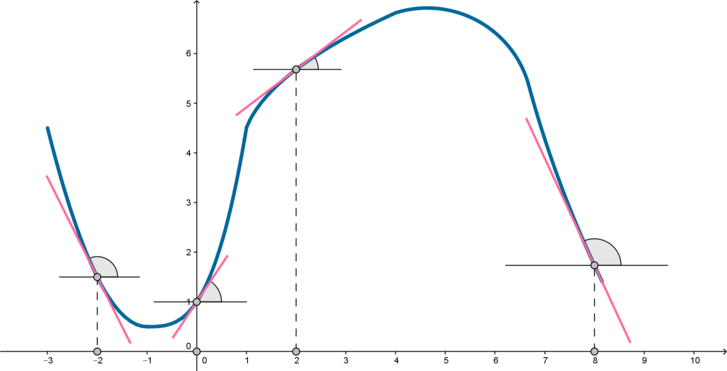
На рисунке изображен график функции (y=f(x)) и отмечены точки (-2;
0; 2; 
Проведем касательные к графику функции в этих точках. Так как тангенс угла (alpha) наклона касательной равен значению производной (f'(x)) в точке касания (x_0) ((f'(x_0)=mathrm{tg},alpha)), то нужно сравнить тангенсы углов, отмеченных на рисунке.
Вспомним, что если угол тупой, то его тангенс отрицательный, если острый – положительный. Следовательно, так как мы ищем наибольший тангенс, имеет смысл рассматривать только острые углы. Это углы, образованные касательными в точках (0) и (2). Заметим, что угол в точке (0) больше, следовательно, его тангенс также больше, чем тангенс угла в точке (2). Таким образом, ответ: (0).
Ответ: 0
Задание
6
#718
Уровень задания: Сложнее ЕГЭ
Производная (f'(x)) функции (f(x)) в точке (x_0) равна (10). Найдите котангенс угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
При всех (alpha), при которых (mathrm{tg}, alpha) и (mathrm{ctg}, alpha) имеют смысл, выполнено (mathrm{tg}, alphacdotmathrm{ctg}, alpha = 1), откуда котангенс угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))) равен (0,1).
Ответ: 0,1
Задание
7
#719
Уровень задания: Сложнее ЕГЭ
Производная (f'(x)) функции (f(x)) в точке (x_0) равна (5). Найдите сумму тангенса и котангенса угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
При всех (alpha), при которых (mathrm{tg}, alpha) и (mathrm{ctg}, alpha) имеют смысл, выполнено (mathrm{tg}, alphacdotmathrm{ctg}, alpha = 1), откуда котангенс угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))) равен (0,2), тогда сумма тангенса и котангенса угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))) равна (5,2).
Ответ: 5,2

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды