Как найти производную суммы нескольких функций - Avtoru.top

Нахождение
производной функции непосредственно
по определению часто связано с
определенными трудностями. На практике
функции дифференцируют с помощью ряда
правил и формул.

Пусть
функции u=u(х) и ν=ν(х) — две дифференцируемые
в некотором интервале (a;b) функции.

Теорема
20.2 .
Производная суммы (разности) двух функций
равна сумме (разности) производных этих
функций: (u±ν)’=u’±ν’.

Обозначим
у=u±ν. По определению производной и
основным теоремам о пределах получаем:

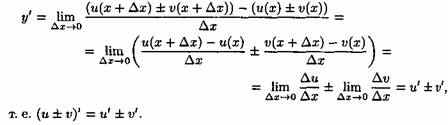
Теорема
справедлива для любого конечного числа
слагаемых.

Теорема
20.3 .
Производная произведения двух функций
равна произведению производной первого
сомножителя на второй плюс произведение
первого сомножителя на производную
второго: (u•ν)’=u’ν+v’u.

т.
е. (u•ν)’=u’•ν+u•ν‘.

При
доказательстве теоремы использовалась
теорема о связи непрерывности и
дифференцируемости: так как функции
u=u(х) и ν=ν(х) дифференцируемы, то они и
непрерывны, поэтому ∆ν→0 и ∆u→0 при
∆х→0.

Можно
показать, что:

а)
(с•u)’=с•u’, где с = const;

б)
(u•ν•w)’=u’v•w+u•v’•w+u•v•w’.

Теорема
20.4. Производная
частного двух функций
если
ν(х)≠0 равна дроби, числитель которой
есть разность произведений знаменателя
дроби на производную числителя и
числителя дроби на производную
знаменателя, а знаменатель есть квадрат
прежнего знаменателя:

Пусть
у=u/v. Тогда

Следствие
20.1.

Следствие
20.2.

20.5. Производная сложной и обратной функций

Пусть
у=ƒ(и) и u=φ(х), тогда у=ƒ(φ(х)) — сложная
функция с промежуточным аргументом u и
независимым аргументом х.

Теорема
20.5 .
Если функция u=φ(х) имеет производную
u’_х в
точке х, а функция у=ƒ(u) имеет производную
у’_u в
соответствующей точке u=φ(х), то сложная
функция у=ƒ(φ(х)) имеет производную у’_х в
точке х, которая находится по формуле
у’_х=у’_u-u’_х.

По
условию

Отсюда,
по теореме о связи функции, ее предела
и бесконечно малой функции, имеем

∆у=у’_u•∆u+α*∆u,
(20.6)

где
α→0 при ∆u→0.

Функция
u=φ(х) имеет производную в точке х:

этому

∆u=u¢_х •∆х+ß•∆х,
где ß→0 при ∆х→0.

Подставив
значение ∆u в равенство (20.6), получим

Δy=y¢_u(u’_х•∆х+ß*∆х)+а(u’_х•∆х+ß•∆х),

т.е.

∆у=у’u•u’_х•∆х+у’_u•ß•∆х+u’_х•а•∆х+α•ß•∆х.

Разделив
полученное равенство на ∆х и перейдя
к пределу при ∆х→О, получим у’_х=у’_u*u’_х.

Итак,
для нахождения производной сложной
функции надо производную данной функции
по промежуточному аргументу умножыть
на производную промежуточного аргумента
по независимому аргументу.

Это
правило остается в силе, если промежуточных
аргументов несколько. Так, если у=ƒ(u),
u=φ(ν), ν=g(х), то у’_х=у’_u•u’_ν•ν’_х.
Пусть у=ƒ(х) и х=φ(у) — взаимно обратные
функции.

Теорема
20.6 .
Если функция у=ƒ(х) строго монотонна на
интервале (a;b) и имеет неравную нулю
производную ƒ'(х) в произвольной точке
этого интервала, то обратная ей функция
х=φ(у) также имеет производную φ'(у) в
соответствующей точке, определяемую
равенством

Рассмотрим
обратную функцию х=φ(у). Дадим аргументу
у приращение ∆у¹ 0. Ему соответствует
приращение ∆х обратной функции, причем
∆х¹ 0 в силу строгой монотонности
функции у=ƒ(х). Поэтому можно записать

Если
∆у→0, то в силу непрерывности обратной
функции приращение ∆х→0. И так как

то
из (20.7) следуют равенства

Таким
образом, производная
обратной функции равна обратной величине
производной данной функции.

Правило
дифференцирования обратной функции
записывают так:

<<
Пример 20.3

Найти
производную функции у=log₂³tg
x⁴.

Решение:
Данная функция является сложной. Ее
можно представить в виде цепочки
«простых» функций: у=u³,
где u=Iog₂z,
где z=tgq, где q=х⁴.
По правилу дифференцирования сложной
функции (у’_х=y’_u•u’_z•z’_q•q’_x)
получаем:

<<
Пример 20.4

Пользуясь
правилом   дифференцирования
обратной функции, найти производную
у’_х для
функции

Решение:
Обратная функция х=у³+1
имеет производную х’_y =3у².

Следовательно,

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Правила вычисления производных

7 апреля 2011

Скачать все правила

Если следовать определению, то производная функции в точке — это предел отношения приращения функции Δy к приращению аргумента Δx:

Вроде бы все понятно. Но попробуйте посчитать по этой формуле, скажем, производную функции f(x) = x
² + (2x + 3) · e
^x · sin x. Если все делать по определению, то через пару страниц вычислений вы просто уснете. Поэтому существуют более простые и эффективные способы.

Для начала заметим, что из всего многообразия функций можно выделить так называемые элементарные функции. Это относительно простые выражения, производные которых давно вычислены и занесены в таблицу. Такие функции достаточно просто запомнить — вместе с их производными.

Производные элементарных функций

Элементарные функции — это все, что перечислено ниже. Производные этих функций надо знать наизусть. Тем более что заучить их совсем несложно — на то они и элементарные.

Итак, производные элементарных функций:

Название	Функция	Производная
Константа	f(x) = C, C ∈ R	0 (да-да, ноль!)
Степень с рациональным показателем	f(x) = x ⁿ	n · x ^{n − 1}
Синус	f(x) = sin x	cos x
Косинус	f(x) = cos x	− sin x (минус синус)
Тангенс	f(x) = tg x	1/cos² x
Котангенс	f(x) = ctg x	− 1/sin² x
Натуральный логарифм	f(x) = ln x	1/x
Произвольный логарифм	f(x) = log_a x	1/(x · ln a)
Показательная функция	f(x) = e ^x	e ^x (ничего не изменилось)

Если элементарную функцию умножить на произвольную постоянную, то производная новой функции тоже легко считается:

(C · f)’ = C · f ’.

В общем, константы можно выносить за знак производной. Например:

(2x
³)’ = 2 · (x
³)’ = 2 · 3x
² = 6x
².

Очевидно, элементарные функции можно складывать друг с другом, умножать, делить — и многое другое. Так появятся новые функции, уже не особо элементарные, но тоже дифференцируемые по определенным правилам. Эти правила рассмотрены ниже.

Производная суммы и разности

Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:

(f + g)’ = f ’ + g ’
(f − g)’ = f ’ − g ’

Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)’ = f ’ + g ’ + h ’.

Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g, и тогда останется лишь одна формула — производная суммы.

Задача. Найти производные функций: f(x) = x
² + sin x; g(x) = x
⁴ + 2x
² − 3.

Функция f(x) — это сумма двух элементарных функций, поэтому:

f ’(x) = (x
² + sin x)’ = (x
²)’ + (sin x)’ = 2x + cos x;

Аналогично рассуждаем для функции g(x). Только там уже три слагаемых (с точки зрения алгебры):

g ’(x) = (x
⁴ + 2x
² − 3)’ = (x
⁴ + 2x
² + (−3))’ = (x
⁴)’ + (2x
²)’ + (−3)’ = 4x
³ + 4x + 0 = 4x · (x
² + 1).

Ответ:
f ’(x) = 2x + cos x;
g ’(x) = 4x · (x
² + 1).

Производная произведения

Математика — наука логичная, поэтому многие считают, что если производная суммы равна сумме производных, то производная произведения strike«>равна произведению производных. А вот фиг вам! Производная произведения считается совсем по другой формуле. А именно:

(f · g) ’ = f ’ · g + f · g ’

Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.

Задача. Найти производные функций: f(x) = x
³ · cos x; g(x) = (x
² + 7x − 7) · e
^x.

Функция f(x) представляет собой произведение двух элементарных функций, поэтому все просто:

f ’(x) = (x
³ · cos x)’ = (x
³)’ · cos x + x
³ · (cos x)’ = 3x
² · cos x + x
³ · (− sin x) = x
² · (3cos x − x · sin x)

У функции g(x) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:

g ’(x) = ((x
² + 7x − 7) · e
^x)’ = (x
² + 7x − 7)’ · e
^x + (x
² + 7x − 7) · (e
^x)’ = (2x + 7) · e
^x + (x
² + 7x − 7) · e
^x = e
^x · (2x + 7 + x
² + 7x −7) = (x
² + 9x) · e
^x = x(x + 9) · e
^x.

Ответ:
f ’(x) = x
² · (3cos x − x · sin x);
g ’(x) = x(x + 9) · e
^x.

Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию. А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.

Производная частного

Если есть две функции f(x) и g(x), причем g(x) ≠ 0 на интересующем нас множестве, можно определить новую функцию h(x) = f(x)/g(x). Для такой функции тоже можно найти производную:

Неслабо, да? Откуда взялся минус? Почему g
²? А вот так! Это одна из самых сложных формул — без бутылки не разберешься. Поэтому лучше изучать ее на конкретных примерах.

Задача. Найти производные функций:

В числителе и знаменателе каждой дроби стоят элементарные функции, поэтому все, что нам нужно — это формула производной частного:

По традиции, разложим числитель на множители — это значительно упростит ответ:

Ответ:

Производная сложной функции

Сложная функция — это не обязательно формула длиной в полкилометра. Например, достаточно взять функцию f(x) = sin x и заменить переменную x, скажем, на x
² + ln x. Получится f(x) = sin (x
² + ln x) — это и есть сложная функция. У нее тоже есть производная, однако найти ее по правилам, рассмотренным выше, не получится.

Как быть? В таких случаях помогает замена переменной и формула производной сложной функции:

f ’(x) = f ’(t) · t ’, если x заменяется на t(x).

Как правило, с пониманием этой формулы дело обстоит еще более печально, чем с производной частного. Поэтому ее тоже лучше объяснить на конкретных примерах, с подробным описанием каждого шага.

Задача. Найти производные функций: f(x) = e
^{2x + 3}; g(x) = sin (x
² + ln x)

Заметим, что если в функции f(x) вместо выражения 2x + 3 будет просто x, то получится элементарная функция f(x) = e
^x. Поэтому делаем замену: пусть 2x + 3 = t, f(x) = f(t) = e
^t. Ищем производную сложной функции по формуле:

f ’(x) = f ’(t) · t ’ = (e
^t)’ · t ’ = e
^t · t ’

А теперь — внимание! Выполняем обратную замену: t = 2x + 3. Получим:

f ’(x) = e
^t · t ’ = e
^{2x + 3} · (2x + 3)’ = e
^{2x + 3} · 2 = 2 · e
^{2x + 3}

Теперь разберемся с функцией g(x). Очевидно, надо заменить x
² + ln x = t. Имеем:

g ’(x) = g ’(t) · t ’ = (sin t)’ · t ’ = cos t · t ’

Обратная замена: t = x
² + ln x. Тогда:

g ’(x) = cos (x
² + ln x) · (x
² + ln x)’ = cos (x
² + ln x) · (2x + 1/x).

Вот и все! Как видно из последнего выражения, вся задача свелась к вычислению производной суммы.

Ответ:
f ’(x) = 2 · e
^{2x + 3};
g ’(x) = (2x + 1/x) · cos (x
² + ln x).

Очень часто на своих уроках вместо термина «производная» я использую слово «штрих». Например, штрих от суммы равен сумме штрихов. Так понятнее? Ну, вот и хорошо.

Таким образом, вычисление производной сводится к избавлению от этих самых штрихов по правилам, рассмотренным выше. В качестве последнего примера вернемся к производной степени с рациональным показателем:

(x
ⁿ)’ = n · x
^{n − 1}

Немногие знают, что в роли n вполне может выступать дробное число. Например, корень — это x
^0,5. А что, если под корнем будет стоять что-нибудь навороченное? Снова получится сложная функция — такие конструкции любят давать на контрольных работах и экзаменах.

Задача. Найти производную функции:

Для начала перепишем корень в виде степени с рациональным показателем:

f(x) = (x
² + 8x − 7)^0,5.

Теперь делаем замену: пусть x
² + 8x − 7 = t. Находим производную по формуле:

f ’(x) = f ’(t) · t ’ = (t
^0,5)’ · t ’ = 0,5 · t
^−0,5 · t ’.

Делаем обратную замену: t = x
² + 8x − 7. Имеем:

f ’(x) = 0,5 · (x
² + 8x − 7)^−0,5 · (x
² + 8x − 7)’ = 0,5 · (2x + · (x
² + 8x − 7)^−0,5.

Наконец, возвращаемся к корням:

Ответ:

Смотрите также:

Вводный урок по вычислению производных степенной функции
Уравнение касательной к графику функции
Тест к параграфу «Что такое логарифм» (легкий)
Комбинаторика в задаче B6: легкий тест
Задача B2: лекарство и таблетки
Задача B4 про шерсть и свитер

Источник

Алгебра и начала математического анализа, 11 класс

Урок №11. Правила дифференцирования.

Перечень вопросов, рассматриваемых в теме:

разбор основных правил дифференцирования функций;
примеры вычисления производной линейной функции;
правила вычисления производных произведения и частного.

Глоссарий по теме

Производная суммы равна сумме производных.

Производная суммы нескольких функции равна сумме производных этих функции.

Производная разности равна разности производных.

Производная произведения равна произведению первого множителя на второй плюс первый множитель, умноженный на производную второго.

Производная частного равна производной числителя умноженного на знаменатель минус числитель умноженный на производную знаменателя и все это деленное на квадрат знаменателя.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

При вычислении производной используются следующие правила дифференцирования. Правило дифференцирования суммы двух функций.

Производная суммы равна сумме производных: (f(x) + g(x))’ = f ‘(x) + g'(x).

Подробно это свойство производной формулируется так: Если каждая из функции f(x) и g(x) имеет производную, то их сумма также имеет производную и справедлива формула.

Производная суммы нескольких функции равна сумме производных этих функции:

(f(x) +…+ g(x))’ = f ‘(x) +…+ g'(x).

Производная разности равна разности производных: (f(x) — g(x))’ = f ‘(x) — g'(x).

А теперь рассмотрим пример применения данного правила дифференцирования.

Рассмотрим второе правило дифференцирования:

Постоянный множитель можно вынести за знак производной:

(cf(x))’=cf ‘ (x)

Переходим к третьему правилу дифференцирования. Производная произведения равна произведению первого множителя на второй плюс первый множитель, умноженный на производную второго. (f(x)·g(x)) ‘=f’ (x)·g(x)+f(x)·g’ (x)

Четвертое правило дифференцирования: производная частного равна производной числителя умноженного на знаменатель минус числитель умноженный на производную знаменателя и все это деленное на квадрат знаменателя.

Сложная функция

Производная сложной функции находится по формуле:

(f(g(x))) ‘=f ‘(g(x))·g’ (x)

Примеры и разборы решения заданий тренировочного модуля

Пример 1.

Найдем производную функции:

Решение:

производная суммы равна сумме производных. Найдем производную каждого слагаемого

Ответ:

Пример 2.

Найти производную функции f(x)=8x³+3x²-x.

Решение:

f(x)=8x³+3x²-x

f’(x)=(8x³)’+(3x²)’-x’

Рассмотрим каждый член многочлена по отдельности

(8x³) ‘=8(x³) ‘=8·3x²=24x²

(3x²) ‘=3(x²) ‘=3·x=6x

(-x) ‘=-(x) = -1

f’ (x)=(8x³) ‘+(3x²) ‘-x’=24x²+6x-1.

Ответ: f’ (x)=24x²+6x-1.

Пример 3.

Найти производную функции f(x)=(3x-4)(4-5x).

Решение:

Воспользуемся формулой производной произведения:

f’ (x)=(3х-4) ‘ (4-5х) + (3х-4)(4-5х) ‘=3(4-5х)-5(3х-4)=12-15х-15х+20= 32

Ответ: f’ (x)=32

Пример 4.

Найти производную функции

Решение:

Воспользуемся формулой производной частного:

Ответ:

Пример 5.

Найти производную функции F(x)=(2x-1)²

Решение:

По правилу нахождения производной от сложной функции, получаем:

F’ (x)=((2x-1)²) ‘·(2x-1)=2(2x-1)·2=4(2x-1)=8x-4.

Ответ: F’ (x)=8x-4.

Источник

Содержание:

Формула
Примеры вычисления производной суммы функций

Формула

$$(u(x)+v(x))^{prime}=u^{prime}(x)+v^{prime}(x)$$

Производная суммы равна сумме производных.

Примеры вычисления производной суммы функций

Пример

Задание. Найти производную функции $y(x)=3x+2$

Решение. Производная суммы равна сумме производных, тогда

$$y^{prime}(x)=(3 x+2)^{prime}=(3 x)^{prime}+(2)^{prime}$$

В первом слагаемом из под знака производной выносим тройку, а производная
второго слагаемого равна нулю, как производная константы. Тогда будем иметь

$$y^{prime}(x)=3 cdot(x)^{prime}+0=3 cdot 1=3$$

Ответ. $y^{prime}(x)=3=3$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Вычислить производную функции $y(x)=sin x+cos x$

Решение. Искомая производная

$$y^{prime}(x)=(sin x+cos x)^{prime}$$

Производная суммы равна сумме производных, тогда получаем:

$$y^{prime}(x)=(sin x)^{prime}+(cos x)^{prime}=cos x+(-sin x)=cos x-sin x$$

Ответ. $y^{prime}(x)=cos x-sin x$

Читать дальше: производная разности (u-v)’.

Источник

Лекция
3. Производная суммы, разности, произведения и
частного функций

Производные
основных элементарных функций.

План

1. Производная
степенной функции.

2. Правила дифференцирования. Производная сложной функции.

3. Производные
основных элементарных функций.

4. Таблица
производных

5. Решение задач.

(Учебник: Ш.А.
Алимов Алгебра и начала математического анализа 10-11 класс глава VIII §45, §46, §47, стр. 236-238, стр. 240-242, стр. 245-249)

1. Производная
степенной функции.

Итак, на предыдущих
занятиях нами были получены следующие формулы производных:

Четыре последние
формулы являются формулами производной степенной функции для . Их можно записать так:

Вообще, справедлива
формула производной степенной функции для любого действительного показателя:

. (1)

Эта формула
применима при тех значениях x, при которых её правая часть
имеет смысл.

Например, .

Пример 1

Вычислить , если .

Решение

Ответ:

Пользуясь формулами
и , можно найти производные степенной и линейной функций, например .

В более сложных
случаях, например при нахождении производной функции , можно воспользоваться следующей формулой: . (2)

По формуле (2) при k = 3, b = -1, p = 7 имеем .

2. Правила дифференцирования. Производная сложной функции.

При вычислении
производной используются следующие правила дифференцирования суммы,
произведения и частного:

1. Производная суммы равна сумме производных:

(3)

Подробно это
свойство производной формулируется так: если каждая из функций и имеет производную, то их сумма также имеет производную и справедлива
формула (3).

Производная суммы
нескольких функций равна сумме производных этих функций, производная разности
равна разности производных.

Пример 2

Найдите производную
функции:

1) ; 2) .

Решение

1) ;

2) .

Ответ: 1) ; 2) .

2. Постоянный множитель можно вынести за знак производной:

(4)

Пример 3

Вычислить .

Решение

Ответ: -9

3. Производная
произведения:

(5)

Пример 3

Найдите производную функции , если .

Решение

По формуле (5) находим .

Ответ:

4. Производная
частного:

(6)

Формулы (5) и (6)
справедливы при условии, что функции и имеют производную в точке x, причём в раенстве (6)
.

Пример 4

Найдите производную
функции .

Решение

Обозначим . По формуле (6) находим .

Ответ:

Производная сложной функции.

Рассмотрим функция . Эту функцию можно рассматривать как сложную функцию , где , т.е. как функцию , аргумент которой также является функцией . Иными словами, сложная функция – это функция от функции . Производная сложной функции находится по формуле , где , т.е. по формуле

. (7)

Рассмотрим примеры.

1) Пусть .

Здесь .

По формуле (7)
находим .

2) Пусть . Здесь . По формуле (7) находим
.

3. Производные
основных элементарных функций.

Элементарными
функциями нвзывают степенную, показательную,
логарифмическую и тригонометрические функции, а также из различные комбинации.
При решении многих практических задач часто приходится находить производные
таких функций.

Например,
напряжение в цепи переменного тока выражается формулой ; для нахождения силы тока нужно уметь находить производную , так как .

1) Производная
показательной функции.

Показательная
функция , где , определена на всей числовой прямой и имеет производную в каждой её
точке. Любую показательную функцию можно выразить через показательную функцию с
основанием e по формуле , (8)

так как . В курсе высшей математики доказывается, что функция обладает замечательным свойством: её производная также равна , т.е.

(9)

Применяя правило
дифференцирования сложной функции, получаем

(10)

Например, .

Пример 5

Найдите производную
функции , где .

Решение

Используя формулы
(8) и (10), находим .

Итак, (11)

Ответ:

Например, .

2) Производная
логарифмической функции.

Логарифмическую
функцию с любым основанием можно выразить через логарифмическую функцию с основанием e
с помощью формулы перехода

. (12)

Производная функции
выражается формулой . (13)

Применяя правило дифференцирования
сложной функции, получаем

. (14)

Например, .

Пример 6

Найти производную
функции , где .

Решение

Используя формулы
(12) и (13), находим

Итак, . (15)

Ответ:

3) Производные
тригонометрических функций.

Справедливы
следующие формулы:

; . (16)

Применяя правило
дифференцирования сложной функции, имеем следующие формулы

Например, ,

Пример 7

Найдите производную
функции .

Решение

Используя правило
дифференцирования частного и формулы (16), находим

Итак, . (17)

Ответ:

Пример 8

Найдите производную
функции:

1) ;

2) ;

3) .

Решение

1) ;

2) ;

3) .

Пример 9

Найдите значение x, при которых значение производной функции равно нулю; положительно; отрицательно.

Решение

Найдем производную .

Заметим, что
равенство справедливо при тех значениях x, при которых обе
части имеют смысл, т.е. при .

Выражение равно нулю при , положительно на промежутках
; отрицательно на промежутках .

Так как , то только при ; при ; при
.

Ответ: при ; при ; при .

5. Задания для самостоятельного решения.

Задача 1

Вычислите
производную при данном значении аргумента x:

Задача 2

Вычислите
производную при данном значении аргумента x:

Задача 3

Найдите , если: .

Задача 4

Вычислите
производную при данном значении аргумента x: .

Задача 5

Найдите производную
функции .

В ответе укажите
номер правильного ответа.

1. 2. 3. 4.

Задача 6

Найдите , если .

Задача 7

Найти значение
производной функции в точке :

Задача 8

Выяснить, при каких
значениях x значение производной функции
равно нулю (.

Если у вас
получилось больше одного значения, перечислите их через точку с запятой (;) без
пробелов в порядке возрастания.

Задача 9

Найдите значение
производной функции в точке .

Задача 10

Найдите значение
производной функции в точке .

Источник

20.5. Производная сложной и обратной функций

Правила вычисления производных

Производные элементарных функций

Производная суммы и разности

Производная произведения

Производная частного

Производная сложной функции

Формула

Примеры вычисления производной суммы функций

Не пропустите также: