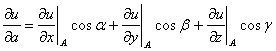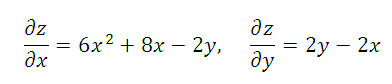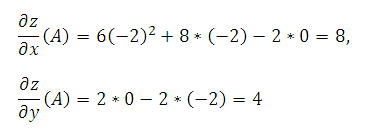Как найти производную по направлению онлайн калькулятор - Avtoru.top

Градиент функции

Градиент — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины u. Другими словами, направление градиента есть направление наибыстрейшего возрастания функции.

Назначение сервиса. Онлайн калькулятор используется для нахождения градиента функции нескольких переменных. (см. пример) При этом решаются следующие задачи:

нахождение частных производных функции, запись формулы градиента, вычисление наибольшой скорости возрастания функции в указанной точке;
вычисление градиента в точке A, нахождение производной в точке A по направлению вектора a;
нахождение полного дифференциала функции.

Шаг №1
Шаг №2
Видеоинструкция
Оформление Word

Решение со всеми исходными формулами сохраняется в формате Word.

Полный дифференциал для функции двух переменных: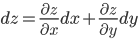

Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=d_xf(x,y,z)dx+d_yf(x,y,z)dy+d_zf(x,y,z)dz

Алгоритм нахождения градиента

Вычисление частных производных по формуле:
Вычисление частных производных в точке A.
Нахождение направляющих углов вектора a.
Вычисление производной в точке A по направлению вектора a по формуле;
Наибольшая скорость возрастания функции в указанной точке равна модулю градиента функции в этой точке.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Источник

Формула производной по направлению

а) Дана функция z=z(x,y) , направляющий вектор l и точка А. Найти производную по направлению в точке.

Решение.Формула производной по направлению:

1) Находим частные производные:

2) Находим значение частных производных в точке A(-2; 0):

Частные производные можно найти с помощью калькулятора частные производные.

3) Находим направляющие косинусы:

Направляющие косинусы, т.е. координаты нормированного (единичного) вектора можно найти с помощью калькулятора нормировки вектора.

4) Полученные значения частных производных и направляющих косинусов подставляем в формулу производной по направлению, получаем:

Следующий пример.

б) Дана функция z=z(x,y) , точка А и точка N.

Найти производную в точке A по направлению точки N.

Решение. Выполнение первых двух пунктов решения совпадает с примером 1, поэтому начинаем с пункта 3.

3) Находим координаты направляющего вектора l:

4) Находим направляющие косинусы:

5) Полученные значения частных производных и направляющих косинусов подставляем в формулу производной по направлению, получаем:

Второй способ найти производную функции по направлению см. градиент функции.

Источник

Калькулятор для нахождения производной функции в точке по направлению вектора.

Найдите производную функции `z=x^2y+ln(xy)`в точке `M(1;1)` по направлению вектора `vecl=(4;3)`

Пример ввода функции:

`z=x^2y+ln(xy)` `M(1;1)` `vecl=(4;3)` -> `z`=x**2y+ln(xy) ->`M_x`=1 ->`M_y`=1 ->`vecl_x`=4 ->`vecl_y`=3

`z=x^3y+ln(x^3y)` `M(-1;-2)` `vecl=(-3;4)` -> `z`=x**3*y+ln(x**3*y) ->`M_x`=-1 ->`M_y`=-2 ->`vecl_x`=-3 ->`vecl_y`=4

`z=xy^3+ln(xy^3)` `M(1;1)` `vecl=(-3;-4)` -> `z`=x*y**3+ln(x*y**3) ->`M_x`=1 ->`M_y`=1 ->`vecl_x`=-3 ->`vecl_y`=-4

`z=x^2y+ln(x^2y^3)` `M(1;1)` `vecl=(-3;4)` -> `z`=x**2*y+ln(x**2*y**3) ->`M_x`=1 ->`M_y`=1 ->`vecl_x`=-3 ->`vecl_y`=4

`z=xy^2+ln(x+y)` `M(2;-1)` `vecl=(-3;4)` -> `z`=x*y**2+ln(x+y) ->`M_x`=2 ->`M_y`=-1 ->`vecl_x`=-3 ->`vecl_y`=4

Для решения задач необходима регистрация

Источник

Пусть функция задана в виде параметрических уравнений (т.н. параметрическое задание функции):

причем

где
x(t),
y(t)
— дифференцируемые функции и
x‘(t)≠0.
Тогда производная
dydx

определяется по формуле:

, причем

где

— производная от параметрического уравнения
y(t)
по параметру t и

— производная от параметрического уравнения
x(t),
по параметру t.

Наш онлайн сервис найдет производную от параметрической функции с подробным решением. Пример подробного решения, выдаваемого нашим сервисом, можно посмотреть
здесь.

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

производное:от:f(x)=3-4x^2,:x=5
производное:от:f(x)=4^xln(x),:x=4
производное:от:f(x)=4sin(x)+2x^{x},:x=2
производное:от:f(x)=ln(x),:x=17
Показать больше

Описание

Найти производную функции в заданной точке

derivative-point-calculator

Блог-сообщения, имеющие отношение к Symbolab

Advanced Math Solutions – Derivative Calculator, Implicit Differentiation

We’ve covered methods and rules to differentiate functions of the form y=f(x), where y is explicitly defined as…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Градиент функции

Алгоритм нахождения градиента

Формула производной по направлению

Калькулятор для нахождения производной функции в точке по направлению вектора.

Найдите производную функции `z=x^2y+ln(xy)`в точке `M(1;1)` по направлению вектора `vecl=(4;3)`

Пример ввода функции:

`z=x^2y+ln(xy)` `M(1;1)` `vecl=(4;3)` -> `z`=x**2*y+ln(x*y) ->`M_x`=1 ->`M_y`=1 ->`vecl_x`=4 ->`vecl_y`=3

`z=x^3y+ln(x^3y)` `M(-1;-2)` `vecl=(-3;4)` -> `z`=x**3*y+ln(x**3*y) ->`M_x`=-1 ->`M_y`=-2 ->`vecl_x`=-3 ->`vecl_y`=4

`z=xy^3+ln(xy^3)` `M(1;1)` `vecl=(-3;-4)` -> `z`=x*y**3+ln(x*y**3) ->`M_x`=1 ->`M_y`=1 ->`vecl_x`=-3 ->`vecl_y`=-4

`z=x^2y+ln(x^2y^3)` `M(1;1)` `vecl=(-3;4)` -> `z`=x**2*y+ln(x**2*y**3) ->`M_x`=1 ->`M_y`=1 ->`vecl_x`=-3 ->`vecl_y`=4

`z=xy^2+ln(x+y)` `M(2;-1)` `vecl=(-3;4)` -> `z`=x*y**2+ln(x+y) ->`M_x`=2 ->`M_y`=-1 ->`vecl_x`=-3 ->`vecl_y`=4

Для решения задач необходима регистрация

Номер Строки

Не пропустите также:

`z=x^2y+ln(xy)` `M(1;1)` `vecl=(4;3)` -> `z`=x**2y+ln(xy) ->`M_x`=1 ->`M_y`=1 ->`vecl_x`=4 ->`vecl_y`=3