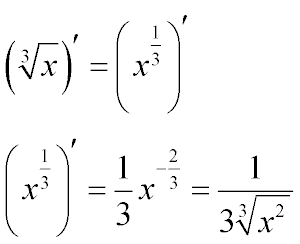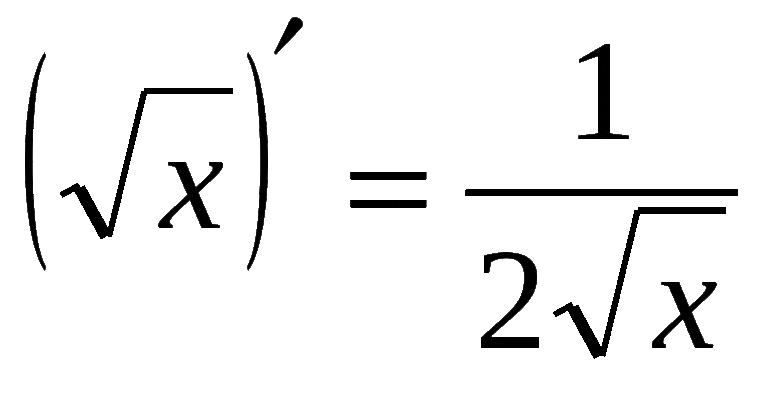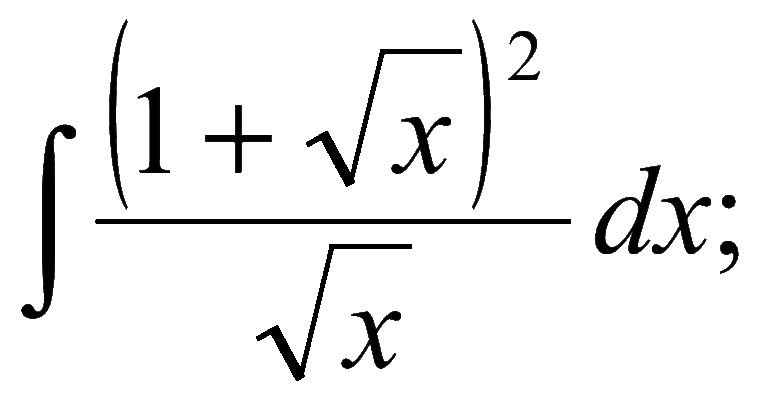Как найти производную корня в знаменателе

Сообщения без ответов | Активные темы

Автор	Сообщение
	Заголовок сообщения: Найти производную дроби с квадратным корнем в знаменателе Добавлено: 24 июн 2011, 12:05
Начинающий Зарегистрирован: 29 май 2011, 16:39 Сообщений: 43 Cпасибо сказано: 20 Спасибо получено: 0 раз в 0 сообщении Очков репутации: 1	Возникла проблема-не могу справиться с этой бякой — не получается найти производную дроби с квадратным корнем в знаменателе: [math]y=frac{x^2}{2sqrt{1-x^2}}[/math] по формуле разложил,а дальше вот никак [math]f(y)’= frac{(x^2)’ cdot 2sqrt{1-x^2}-x^2 cdot (2sqrt{1-x^2})’}{left(2sqrt{1-x^2}right)’}[/math] Помогите, пожалуйста, с решением
Вернуться к началу

kumana	Заголовок сообщения: Re: производная Добавлено: 27 июн 2011, 21:14
	[math]y’=frac{x(2-x^2)}{2sqrt{(1-x^2)^3}[/math]
Вернуться к началу

AarAir	Заголовок сообщения: Re: Найти производную дроби с квадратным корнем в знаменателе Добавлено: 27 мар 2013, 23:22
	[math]y = frac{x^{2}}{2sqrt{1-x^{2}}}[/math] [math]y’ = frac{(x^{2})’2sqrt{1-x^{2}- x^{2}(2sqrt{1-x^{2}})’}}{4sqrt{1-^x{2}}^{2}}[/math] [math]y’ = frac{2xsqrt{1-x^{2}}- frac{2x^{2}(-2x)}{2sqrt{1-x^{2}}}}{4sqrt{1-x^{2}}^{2}}[/math] [math]y’ = frac{2(x(1-x^{2}) + x^{3})}{4^sqrt{1-x^{2}}{3}}[/math] [math]y’ = frac{x}{2^sqrt{1-x^{2}}{3}}[/math]
Вернуться к началу

Была ли эта статья полезной?

См. также: 

таблица производных простых функций

таблица производных логарифмических функций

таблица производных тригонометрических функций

Производная корня. Формулы для нахождения производной корня

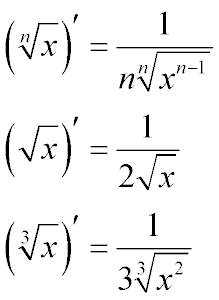
1. Общий случай формулы производной корня произвольной степени — дробь, в числителе которой единица, а в знаменателе число, равное степени корня, для которого вычислялась производная, умноженная на корень такой же степени, подкоренное выражение которого — переменная в степени корня, для которого вычислялась производная, уменьшенной на единицу
2. Производная квадратного корня — является частным случаем предыдущей формулы. Производная квадратного корня из x — это дробь, числитель которого равен единице, а знаменатель — двойка, умноженная на квадратный корень х
3. Производная кубического корня, также частный случай общей формулы. Производная кубического корня — это единица, деленная на три кубических корня из икс квадрат.

Ниже приведены преобразования, поясняющие, почему формулы нахождения производной квадратного и кубического корня именно такие, как приведены на рисунке. 

Разумеется, данные формулы можно вообще не запоминать, если принять во внимание, что извлечение корня производной степени — это то же самое, что возведение в степень дроби, знаменатель которой равен той же степени. Тогда нахождение производной корня сводится к применению формулы нахождения производной степени соответствующей дроби.

Производная переменной под квадратным корнем

( √x )’ = 1 / ( 2√x )   или 1/2 х^-1/2  

2080.1947
 

 Производная дроби |

Описание курса

| Нахождение экстремума функции 

Понятие производной

Смысл производной основан на понятии предела функции. Состоит запись выражения из трёх частей, в одной из которых указывается, к чему стремится неизвестное. Оно может достигать как нуля, так и бесконечности. Таким образом, предел представляет собой динамическую величину. Например, пусть имеется некая функция f (x) = (1 + x)^1/x.

При иксе, который равен нулю, функция будет не определена, но можно исследовать, как она будет себя вести при приближении переменной к нулю. Для этого можно взять какое-либо значение икса и, подставив его в уравнение, вычислить функцию. Затем в формулу подставить иное произвольное число, но такое, чтобы оно было меньше предыдущего, то есть приближалось к нулю.

Выполнив несколько таких вычислений, можно увидеть, что значение функции начнёт приближаться к некой величине. Это значение и считается пределом рассматриваемого выражения при иксе, стремящемся к нулю.

Следует рассмотреть другую функцию: f (x) = 1 / x. Подставляя вместо икса различные числа, можно будет отметить, что при уменьшении исходной величины переменной числовое значение в ответе увеличивается, то есть результат функции ничем не ограничивается. Это означает, что при иксе, который стремится к нулю, предел будет равняться бесконечности.

Понятие предела помогает дать определение непрерывности. Функция f (x) непрерывна в точке x = c только тогда, когда знак предела и выражения можно поменять друг с другом местами: lim f (x) = f (lim x) = f с. Используя это свойство, можно определить точки разрыва и непрерывность. Зная определения можно понять, что представляет собой производная.

Пусть имеется линейная функция y = k * x + b, графиком которой будет прямая. При изменении икса на дельту по игреку будет происходить прирост на Δy = k * Δx. Получается, что величина k является скоростью роста функции: k = (f (x + Δx) — f (x)) / Δx. В этом случае график прямой имеет постоянный наклон, поэтому коэффициент k — константа.

Если же функция имеет произвольный вид, например, она состоит из сложного многочлена с дробями и квадратами, то, как вычислить постоянную k, непонятно. Вот тут на помощь и приходит понятие производной. Можно взять отношение дельта-икс на дельта-игрек и посмотреть, какой предел будет у функции: f'(x) = lim (f (x + Δx) — f (x)) / Δx. По сути, это действие и является нахождением производной.

Свойства корня

Находить производные подкоренных выражений невозможно без знания свойств степеней и корней. По определению, корнем квадратным из произвольного числа, которое больше нуля, называется такое неотрицательное число, которое при возведении в квадрат равняется этому числу.

То есть выражение √a = b тождественно равенству: b² = a. Например, √16 = 4, так как 4² = 16. Таким образом, можно утверждать, что корнем энной степени числа а будет такое выражение, которое при возведении в эту степень будет равняться а. Степень корня указывается в верхнем регистре значка, а основание записывается под знаком корня и называется подкоренным выражением.

Выделяют следующие свойства корней:

1. Если подкоренное выражение представляет умножение неотрицательных чисел, то корень квадратный будет равняться произведению корней членов выражения: √ a * b * … * n = √ a * √ b * … * √ n.
2. Когда под корнем находится отношение двух положительных чисел, то для решения выражения нужно извлечь корень из числителя и знаменателя, а после выполнить деление: √ a / b = √ a / b = √ a / √ b.
3. В случае когда а больше или равняется нулю и при этом n является натуральным, то корень из подкоренного выражения будет равняться а в степени n: √ a²ⁿ = aⁿ.
4.  
5. При действительном числе и чётном значении показателей подкоренного выражения будет справедливым равенство: ^2*m√ a^2*m = | a |. Если же показатель нечётный, то в ответе действительное число будет всегда положительное.
6. При извлечении корня из корня ⁿ√ ^m√ действие можно заменить произведением показателей при неизменном подкоренном выражении.
7. Сложение и вычитание корней возможно только в том случае, когда количественные или буквенные значения подкоренных выражений совпадают: n √ m + k √ m = (n + k) √ m.
8. Умножить корни с одинаковыми показателями возможно лишь тогда, когда показатель у всех перемножаемых членов одинаков: √ n * √ m = √ n * m.

Для любой степени существует основная формула, по которой может быть найдена производная.

Выглядит она как (xⁿ)’ = n * x^{n -1}. Эта формула используется и для дифференцирования корней. Кроме этого, для успешного решения задач на нахождение производной квадратного корня из х необходимо знать и свойства степеней.

Нахождение выражения из Х

В общем случае формула производной корня из х равна дроби, в числителе которой стоит единица, а в знаменателе произведение степени корня на корень той же степени в подкоренном выражении, где находится неизвестное, уменьшенное на единицу, в степени. Математически это теорема записывается следующей формулой: (ⁿ√x)’ = 1 / (n * ⁿ√ x^n-1).

Эта формула имеет название первообразной. Она подходит для использования в выражениях любой кратности. В качестве примера можно рассмотреть взятие производной квадратного и кубического корня.

Так, для квадратного степенного уравнения справедливо выражение: (n√x)’ = 1 / 2 * √x. То есть производная квадратного корня х является дробью, делимое которой равняется единице, а делитель состоит из двойки, умножаемой на квадратный корень из неизвестного.

Аналогично можно сформулировать теорему и для нахождения производной кубического корня из x. Для этого случая решением задания на вычисление производной будет дробь, в числителе которой находится единица, а в знаменателе произведение тройки на корень кубический из икса в степени два. Формула для вычисления выглядит следующим образом: (³√x)’ = 1 / (3 ³ √x²).

Можно обратить внимание, что, по сути, операция сводится к таким же действиям, как и при возведении дробей в степень, когда делитель равняется тому же показателю.

Иными словами, вычисление производной коренного выражения сводится к использованию формул для нахождения функции дроби.

Для доказательства формул используют следующие рассуждения. Производная переменной под квадратным корнем это то же, что и нахождение функции при возведении многочлена в степень одна вторая: (√x)’ = (х ^½)’. Поэтому можно воспользоваться формулой для расчёта производной неизвестного числа в степени эн. А значит, запись вида (х^½)’ = ½ х^-½ = 1 / (2√х) будет верной.

Формула производной третьей степени доказывается по такому же принципу. Используя правило дифференцирования и переписав кубический корень как тройную степень, можно записать: (³√x)’ = (х ^1/3 )’ = 1 / 3 * (x-^2/3) = 1 / 3 * (³√х²). Тут следует отметить, что степень -2/3 образовывается путём вычитания единицы из дроби, в числителе которой стоит два, а в знаменателе три.

Примеры заданий

При взятии производной функции f (x) = ⁿ√х^m необходимо привести корень к степенному виду: f (x)’ = (ⁿ√х ^m)’ = x^m/n.

Так как из производных степени известно, что (x^m)’ = m * x^m-1, то и алгоритм решения для нахождения ответа коренного выражения сводится к преобразованию исходного уравнения путём перехода к степени: f (x)’ = (ⁿ√х^m)’ = (x^m/n)’ = m/n * x (^{m/n) -1} = (m/n * ⁿ√х^m-n).

Этот подход позволяет не запоминать сложную формулу, что часто и используется на практике.

Для закрепления теории следует решить несколько типовых примеров:

1. Определить, чему будет равна производная от корня квадратного, кратного разности три минус икс в квадрате. Запись условия задачи выглядит так: (√ 3 — x ²)’. Мысленно можно обозначить выражение в скобках буквой S. Получается, что задача будет состоять в поиске производной (√ S)’. Используя знание формулы, можно утверждать, что (√ S)’ = S’ / (2 * √ S). Ту же самую формулу можно будет получить, воспользовавшись преобразованием задания в степенную функцию: (√ S)’ = (S^½)^‘ = (½) * S^{(½ — 1 )} * S’ = S^-½ * S’ / 2 = S’ / (2 * √ S). Таким образом, (√ 3 — x ²)’ = (3 — x²)’ / (2 * √ 3 — x²) = — 2* x / 2 * √ 3 — x² = — x / √ 3 — x².
2. Рассчитать, чему будет равна производная функции 1 / (2 * 3√ x7). Исходное выражение нужно преобразовать так, чтобы неизвестная оказалась в числителе, а затем уже воспользоваться стандартным алгоритмом: (1 / 2 * 3√ x7)’ = 1 / 2 * (x-7/3)’. Теперь нужно взять производную от степенной функции. В итоге получится выражение: 1 / 2 * (-7 / 3) * x (-7/3) — 1 = -(7 / 6) * x-10/3 = (-7 / 6) * (1 / 3√ x10).
3. Необходимо найти производную суммы многочленов: p (x) = 3 + 4 √ x+3. По теореме дифференцирования ответ будет равняться сумме производных каждого члена равенства: p (x)’ = (3)’ + (4 √ x+3)’. Первое слагаемое равняется нулю, поэтому останется только найти производную корня. Используя снова правило производной, выражение можно переписать как 4 * (√ x+3)’. На следующем этапе многочлен в скобках нужно представить в виде степенной функции: (√x + 3)’ = 1 / ((2√x + 2)) * (x + 2)’ = 2 * (x +2)’ / √x+2. Так как производная суммы, это то же самое, что сумма производных, то будет верным записать: (4 √ x+2)’ = (2 / √x+2) *({(x)’ + (2)’}). Производная для двойки равна нулю, поэтому плюсовать её смысла нет. В итоге получится: p (x)’ = (3 + 4 √ x+3)’ = 2/ √x +2 = 2 / √x +2.

Расчёт на онлайн-калькуляторе

Попрактиковавшись в решении различных примеров, найти производную корня простых выражений будет довольно просто. Но если в заданиях будут стоять двойные корни или сама функция будет содержать большой многочлен, могут возникнуть проблемы. Связаны они обычно не с алгоритмом решения, а с трудностью вычисления и преобразования.

Такого рода задачи требуют повышенного внимания и скрупулёзности в расчётах. При этом поиску ответа понадобится уделить довольно много времени. Поэтому для помощи в нахождении производных коренных функций и существуют в интернете математические онлайн-калькуляторы.

Это сервисы, предлагающие бесплатно услуги по автоматическому расчёту производной любой сложности. Воспользоваться ими может каждый желающий, имеющий доступ к интернету. Для нахождения ответа не нужно обладать какими-то особыми знаниями. Всё что требуется от пользователя — ввести в предложенную форму условие и нажать кнопку «Вычислить». Весь процесс расчёта займёт одну-две секунды.

При этом большинство сервисов, кроме предоставления ответа на своих страницах, дает возможность ознакомиться с теоретическим материалом и предлагает рассмотреть решения заданий различной сложности. Поэтому вопроса, каким образом получился тот или иной ответ, возникнуть не должно.

Из различных онлайн-калькуляторов, считающих производные, можно выделить следующие:

1. Webmath.
2. Kontrolnaya-rabota
3. Onlinemschool.
4. Сalc.
5. Nauchniestati.

Сайты, используемые для вычислений, характеризуются интуитивно понятным интерфейсом, не содержащим нагромождения ненужной информации. На их страницах нет рекламного и вирусного кода.

Примечательно и то, что, выполнив пару вычислений, пользователь научится самостоятельно вычислять производную. А всё дело в том, что особенностью таких ресурсов является возможность обучения. Кроме непосредственно ответа, программа-расчётчик выдаст пошаговое вычисление с комментариями.

Кроме учащихся, онлайн-калькуляторы будут полезны и инженерам. Даже незначительная ошибка, допущенная в расчёте, приведёт к неверному ответу. В то же время при автоматических вычислениях появление ошибки исключено.