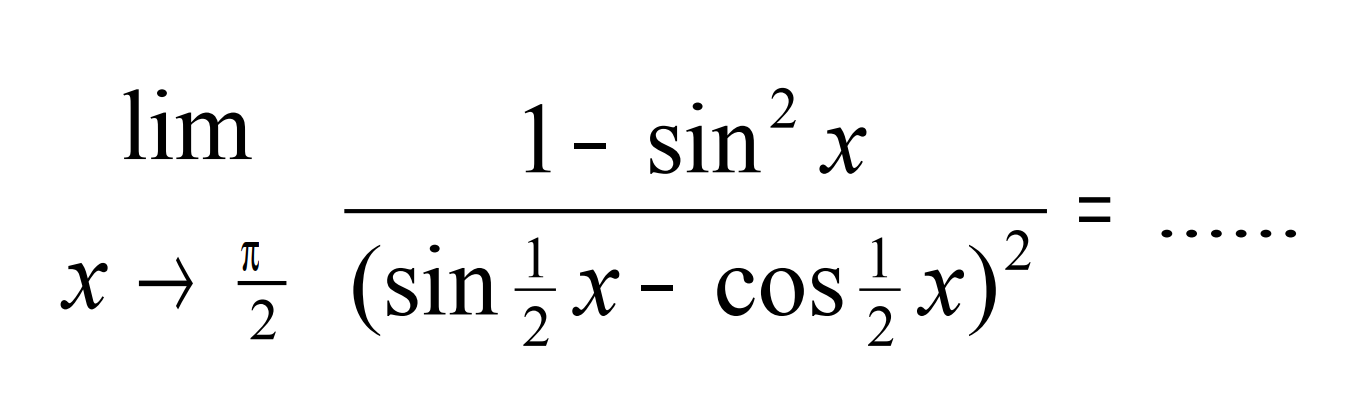Как найти производную cos в квадрате

Производная косинуса

Определение
По формуле производная косинуса равна отрицательному синусу: $$ (cos x)’ = -sin x $$

Если аргумент синуса является сложной функцией, тогда производная находится по формуле:

$$ (cos u(x))’ = -sin u(x) cdot ( u(x) )’ = -u'(x)sin u(x) $$

Пример 1
Найти производную косинуса двойного угла: $ y = cos 2x $
Решение

Аргумент косинуса представлен сложной функцией $ u(x) = 2x $. Поэтому применяем вторую формулу, в которой производная $ u'(x) = 2 $. Подставляем:

$$ y’ = (cos 2x)’ = -sin x cdot (2x)’ = -2sin x $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Ответ
$$ y’ = -2sin x $$
Пример 2
Чему равна производная косинуса в квадрате? $ y = cos^2 x $
Решение

В этом случае косинус представлен в виде степенной функции, производную которой можно найти по формуле: $ (x^p)’ = px^{p-1} $. Затем нужно выполнить домножение на производную самого косинуса. Выполняем:

$$ y’=(cos^2 x)’ = 2cos x cdot (cos x)’ = 2cos x cdot (-sin x) = -2 cos x sin x $$

По тригонометрической формуле синуса двойного угла: $ -2 cos x sin x = -sin 2x $

Записываем окончательный ответ:

$$ y'(x) = -2 cos x sin x = -sin 2x $$
Ответ
$$ y'(x) = -sin 2x $$
Пример 3
Найти производную косинуса в кубе функции $ y = cos^3 x $
Решение

Данный пример аналогичен предыдущему и решается по тем же формулам:

$$ y’ = (cos^3 x)’ = 3cos^2 x cdot (cos x)’ = $$

Так как $ (cos x)’ = -sin x $, то получаем:

$$ = 3cos^2 x cdot (-sin x) = -3cos^2 x sin x $$
Ответ
$$ y'(x) = -3cos^2 x sin x $$
Источник

Мэтуэй | Популярные задачи

1 Найти производную — d/dx бревно натуральное х
2 Оценить интеграл интеграл натурального логарифма x относительно x
3 Найти производную — d/dx
21 Оценить интеграл интеграл от 0 до 1 кубического корня из 1+7x относительно x
22 Найти производную — d/dx грех(2x)
23 Найти производную — d/dx
41 Оценить интеграл интеграл от cos(2x) относительно x
42 Найти производную — d/dx 1/(корень квадратный из х)
43 Оценка интеграла 9бесконечность
45 Найти производную — d/dx х/2
46 Найти производную — d/dx -cos(x)
47 Найти производную — d/dx грех(3x)
68 Оценить интеграл интеграл от sin(x) по x
69 Найти производную — d/dx угловой синус(х)
70 Оценить предел ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85 Найти производную — d/dx лог х
86 Найти производную — d/dx арктан(х)
87 Найти производную — d/dx бревно натуральное 5х92х равно произведению функции синуса и косинуса, то есть;

d/dx (cos 2 x) = — 2cos x sin x

Также найдите производную от cos

3 x, используя цепное правило и правило произведения.

Как вы доказываете дифференцирование cos квадрат x?

Существует множество способов получения производной от квадрата cos x. Следовательно, мы можем доказать производную от cos 2 x, используя;

  1. Цепное правило

  2. 92x производная по цепному правилу

    Чтобы доказать производную от квадрата cos по цепному правилу, предположим, что

    y = u 2 , где u = cos x

    По цепному правилу

    y = 2u. du/dx

    And,

    du/dx = -sin x

    Теперь, используя значение u и du/dx в y, мы имеем,

    y = — 2cos x.sin x

    Производная cos

    2 x с использованием правила произведения

    Правило произведения в производных используется, когда нам нужно вычислить производную двух функций одновременно. Правило продукта; 92 раза в течение нескольких секунд.

Часто задаваемые вопросы

Какие 3 производных правила?

Производные правила используются для простой оценки скорости изменения функции.

No related posts.

92)
9(3x) по отношению к x
92+1

Источник
Источник

См. также:

Таблица основных производных тригонометрических и обратных тригонометрических функций, синуса, косинуса, тангенса и котангенса, секанса и косенкансаДля нахождения производных от тригонометрических функций применяют следующие правила дифференцирования:

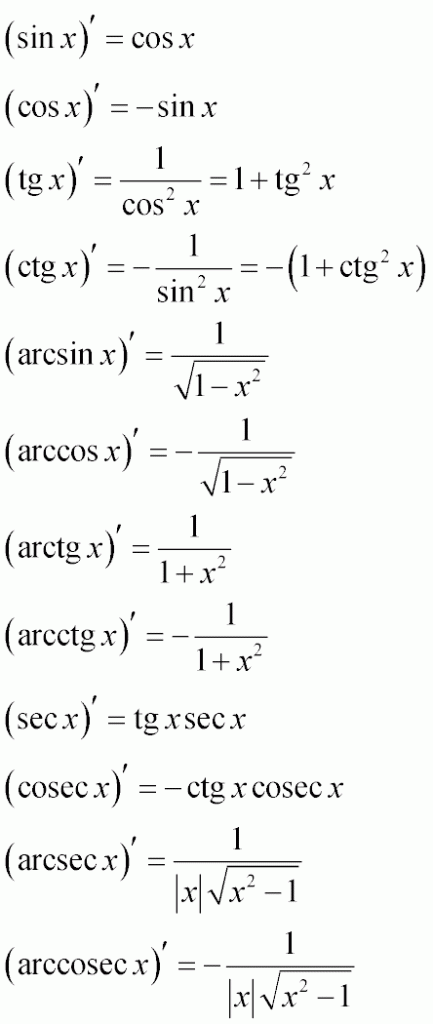
  1. (sin x )’ = cos x 

    Производная синуса от икс равна косинусу от икс
  2. (cos x )’ = -sin x 

    Производная косинуса от икс равна минус синус икс
  3. (tg x)’ = 1/ cos2x = 1 + tg2 x 

    Производную тангенса от икс можно найти как 

    • единицу, деленную на косинус квадрат икс
    • единицу плюс тангенс квадрат икс
  4. (ctg x)’ = — 1/ sin2x = -(1 + ctg2 x) 

    Производную котангенса от икс, аналогично можно представить двумя выражениями: 

    • минус единицу, деленную на синус квадрат икс
    • минус сумму единицы и котангенса квадрат икс
  5. (arcsin x)’ = 1/(√(1-x2))

    Производная арксинуса икс равна единице, деленной на корень из разности единицы и икс квадрат
  6. (arccos x)’ = -1/(√(1-x2))

    Производная арккосинуса икс равна минус единице, деленной на корень из разности единицы и икс квадрат
  7. ( arctg x )’ = 1 / ( 1 + x2 ) 

    Производная арктангенса от икс равна дроби, в числителе которой находится единица, а в знаменателе — единица плюс икс квадрат
  8. ( arcctg x )’ = -1 / ( 1 + x2 ) 

    Производная арккотангенса от икс равна минус единице, деленной на сумму единицы и икс квадрат
  9. (sex x)’ = tg x sec x

    Производная секанса от икс равна произведению тангенса икс и секанса икс
  10. (cosec x)’ = -ctg x cosec x

    Производная косеканса от икс равна минус котангенс икс умноженный на косеканс икс
  11. (arcsec x)’ = 1 / (|x|√(x2 -1))

    Производная арксеканса икс равна дроби, в числителе которой единица, а в знаменателе произведение модуля икс и корня квадратного разности икс квадрат и единицы
  12. (arccosec x)’ = — 1 / (|x|√(x2 -1)) 

    Производная арккосеканса икс равна дроби, в числителе которой минус единица, а в знаменателе произведение модуля икс и корня квадратного разности икс квадрат и единицы


2080.1947
 

 Таблица производных экспоненциальных и логарифмических функций |

Описание курса

| Производная числа 

Источник

Данный калькулятор вычисляет производную функции и затем упрощает ее.
В поле функция введите математическое выражение с переменной x, в выражении используйте стандартные операции + сложение, — вычитание, / деление, * умножение, ^ — возведение в степень, а также математические функции. Полный синтаксис смотрите ниже.
Упрощение полученной производной может занять некоторое время, для сложных функций — весьма продолжительное. Если ждать до конца нет сил — нажмите кнопку остановить. У меня получался достаточно простой вариант уже после 10-15 секунд работы алгоритма упрощения.

Калькулятор производных

PLANETCALC, Производная функции

Производная функции

Допустимые операции: + — / * ^
Константы: pi
Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch

Показать детали вычисления

Показать шаги вычисления производной и упрощения формулы

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Синтаксис описания формул

В описании функции допускается использование одной переменной (обозначается как x), скобок, числа пи (pi), экспоненты (e), математических операций: + — сложение, — — вычитание, * — умножение, / — деление, ^ — возведение в степень.
Допускаются также следующие функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec— экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, abs — абсолютное значение (модуль), sgn — сигнум (знак), logP — логарифм по основанию P, например log7(x) — логарифм по основанию 7, rootP — корень степени P, например root3(x) — кубический корень.

PLANETCALC, Таблица синтаксиса математических выражений

Таблица синтаксиса математических выражений

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Вычисление производной

Вычисление производной — дело нехитрое, достаточно знать несколько простых правил и формулы дифференцирования простых функций; сложнее в этом онлайн калькуляторе было сделать интерпретатор математических выражений и алгоритм упрощения полученного результата, но об этом как-нибудь в другой раз…

Правила дифференцирования

1) производная суммы:
(u+v+...+w)'=u'+v'+...+w'
2) производная произведения:
(uv)'=u'v+v'u
3) производная частного:
(frac{u}{v})'=frac{u'v-v'u}{v^2}
4) производная сложной функции равна произведению производных:
y=f(u), u=phi(x), y'=f'(u)phi'(x)

Таблица производных

Производная степенной функции:
(x^{n})'=nx^{n-1}
Производная показательной функции:
(a^{x})'=a^{x}ln(a)
Производная экспонециальной функции:
(e^{x})'=e^{x}
Производная логарифмической функции:
(ln(x))'=frac{1}{x}
Производные тригонометрических функций:
(sin{x})'=cos{x},
(cos(x))'=-sin(x),
(tan(x))'=frac{1}{cos^2(x)},
(cot(x))'=-frac{1}{sin^2(x)}
Производные обратных тригонометрических функций:
(arcsin(x))'=frac{1}{sqrt{1-x^2}},
(arccos(x))'=-frac{1}{sqrt{1-x^2}},
(arctg(x))'=frac{1}{1+x^2},
(arcctg(x))'=-frac{1}{1+x^2}
Производные гиперболических функций:
(sh(x))' = ch(x)
(ch(x))' = sh(x)
(th(x))' = -th(x)sech(x)
(cth(x))' = -csch^2(x)

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как составить заявление на отмену судебного приказа если закончился срок обжалования
  • Как найти угол в треугольнике используя стороны
  • Как найти нод разложением на простые множители
  • Как найти воду золотым кольцом
  • Как составить бизнес план парикмахерско

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии