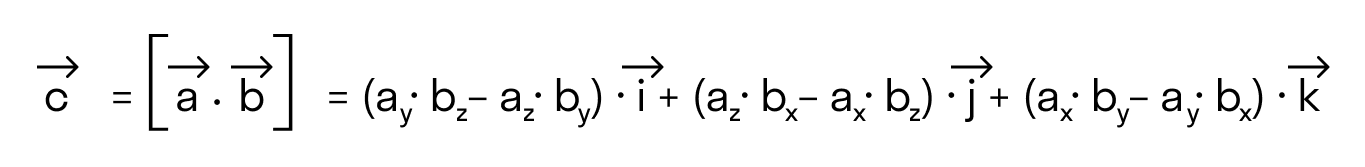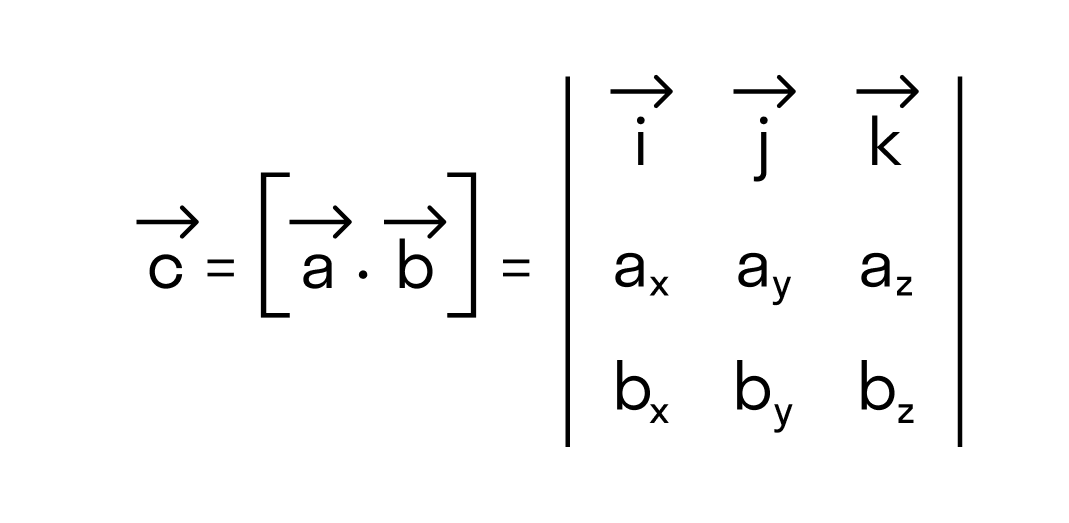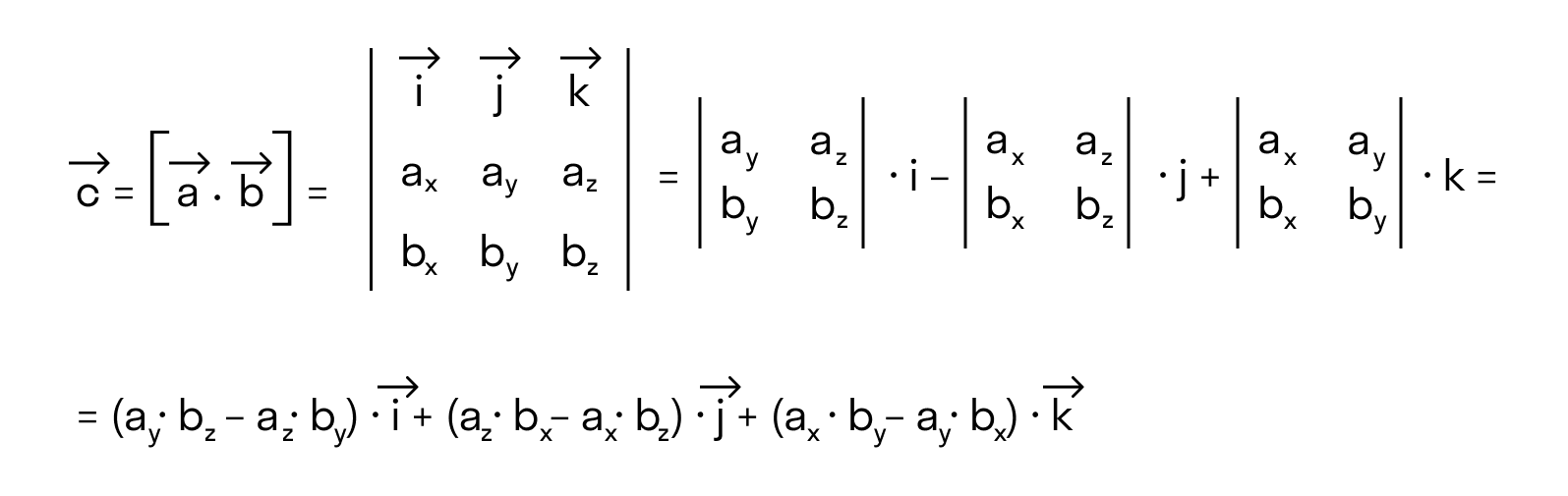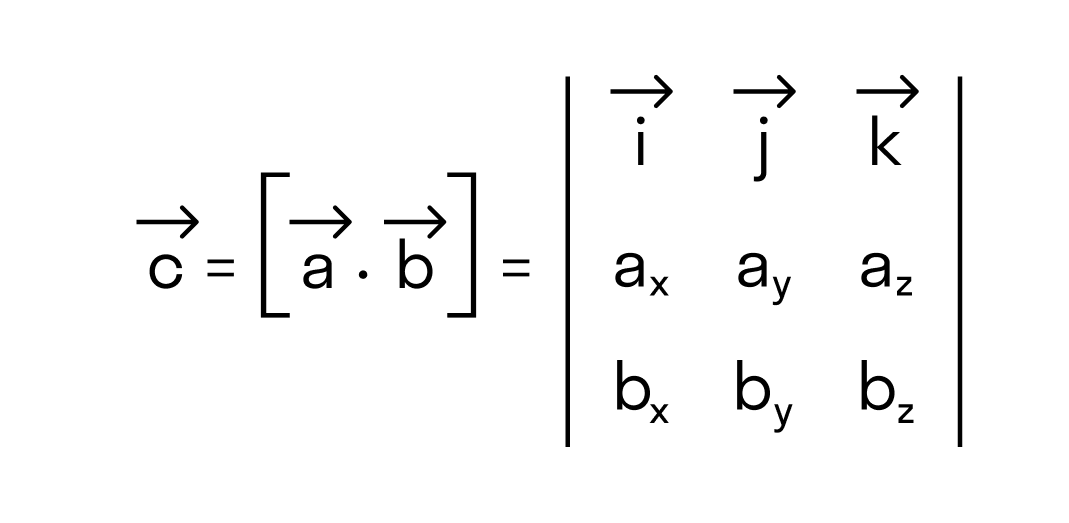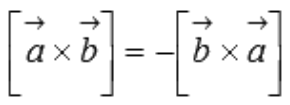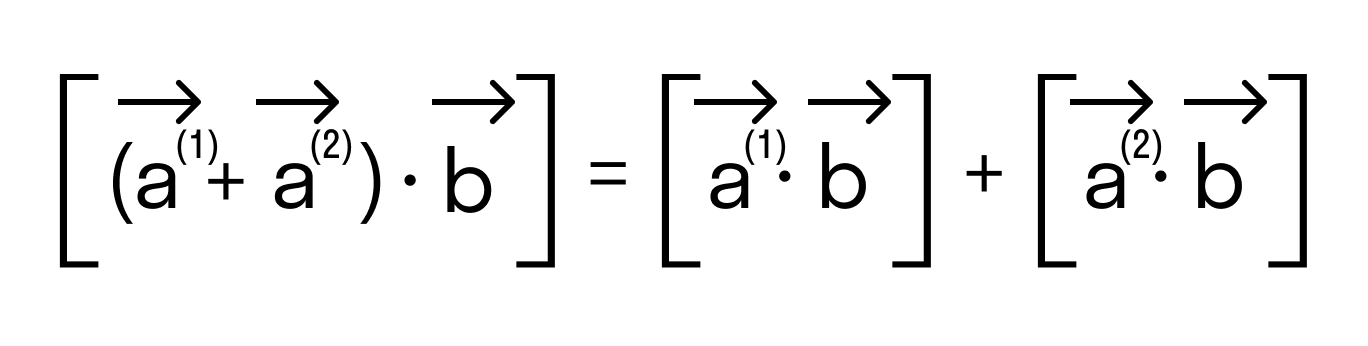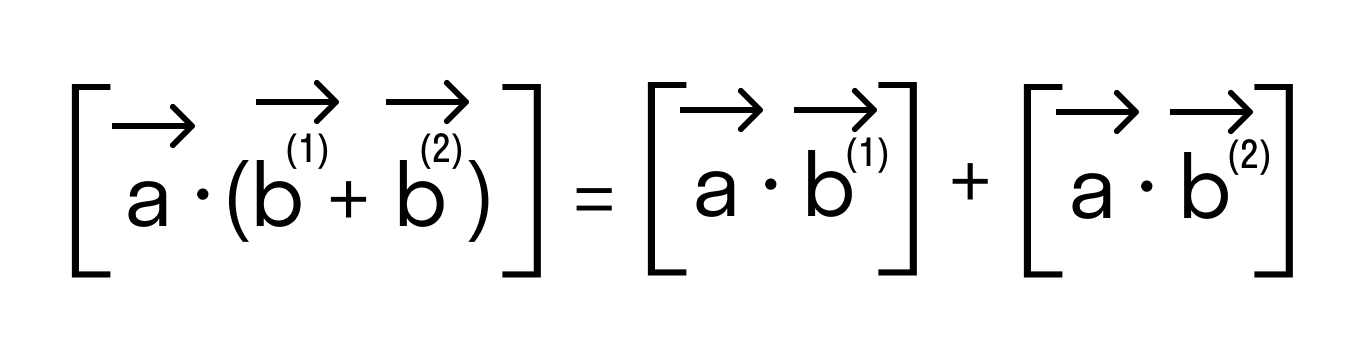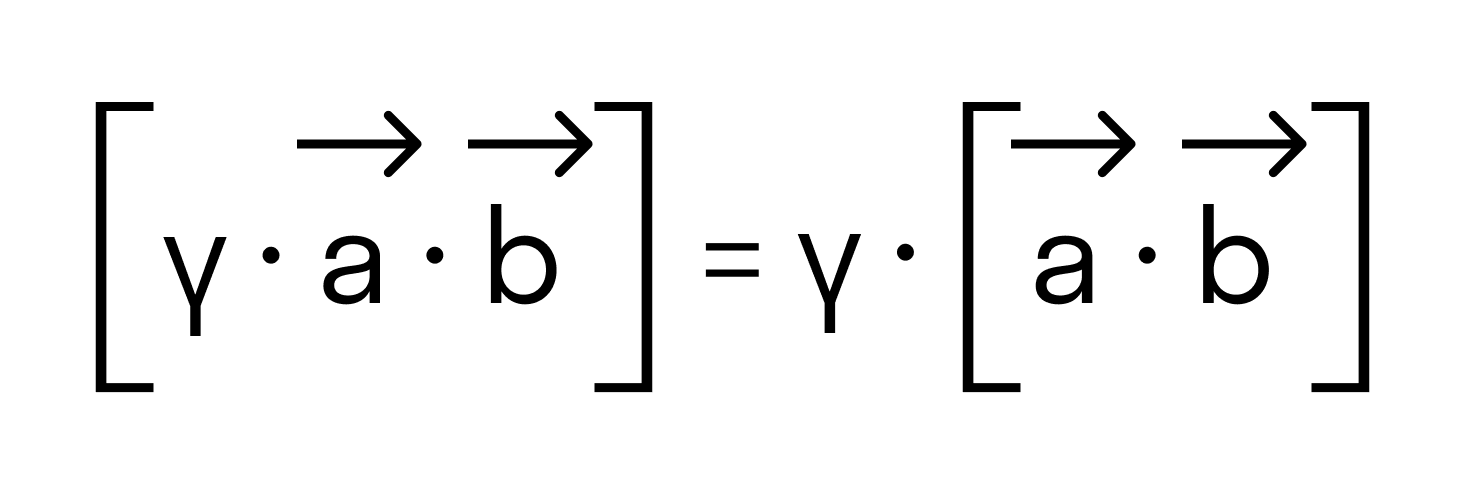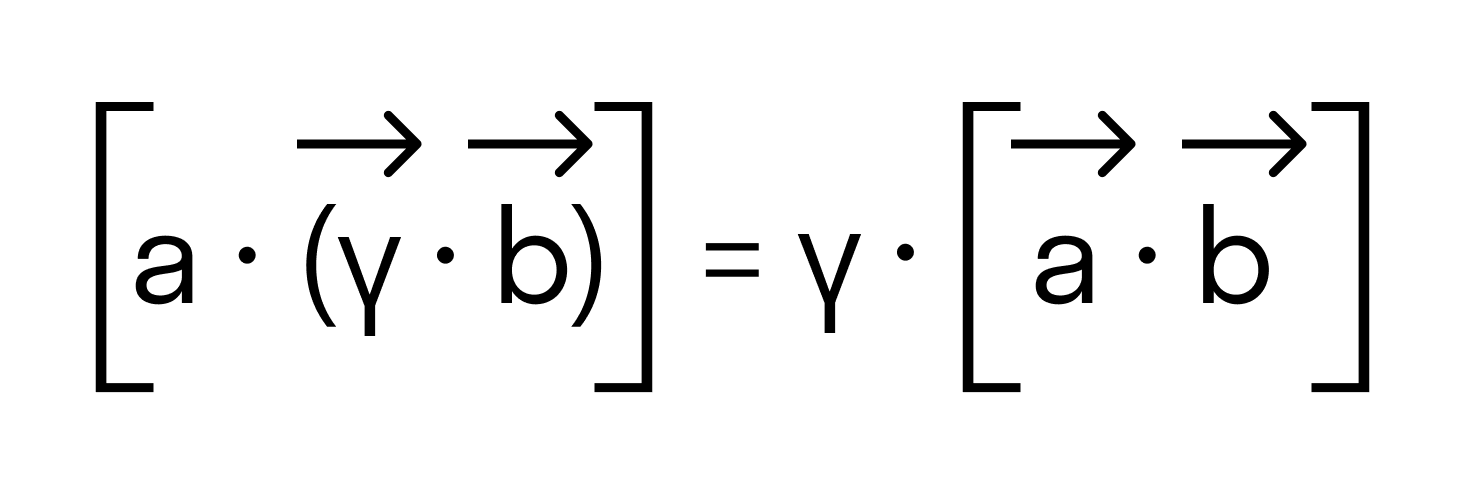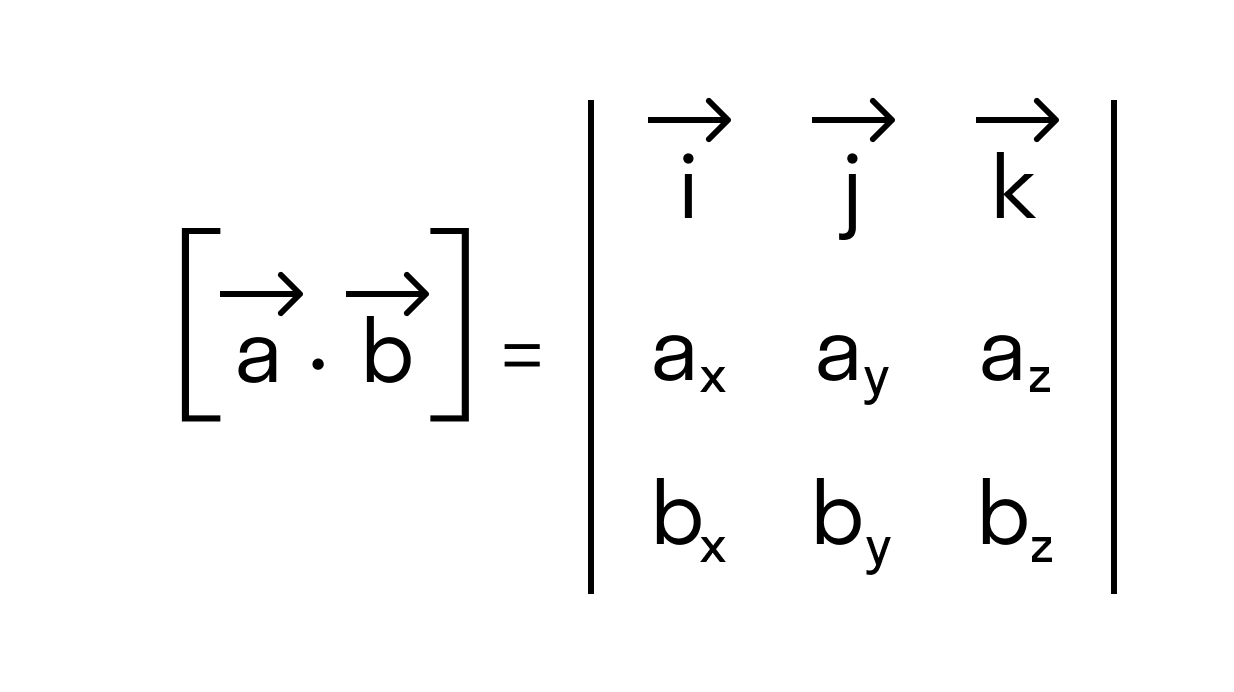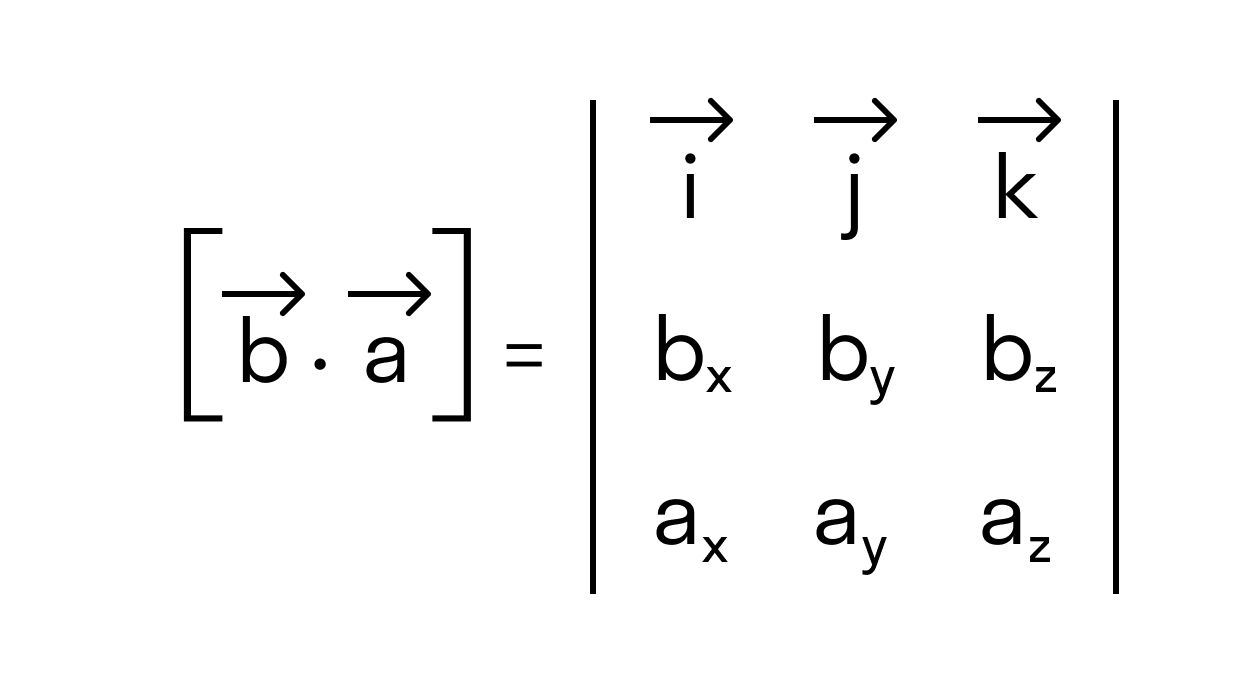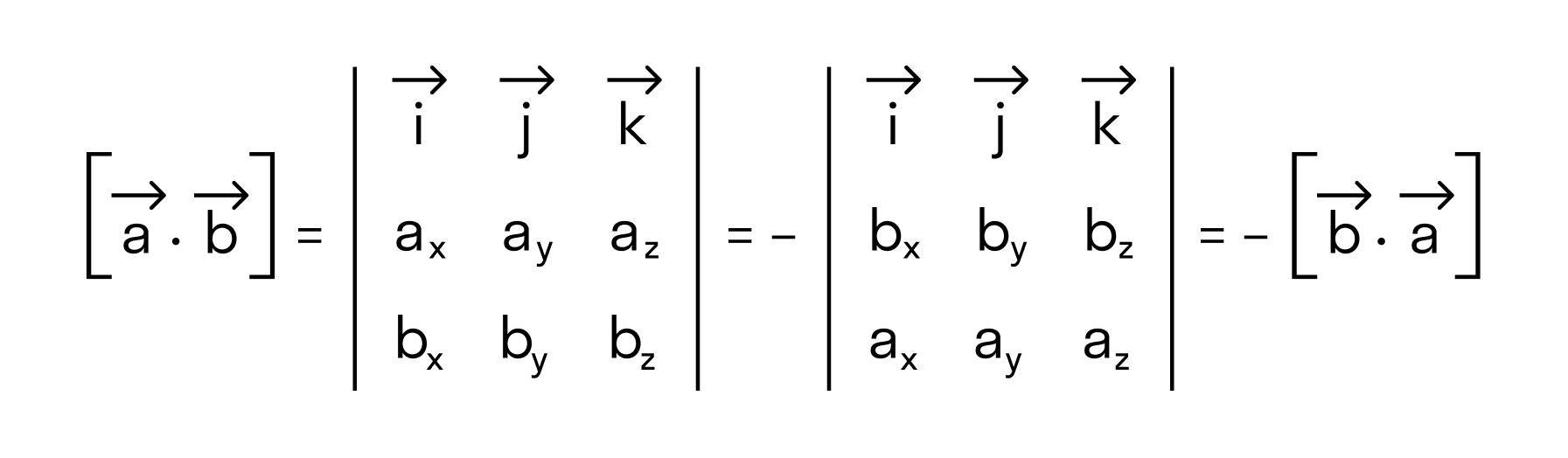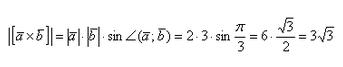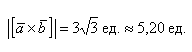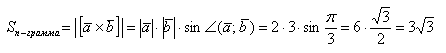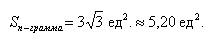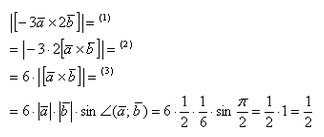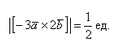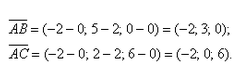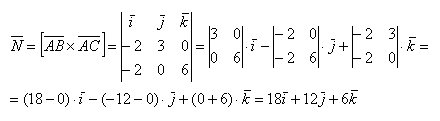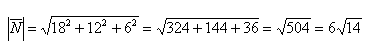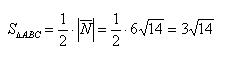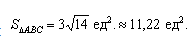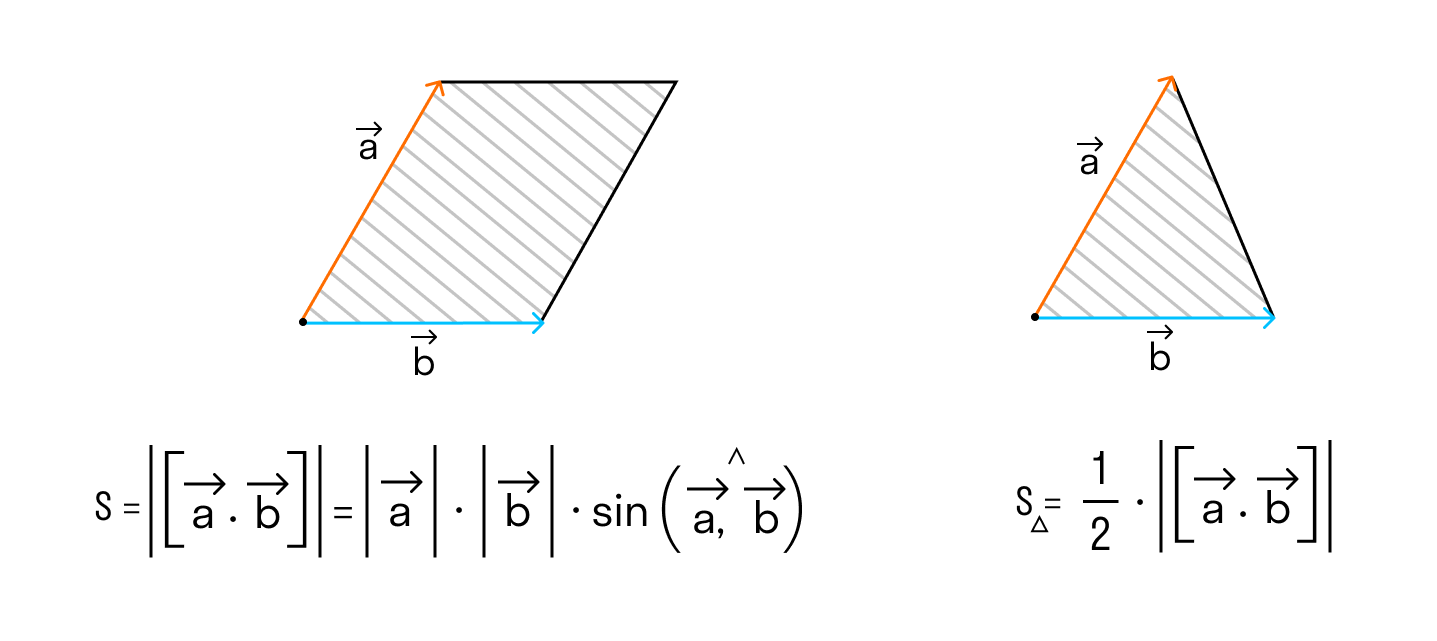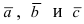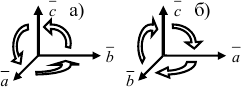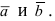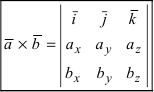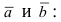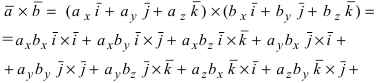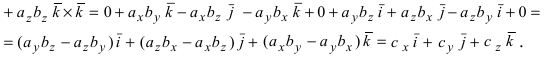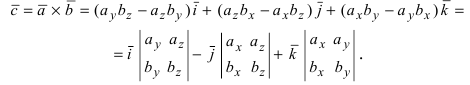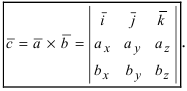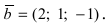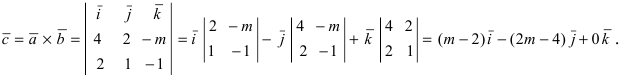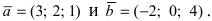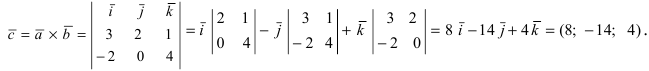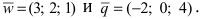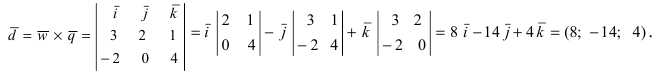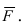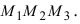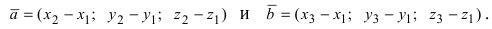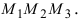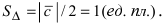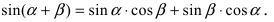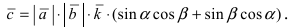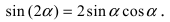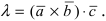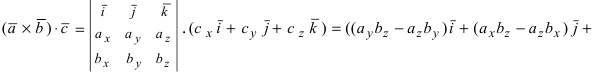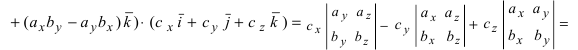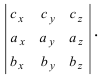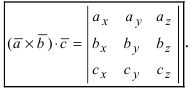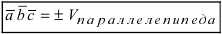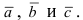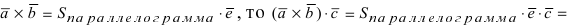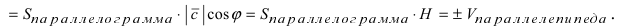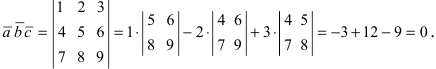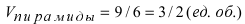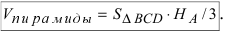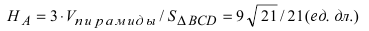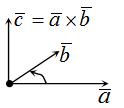Векторное произведение векторов
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
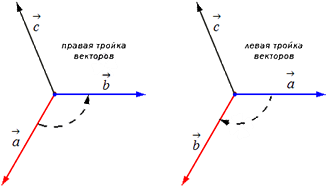
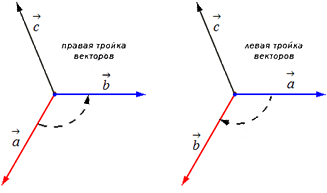
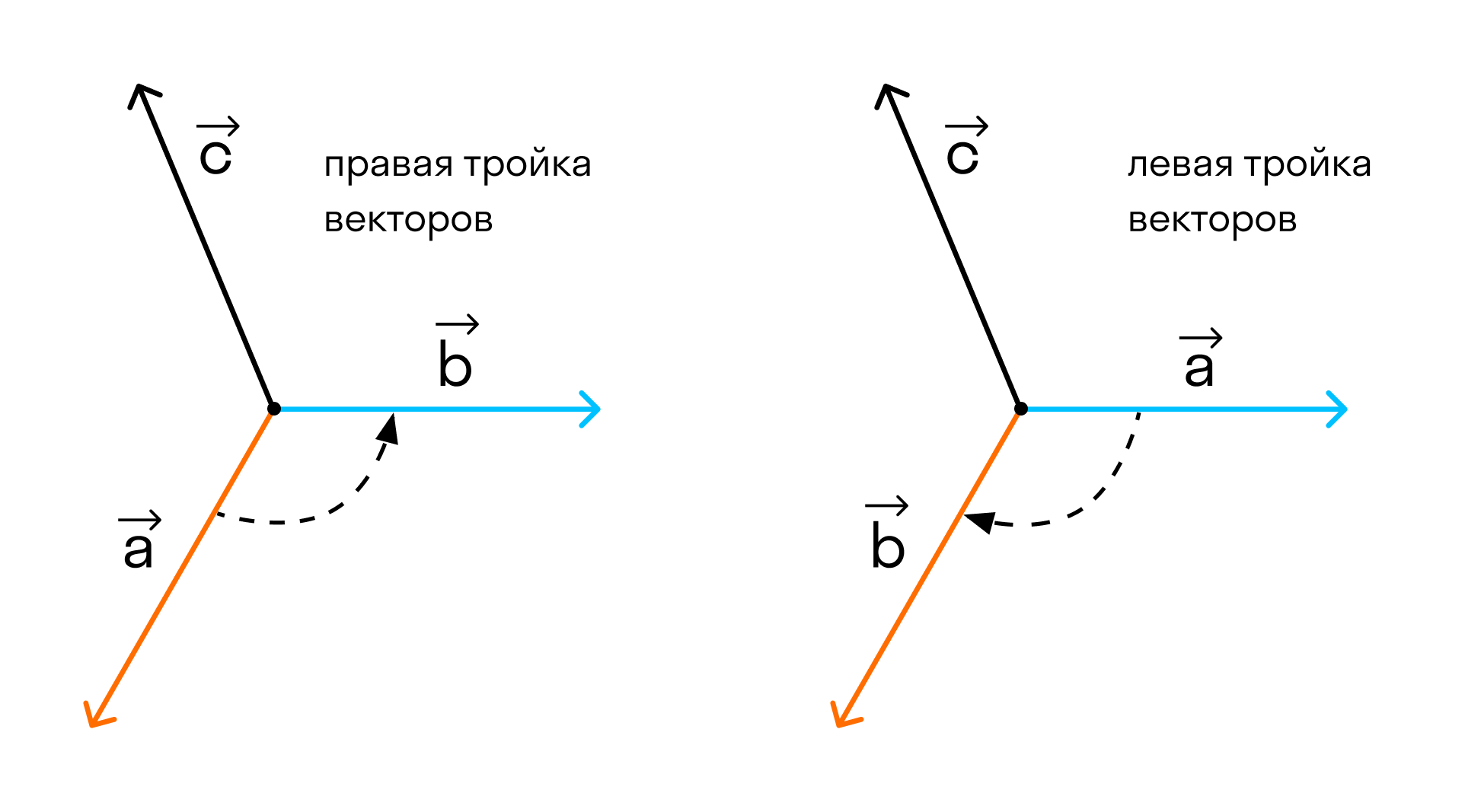
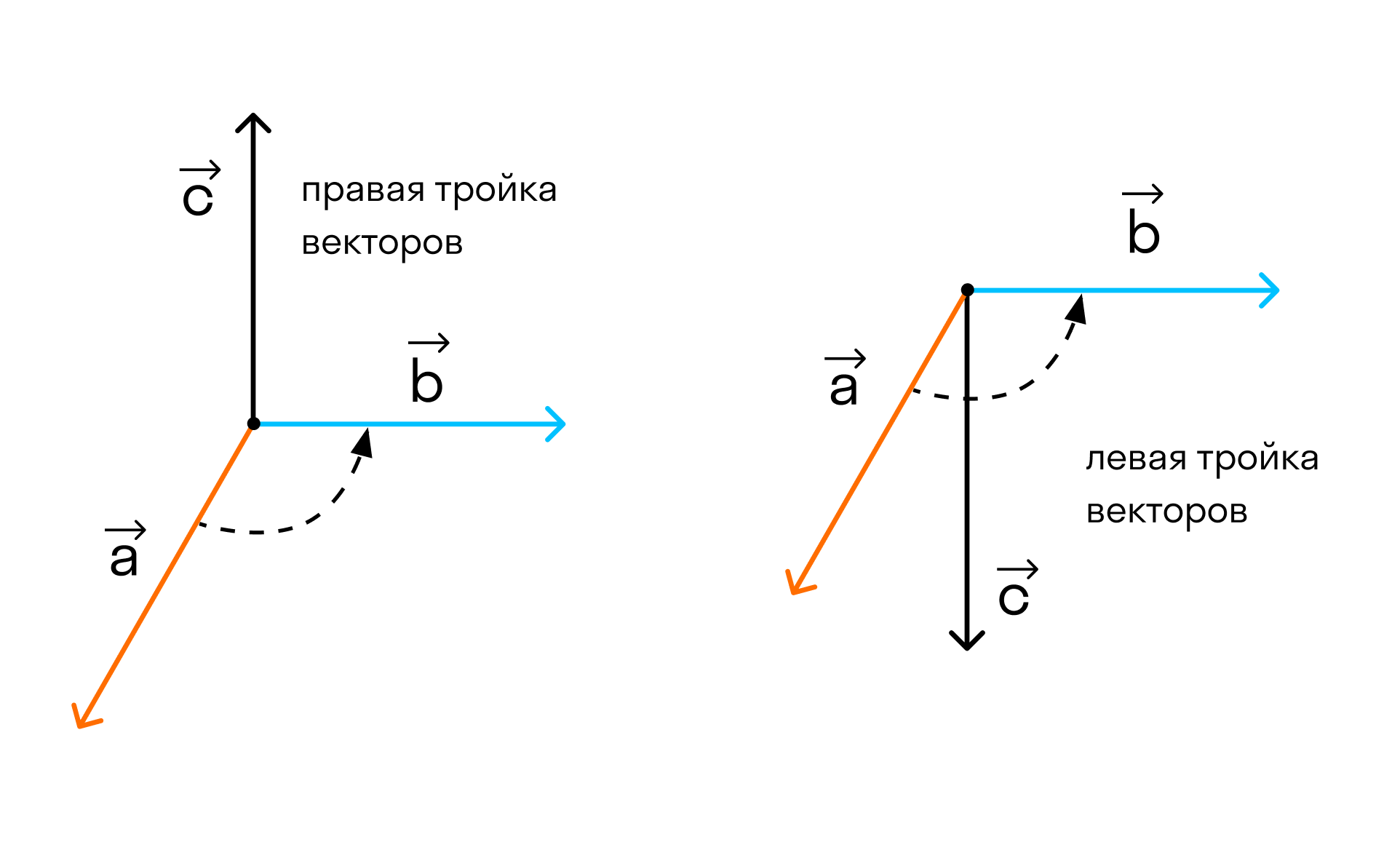
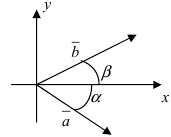
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
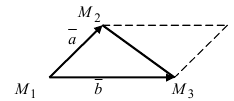
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
- он является нулевым, если векторы →a и →b коллинеарны;
- он перпендикулярен и вектору →a и вектору →b;
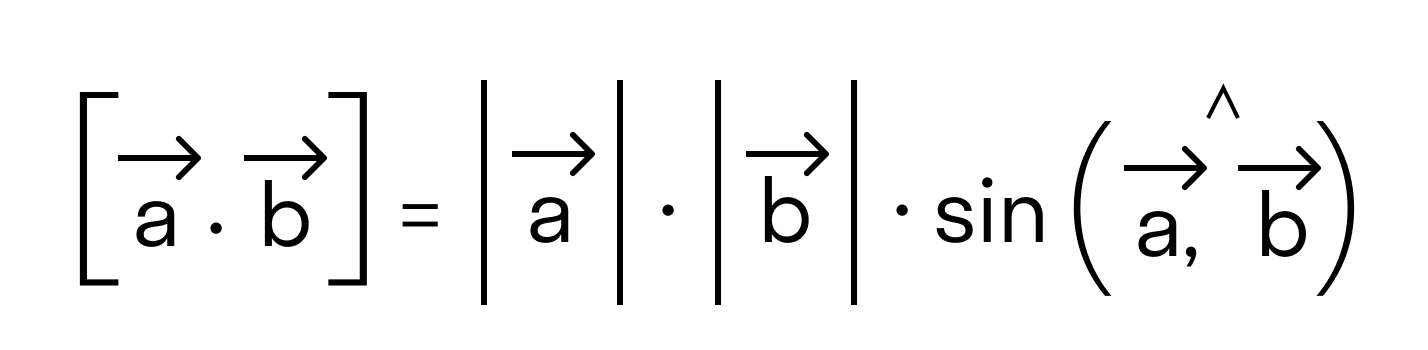
- длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
- тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.
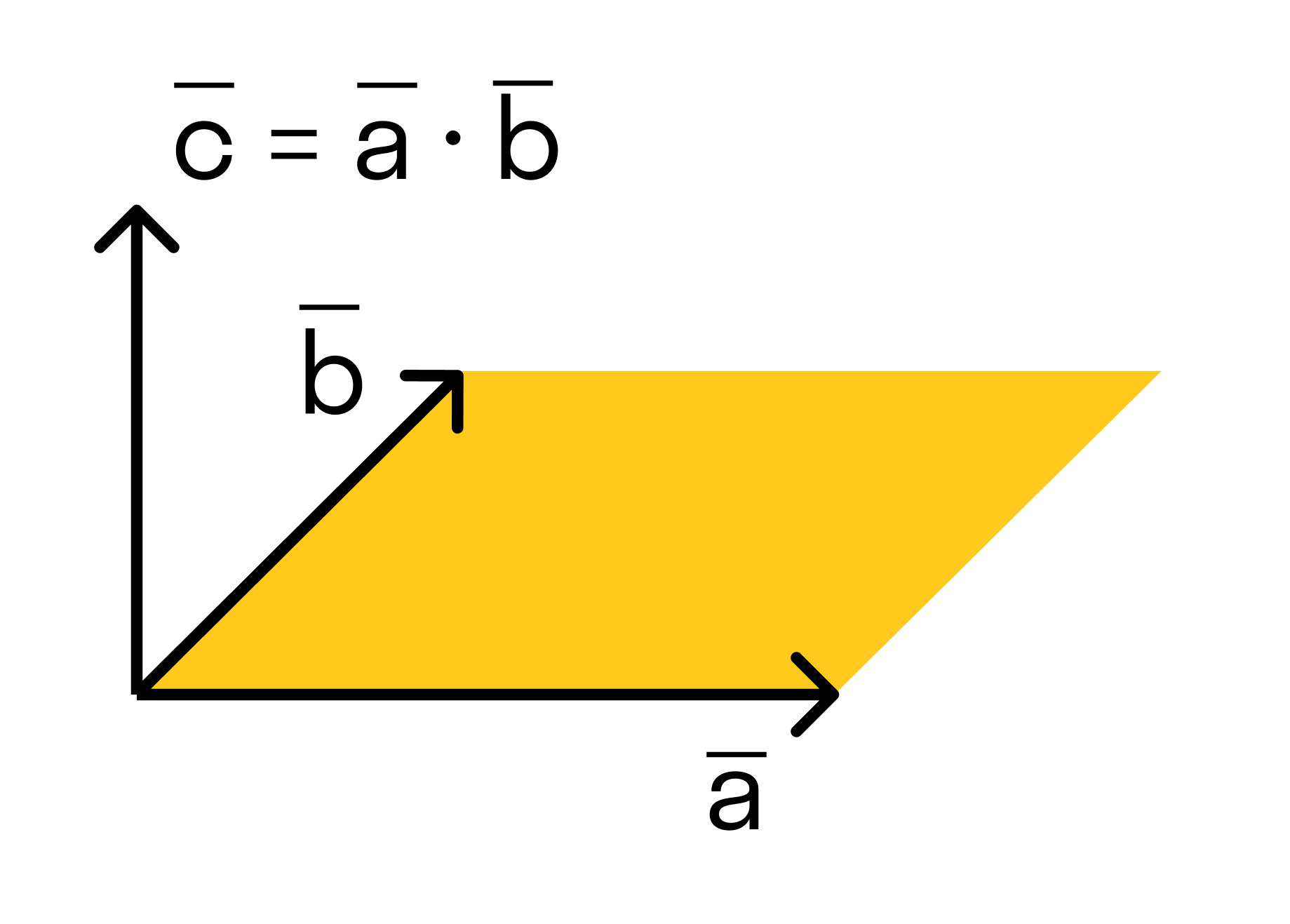
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a = и b = в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:
Векторное произведение векторов →a и →b обозначается как [→a • →b].
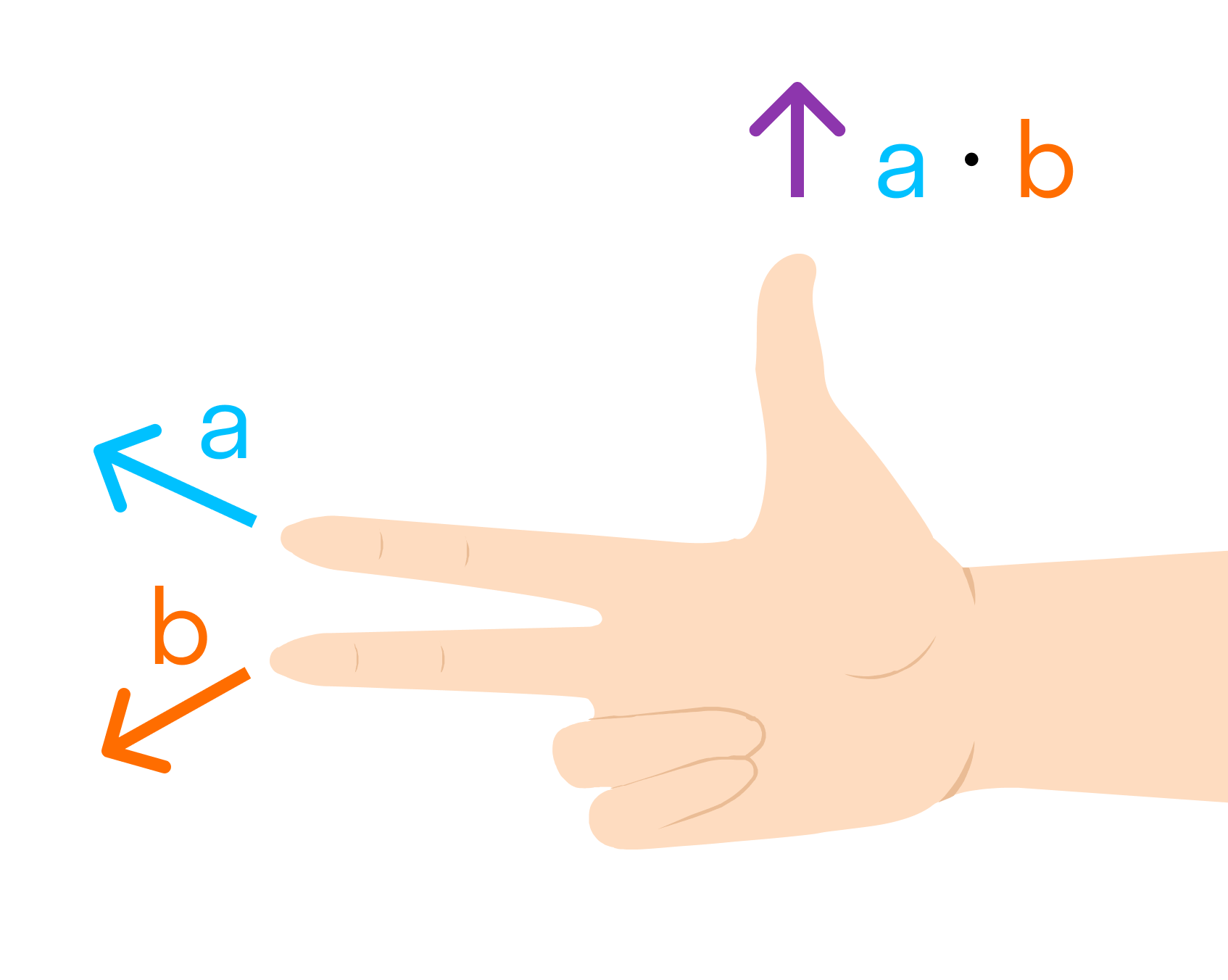
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
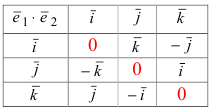
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
- Антикоммутативность
- Свойство дистрибутивности
Сочетательное свойство
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
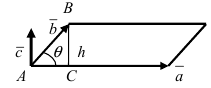
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
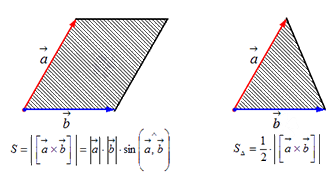
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
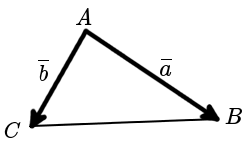
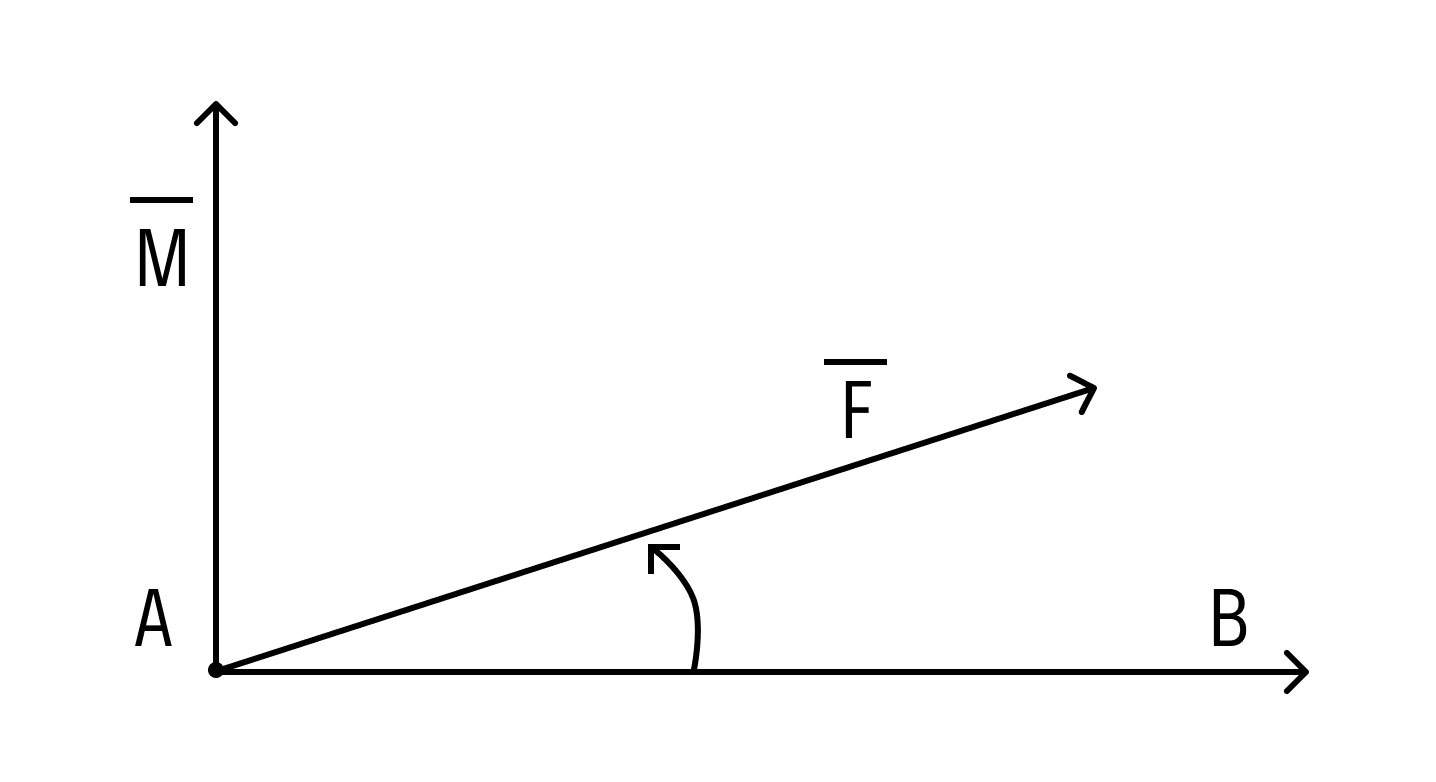
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
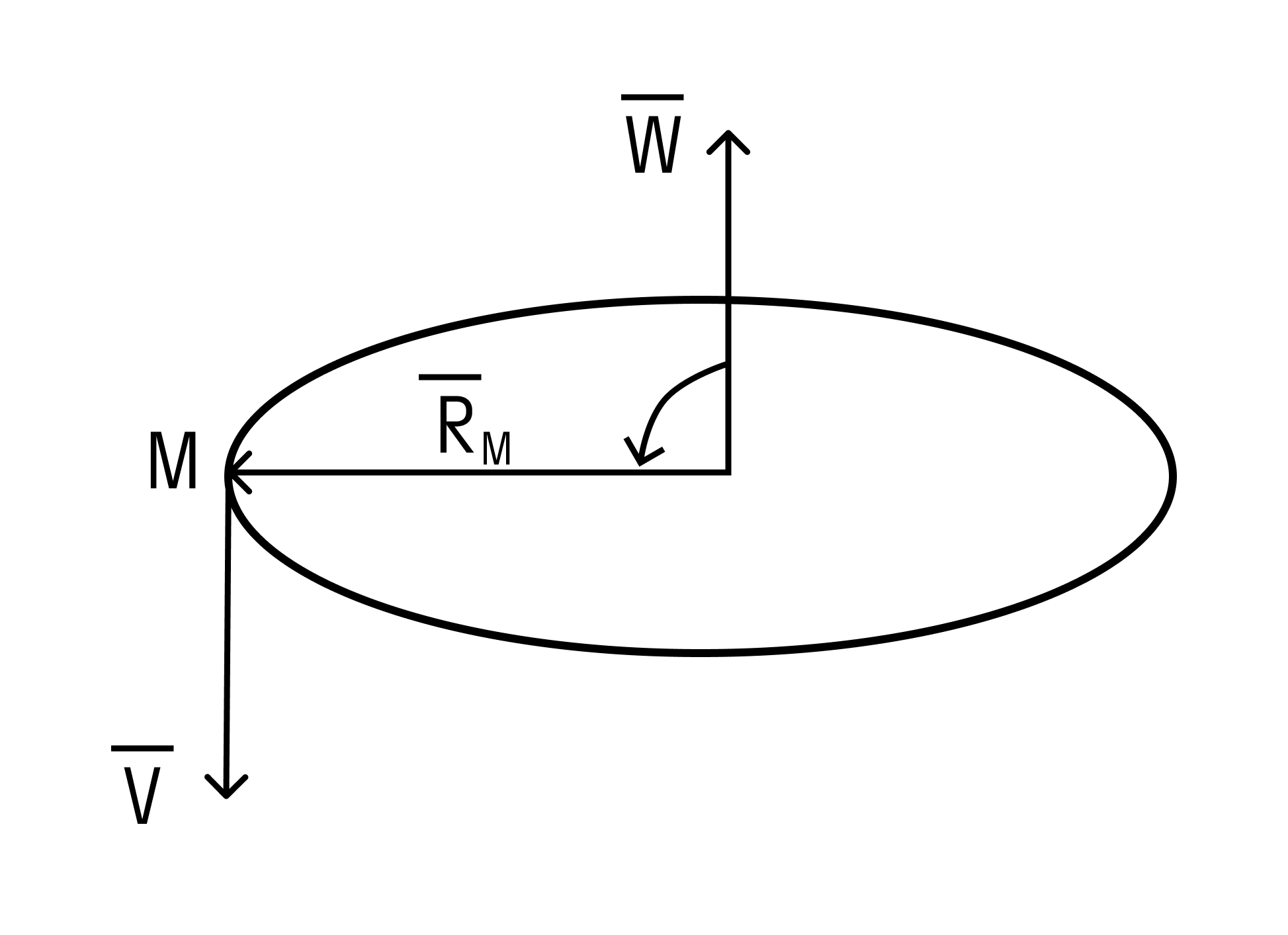
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
Векторное произведение — определения, свойства, формулы, примеры и решения
Определение векторного произведения
Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a → , b → , c → в трехмерном пространстве.
Отложим для начала векторы a → , b → , c → от одной точки. Ориентация тройки a → , b → , c → бывает правой или левой, в зависимости от направления самого вектора c → . От того, в какую сторону осуществляется кратчайший поворот от вектора a → к b → с конца вектора c → , будет определен вид тройки a → , b → , c → .
Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a → , b → , c → называется правой, если по часовой стрелке – левой.
Далее возьмем два не коллинеарных вектора a → и b → . Отложим затем от точки A векторы A B → = a → и A C → = b → . Построим вектор A D → = c → , который одновременно перпендикулярный одновременно и A B → и A C → . Таким образом, при построении самого вектора A D → = c → мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).
Упорядоченная тройка векторов a → , b → , c → может быть, как мы выяснили правой или левой в зависимости от направления вектора.
Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.
Векторным произведением двух векторов a → и b → будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:
- если векторы a → и b → коллинеарны, он будет нулевым;
- он будет перпендикулярен и вектору a → и вектору b → т.е. ∠ a → c → = ∠ b → c → = π 2 ;
- его длина определяется по формуле: c → = a → · b → · sin ∠ a → , b → ;
- тройка векторов a → , b → , c → имеет такую же ориентацию, что и заданная система координат.
Векторное произведение векторов a → и b → имеет следущее обозначение: a → × b → .
Координаты векторного произведения
Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.
В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a → = ( a x ; a y ; a z ) и b → = ( b x ; b y ; b z ) называют вектор c → = a → × b → = ( a y · b z — a z · b y ) · i → + ( a z · b x — a x · b z ) · j → + ( a x · b y — a y · b x ) · k → , где i → , j → , k → являются координатными векторами.
Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i → , j → , k → , вторая строка содержит координаты вектора a → , а третья – координаты вектора b → в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c → = a → × b → = i → j → k → a x a y a z b x b y b z
Разложив данный определитель по элементам первой строки, получим равенство: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k → = = a → × b → = ( a y · b z — a z · b y ) · i → + ( a z · b x — a x · b z ) · j → + ( a x · b y — a y · b x ) · k →
Свойства векторного произведения
Известно, что векторное произведение в координатах представляется как определитель матрицы c → = a → × b → = i → j → k → a x a y a z b x b y b z , то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:
- антикоммутативность a → × b → = — b → × a → ;
- дистрибутивность a ( 1 ) → + a ( 2 ) → × b = a ( 1 ) → × b → + a ( 2 ) → × b → или a → × b ( 1 ) → + b ( 2 ) → = a → × b ( 1 ) → + a → × b ( 2 ) → ;
- ассоциативность λ · a → × b → = λ · a → × b → или a → × ( λ · b → ) = λ · a → × b → , где λ — произвольное действительное число.
Данные свойства имеют не сложные доказательства.
Для примера можем доказать свойство антикоммутативности векторного произведения.
По определению a → × b → = i → j → k → a x a y a z b x b y b z и b → × a → = i → j → k → b x b y b z a x a y a z . А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно, a → × b → = i → j → k → a x a y a z b x b y b z = — i → j → k → b x b y b z a x a y a z = — b → × a → , что и доказывает антикоммутативность векторного произведения.
Векторное произведение – примеры и решения
В большинстве случаев встречаются три типа задач.
В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулой c → = a → · b → · sin ∠ a → , b → .
Найдите длину векторного произведения векторов a → и b → , если известно a → = 3 , b → = 5 , ∠ a → , b → = π 4 .
С помощью определения длины векторного произведения векторов a → и b → решим данную задач: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .
Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a → = ( a x ; a y ; a z ) и b → = ( b x ; b y ; b z ) .
Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов a → и b → , а их разложения по координатным векторам вида b → = b x · i → + b y · j → + b z · k → и c → = a → × b → = ( a y · b z — a z · b y ) · i → + ( a z · b x — a x · b z ) · j → + ( a x · b y — a y · b x ) · k → , или векторы a → и b → могут быть заданы координатами точек их начала и конца.
Рассмотрим следующие примеры.
В прямоугольной системе координат заданы два вектора a → = ( 2 ; 1 ; — 3 ) , b → = ( 0 ; — 1 ; 1 ) . Найдите их векторное произведение.
По второму определению найдем векторное произведение двух векторов в заданных координатах: a → × b → = ( a y · b z — a z · b y ) · i → + ( a z · b x — a x · b z ) · j → + ( a x · b y — a y · b x ) · k → = = ( 1 · 1 — ( — 3 ) · ( — 1 ) ) · i → + ( ( — 3 ) · 0 — 2 · 1 ) · j → + ( 2 · ( — 1 ) — 1 · 0 ) · k → = = — 2 i → — 2 j → — 2 k → .
Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 — 3 0 — 1 1 = — 2 i → — 2 j → — 2 k → .
Ответ: a → × b → = — 2 i → — 2 j → — 2 k → .
Найдите длину векторного произведения векторов i → — j → и i → + j → + k → , где i → , j → , k → — орты прямоугольной декартовой системы координат.
Для начала найдем координаты заданного векторного произведения i → — j → × i → + j → + k → в данной прямоугольной системе координат.
Известно, что векторы i → — j → и i → + j → + k → имеют координаты ( 1 ; — 1 ; 0 ) и ( 1 ; 1 ; 1 ) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i → — j → × i → + j → + k → = i → j → k → 1 — 1 0 1 1 1 = — i → — j → + 2 k → .
Следовательно, векторное произведение i → — j → × i → + j → + k → имеет координаты ( — 1 ; — 1 ; 2 ) в заданной системе координат.
Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i → — j → × i → + j → + k → = — 1 2 + — 1 2 + 2 2 = 6 .
Ответ: i → — j → × i → + j → + k → = 6 . .
В прямоугольной декартовой системе координат заданы координаты трех точек A ( 1 , 0 , 1 ) , B ( 0 , 2 , 3 ) , C ( 1 , 4 , 2 ) . Найдите какой-нибудь вектор, перпендикулярный A B → и A C → одновременно.
Векторы A B → и A C → имеют следующие координаты ( — 1 ; 2 ; 2 ) и ( 0 ; 4 ; 1 ) соответственно. Найдя векторное произведение векторов A B → и A C → , очевидно, что оно является перпендикулярным вектором по определению и к A B → и к A C → , то есть, является решением нашей задачи. Найдем его A B → × A C → = i → j → k → — 1 2 2 0 4 1 = — 6 i → + j → — 4 k → .
Ответ: — 6 i → + j → — 4 k → . — один из перпендикулярных векторов.
Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.
Векторы a → и b → перпендикулярны и их длины равны соответственно 3 и 4 . Найдите длину векторного произведения 3 · a → — b → × a → — 2 · b → = 3 · a → × a → — 2 · b → + — b → × a → — 2 · b → = = 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b → .
По свойству дистрибутивности векторного произведения мы можем записать 3 · a → — b → × a → — 2 · b → = 3 · a → × a → — 2 · b → + — b → × a → — 2 · b → = = 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b →
По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b → = = 3 · a → × a → + 3 · ( — 2 ) · a → × b → + ( — 1 ) · b → × a → + ( — 1 ) · ( — 2 ) · b → × b → = = 3 · a → × a → — 6 · a → × b → — b → × a → + 2 · b → × b →
Векторные произведения a → × a → и b → × b → равны 0, так как a → × a → = a → · a → · sin 0 = 0 и b → × b → = b → · b → · sin 0 = 0 , тогда 3 · a → × a → — 6 · a → × b → — b → × a → + 2 · b → × b → = — 6 · a → × b → — b → × a → . .
Из антикоммутативности векторного произведения следует — 6 · a → × b → — b → × a → = — 6 · a → × b → — ( — 1 ) · a → × b → = — 5 · a → × b → . .
Воспользовавшись свойствами векторного произведения, получаем равенство 3 · a → — b → × a → — 2 · b → = = — 5 · a → × b → .
По условию векторы a → и b → перпендикулярны, то есть угол между ними равен π 2 . Теперь остается лишь подставить найденные значения в соответствующие формулы: 3 · a → — b → × a → — 2 · b → = — 5 · a → × b → = = 5 · a → × b → = 5 · a → · b → · sin ( a → , b → ) = 5 · 3 · 4 · sin π 2 = 60 .
Ответ: 3 · a → — b → × a → — 2 · b → = 60 .
Геометрический смысл векторного произведения
Длина векторного произведения векторов по орпеделению равна a → × b → = a → · b → · sin ∠ a → , b → . Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма — удвоенного треугольника, а именно произведению сторон в виде векторов a → и b → , отложенные от одной точки, на синус угла между ними sin ∠ a → , b → .
Это и есть геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.
Под моментом силы F → , приложенной к точке B , относительно точки A будем понимать следующее векторное произведение A B → × F → .
Векторное произведение векторов.
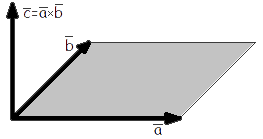 |
| рис. 1 |
Формулы вычисления векторного произведения векторов
Векторное произведение двух векторов a = < ax ; ay ; az > и b = < bx ; by ; bz > в декартовой системе координат — это вектор, значение которого можно вычислить, используя следующие формулы:
Свойства векторного произведения векторов
Примеры задач на вычисления векторного произведения векторов
| a × b = | i | j | k | = |
| 1 | 2 | 3 | ||
| 2 | 1 | -2 |
= i (2 · (-2) — 3 · 1) — j (1 · (-2) — 2 · 3) + k (1 · 1 — 2 · 2) =
Решение: Найдем векторное произведение этих векторов:
| a × b = | i | j | k | = |
| -1 | 2 | -2 | ||
| 2 | 1 | -1 |
= i (2 · (-1) — (-2) · 1) — j ((-1) · (-1) — (-2) · 2) + k ((-1) · 1 — 2 · 2) =
Из свойств векторного произведения:
SΔ = 1 2 | a × b | = 1 2 √ 0 2 + 5 2 + 5 2 = 1 2 √ 25 + 25 = 1 2 √ 50 = 5√ 2 2 = 2.5√ 2
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
http://zaochnik.com/spravochnik/matematika/vektory/vectornoe_proizvedenie/
http://ru.onlinemschool.com/math/library/vector/multiply1/
Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает
обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:
Векторное произведение векторов →a и →b обозначается как [→a • →b].
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
, где
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
- Антикоммутативность
- Свойство дистрибутивности
или
- Сочетательное свойство
или
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
По определению
и
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
Как решаем:
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Ответ:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Ответ:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
Как решаем:
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Ответ:
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Как решаем:
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Ответ:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
Содержание:
Векторное и смешанное произведения векторов в векторной алгебре
Векторное произведение
Определение: Тройка векторов
Пример:
Рис. 13. Правая (а) и левая (б) тройки векторов.
Определение: Векторным произведением векторов 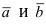
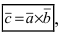
Замечание: Из определения векторного произведения следует, что направление вектора 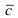
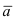
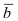
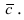
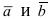
Рис. 14. Площадь параллелограмма, определяющего длину вектора 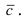
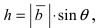
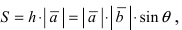
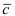
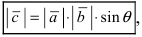
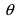
Векторное произведение векторов обладает следующими свойствами:
Замечание: Свойство 4. определяет второе условие коллинеарности векторов.
Формула для векторного произведения векторов через проекции перемножаемых векторов
Теорема: Пусть 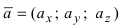
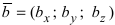
Доказательство: Запишем вектора 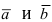
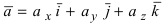
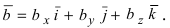
Используя эту таблицу, вычислим векторное произведение векторов
Отсюда следует, что 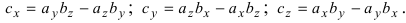
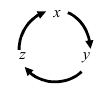
Рис. 15. Циклический переход от одной координаты к другой.
Для нахождения, например проекции 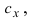
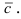
Полученное выражение представляет собой раскрытие определителя III порядка по элементам первой строки, то есть окончательно можно записать, что
Пример:
Найти, при каком значении параметра m вектор 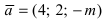
Решение:
Согласно свойству 4. для векторного произведения (пункт 1 Лекция № 6) найдем векторное произведение заданных векторов
Так как вектор 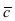
- Заказать решение задач по высшей математике
Пример:
Найти векторное произведение векторов
Решение:
Пример:
Найти векторное произведение векторов
Решение:
Приложения векторного произведения
1. Физика. Пусть точка начала вектора 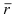
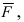
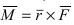
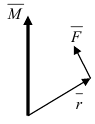
2. Геометрия. Пусть даны три разные точки 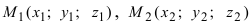
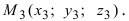
Введем в рассмотрение вектора 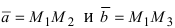
Рис. 17. Площадь треугольника
Проекции этих векторов равны:
Так как площадь треугольника составляет половину от площади параллелограмма, площадь которого равна модулю векторного произведения векторов 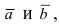
Пример:
Даны три точки 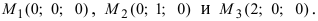
Решение:
Введем в рассмотрение вектора 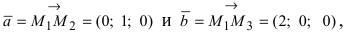
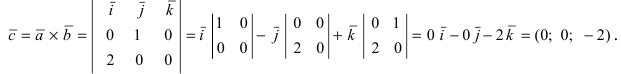
3. Тригонометрия. Выведем формулу для
Пусть в плоской декартовой системе координат даны векторы 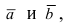
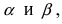
Рис. 18. Синус суммы двух углов.
Проекции векторов равны 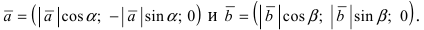
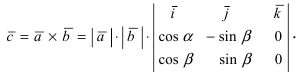
Длина этого вектора равна 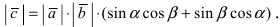
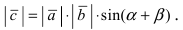
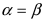
Смешанное произведение векторов
Определение: Смешанным произведением векторов 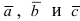
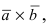
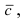
Получим формулу для вычисления смешанного произведения
Обменяв местами первую строку со второй, а затем и с третьей, получим окончательную формулу
Таким образом, смешанное произведение векторов представляет собой определитель III порядка, откуда следуют его свойства:
1. 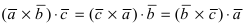
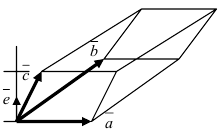
2. Смешанное произведение векторов 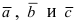
Рис. 19. Объем параллелепипеда, построенного на векторах
Так как
3. Если вектора 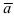
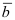
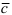
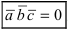
Замечание: Свойство 3. определяет условие компланарности трех векторов, т.е. если 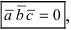
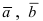
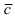
Пример:
Доказать, что вектора 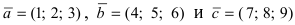
Решение:
Согласно формуле, определяющей смешанное произведение векторов, имеем
Пример:
Даны 4 точки 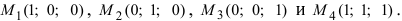
Решение:
Составим векторы 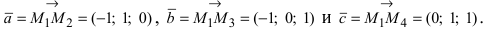
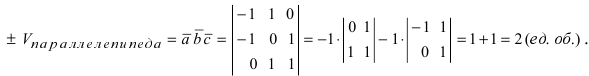
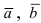
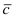
Пример:
Чему равен объём пирамиды с вершинами А, В, С и D (координаты точек А, В, С и D взять из VIII.). Найти длину высоту, которая опущена из точки А на основание BCD.
Решение:
Объём пирамиды равен 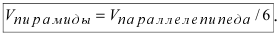
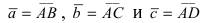
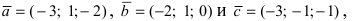
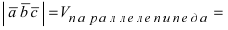
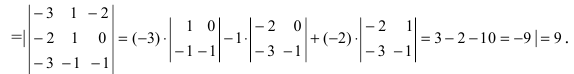
С другой стороны, её объём по формуле из средней школы равен
Вычислим площадь треугольника BCD, лежащего в основании пирамиды: 
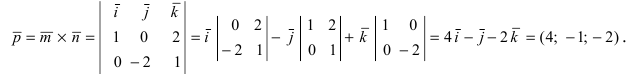
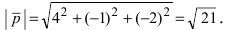
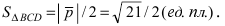
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Матричный метод
- Экстремум функции
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
Заказать задачи по любым предметам можно здесь от 10 минут
Векторное произведение векторов
Определение
| Определение |
|
Векторным произведением векторов $ overline{a} $ и $ overline{b} $ является вектор $ overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ overline{a} $ и $ overline{b} $. Само произведение обозначается как $ [overline{a},overline{b}] $, либо $ overline{a} times overline{b} $. |
Векторное произведение векторов, формула которого зависит от исходных данных задачи, можно найти двумя способами.
Формула
| Формула 1 |
|
Если известен синус угла между векторами $ overline{a} $ и $ overline{b} $, то найти векторное произведение векторов можно по формуле: $$ [overline{a},overline{b}] = |overline{a}| cdot |overline{b}| cdot sin (overline{a},overline{b}) $$ |
| Формула 2 |
|
В случае когда векторы $ overline{a} $ и $ overline{b} $ заданы в координатной форме, то их произведение определяется по формуле: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} $$ где векторы $ overline{i},overline{j},overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $. |
Определитель во второй формуле можно раскрыть по первой строке:
$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} = overline{i} (a_2 b_3 — a_3 b_2) — overline{j} (a_1 b_3 — a_3 b_1) + overline{k} (a_1 b_2 — a_2 b_1) $$
Итого вторая формула приобретает окончательный короткий вид:
$$ overline{a} times overline{b} = (a_2 b_3 — a_3 b_2; a_3 b_1 — a_1 b_3; a_1 b_2 — a_2 b_1) $$
Свойства
- При изменении порядка множителей меняется знак на противоположный: $$ [overline{a},overline{b}] = -[overline{b},overline{a}] $$
- Вынос константы за знак произведения: $$ lambda [overline{a},overline{b}] = [lambda overline{a}, overline{b}] = [overline{a}, lambda overline{b}] $$
- $$ [overline{a}+overline{b}, overline{c}] = [overline{a},overline{c}] + [overline{b}, overline{c}] $$
Примеры решений
| Пример 1 |
|
Найти векторное произведение векторов, заданных координатами $$ overline{a} = (2,1,-3) $$ $$ overline{b} = (1,2,-1) $$ |
| Решение |
|
Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ overline{a} $ и $ overline{b} $: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ 2&1&-3\1&2&-1 end{vmatrix} = overline{i} (-1+6) — overline{j}(-2+3) + overline{k}(4-1) = 5overline{i} — overline{j} + 3overline{k} $$ Полученный ответ можно записать в удобном виде: $$ overline{a} times overline{b} = (5, -1, 3) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ overline{a} times overline{b} = (5, -1, 3) $$ |
Геометрический смысл
- Модуль векторного произведения векторов $ overline{a} $ и $ overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |overline{a} times overline{b}| $$
- Половина этого модуля это площадь треугольника: $$ S_Delta = frac{1}{2} |overline{a} times overline{b} | $$
- Если векторное произведение равно нулю $ overline{a} times overline{b} = 0 $, то векторы коллинеарны.
| Пример 2 |
| Найти площадь треугольника по заданным векторам $$ overline{a} = (2,1,3) $$ $$ overline{b} = (-1,2,1) $$ |
| Решение |
|
Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов. Находим определитель: $$ begin{vmatrix} overline{i}&overline{j}&overline{k}\2&1&3\-1&2&1 end{vmatrix} = overline{i}(1-6) — overline{j}(2+3) + overline{k}(4+1) = -5overline{i} — 5overline{j} + 5overline{k} $$ Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора: $$ |overline{a} times overline{b}| = sqrt{(-5)^2 + (-5)^2 + 5^2} = sqrt{25 + 25 + 25} = sqrt{75} $$ По формуле нахождения площади треугольника имеем: $$ S_Delta = frac{1}{2} |overline{a} times overline{b}| = frac{1}{2} sqrt{75} = 4.33 $$ |
| Ответ |
| $$ S_Delta = 4.33 $$ |
Содержание:
- Переходим к понятию векторного произведения
- Некоторые приложения к механике векторов
В векторной алгебре наряду с умножением вектора на скаляр 

Напомним 

направление его обхода. Обратно, если указывается направление обхода контура, это приводит к ориентации самой поверхности. Связь между ориентацией поверхности и ориентацией ее контура указана па рис. 134; если за основу системы координат взята правая тройка векторов 
Например, правило правого винта можно сформулировать так: если правый винт (который обычно применяется в технике и обыденной жизни) вращать в направлении обхода контура, то винт должен пойти от внутренней стороны поверхности к наружной. Или, другими словами: если маленький человечек обходит по наружной стороне поверхности ее контур по указанному направлению обхода, то сама поверхность должна быть у него но левую руку*).
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Переходим к понятию векторного произведения
Векторное произведение двух векторов 






Где принято правило правого винта, которым мы всегда будем пользоваться, если не оговорено противное).
Таким образом, векторное произведение двух векторов 









Векторное произведение «аитикоммутативно» **)

Действительно, при перемене порядка множителей параллелограмм не изменится, но контур его будет проходиться в противоположном направлении и потому вектор площадки заменится на противоположный.
Можно проверить, что скалярный множитель можно выносить за знак векторного произведения:

на что справедлив распределительный закон:

Раскрывая скобки в выражениях, включающих векторное произведение, надо тщательно следить за порядком множителей. Приведем пример:
Пусть векторы 

Тогда, если воспользоваться равенствами (проверьте их!)
получим

(продумайте структуру последнего выражения!).
Этот результат очень просто запомнить, если записать его в виде определителя (см. формулу
Пусть, например, надо вычислить площадь 



Так как в этом примере векторы 

Иногда применяется также векторно-скалярное или, иначе, смешанное произведение трех векторов 


т. е. смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах. На рис. 138 векторы

образуют правую тройку, и получился объем со знаком плюс. Для левой тройки угол между 


Легко получить выражение для смешанного иризведенпя в случае, с ели даны разложения сомножителей в декартовой системе координат. Для этого нужно правую часть (2) помножить обычным способом скалярнп (по формуле (IX,5)) на вектор 
Нам понадобится еще формула для векторно-векторного произведения 









Этот результат неудобен тем, что «привязан» к специальному выбору осей координат. Поэтому преобразуем его (проверьте)):
Эта формула уже не содержит координатных проекций, а потому не зависит от специального выбора системы координат.
Возможно вам будут полезны данные страницы:
Примеры с решением
Пример 1.
Определим векторное произведение векторов 

Векторное произведение векторов 

Пример 2.
Даны точки 

Из геометрического смысла векторного произведения векторов следует, что площадь треугольника 

Тогда векторное произведение векторов 





Пример 3.
Вектор 





Из свойств векторного произведения векторов получаем что векторное произведение 



Тогда модуль векторного произведения 

Так как векторы 
Пусть 


Так как вектор 

Тогда 






Тогда вектор
Некоторые приложения к механике векторов
Векторное произведение особенно удобно при описании вращательного движения и связанных с ним понятий. Рассмотрим вращение твердого тела вокруг некоторой оси (рис. 137) 




— безразлично; такой вектор, который можно произвольно перемещать вдоль некоторой оси, но не в сторону от этой оси, называется скользящим*).
Будем ‘ считать, что начало координа 












(проверьте, что векторное произведение надо брать именно в выписанном порядке п что правая часть (5) не зависит от конкретного выбора точки 
Удобство вектора угловой скорости видно, в частности, из следующего. Допустим, что тело испытывает одновременно два вращения с (вообще говоря, непараллельными) векторами угловой скорости 






С помощью векторного произведения вводится такое важное понятие, как момент произвольного вектора 






При вычислении момента вектора этот вектор можно считать скользящим. В самом деле, если вектор 




Если же вектор относить в сторону относительно его направления, то момент изменяется.
Рассмотрим систему как-то связанных между собой материальных частиц, каждая из которых имеет постоянную массу 




Поэтому сумма всех внутренних сил, а также сумма их моментов относительно любой точки равны нулю.
Основные уравнения движения системы частиц получаются, если записать второй закон Ньютона («сила равна произведению массы на ускорение 
Если просуммировать эти равенства по всем частицам, получим

гак как сумма всех внутренних сил, как было сказано выше, равна пулю. Удобно ввести точку 


Итак, центр масс движется гак, как будто он обладает полной массой системы и на него действует сила, равная сумме всех внешних сил. В частности, если внешние силы отсутствуют, то центр масс системы движется прямолинейно и равномерно, 
Перейдем к моментам. Если обе части равенства (6) умножить слева векторпо на 
Воспользуемся равенством

эта формула 

Суммируя эти равенства по всем 
так как сумма моментов всех внутренних сил равна нулю. Сумма
моментов количества движения всех частиц, составляющих систему, называется кинетическим моментом (моментом вращения) этой системы относительно той же точки 

т. е. скорость изменения кинетического момента системы равна полному моменту внешних сил, действующих на эту систему. В частном случае, если внешние силы отсутствуют или если их полный момент равен нулю, получаем, что кинетический момент системы остается постоянным.
Лекции:
- Таблица производных полная: для студентов
- Функции двух переменных. Действия над случайными величинами
- Найти значение выражения
- Исследование графика функции
- Существование предела
- Ранг матрицы: примеры решения
- Найдите объем тела ограниченного
- Разложение вектора по базису
- Умножение матрицы на вектор
- Циркуляция векторного поля. Ротор вектора. Теорема Стокса