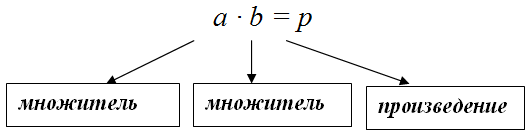
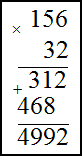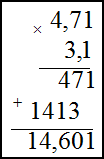Как найти произведение если есть сумма - Avtoru.top

Как найти произведение суммы

Сложение и умножение — базовые математические операции, стоящие в одном ряду с вычитанием, делением, возведением в степень, и другими. Комбинируя эти операции между собой, можно получить новые, более сложные операции.

Инструкция

Чтобы умножить сумму на число, перемножьте каждое слагаемое с этим числом, полученные числа сложите между собой.Пример. (a+b+c)*p=a*p+b*p+c*p.Обратная операция — вынесение общего множителя за скобку: a*p+b*p+c*p=p(a+b+c).

Для перемножения двух скобок, содержащих в себе суммы каких-то переменных, существует определенная схема. Надо умножить сначала слагаемое первой скобки на каждое из слагаемых второй скобки, сложить полученные результаты, затем ту же операцию проделать со вторым и последующими слагаемыми первой скобки. Осталось сложить полученные числа между собой.Пример.(a+b)*(c+d)=a*c+a*d+b*c+b*d.Помните, что перемножаются также и знаки перед числами. Произведение одинаковых знаков дает плюс, разных знаков — минус. Например, (a-b)(c+d)=a*c+a*d-b*c-b*d; (a-b)(c-d)=a*c-a*d-b*c+b*d.Обратная операция — разложение суммы на множители.

Чтобы перемножить три скобки, являющиеся суммами некоторых переменных, надо перемножить сначала любые две скобки, затем полученный результат умножить на третью скобку. Умножение четырех и большего числа скобок происходит аналогично. Группируйте скобки так, чтобы считать было удобнее и проще.

Частный случай произведения сумм — возведение суммы в степень. Например, (a+b)^2, (c-d)^3, (p-k)^6. Можно представить возведение в степень в виде произведения нескольких одинаковых скобок и перемножать их по правилам, изложенным выше. А можно воспользоваться формулами сокращенного умножения, которые всегда полезно помнить.

Видео по теме

Полезный совет

Выведите самостоятельно формулы сокращенного умножения, последовательно перемножая скобки. Это позволит лучше понять суть происходящего, а заодно потренироваться в умножении сумм.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

DrSMERTb

64 / 40 / 10

Регистрация: 12.11.2010

Сообщений: 841

09.03.2014, 16:42

[ТС]

Сообщение было отмечено Taatshi как решение

Решение

rrrFer, вот так переделал,

Prolog

predicates
        start
        summ(integer,integer,integer) /*A=B*N (A,B,N)*/
clauses      
    summ(A,B,N):-
        NN=N-1,
        NN>=0,
        AA=B+B,
        summ(AA,B,NN). 
    start:-
        write("A=B*N"),nl,
        write("B: "),readint(B),
        write("N: "),readint(N),
        summ(A,B,N),
        write(A),nl.
goal
    start

Только чот не пойму как описать остановку итераций, т.е. когда N приравняется к 0. Может можете поправить код?)

Добавлено через 1 час 26 минут
Добавил правило для умножения на ноль. Но не получается установить правило при умножении на 1.

Prolog

1
2
3

Clauses
           sum(0,_,0).   %Работает
           sum(B,B,1).   %не робит

Как прописать второе правило?

Добавлено через 23 минуты
Всё доделал, конечный вариант

Prolog

        Domains
           A,B,N=real
        Predicates
           sum(A,B,N)
           start
        Clauses
           sum(0,_,0).
           sum(A,B,N):-N>0,N1=N-1,sum(A1,B,N1),A=A1+B.
start:-
        write("A=B*N"),nl,
        write("Введите первое число: "),readint(B),
        write("Введите втрое число: "),readint(N),
        sum(A,B,N),
        write("Ответ: ",B," * ",N," = ",A),nl.
goal
    start

Источник

Умножение числа на сумму

Примеры

Умножить число на сумму можно двумя способами:

1) Чтобы умножить число на сумму, можно сначала выполнить сложение, а затем умножить число на полученный результат.

Например, чтобы найти значение выражения:

4 · (3 + 5),

можно сначала сложить числа 3 и 5:

3 + 5 = 8

и число 4 умножить на полученный результат:

4 · 8 = 32, значит

4 · (3 + 5) = 4 · 8 = 32.

2) Для умножения числа на сумму, можно умножить данное число на каждое слагаемое отдельно и полученные результаты сложить.

Например, чтобы найти значение выражения:

4 · (3 + 5),

можно отдельно умножить число 4 на 3 и на 5:

4 · 3 = 12 и 4 · 5 = 20

и полученные произведения сложить:

12 + 20 = 32, значит

4 · (3 + 5) = 4 · 3 + 4 · 5 = 12 + 20 = 32.

Данные способы умножения числа на сумму можно легко проверить, посчитав количество звёздочек на картинке:

Не важно как мы будем их считать:

пересчитывать все по порядку;
считать количество звёздочек в строке и умножать количество строк на полученный результат;
считать сначала количество жёлтых звёздочек, затем зелёных, и складывать полученный результаты.

При любом способе счёта получится ровно 32 звёздочки.

Умножение числа на сумму можно представить в виде общей формулы:

a · (b + c) = a · b + a · c.

Данная формула выражает распределительный закон умножения.

Примеры

Пример 1. Найти значение каждого выражения двумя способами:

a) 2 · (3 + 8);

b) 5 · (6 + 3);

c) 3 · (1 + 4).

Решение:

a) 2 · (3 + = 22;

2 · (3 + = 2 · 11 = 22;
2 · (3 + = 2 · 3 + 2 · 8 = 6 + 16 = 22.

b) 5 · (6 + 3) = 45;

5 · (6 + 3) = 5 · 9 = 45;
5 · (6 + 3) = 5 · 6 + 5 · 3 = 30 + 15 = 45.

c) 3 · (1 + 4) = 15;

3 · (1 + 4) = 3 · 5 = 15;
3 · (1 + 4) = 3 · 1 + 3 · 4 = 3 + 12 = 15.

Пример 2. Вычислить, удобным способом:

1) 5 · (4 + 6);

2) 2 · (32 + 13);

3) 7 · (10 + 5).

Решение:

1) 5 · (4 + 6) = 5 · 10 = 50;

2) 2 · (32 + 13) = 2 · 32 + 2 · 13 = 64 + 26 = 90;

3) 7 · (10 + 5) = 7 · 10 + 7 · 5 = 70 + 35 = 105.

Источник

Содержание:

Определение произведения чисел
Свойства произведения чисел

Определение произведения чисел

Произведение $p$ чисел
$a_{1}, a_{2}, dots, a_{n}$ есть результат умножения этих чисел: $p=a_{1} cdot a_{2} cdot ldots cdot a_{n}$ .
В частности, если умножаются два числа $a$ и $b$, то

Пример

Задание. Найти произведение чисел:

1) 1.2$cdot 3$ ; 2) 4$cdot 5 cdot 13$

Ответ.

$1,2 cdot 3=3,6$

$4 cdot 5 cdot 13=260$

Свойства произведения чисел

Коммутативность: $n cdot m=m cdot n$
Ассоциативность: $(n cdot m) cdot k=n cdot(m cdot k)$

На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.
Дистрибутивность: $(n+m) cdot k=n cdot k+m cdot k$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти произведение чисел удобным способом:

1) 5$cdot 17 cdot 2$ ; 2) 7$cdot 2 cdot 15 cdot 5$

Решение. По свойства умножения имеем:

$$5 cdot 17 cdot 2=(5 cdot 2) cdot 17=10 cdot 17=170$$

$$7 cdot 2 cdot 15 cdot 5=(7 cdot(2 cdot 15)) cdot 5=(7 cdot 30) cdot 5=210 cdot 5=1050$$

Ответ.

$5 cdot 17 cdot 2=170$

$7 cdot 2 cdot 15 cdot 5=1050$

Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие
натуральные числа или
десятичные дроби.

Пример

Задание. Найти произведение чисел

1) 156$cdot 32$ ; 2) $4,71 cdot 3,1$

Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое,
полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем
под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в
столбик

Умножение десятичных дробей во втором примере производится следующим образом: не обращая внимания на запятые, дроби
перемножаются как целые числа; в получившемся произведении отделяют справа число знаков, равное сумме чисел знаков после
запятой у сомножителей. В нашем случае в первом сомножителе два знака после запятой, во втором — один, значит, в ответе
нужно отделить справа три знака:

Ответ.

$156 cdot 32=4992$

$4,71 cdot 3,1=14,601$

Читать дальше: что такое простое число.

Источник

Определение

Произведением чисел в математике называется результат их умножения.

Пример: Найдите произведение чисел.

14×15=210

Здесь 14 и 15 называются — множители.

Свойства

1. Коммутативность.

Пример: Вычислить произведение чисел.

17×12=204 и 12×17=204

Переместительный закон: При перестановке множителей результат не меняется.

2. Ассоциативность.

Пример:

11×19×32=6688

(11×19)×32=6688

11×(19×32)=6688

Сочетательный закон: Если группу множителей заменить их произведением, результат не изменится.

3. Дистрибутивность.

Пример:

(15+12)×9=243 и 15×9+12×9=243

Распределительный закон: Умножая сумму на число, можно на это число каждое слагаемое умножить и результаты сложить.

Большие числа, а также десятичные дроби умножают в столбик.

Нет времени решать самому?

Наши эксперты помогут!

Произведение цифр числа

Пример: найти произведение цифр числа 428

4×2×8=64

Произведение суммы и разности чисел

(23+14)×(23-14)=37×9=333

Наименьшее произведение чисел

При умножении любого числа на 0, получится ноль. Наименьшее произведение чисел равно нулю.

Сумма двух произведений чисел

(7×8)+(9×3)=56+27=83

Ответ: 83

Пример: Найди сумму и произведение чисел 14 и 72

Решение:

14+72=86 — сумма

14×72=1008 — произведение

Источник

Как найти произведение суммы

Решение

Умножение числа на сумму

Примеры

Определение произведения чисел

Свойства произведения чисел

Не пропустите также: