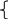Сферическая поверхность — шар
При вращении окружности вокруг ее диаметра образуется поверхность вращения, называемая сферой. Сферическая поверхность — геометрическое место точек, равноудаленных от ее центра. Сфера — единственная геометрическая поверхность, которая имеет бесконечное число осей, проходящих через ее центр, что удобно использовать при построении проекций точек на ее поверхности и при решении различных позиционных задач с геометрическими формами, в образование которых входит сфера.
Геометрическое тело, ограниченное сферой, называют шаром.
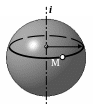
Проекции шара и проекции его очерковых окружностей
Все три очерка шара — фронтальный, горизонтальный и профильный -представляют собой окружности одного диаметра с центром в точке 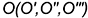
Каждая точка на поверхности шара описывает вокруг соответствующей оси окружности, называемые параллелями.
Фронтальный очерк шара — окружность 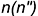
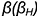
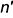
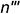
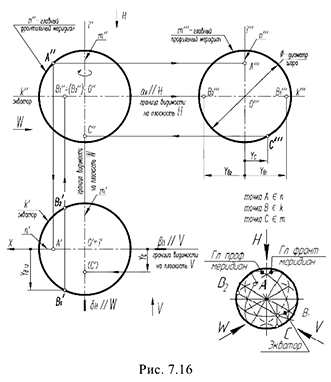
Горизонтальный очерк шара — это окружность 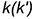
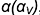
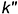
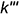
Профильный очерк шара — это окружность 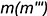
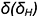
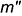
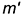
!!! Запомните характерные признаки шара на чертеже — три очерковые окружности одного диаметра.
Построение проекций точек на поверхности шара
На рис. 7.16 показаны примеры построения проекций точек, лежащих на характерных очерковых окружностях шара.
Точка 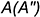
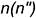
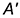
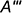
Точки 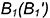
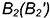
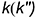
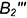
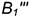
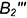
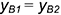
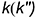
Точка 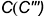
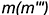
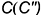
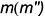
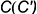
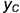
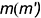
!!! Видимость проекций точки на проекциях шара определяется видимостью той части поверхности шара, на которой лежит точка, и определяется указанными границами видимости при взгляде на каждую плоскость проекций.
На рис. 7.17 показаны примеры построения проекций точек 
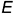
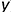
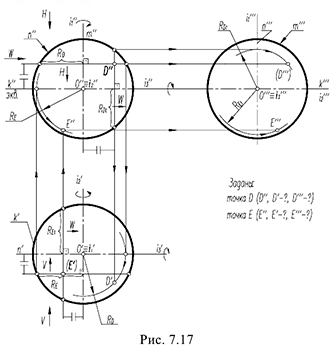
Точка 
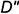
Для построения ее горизонтальной проекции 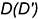
1-е действие. Провести через фронтальную проекцию точки 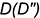
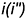
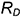

2-е действие. Провести горизонтальную проекцию этой параллели: окружность радиусом 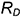
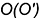
3-е действие. Построить по линии связи горизонтальную (видимую) проекцию точки 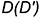
Точка 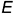
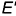
Для построения ее фронтальной проекции 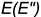
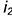
1-е действие. Провести через горизонтальную проекцию точки 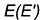
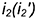
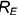
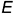
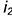
2-е действие. Провести фронтальную проекцию этой параллели: окружность радиусом 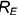
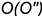
3-е действие. Построить по вертикальной линии связи фронтальную видимую проекцию точки 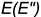
Для построения профильных проекций заданных точек 
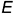
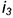
1-е действие. Провести через фронтальную проекцию точки 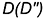
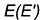
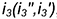
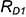
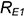

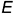
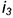
2-е действие. Провести профильные проекции этих параллелей: окружности радиусами 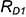
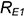
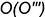
3-е действие. Построить по горизонтальным линиям связи профильные проекции точек 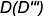
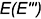
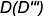
Построение проекций шара со срезами плоскостями частного положения
Всякая плоскость пересекает поверхность шара по окружностям (круговым параллелям). В зависимости от расположения секущих плоскостей относительно плоскостей проекций 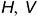
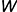
На рис. 7.18 показан пример построения проекций шара со срезами горизонтальной плоскостью 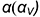
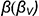
Окружность сечения шара горизонтальной плоскостью 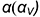
Окружность сечения шара профильной плоскостью 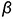
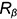
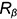
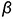
На этом же рисунке показано расположение проекции характерных точек 1,2, 3, 4, 5 и б, лежащих в плоскостях сечений на характерных очерковых окружностях шара:
Оформление очерков проекций ясно из чертежа.
На рис. 7.19 показан пример построения проекций шара со срезом фронтально-проецирующей плоскостью 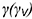
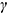
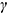
Проекции шара со срезом построены по проекциям точек, обозначенных на фронтальной проекции сечения
Горизонтальная проекция шара со срезом в виде эллипса построена по горизонтальным проекциям обозначенных точек:
-точки 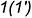
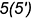
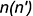
-точки 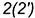
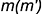
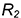
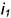
Построенные видимые горизонтальные проекции точек соединить плавной кривой эллипса с помощью лекала.
Очерк горизонтальной проекции определяет его экватор вправо от точек 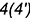
Профильная проекция шара со срезом в виде эллипса построена по профильным проекциям обозначенных точек:
Построенные видимые проекции точек соединить плавной кривой эллипса.
Очерк профильной проекции определяет профильный меридиан 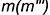
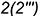
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
Точка принадлежит
поверхности сферы, если она принадлежит
линии этой поверхности.
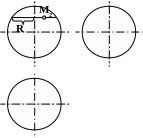
В качестве линии
берется параллель, проходящая через
данную точку. Радиус параллели R
замеряют от оси вращения до образующей
сферы (рис.57).
Рис.57
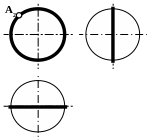
7.9 Построение проекций точки На поверхности сферы
R
1 Случай
Дано:
— сфера
А
Построить
недостающие проекции точки А.
Точка А – опорная
точка, т.к. принадлежит очерку поверхности
сферы, поэтому для построения проекций
точки не требуется дополнительных
линий.
1. Через точку М
проведите параллель.
2.
Замерьте радиус параллели.
Фронтальная
проекция точки принадлежит фронтальному
меридиану.
Спроецируйте
точку А на горизонтальную и профильную
проекции фронтального меридиана (А1,
А3).
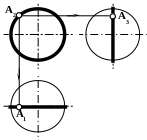
2 Случай
Дано:
— сфера
M
Построить
недостающие проекции точки M.
M2
1. Через точку М
проведите параллель.
2. Замерьте радиус
параллели.
3. На горизонтальной
проекции сферы проведите окружность
радиусом R.
Это будет горизонтальная проекция
параллели.
4. Спроецируйте
точку М на горизонтальную проекцию
параллели. Получится две проекции М1,
М1I
M2
М1
М1I
М3
М3I
5. Для того, чтобы
получить профильную проекцию точки М3
необходимо замерить расстояние от оси
Х до проекции М1
на горизонтальной проекции сферы и
отложить это расстояние от оси Z
вправо на профильной проекции сферы
(показано фигурными скобками).
6. Аналогично
постройте проекцию М3I.
7.10 Поверхность тора
Тор образуется
вращением окружности l,
вокруг оси i,
не проходящей через ее центр.
На (рис.58)
представлен открытый
тор, так
как ось вращения не пересекает эту
окружность.
Рис.58
Рис.59
Если ось вращения
тора перпендикулярна горизонтальной
плоскости проекций, то проекция тора
на эту плоскость изображается двумя
концентрическими окружностями (рис.59).
Радиус малой
окружности (рис.57) равен расстоянию от
оси вращения до точки 1.
Радиус большой
окружности равен расстоянию от оси
вращения до точки 2.
На фронтальной
плоскости проекций тор изображается
двумя образующими окружностями,
соединенными сверху и снизу прямыми
линиями. Половины окружностей будут
не видны.
Тор называется
закрытым
(рис.60), если ось вращения пересекает
или касается окружности.
Рис.60
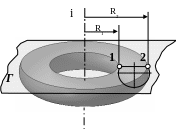
Если через
поверхность тора провести секущую
плоскость Г, перпендикулярно оси
вращения, то в сечении получатся две
окружности – параллели (рис.61). Радиус
меньшей параллели R1
замеряют от оси вращения до точки 1
образующей окружности. Радиус большой
параллели равен расстоянию от оси
вращения до точки 2 образующей окружности.
Рис.61
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ниже приведены некоторые примеры построений в прямоугольных изометрической и диметрической проекциях.
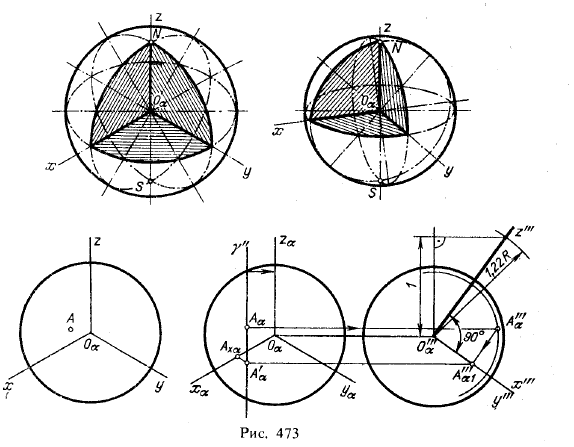
I. Проекция сферы. На рис. 473 сверху дано изображение сферы в изометрической и диметрической проекциях.
В обоих случаях сфера показана с вырезом одной восьмой части.
Окружности, представляющие собой очерк проекции, проведены: для
изометрической проекции радиусом, равным
1,22R, для диметрической проекции радиусом 1,06R, где R — радиус
сферы. Эллипсы в обоих случаях соответствуют экваториальному и двум
меридиональным сечениям.
На рис, 473 внизу слева дано изображение сферы в изометрической
проекции; на видимой стороне сферы дана точка А. Справа показано
построение вторичной проекции А’α (см, рис, 449) и трехзвенной
координатной ломаной линии АαА’αАхαОα, что дает возможность определить прямоугольные координаты точки А в
пространстве. Построение выполнено в предположении, что плоскость
изометрических проекций занимает фронтальное положение и что
равнонаклоненнью к ней оси х, у, z прямоугольных координат спроецированы
не только на эту плоскость, но и на дополнительную профильную плоскость
π3. Получается система плоскостей проекций α, π3
и проекции Аα и А'»α заданной точки А, причем А'»α получена при помощи сечения сферы пл. γ. Вторичная проекция точки А также изображена двумя проекциями: А'»α1 и А’α
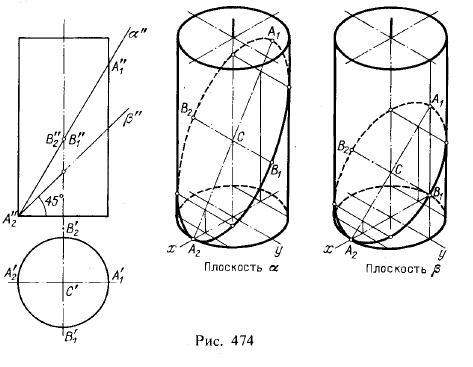
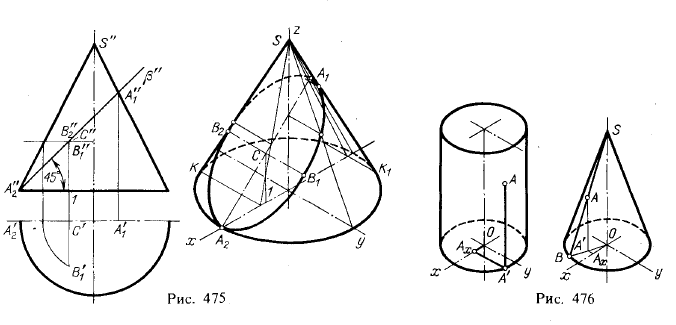
2. Линии пересечения цилиндра и конуса плоскостью. На рис, 474 и 475
показано построение в изометрической проекции линий пересечения цилиндра
и конуса фронтально-проецирующими плоскостями 1). В рассматриваемых случаях линии пересечения представляют собой эллипсы.
Прежде всего, руководствуясь чертежом, наносим по координатам точек А1 и А2 линии наклона ллоскостей α и β. Для построения точек эллипсов берем вспомогательные секущие плоскости: для цилиндра — параллельно его
образующим и плоскости yOz, для конуса — про-
1) Построение выполнено в приведенных коэффициентах искажения.
ходящие через его вершину параллельно оси у. Эти плоскости задаются
их следами, параллельными оси у, на плоскостях оснований цилиндра и
конуса.
При таком выборе вспомогательных плоскостей прямые, по которым они
пересекаются с плоскостями α и β, получаются параллельными оси γ. В
пересечении этих прямых с образующими цилиндра и конуса получаются точки
эллипса.
В первую очередь следует найти такие характерные точки, как отмеченные на чертежах буквами А1, А2. В1 и В2,
а также получаемые на очерковых линиях изометрической проекции. Малая
полуось получаемого в сечении эллипса, равная С’В’1, сохраняет свою
величину и в изометрической проекции (С’В’1 = СВ1). Но свое значение
малой оси для эллипса в изометрической проекции отрезок В1В2 сохраняет лишь при пл. β, т. е. при указанном на рисунке угле наклона этой плоскости, равном 45°.
Действительно, в этом случае отрезок В1В2 будучи параллельным оси у, остается и в изометрической проекции перпендикулярным к A1A2, следовательно, отрезки A1A2 и В1В2 сохраняют свое значение осей эллипса. В случае же иного наклона плоскости, как это показано на цилиндре для пл. α, отрезки А1А2 и В1В2 в изометрической проекции не являются осями эллипса, а лишь его сопряженными диаметрами.
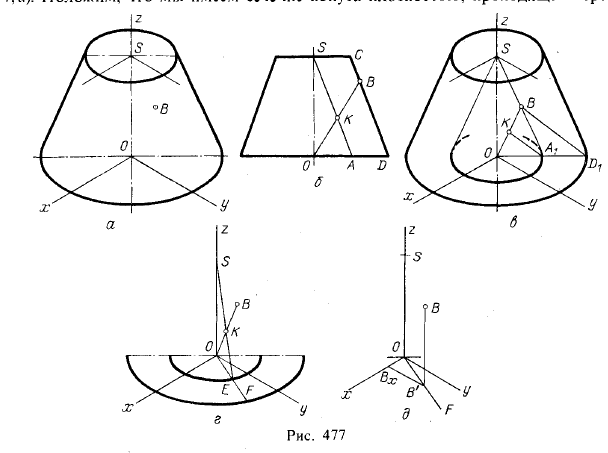
3. Построение координатных отрезков для точки, заданной на
поверхности цилиндра и конуса вращения в аксонометрической проекции. На
рис. 476 даны примеры для цилиндра и конуса в изометрической проекции.
Во всех случаях начало координат взято в центре основания (точка О).
Через заданную на цилиндре точку А проведена прямая параллельно оси
z, и из вторичной проекции А’ проведена прямая шраллельно оси γ до
пересечения с осью х. Отрезки 0Аx, АxА’ и А’А позволяют определить координаты точки А в данной системе осей координат.
Через заданную на конусе точку А проведена образующая и построена
вторичная проекция (ОВ) этой образующей. Проводя из точки А
перпендикуляр до пересечения с ОВ, получаем вторичную проекцию точки А.
Дальнейшее ясно из чертежа.
На рис. 477 показано построение координатных отрезков для точки,
заданной на поверхности усеченного конуса вращения в изометрической
проекции (рис. 411, а). Положим, что мы имеем сечение конуса плоскостью,
проходящей через ось
конуса и точку В (рис. 477,6). В полученной трапеции проведена прямая
SA || CD и пересекающая ее в точке К прямая ОВ. Получаем OK : KB = OA : AD. Но эта пропорция сохранится в изометрической проекции. Построим
конус с вершиной в точке S и с образующей, параллельной образующей
усеченного конуса (рис. 477, в). От
ношение OA1: A1D1 повторяет
отношение OA : AD, содержащееся в указанной выше пропорции. Теперь можно
получить точку К на ОВ на рис. 477, в. Образующая, проведенная через
точки S и Е, определяет точку К (рис. 477, г) и проекцию OF образующей,
на которой находится точка В. Отсюда мы получаем возможность получить
вторичную проекцию В’ (рис. 477, д) и координатные отрезки ВВ’, В’Вx и ОВх, определяющие координаты z, у и х.
Указанное построение дается на случай, если нельзя достроить
усеченный конус до полного. Если достроить можно, то построение
производится, как показано для конуса на рис. 477,6.
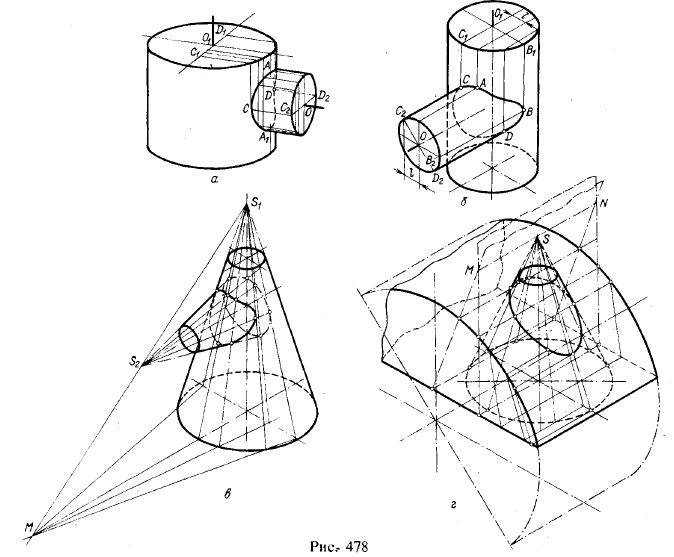
4. Примеры построения линий пересечения цилиндрических и конических
поверхностей вращения между собой. Линии пересечения строят по точкам;
эти точки находят или по их координатам, взятым с ортогональных
проекций, или способом вспомогательных секущих плоскостей
непосредственно в аксонометрических проекциях. Последнее показано на
рис. 478, а — г.
Вспомогательные секущие плоскости пересекают данные цилиндры и конусы
по образующим линиям. На рис; 478, а оси цилиндров пересекаются, на
рис. б) скрещиваются. Если на рис. а) точки А и А1 определялись при помощи секущей плоскости, проходящей через оси обоих цилиндров, то на рис. б) надо учесть смещение на
l 1). На рис. 478,в секущие плоскости проходят через прямую S1S2, а их следы на плоскости основания конуса с вершиной S1 проходят через след прямой S1S2 на этой плоскости. На рис. 478, г плоскости проходят через прямую MN, проведенную через вершину конуса — точку S — параллельно образующей цилиндра.
1) Разметка точек буквами произведена лишь для пояснении.
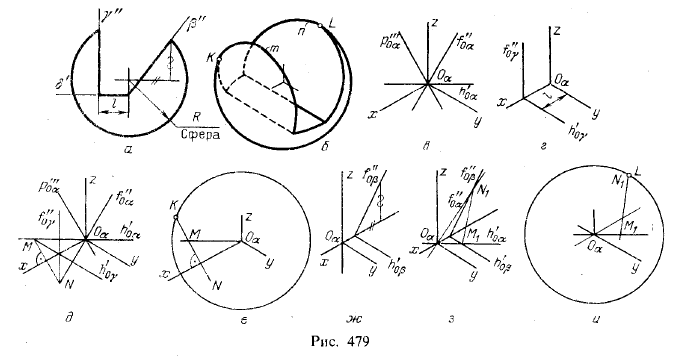
5. Построение точек касания окружности — очерка проекции сферы — с
эллипсом — проекцией окружности, получаемой на сфере при пересечении ее
плоскостью. На рис. 479, а показана сфера, срезанная тремя плоскостями — профильной
(γ), горизонтальной (δ) и фронтально-проецирующей (β). По этому чертежу
построена: изометрическая проекция (рис. 479,6) в приведенных
коэффициентах искажения. Эллипс m построен так, как было показано на
рис. 469, а эллипс n — как на рис. 465. Проекция сферы дана очерком —
окружностью радиуса равного 1,22R. Эта окружность касается эллипса m в
точке К, эллипса n — в точке L.
Рассмотрим, как найдена точка К. Она получена на окружности — очерке
проекции сферы, т. е. в плоскости изометрической проекции (α), и в то же
время на эллипсе m т. е. в пл. γ, пересекающей сферу. Но если точка
принадлежит одновременно двум плоскостям, то она принадлежит линии
пересечения этих плоскостей.
Плоскость изометрической проекции, как известно, равнонаклонна к π1, π2 и π3. Треугольник следов этой плоскости равносторонний (см. рис. 457). Отнеся пл. α к точке Оα, т. е. к началу осей и центру сферы, помучим положение следов, указанное на рис. 479, в.
Пл. γ в системе тех же осей изобразится в следах, как показано на
рис. 479,г. Совместим рис. в) и г) и построим линию пересечения
плоскостей α и γ (рис. 479, е): прямая MN проходит через точку M
пересечения горизонтальных следов параллельно следу р»‘0α, так как γ||π3 (при этом р»‘0α⊥OαX. следовательно, MN⊥Оαх).
Теперь остается найти точку К в пересечении прямой MN с окружностью — изометрической проекцией сферы (рис. 479, е).
Для определения положения точки L (см. рис. 479, б) надо изобразить в
системе изометрических осей фронтально-проецирующую пл. β (рис. 479,.ж),
а затем найти прямую пересечения плоскостей α и β (рис. 479, з), эта
прямая проходит через точку M1 пересечения следов h’0β и h’0α и через точку N1 пересечения следов f»0β и f»0α. Искомая точка L получается в пересечении прямой M1N1 с окружностью — изометрической проекцией сферы (рис. 479, и).
Время на прочтение
2 мин
Количество просмотров 17K
Мне очень понравился разбор задачи от 3Blue1Brown, выкладываю конспект для тех, кто любит изящные решения математических задач в читабельном виде.
Математическая олимпиада им. Уильяма Лоуэлла Патнема (William Lowell Putnam Mathematical Competition) — математическая олимпиада для студентов бакалавриата, обучающихся в университетах (колледжах) США и Канады. Вдохновителем олимпиады был Уильям Лоуэлл Патнем, американский юрист и банкир. Проводится Математической ассоциацией Америки ежегодно с 1938 года. Денежными призами награждаются пять лучших университетских команд (приз $25 000 за первое место) и двадцать пять студентов, лучших в личном зачете (приз $1000 за первое место).
— Википедия
Длится олимпиада два раза по 3 часа, всего 12 задач по 10 баллов за каждую. Средний балл, который набирают студенты — 1 или 2. Рассмотрим одну из самых сложных задач из этой олимпиады.
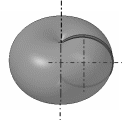
Выберем 4 случайные точки на сфере. Какова вероятность что центр сферы будет внутри тетраэдра, образованного этими точками?
Рассмотрим двумерный вариант этой задачи.
Рассмотрим 3 случайные точки на окружности. Какова вероятность, что центр окружности будет внутри треугольника?
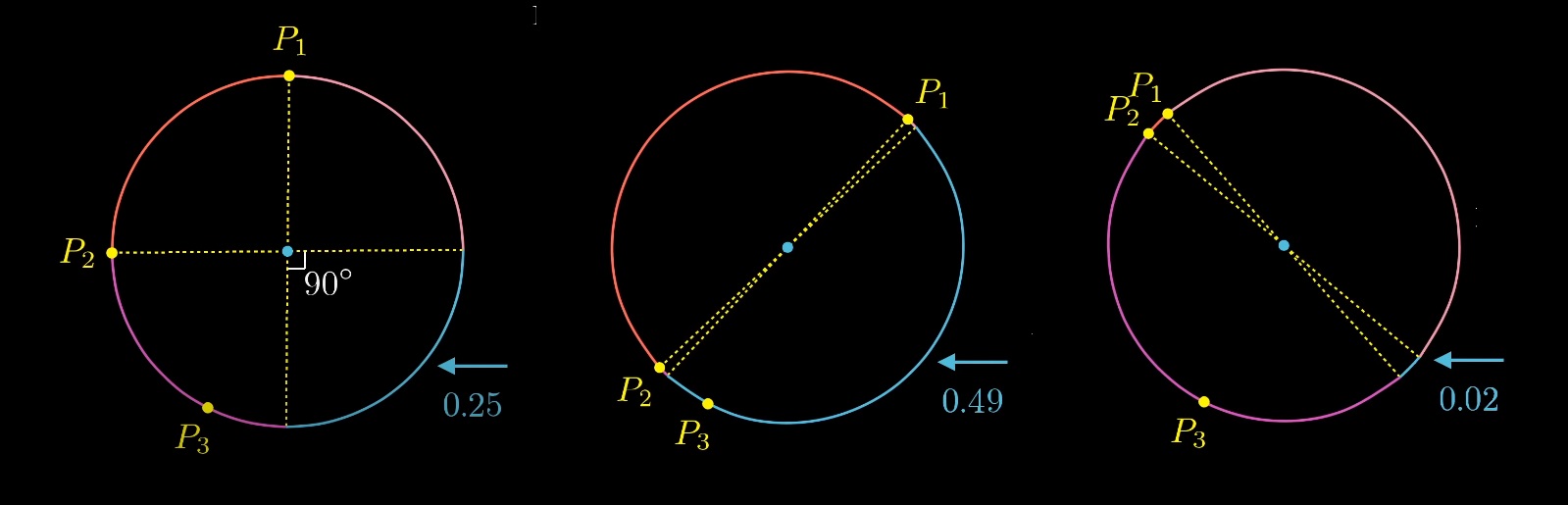
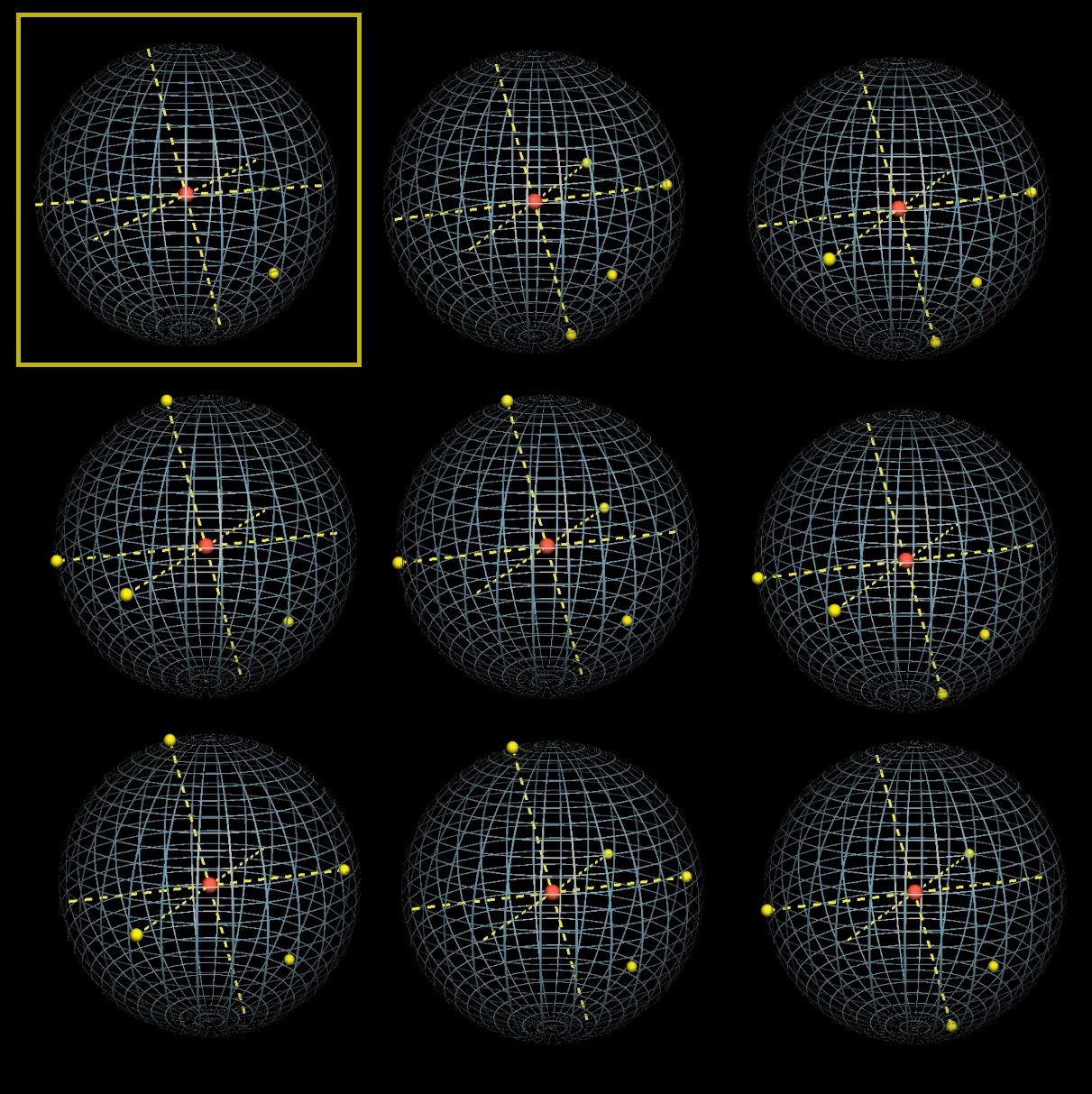
Можно закрепить две точки и поиграться с третьей. Легко заметить, что есть определенная зона, проекции закрепленных точек относительно центра, внутрь которой должна попасть третья точка, чтобы выполнилось условие. Окружность тем самым разделяется на 4 части. Вероятность попадания третей точки в дугу, равна отношению длины дуги к длине окружности. Какова длина дуги?
Вероятность колеблется от 0 до 0,5 в зависимости от расположения первых двух точек.
Какова средняя вероятность?
Зафиксируем первую точку и поиграемся со второй. Вероятность будет меняться от 0 до 0,5, то есть средняя вероятность будет 0,25.
Решение задачи для окружности и трёх точек — 25%.
Можно ли перенести такой подход на сферу и 4 точки?
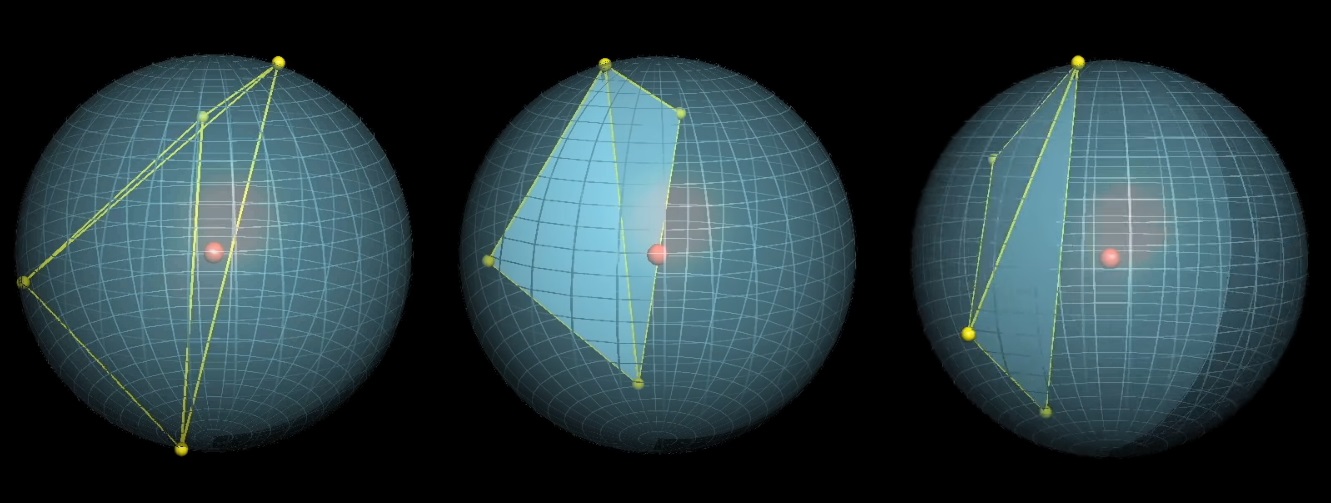
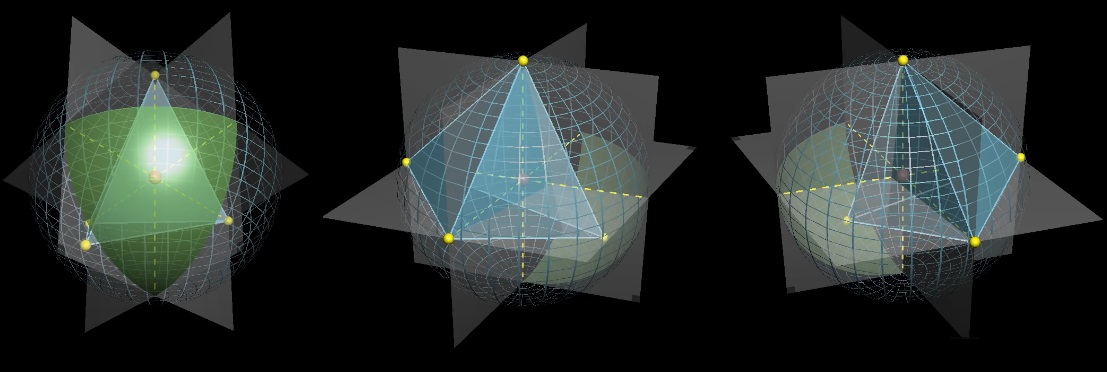
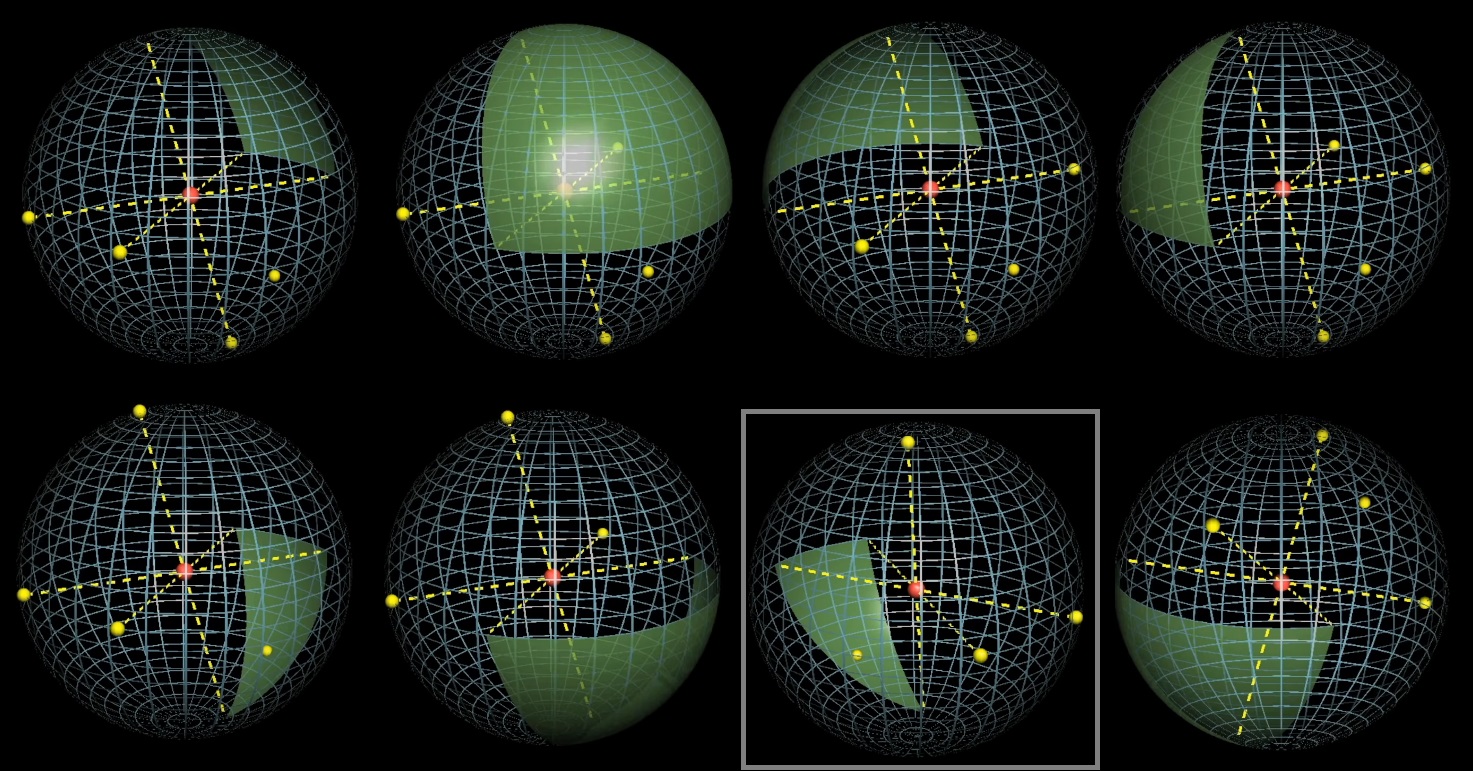
Фиксируем три точки и играем с четвертой. Нарисуем проекции фиксированных точек относительно центра и плоскостями разделим сферу на 8 частей.
Центр сферы будет находиться внутри тетраэдра, если четвертая точка попадает на зеленый сферический треугольник, который находится «напротив» зафиксированных точек относительно центра. Каков средний размер зеленой секции?
//Дальше не придумали, импровизируй.
Можно вернуться к двумерному случаю и подумать откуда взялась 1/4. Откуда 4?
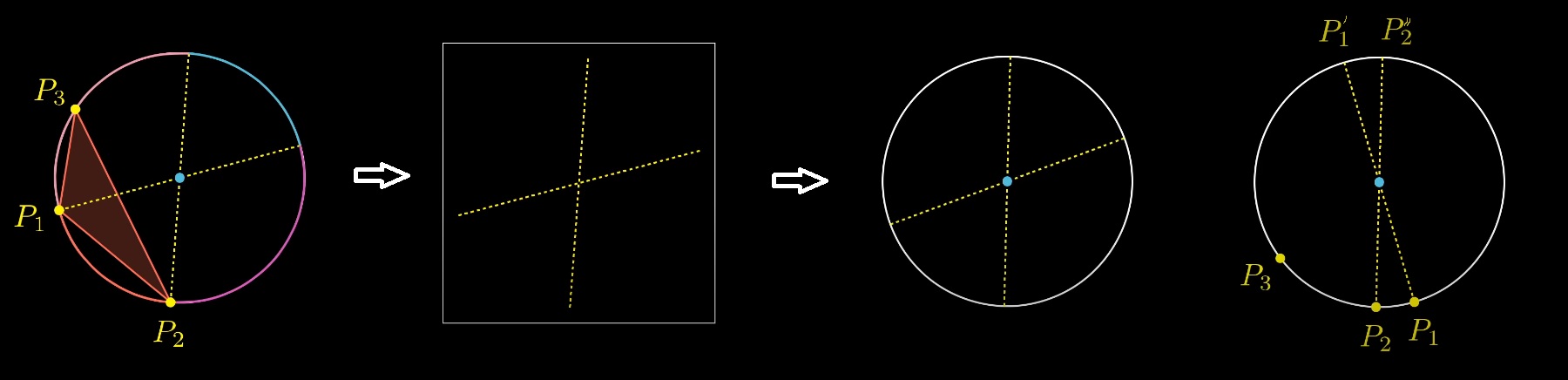
Можно перейти от 3 случайных точек на окружности к другой задаче. Выберем два случайных диаметра. Потом для каждого диаметра бросим монетку, выбирая тем самым, где будет точка Pi, с какого конца диаметра. Потом случайно выберем третью точку на окружности.
А потом еще хитрый ход.
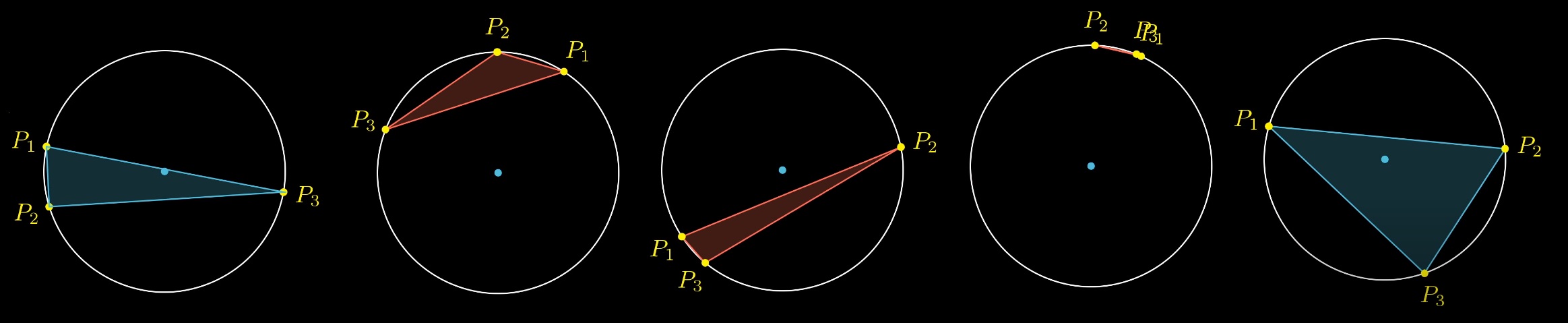
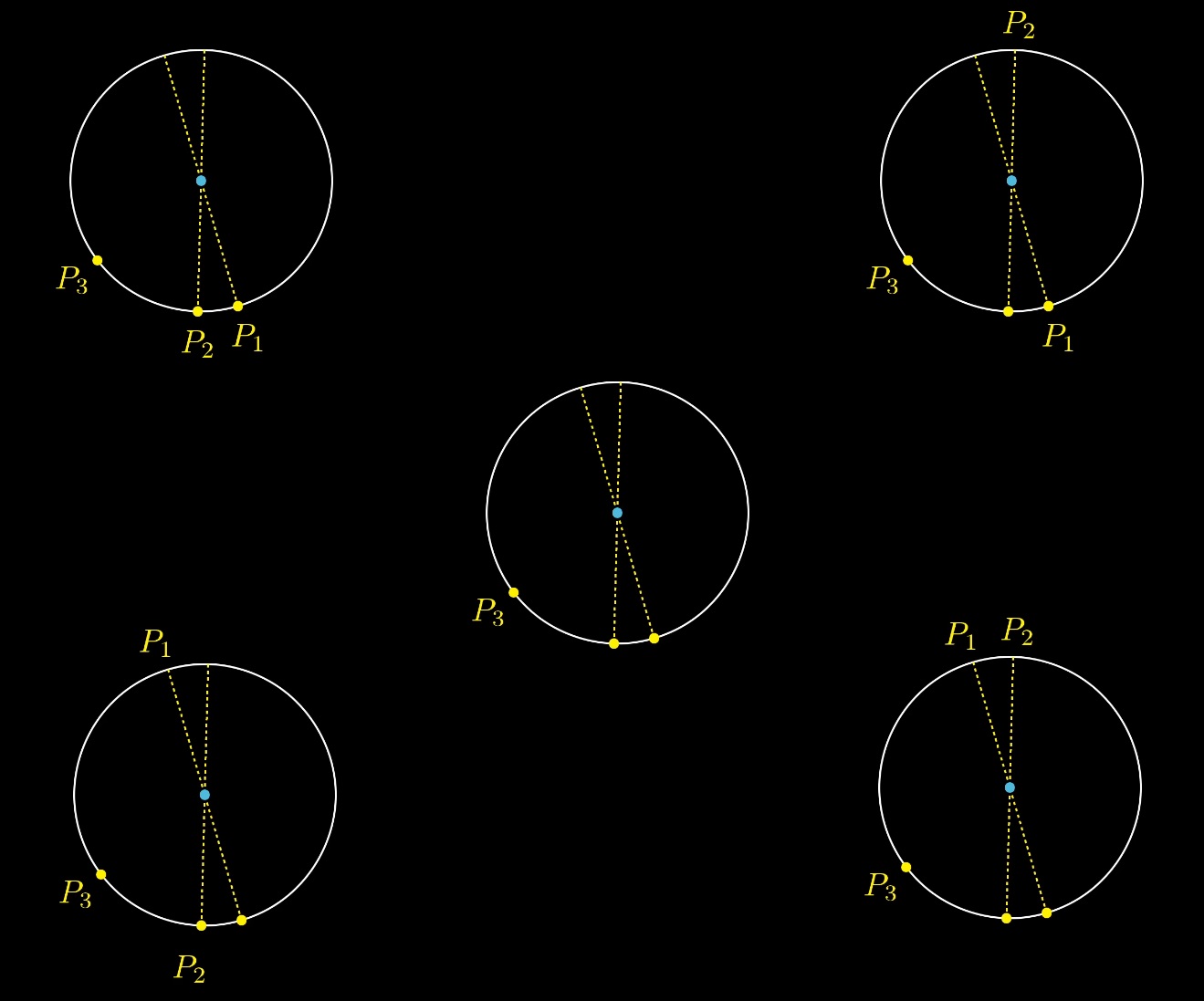
Давайте сначала выберем случайным образом третью точку, а потом случайно выберем два диаметра. У нас будет 4 варианта размещения точек P2 P1:
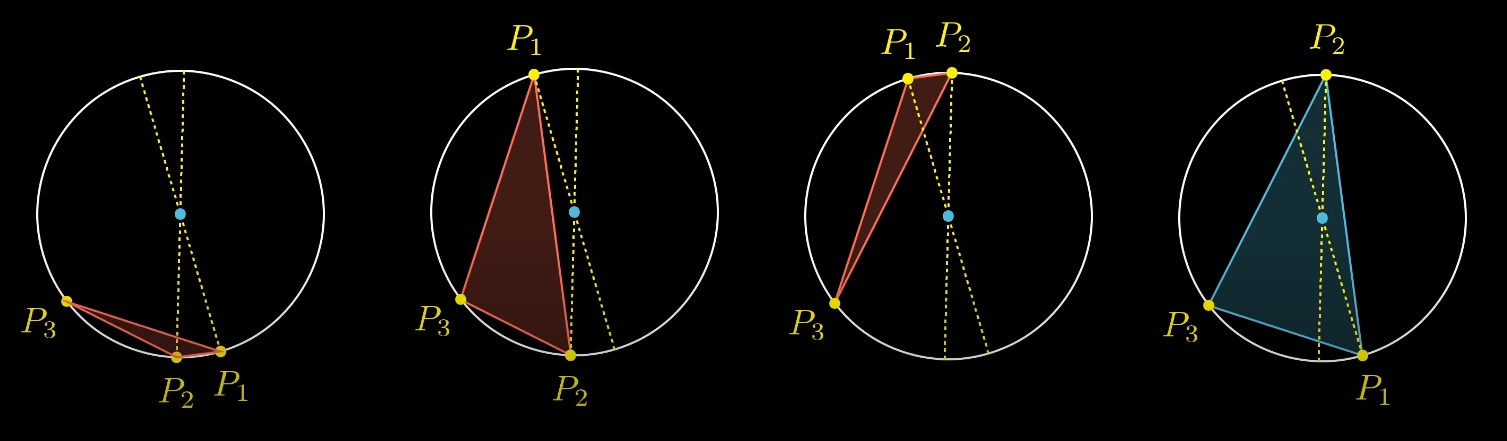
Но только один из этих 4 вариантов содержит решение, когда центр окружности внутри треугольника:
Какую бы мы ни выбирали рандомную начальную позицию третей точки и двух диаметров, только один из вариантов содержит центр окружности внутри треугольника:
То как мы переформулировали задачу:
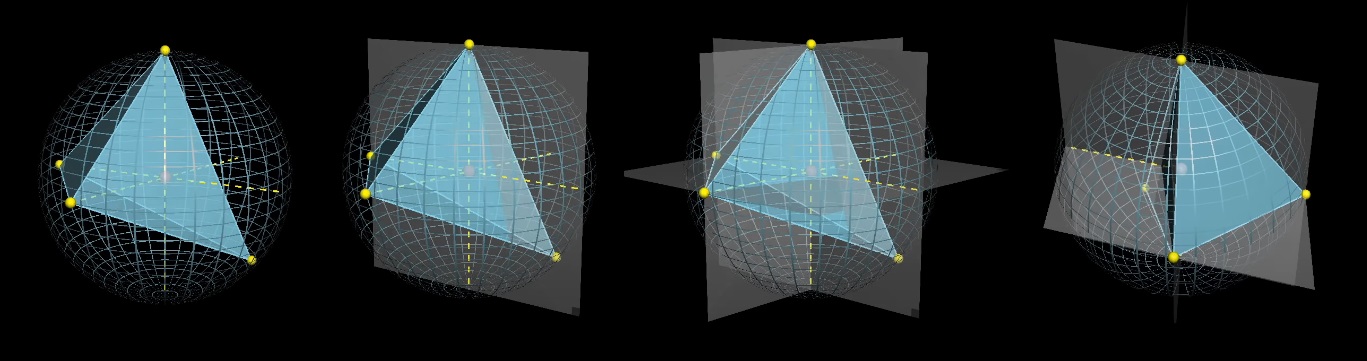
Со сферой получается 8 вариантов выбора точек, после того, как зафиксирована первая точка и выбраны три диаметра:
Только 1 из 8 удовлетворяет условию, что центр сферы внутри тетраэдра:
Ответ: 1/8
- Хардкорная линейная алгебра здесь: Capturing the Origin with Random Points: Generalizations of a Putnam Problem
- Все задачи олимпиады 1992 года: The 53rd William Lowell Putnam Mathematical Competition
Saturday, December 5, 1992
Проекции точек на поверхностях геометрических тел
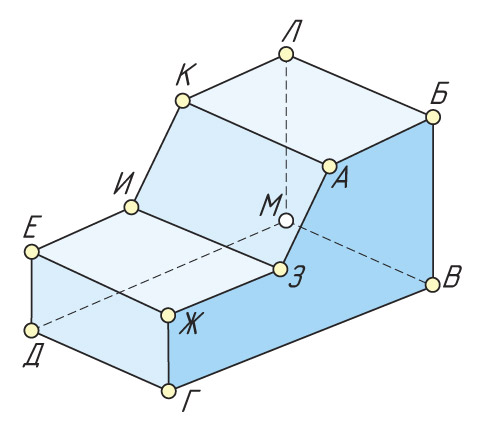
Вы уже знаете, как построить проекции предмета или объекта. Часто при изготовлении изделий необходимо по заданным проекциям определить геометрическую форму предметов и их частей. Предмет можно рассматривать как комбинацию различных геометрических элементов: вершин, ребер, граней и т. д.
Укажите количество вершин, ребер и граней изображенного предмета.
|
Для точного построения изображений ряда деталей необходимо уметь находить проекции отдельных точек. Чтобы построить проекции точки, принадлежащей поверхности геометрического тела, необходимо понять, на какой поверхности или на каком элементе поверхности (ребре, вершине, грани) находится эта точка. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки. |
 |
|
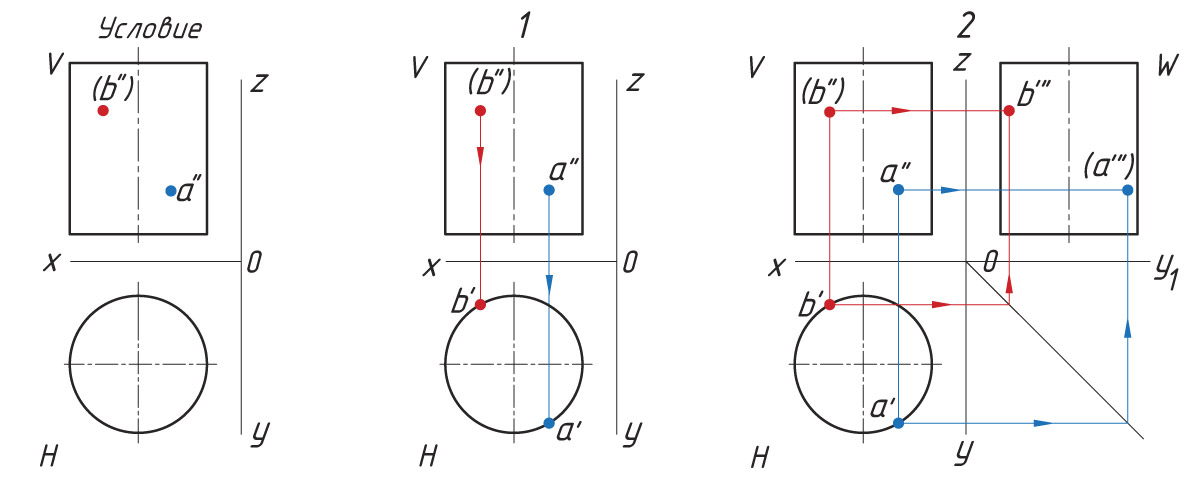
Рассмотрим проекции точки на геометрических телах. Проецирование точек на поверхности цилиндра Последовательность проецирования точек 1. Находят горизонтальные проекции точек а′ и b′. Так как горизонтальная проекция боковой проекции цилиндра отображается в виде круга, то проекции точек а′ и b′ будут находиться на нем. Для их нахождения проводят вертикальные линии связи из проекций точек а″ и b″ до пересечения с окружностью. 2. Проекции точек а′″ и b′″ находят на пересечении линий проекционной связи. |
 |
Направление взгляда на плоскости проекций H, W помогает определить видимость проекций точек на горизонтальной и профильной плоскости проекций. Например, проекции а′ и b′ на плоскости H видны. Проекция а′″ на плоскости W не видна (показана в скобках), проекция b′″ видна (показана без скобок).
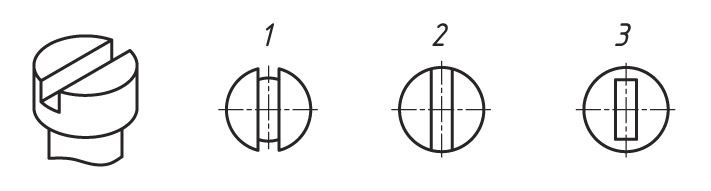
Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта.
|
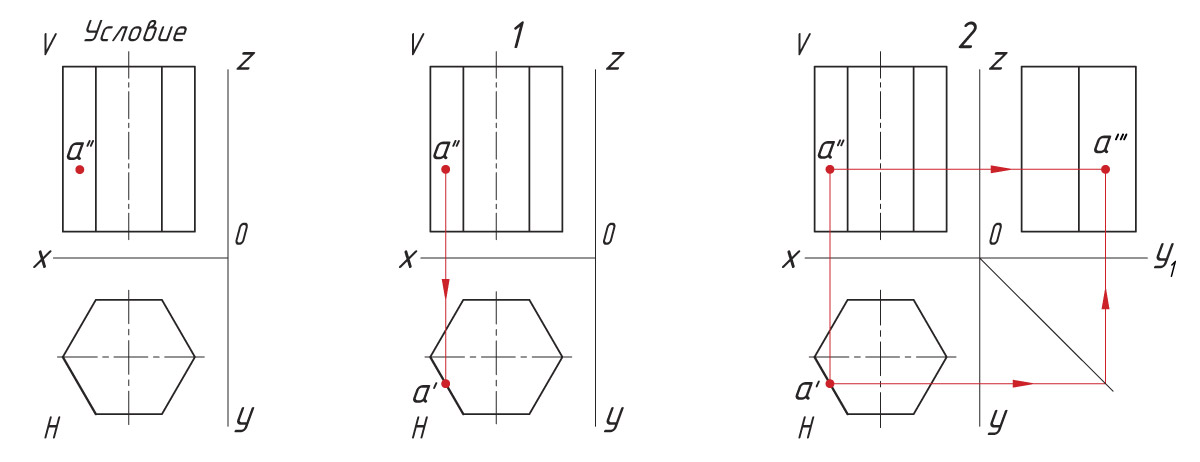
Проецирование точек на поверхности призмы Последовательность проецирования точек 1. Находят горизонтальную проекцию точки а′. Для ее нахождения проводят вертикальную линию связи из проекции точки а″ до пересечения с шестиугольником (горизонтальная проекция призмы). 2. Проекцию точки а′″ находят на пересечении линий проекционной связи. |
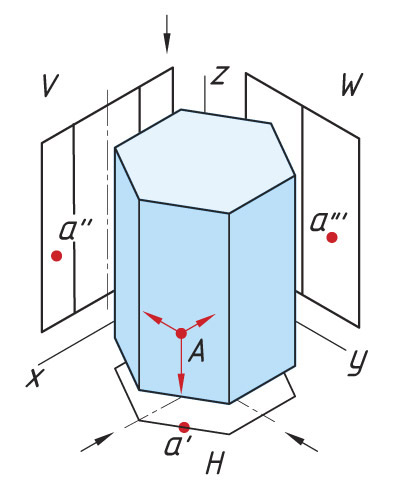 |
Опишите последовательность проецирования точки, находящейся на ребре призмы. Выполните это построение.
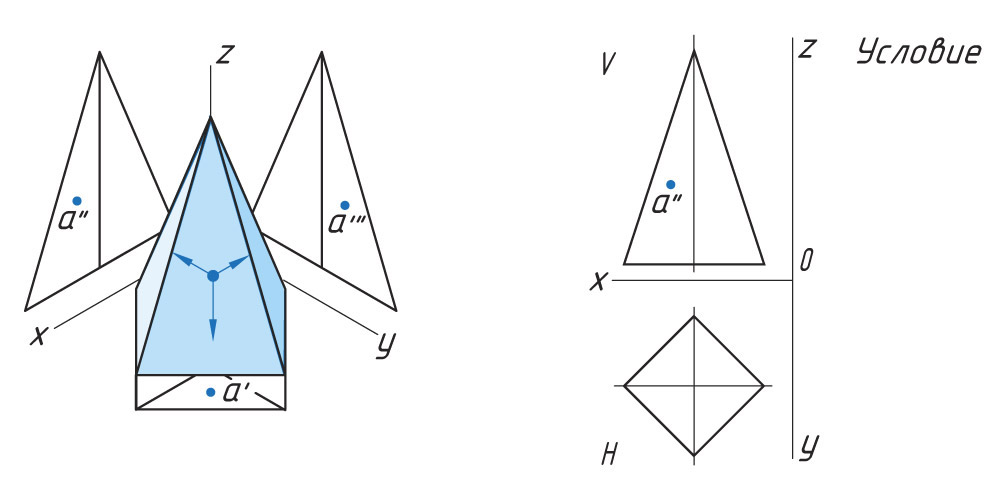
Проецирование точек на поверхности пирамиды
Построение проекции точки, лежащей на ребре
Если точка находится на ребре предмета, то сначала необходимо выполнить проекцию ребра, а затем при помощи линий проекционной связи найти проекции точки, лежащей на ребре.
Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.
Общий метод определения точки, лежащей на поверхности геометрического тела, заключается в следующем: через точку на поверхности проводят вспомогательную прямую, проекции которой легко определяются на данной поверхности.
Построение проекции точки, лежащей на грани
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности четырехгранной пирамиды.
Проекции точек можно определить несколькими способами. Рассмотрим каждый из них.
|
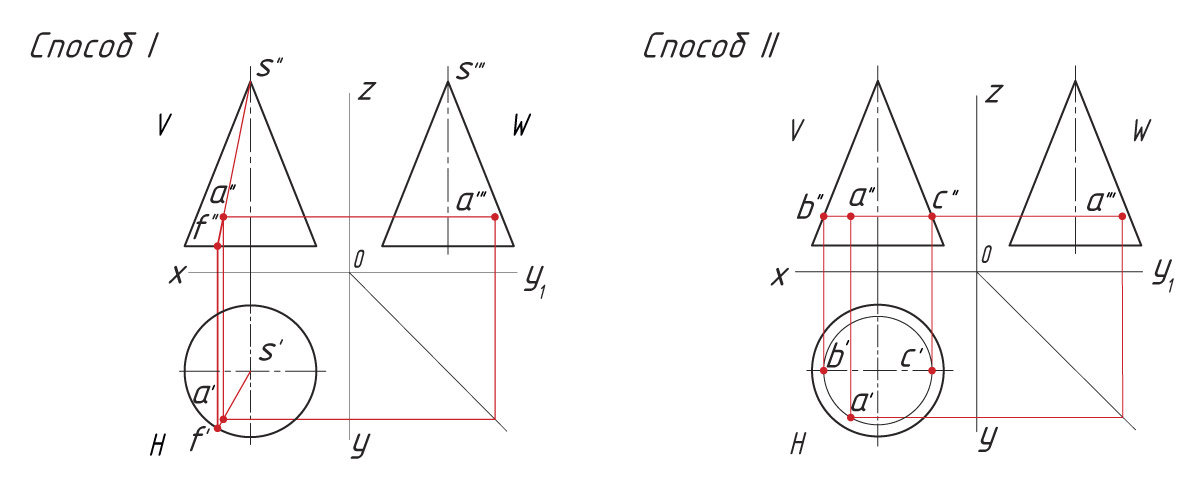
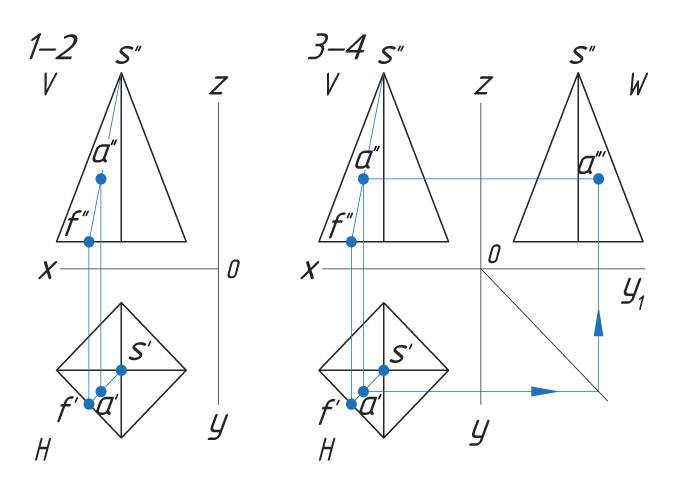
Способ I. 1. Находят горизонтальную проекцию точки а′: вспомогательной прямой соединяют заданную проекцию точки а″ с проекцией вершины пирамиды s″ и продлевают ее до пересечения с основанием в точке f″. |
 |
|
Способ II. 1. Через проекцию а″ точки А проводят вспомогательную прямую и получают точки пересечения с ребрами пирамиды 1″ и 2″. |
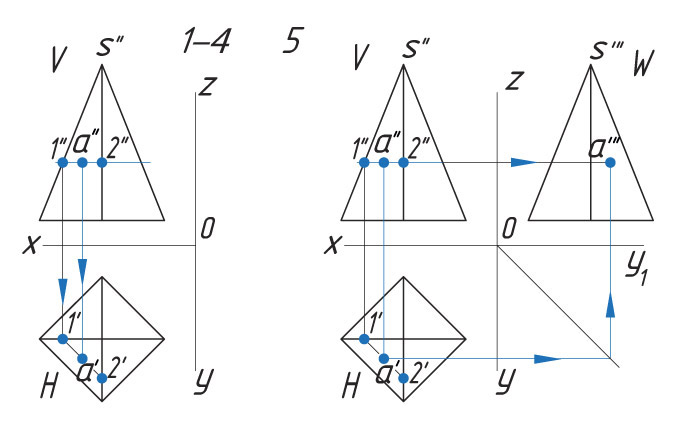 |
На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?
|
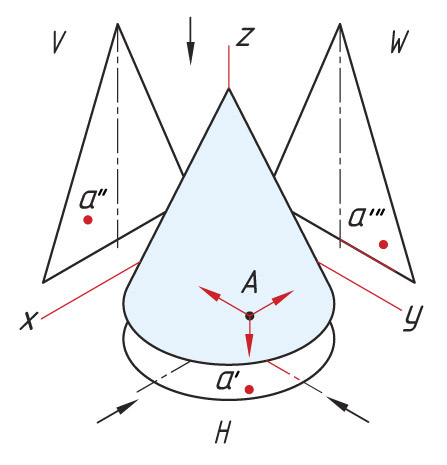
Проецирование точек на поверхности конуса. На поверхности конуса проекции точек можно также определить двумя способами. Способ I заключается в определении проекций точки с помощью вспомогательной линии — образующей, расположенной на поверхности конуса и проведенной через точку А. |
 |