Как найти проекции точек на детали - Avtoru.top - решение различных проблем

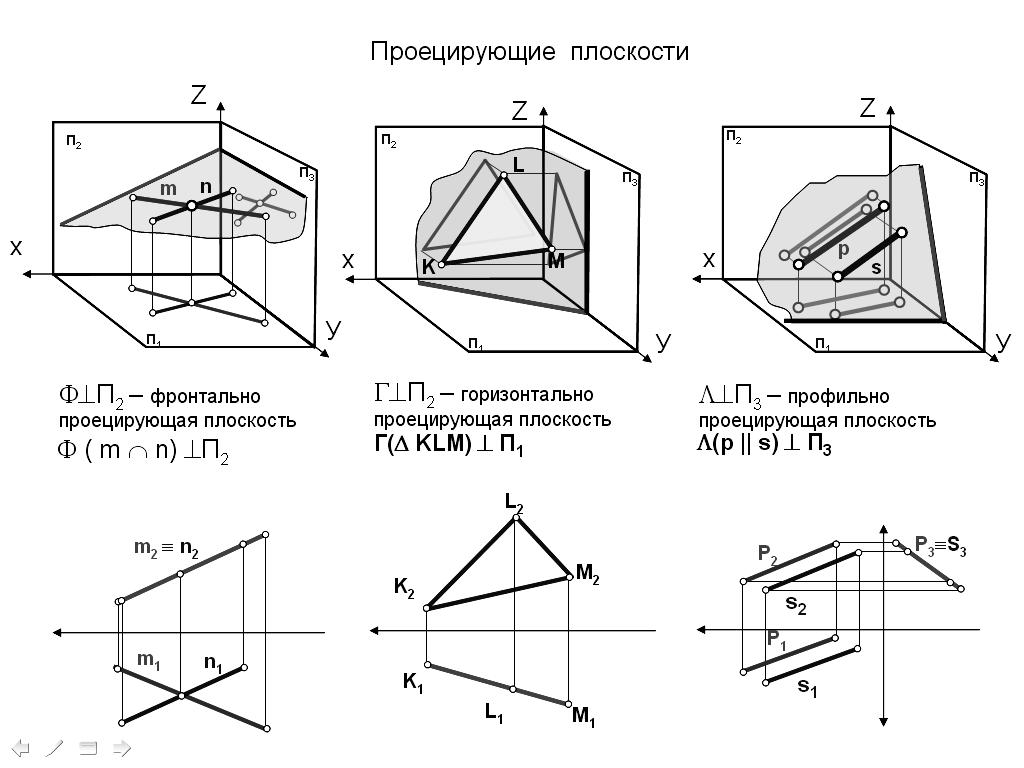
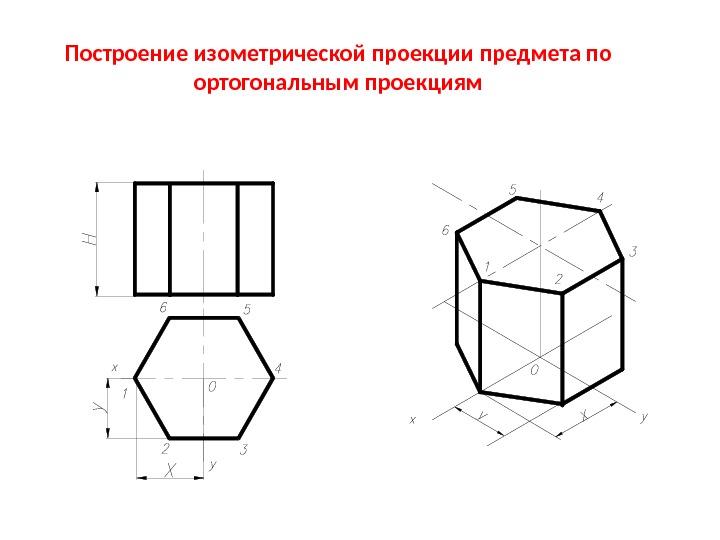
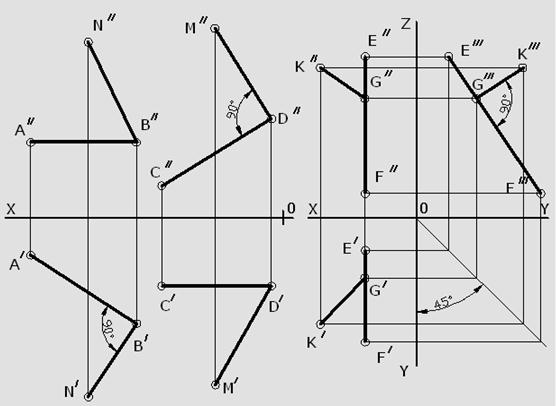
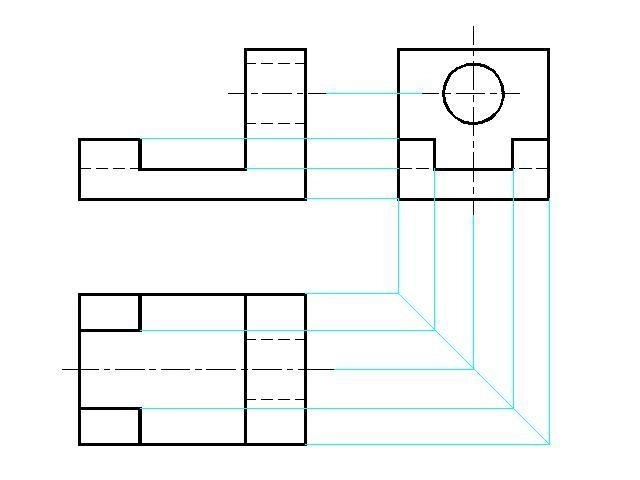
Проекции точек на поверхностях геометрических тел

Вы уже знаете, как построить проекции предмета или объекта. Часто при изготовлении изделий необходимо по заданным проекциям определить геометрическую форму предметов и их частей. Предмет можно рассматривать как комбинацию различных геометрических элементов: вершин, ребер, граней и т. д.

Укажите количество вершин, ребер и граней изображенного предмета.

Для точного построения изображений ряда деталей необходимо уметь находить проекции отдельных точек. Чтобы построить проекции точки, принадлежащей поверхности геометрического тела, необходимо понять, на какой поверхности или на каком элементе поверхности (ребре, вершине, грани) находится эта точка. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки.

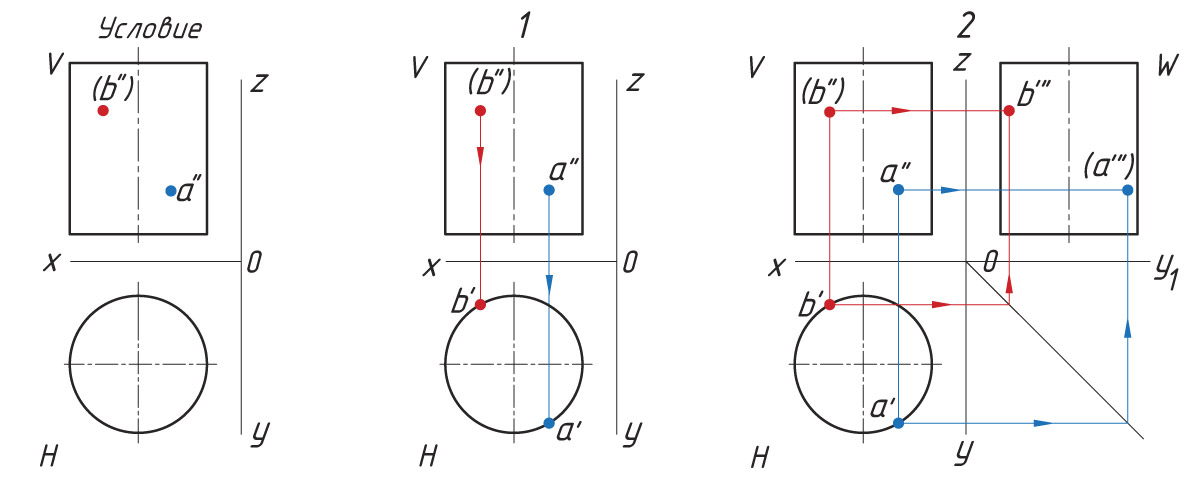
Рассмотрим проекции точки на геометрических телах.

Проецирование точек на поверхности цилиндра

Последовательность проецирования точек
Заданы фронтальные проекции а″ и b″ точек А и В, лежащие на боковой поверхности цилиндра. Проекция а″ находится на видимой части поверхности цилиндра (на плоскости V показана без скобок), b″ находится на невидимой части поверхности цилиндра (на плоскости V показана в скобках).

1. Находят горизонтальные проекции точек а′ и b′. Так как горизонтальная проекция боковой проекции цилиндра отображается в виде круга, то проекции точек а′ и b′ будут находиться на нем. Для их нахождения проводят вертикальные линии связи из проекций точек а″ и b″ до пересечения с окружностью.

2. Проекции точек а′″ и b′″ находят на пересечении линий проекционной связи.

Направление взгляда на плоскости проекций H, W помогает определить видимость проекций точек на горизонтальной и профильной плоскости проекций. Например, проекции а′ и b′ на плоскости H видны. Проекция а′″ на плоскости W не видна (показана в скобках), проекция b′″ видна (показана без скобок).

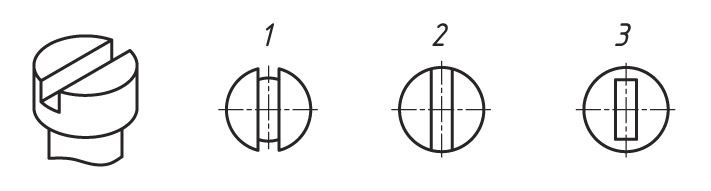
Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта.

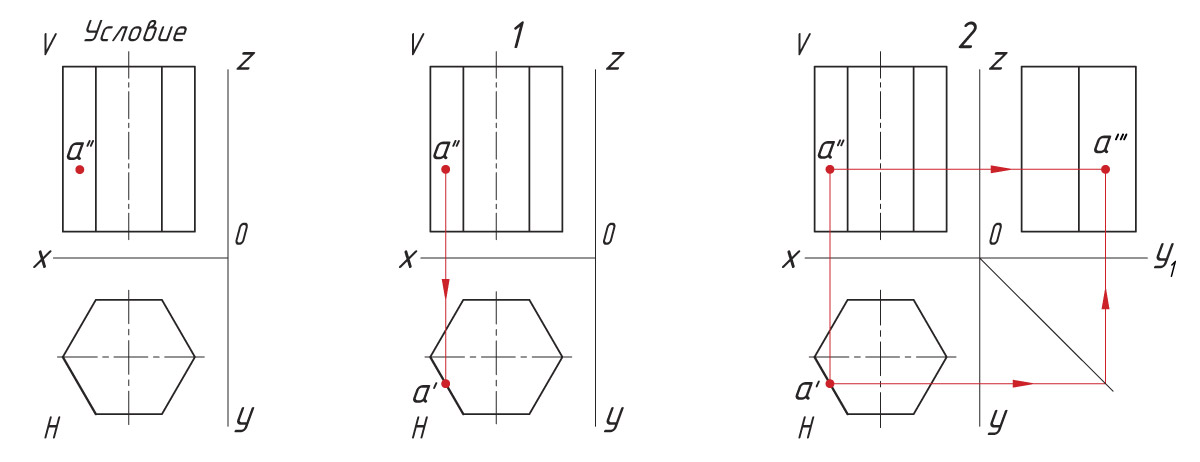
Проецирование точек на поверхности призмы

Последовательность проецирования точек
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности шестигранной призмы.

1. Находят горизонтальную проекцию точки а′. Для ее нахождения проводят вертикальную линию связи из проекции точки а″ до пересечения с шестиугольником (горизонтальная проекция призмы).

2. Проекцию точки а′″ находят на пересечении линий проекционной связи.

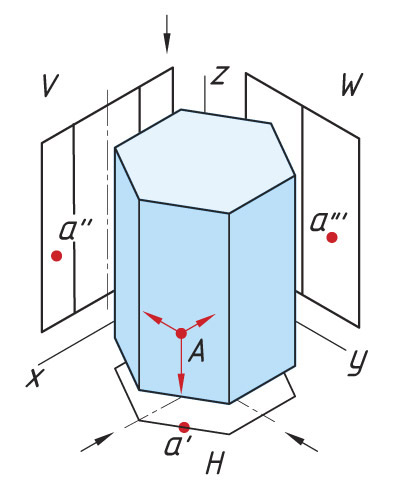Опишите последовательность проецирования точки, находящейся на ребре призмы. Выполните это построение.

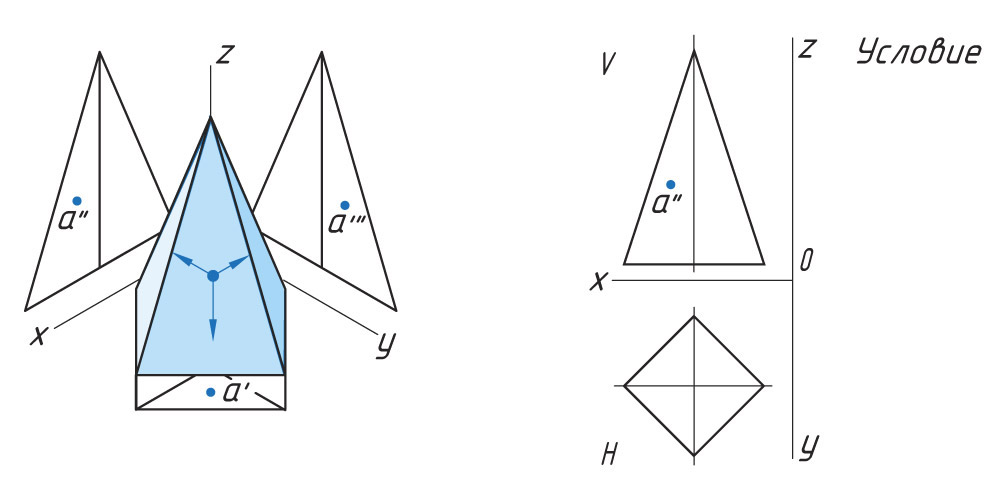
Проецирование точек на поверхности пирамиды

Построение проекции точки, лежащей на ребре
Если точка находится на ребре предмета, то сначала необходимо выполнить проекцию ребра, а затем при помощи линий проекционной связи найти проекции точки, лежащей на ребре.

Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.

Общий метод определения точки, лежащей на поверхности геометрического тела, заключается в следующем: через точку на поверхности проводят вспомогательную прямую, проекции которой легко определяются на данной поверхности.

Построение проекции точки, лежащей на грани
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности четырехгранной пирамиды.

Проекции точек можно определить несколькими способами. Рассмотрим каждый из них.

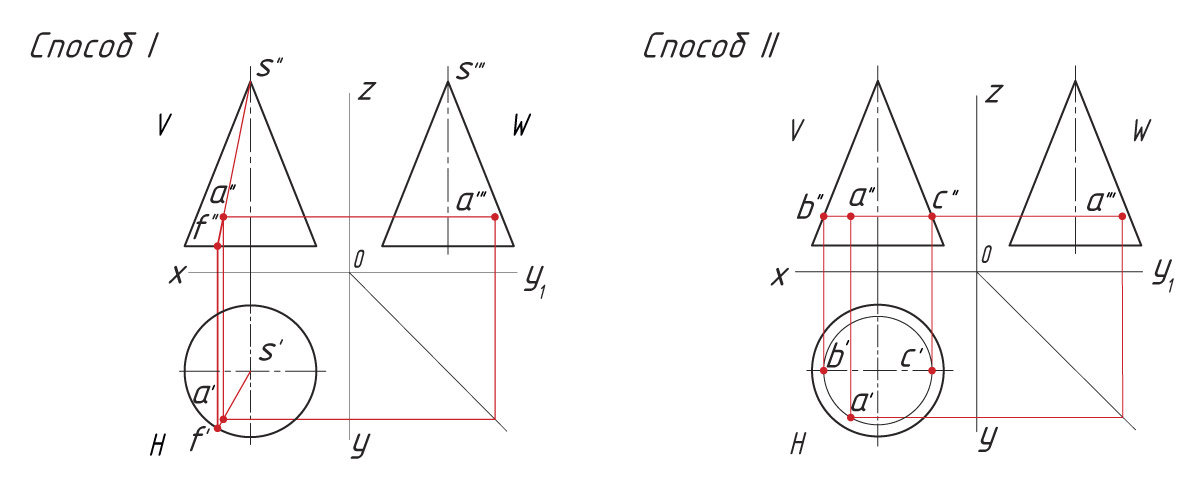
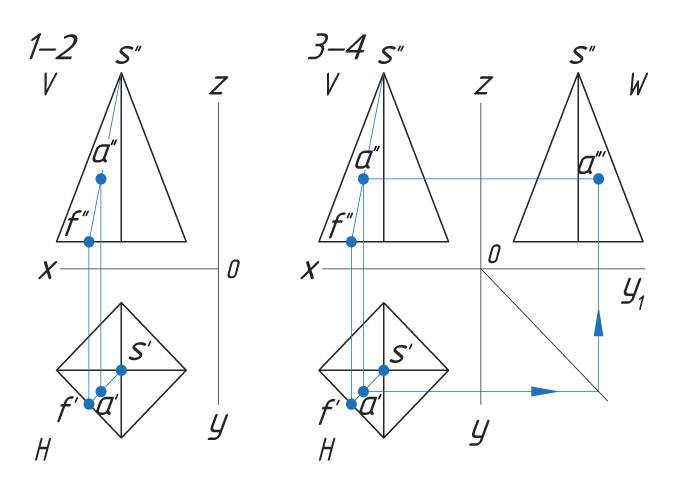
Способ I.

1. Находят горизонтальную проекцию точки а′: вспомогательной прямой соединяют заданную проекцию точки а″ с проекцией вершины пирамиды s″ и продлевают ее до пересечения с основанием в точке f″.
2. Проводят вертикальную линию связи из проекции f″ до пересечения с основанием на плоскости H в точке f′.
3. Точку f′ соединяют с вершиной пирамиды s′. На нее проводят вертикальную линию связи из проекции а″ до пересечения в точке а′.
4. Проекции точки а′″ находят на пересечении линий проекционной связи.

Способ II.

1. Через проекцию а″ точки А проводят вспомогательную прямую и получают точки пересечения с ребрами пирамиды 1″ и 2″.
2. Опустив из точки 1″ вертикальную линию связи до пересечения с соответствующим ребром на плоскости H, получают горизонтальную проекцию точки 1′.
3. Для нахождения проекции 2′ проводят из точки 1′ вспомогательную прямую, параллельную основанию до пересечения с ребром.
4. Горизонтальную проекцию а′ определяют, опустив вертикальную линию связи из точки а″ до пересечения со вспомогательной прямой 1′2′.
5. Проекцию точки а′″ находят на пересечении линий проекционной связи.

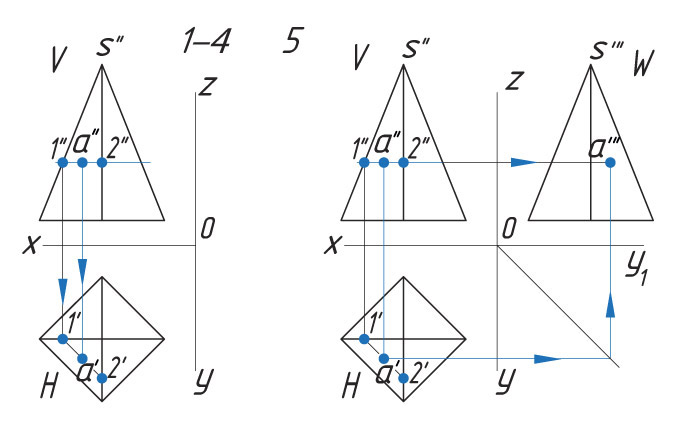На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?

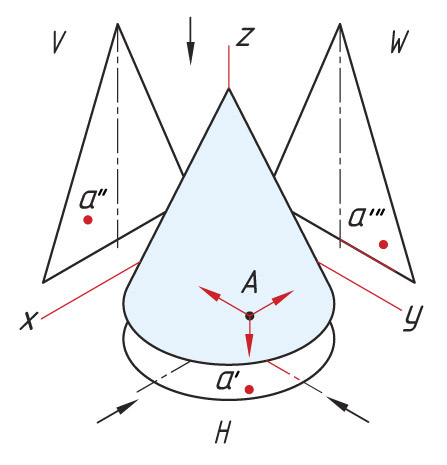
Проецирование точек на поверхности конуса. На поверхности конуса проекции точек можно также определить двумя способами.

Способ I заключается в определении проекций точки с помощью вспомогательной линии — образующей, расположенной на поверхности конуса и проведенной через точку А.
В способе II через точку А проводят вспомогательную плоскость, которая пересечет конус по окружности, расположенной в плоскости, параллельной основанию конуса.

Источник

Проецирование точки

Подробности: Категория: Основы начертательной геометрии

ПРОЕЦИРОВАНИЕ ТОЧКИ НА ДВЕ ПЛОСКОСТИ ПРОЕКЦИЙ

Образование отрезка прямой линии АА₁ можно представить как результат перемещения точки А в какой-либо плоскости Н (рис. 84, а), а образование плоскости — как перемещение отрезка прямой линии АВ (рис. 84, б).

Точка — основной геометрический элемент линии и поверхности, поэтому изучение прямоугольного проецирования предмета начинается с построения прямоугольных проекций точки.

В пространство двугранного угла, образованного двумя перпендикулярными плоскостями — фронтальной (вертикальной) плоскостью проекций V и горизонтальной плоскостью проекций Н, поместим точку А (рис. 85, а).

Линия пересечения плоскостей проекций — прямая, которая называется осью проекций и обозначается буквой х.

Плоскость V здесь изображена в виде прямоугольника, а плоскость Н — в виде параллелограмма. Наклонную сторону этого параллелограмма обычно проводят под углом 45° к его горизонтальной стороне. Длина наклонной стороны берется равной 0,5 ее действительной длины.

Из точки А опускают перпендикуляры на плоскости V и Н. Точки а’и а пересечения перпендикуляров с плоскостями проекций V и Н являются прямоугольными проекциями точки А. Фигура Ааа_ха’ в пространстве — прямоугольник. Сторона аах этого прямоугольника на наглядном изображении уменьшается в 2 раза.

Совместим плоскости Н с плоскостью V ,вращая V вокруг линии пересечения плоскостей х. В результате получается комплексный чертеж точки А (рис. 85, б)

Для упрощения комплексного чертежа границы плоскостей проекций V и Н не указывают (рис. 85, в).

Перпендикуляры, проведенные из точки А к плоскостям проекций, называются проецирующими линиями, а основания этих проецирующих линий — точки а и а’ — называются проекциями точки А: а’ — фронтальная проекция точки А, а — горизонтальная проекция точки А.

Линия а’ а называется вертикальной линией проекционной связи.

Расположение проекции точки на комплексном чертеже зависит от положения этой точки в пространстве.

Если точка А лежит на горизонтальной плоскости проекций Н (рис. 86, а), то ее горизонтальная проекция а совпадает с заданной точкой, а фронтальная проекция а’ располагается на оси При расположении точки В на фронтальной плоскости проекций V ее фронтальная проекция совпадает с этой точкой , а горизонтальная проекция лежит на оси х. Горизонтальная и фронтальная проекции заданной точки С, лежащей на оси х, совпадают с этой точкой. Комплексный чертеж точек А, В и С показан на рис. 86, б.

ПРОЕЦИРОВАНИЕ ТОЧКИ НА ТРИ ПЛОСКОСТИ ПРОЕКЦИЙ

В тех случаях, когда по двум проекциям нельзя представить себе форму предмета, его проецируют на три плоскости проекций. В этом случае вводится профильная плоскость проекций W, перпендикулярная плоскостям V и Н. Наглядное изображение системы из трех плоскостей проекций дано на рис. 87, а.

Ребра трехгранного угла (пересечение плоскостей проекций) называются осями проекций и обозначаются x, у и z. Пересечение осей проекций называется началом осей проекций и обозначается буквой О. Опустим из точки А перпендикуляр на плоскость проекций W и, отметив основание перпендикуляра буквой а», получим профильную проекцию точки А.

Для получения комплексного чертежа точки А плоскости Н и W совмещают с плоскостью V, вращая их вокруг осей Ох и Oz. Комплексный чертеж точки А показан на рис. 87, б и в.

Отрезки проецирующих линий от точки А до плоскостей проекций называются координатами точки А и обозначаются: х_А, у_А и z_A.

Например, координата z_A точки А, равная отрезку а’а_х (рис. 88, а и б), есть расстояние от точки А до горизонтальной плоскости проекций Н. Координата у точки А, равная отрезку аа_х, есть расстояние от точки А до фронтальной плоскости проекций V. Координата х_А, равная отрезку аа_у — расстояние от точки А до профильной плоскости проекций W.

Таким образом, расстояние между проекцией точки и осью проекции определяют координаты точки и являются ключом к чтению ее комплексного чертежа. По двум проекциям точки можно определить все три координаты точки.

Если заданы координаты точки А (например, х_А=20 мм, у_А=22мм и z_A= 25 мм), то можно построить три проекции этой точки.

Для этого от начала координат О по направлению оси Oz откладывают вверх координату z_A и вниз координату у_А.Из концов отложенных отрезков — точек a_z и а_у (рис. 88, а) — проводят прямые, параллельные оси Ох, и на них откладывают отрезки, равные координате х_А. Полученные точки а’ и а — фронтальная и горизонтальная проекции точки А.

По двум проекциям а’ и а точки А построить ее профильную проекцию можно тремя способами:

1) из начала координат О проводят вспомогательную дугу радиусом Оа_у, равным координате (рис. 87, б и в), из полученной точки а_у1 проводят прямую, параллельную оси Oz, и откладывают отрезок, равный z_A;

2) из точки а_у проводят вспомогательную прямую под углом 45° к оси Оу (рис. 88, а), получают точку а_у1 и т. д.;

3) из начала координат О проводят вспомогательную прямую под углом 45° к оси Оу (рис. 88, б), получают точку а_у1 и т. д.

Источник

Описание презентации по отдельным слайдам:

1 слайд

ПОСТРОЕНИЕ ПРОЕКЦИЙ ТОЧЕК НА ПОВЕРХНОСТИ ПРЕДМЕТА
2 слайд

ВЕРШИНА – это точка пересечения трех и более ребер.
РЕБРО – отрезок соединяющий соседние вершины.
ГРАНЬ – это плоскость объемной фигуры, ограниченная ребрами.
ЭЛЕМЕНТЫ ПОВЕРХНОСТИ ПРЕДМЕТА

Любая точка или отрезок на изображении предмета является проекцией того или иного элемента: вершины, ребра, грани или кривой поверхности
3 слайд

ПОСТРОЕНИЕ ПРОЕКЦИЙ ТОЧКИ НА РЕБРЕ ПИРАМИДЫ
4 слайд

Для того, чтобы правильно находить проекции отдельных точек, лежащих на гранях, нужно прежде всего найти проекции этой грани, а затем при помощи линий связи отыскать проекции точек.
ПОСТРОЕНИЕ ПРОЕКЦИЙ ТОЧЕК НА ПОВЕРХНОСТИ ПРЕДМЕТА
5 слайд

ПОСТРОЕНИЕ ПРОЕКЦИЙ ТОЧЕК НА ПОВЕРХНОСТИ ПРЕДМЕТА
6 слайд

ПОСТРОЕНИЕ ПРОЕКЦИЙ ТОЧКИ , ЛЕЖАЩЕЙ НА ПОВЕРХНОСТИ КОНУСА

Источник

Проекция – это способ изображения объемной фигуры на проекционной полости.

Виды проекций на чертеже по ГОСТу

Согласно ГОСТ 2.305-2008 и правилам аксонометрии предусматривается использование нескольких видов проекций на чертеже:

ортогональная проекция или прямоугольная проекция, предполагает перенос изображения на плоскость, перпендикулярную направлению лучей предмета или его части;
параллельная проекция получается путем проецирования предмета или его части параллельным пучком лучей на плоскость.

Как расположены проекции на чертеже

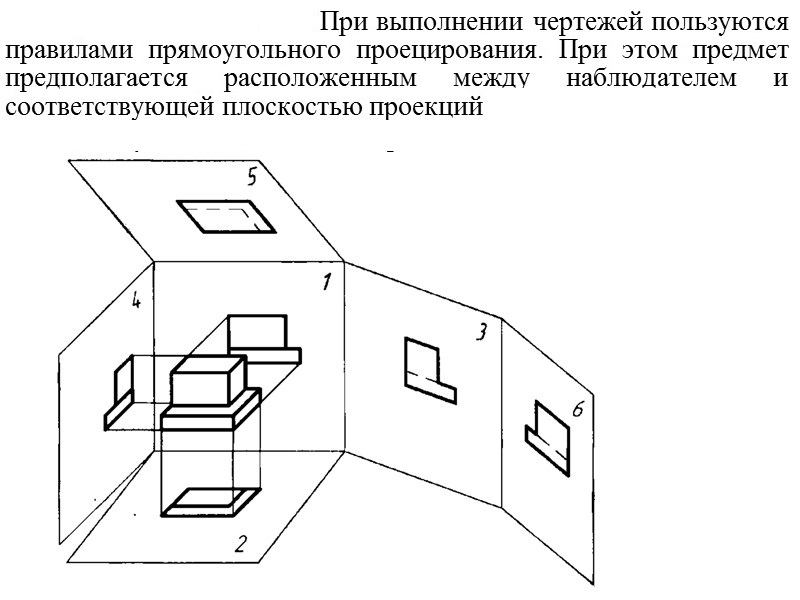
При выполнении чертежей используется метод прямоугольного проецирования и предполагается, что некий предмет, элемент или деталь располагаются между наблюдателем и плоскостью проекции. В качестве плоскостей проекции используются шесть граней куба. Фронтальная проекция считается главным видом, поэтому расположение предмета должно быть таким, чтобы на этой проекция было отражено полное представление о форме и размерах.

Рисунок 1. Шесть плоскостей проекций

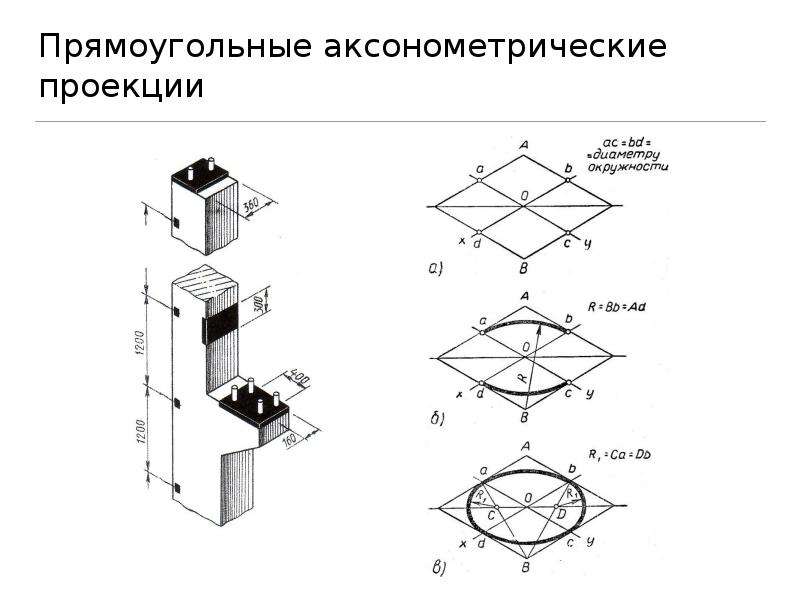
Аксонометрические проекции на чертеже

Работа по выполнению аксонометрических проекций начинается с построения осей. Оси необходимо построить в трех направлениях: горизонтальная ось Х, вертикальная ось Y и ось, идущая под углом – Z.В изометрической проекции вертикальная и горизонтальная ось располагаются под углом в тридцать градусов к горизонтальной линии.

В аксонометрической проекции масштабы по всем осям равны.

Рисунок 2. Аксонометрическая проекция

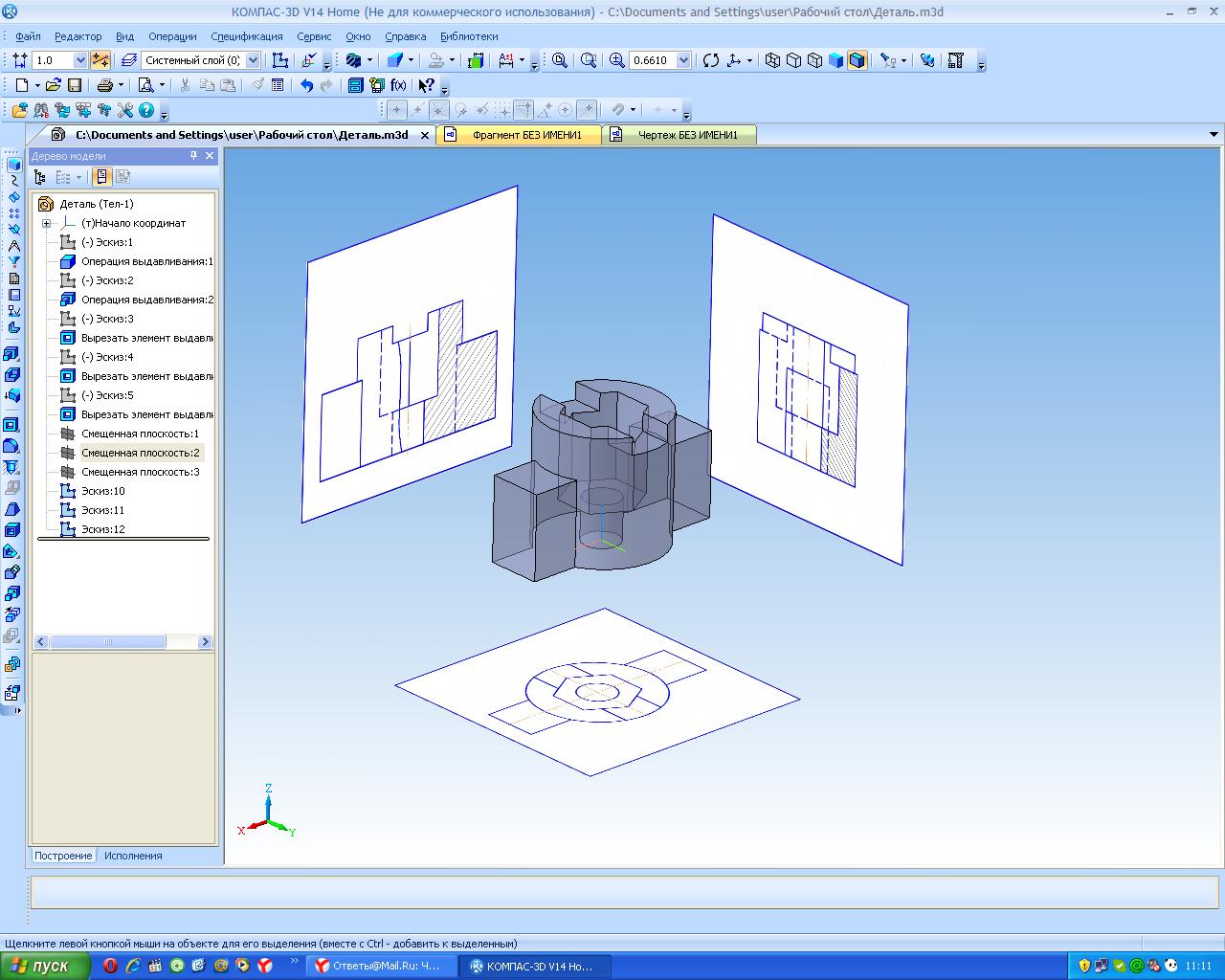
Аксонометрическая проекция по чертежу в Компас

При выполнении аксонометрической проекции в программе Компас работа сводятся к построению проекций точек и их соединению в определённой последовательности.

Рассмотрим порядок действий на примере прямоугольника. Вначале в меню «Создать» выбираем «Деталь», в «Дерево модели» раскрываем меню «Начало координат» и выбираем плоскость ХY, затем переходим в двухмерное построение, нажимаем инструмент «Прямоугольник» вводим соответствующие размеры. Закрыв двухмерный эскиз переходим, в трехмерный режим создания детали. С помощью инструмента «Выдавливание» создаем объект.

Рисунок 3. Аксонометрическая проекция в Компас

Горизонтальные проекции на чертеже

Построение горизонтальных и вертикальных проекций выполняется достаточно легко, для этого необходимо перенести изображение предмета с помощью проекционных лучей. Профильная плоскость называется так, поскольку дает полное представление о детали. Профильная плоскость располагается вертикально, справа от детали. Комплексный чертеж содержит все три проекции.

Рисунок 4. Горизонтальная, вертикальная и профильная проекции

Изометрические проекции на чертеже

Изометрическая проекция является разновидностью аксонометрической, которая позволяет отобразить трехмерный объект с одинаковым коэффициентом искажения по всем осям. Изометрическая проекция может быть прямоугольной, косоугольной фронтальной и косоугольной горизонтальной.

Дальнейший порядок построения предполагает построение передней грани детали, откладывая фактические размеры высоты вдоль оси Z, а длины вдоль горизонтальной оси X. Затем строят ребра, они идут параллельно оси Y, их длина соответствует толщине детали. В изометрическом изображении откладывается действительная длина, в диметрической проекции построены меньше в два раза. Затем полученные точки соединяют прямыми, параллельными передней фронтальной плоскости и удаляют невидимый контур.

Рисунок 5. Изометрические проекции

Проекции пересекающихся прямых на комплексном чертеже

Существует несколько способов задания плоскости, в том числе с помощью пересекающихся линий. На комплексном чертеже проекции плоскости задаются проекциями элементов. Проекции точки пересечения прямых всегда находятся на одной линии связи.

Рисунок 6. Пересекающиеся прямые на плоскости проекции

Чертеж в трех проекциях

Для выполнения чертежа используется метод ортогонального проецирования, который позволяет начертить любое техническое изделие. В ортогональном проецировании лучи параллельны друг другу и перпендикулярны плоскости, но на каждой проекции видны лишь два измерения (высота и длина). Поэтому лишь три проекции дают полное представление о трехмерном предмете. В совмещенных на одном листе чертежах можно найти точные сведения о всех геометрических характеристиках детали.

Рисунок 7. Чертеж в трех проекциях

Чертежи в системе прямоугольных проекций

Согласно названию используют ортогональное проецирование на одну, две или три плоскости. Если плоскость расположена перед наблюдающим, то она называется фронтальной, проекция на нее строится первой. Предмет располагается так, чтобы его поверхности были параллельными плоскости проекции. Выполнив построение в двух плоскостях проекции, можно получить основные данные о высоте, ширине и длине детали и мысленно представить себе ее в объеме. Но этой информации недостаточно для выявление характерных особенностей, к примеру формы выемки в детали, поэтому требуется третья проекция.

Как сделать чертеж в трех проекциях в Компас

Чтобы выполнить чертеж и совместить на одном листе три проекции, вначале нужно воспользоваться командой «Новый чертеж». Затем выберите формат листа, чтобы разместить все 3 изображения, приведенные в модели (потребуется формат А3 или А4). Затем выбираем виды и то, как они будут расположены на чертеже, через команду «Вид» основного меню.

Рисунок 8. Чертеж в трех проекциях в Компасе

Ответы на вопросы

Как обозначаются изометрические проекции?

Чтобы показать изометрическую проекцию используют обозначение осей, также показывают углы между осями.

Как найти проекцию точек по заданному положению на поверхности предмета?

Построение начинается с построения проекции поверхности, на которой расположена отдельная заданная точка, а затем проводят линию связи к проекции, где поверхность изображена линией и находят вторую проекцию точки, третья проекция будет лежат на пересечении линий связи.

Рисунок 9. Построение проекций точек, заданных на поверхности предмета

Как расположить проекции на чертеже?

Виды располагаются в проекционной связи. Главный вид располагается в левом верхнем углу, вид сверху располагается под ним, справа от главного вида расположен вид слева (сбоку).

Источник

Гипермаркет знаний>>Черчение 9 класс>>Черчение: Построение проекций точки, лежащей на поверхности предмета

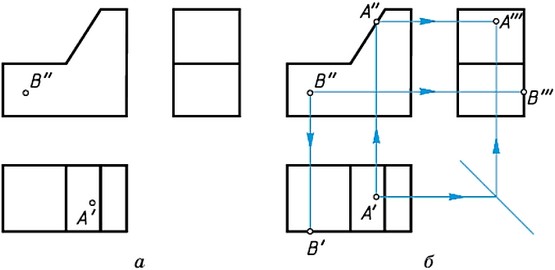
Чтобы построить проекции точки, заданной на поверхности детали, необходимо понять, на какой поверхности или на каком элементе поверхности (на ребре, вершине, образующей грани) находится эта точка, а затем уточнить ее геометрическое расположение относительно плоскостей проекций или какого-либо другого элемента формы. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки.

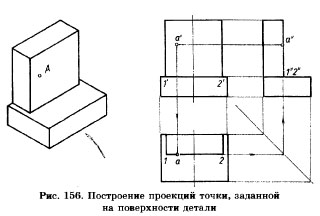
Рассмотрим пример, когда точка А задана на виде спереди фронтальной проекцией — а’. Необходимо найти остальные проекции точки А (рис. 156). По чертежу определяем, что точка находится на передней грани верхнего параллелепипеда. Чтобы найти горизонтальную проекцию точки А, надо найти на виде сверху горизонтальную проекцию грани, а затем провести линию проекционной связи от а’ до пересечения с горизонтальной проекцией грани, на которой она находится. Точка пересечения а будет являться горизонтальной проекцией точки А.

Чтобы найти профильную проекцию точки А, надо из точки а’ провести линию проекционной связи до пересечения с линией, являющейся проекцией грани, на которой находится точка. Таким образом на виде слева получим профильную проекцию а» точки А. Направление линий проекционной связи на чертеже показано стрелками.

Расположение точек на поверхности детали

Вопросы и задания
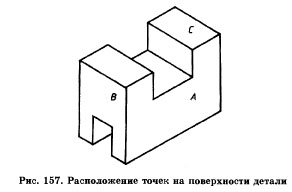
1. Рассмотрите изображение, представленное на рис. 157, и ответьте на вопросы:

Как называется изображение, выполненное на рис. 157?
Сколько плоскостей симметрии имеет деталь?
Как называется вырез на детали снизу?
Проанализируйте, из каких геометрических тел состоит форма детали?
Сколько вертикальных граней имеет деталь?
Сколько горизонтальных граней имеет деталь?
Сколько ребер, перпендикулярных горизонтальной (вертикальной) плоскости, имеет деталь?
Сколько вершин имеет деталь?

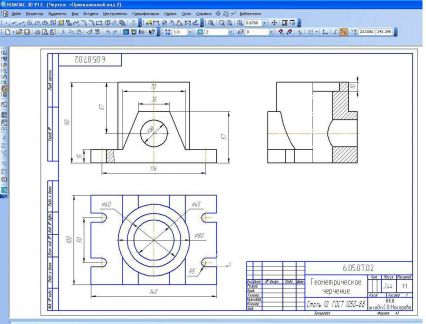
2. На рис. 158 представлен чертеж, содержащий три вида детали «Ползун». Используя кальку, переснимите на нее изображения чертежа. Найдите и обозначьте проекции точек А, В, С.
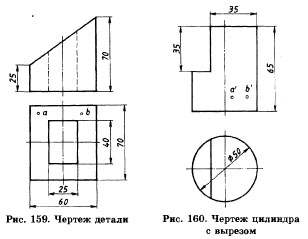
3. По чертежу детали (рис. 159) ответьте на вопросы:

Какие изображения даны на чертеже? Назовите их.
Чему равны габаритные размеры детали?
Из каких геометрических тел состоит деталь?
Сколько у детали граней?
Сколько у детали ребер и вершин?
На чертеже заданы проекции точек А и В. Какая из них расположена ближе к горизонтальной плоскости проекций?

4. Прочитайте чертежи, представленные на рис. 160, 161, и ответьте на вопросы:

Чему равны габаритные размеры деталей?
Какая из двух точек (А или В), заданных на чертежах проекциями, расположена ближе к фронтальной и профильной плоскостям проекций?

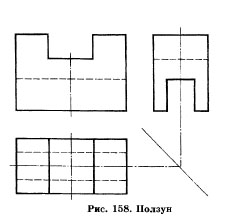
Ползун

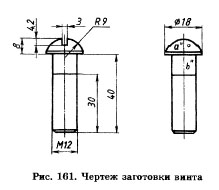
Чертеж заготовки винта

Н.А.Гордеенко, В.В.Степакова — Черчение.,9 класс
Отослано читателями из интернет-сайтов

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.

Разработка — Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email:

Источник

Проекции точек на поверхностях геометрических тел

Проецирование точки

ПРОЕЦИРОВАНИЕ ТОЧКИ НА ДВЕ ПЛОСКОСТИ ПРОЕКЦИЙ

ПРОЕЦИРОВАНИЕ ТОЧКИ НА ТРИ ПЛОСКОСТИ ПРОЕКЦИЙ

Описание презентации по отдельным слайдам:

Виды проекций на чертеже по ГОСТу

Как расположены проекции на чертеже

Аксонометрические проекции на чертеже

Аксонометрическая проекция по чертежу в Компас

Горизонтальные проекции на чертеже

Изометрические проекции на чертеже

Проекции пересекающихся прямых на комплексном чертеже

Чертеж в трех проекциях

Чертежи в системе прямоугольных проекций

Как сделать чертеж в трех проекциях в Компас

Ответы на вопросы

Как обозначаются изометрические проекции?

Как найти проекцию точек по заданному положению на поверхности предмета?

Как расположить проекции на чертеже?

Не пропустите также: