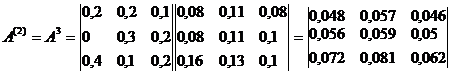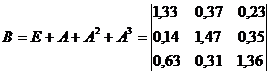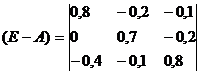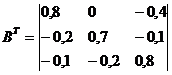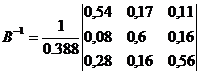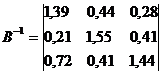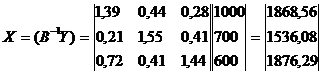Как найти продуктивность матрицы прямых затрат

Если ввести в
рассмотрение матрицу коэффициентов
прямых затрат A = (a_ij),
вектор-столбец валовой продукции X =
(X_i)
и вектор-столбец конечной продукции Y
= (Y_i),
то математическая
модель межотраслевого баланса
примет вид:

X = AX +Y

Идея
сбалансированности лежит в основе
всякого рационального функционирования
хозяйства. Суть ее в том, что все затраты
должны компенсироваться доходами
хозяйства. В основе создания балансовых
моделей лежит балансовый метод –
взаимное сопоставление имеющихся
ресурсов и потребностей в них.

Межотраслевой
баланс отражает
производство и распределение валового
национального продукта в отраслевом
разрезе, межотраслевые производственные
связи, использование материальных и
трудовых ресурсов, создание и распределение
национального дохода.

Пусть экономика
страны имеет n
отраслей материального производства.
Каждая отрасль выпускает некоторый
продукт, часть которого потребляется
другими отраслями (промежуточный
продукт), а другая часть – идет на
конечное потребление и накопление
(конечный продукт).

Обозначим через
X_i
(i=1..n) валовый продукт i-й
отрасли; x_ij
– стоимость продукта, произведенного
в i-й
отрасли и потребленного в j-й
отрасли для изготовления продукции
стоимостью X_j;
Y_i
– конечный продукт i-й
отрасли.

Критерии
продуктивности матрицы А

Существует несколько критериев
продуктивности матрицы А.

1. Матрица
А продуктивна, если максимум сумм
элементов ее столбцов не превосходит
единицы, причем хотя бы для одного из
столбцов сумма элементов строго меньше
единицы.

2. Для того чтобы обеспечить
положительный конечный выпуск по всем
отраслям необходимо и достаточно, чтобы
выполнялось одно из перечисленных ниже
условий:

3. Определитель матрицы (E —
A) не равен нулю, т.е. матрица (E- A) имеет
обратную матрицу (E — A)^-1.

4. Наибольшее по модулю собственное
значение матрицы А, т.е. решение уравнения
|λE — A| = 0 строго меньше единицы.

5. Все
главные миноры матрицы (E — A) порядка от
1 до n, положительны.

Рассмотрим
три отрасли промышленности: I, II, III,
каждая из которых производит свой
однородный продукт и для обеспечения
производства нуждается в продукции
других отраслей. Процесс производства
рассматривается за определенный период
времени. Взаимодействие отраслей
определяется матрицей А прямых затрат.
Задан вектор y объемом продуктов конечного
потребления.

а) определить, является
ли матрица продуктивной;

б) составить
уравнение межотраслевого баланса;

в)
найти объем валовой продукции каждой
отрасли;

г) составить матрицу потоков
средств производства;

Определить,
будут ли следующие матрицы продуктивны.

Матрица A имеет неотрицательные
элементы и удовлетворяет критерию
продуктивности
(при любом j
сумма элементов столбца ∑a_ij
≤ 1.

Пример1.
Определим матрицу коэффициентов полных
материальных затрат приближенно,
учитывая косвенные затраты до 2-го
порядка включительно.

а) Матрица
коэффициентов косвенных затрат 1-го
порядка равна:

б)
Матрица коэффициентов косвенных затрат
2-го порядка равна:

Матрица
коэффициентов полных затрат приближенно
равна:

пример2
Определим матрицу коэффициентов полных
затрат точно
с помощью формул обращения невырожденных
матриц.

Коэффициент полных затрат
(b_ij)
показывает, какое количество продукции
i-й
отрасли нужно произвести, чтобы с учетом
прямых и косвенных затрат этой продукции
получить единицу конечной продукции
j-й
отрасли.

Полные затраты отражают
использование ресурса на всех этапах
изготовления и равны сумме прямых и
косвенных затрат на всех предыдущих
стадиях производства продукции.

а)
Находим матрицу (E-A):

б)
Вычисляем обратную матрицу (E-A)^-1:

Запишем матрицу в виде:

Главный
определить

∆ = 0.8 • (0.7 • 0.8-(-0.1 •
(-0.2)))-0 • (-0.2 • 0.8-(-0.1 • (-0.1)))+(-0.4 • (-0.2 •
(-0.2)-0.7 • (-0.1))) = 0.388

Транспонированная
матрица

Алгебраические
дополнения

∆_1,1
= (0.7 • 0.8-(-0.2 • (-0.1))) = 0.54

∆_1,2
= -(-0.2 • 0.8-(-0.1 • (-0.1))) = 0.17

∆_1,3
= (-0.2 • (-0.2)-(-0.1 • 0.7)) = 0.11

∆_2,1
= -(0 • 0.8-(-0.2 • (-0.4))) = 0.08

∆_2,2
= (0.8 • 0.8-(-0.1 • (-0.4))) = 0.6

∆_2,3
= -(0.8 • (-0.2)-(-0.1 • 0)) = 0.16

∆_3,1
= (0 • (-0.1)-0.7 • (-0.4)) = 0.28

∆_3,2
= -(0.8 • (-0.1)-(-0.2 • (-0.4))) = 0.16

∆_3,3
= (0.8 • 0.7-(-0.2 • 0)) = 0.56

Обратная
матрица

Найдем
величины валовой продукции трех отраслей

Для
определения элементов первого квадранта
материального межотраслевого баланса
воспользуемся формулой x_ij
= a_ij
• X_j.

Составляющие третьего квадранта
(условно-чистая продукция) находятся
как разность между объемами валовой
продукции и суммами элементов
соответствующих столбцов найденного
первого квадранта.

Межотраслевой
баланс состоит из четырех квадрантов
(табл.). Первый квадрант отражает
межотраслевые потоки продукции. Второй
характеризует отраслевую материальную
структуру национального дохода.

Третий
представляет национальный доход как
стоимость условно-чистой продукции
(Z_j),
равной сумме амортизации (c_j),
оплаты труда (v_j)
и чистого дохода j-й
отрасли (m_j).
Четвертый квадрант показывает конечное
распределение и использование
национального дохода.

Применение
межотраслевого баланса для анализа
экономического показателя труда.

Различные модификации рассмотренной
выше модели межотраслевого баланса
производства и распределения продукции
в народном хозяйстве позволяют расширить
круг показателей, охватываемых моделью.

40. модель Леонтьева
в натуральной и стоимостной форме.

17

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Задача

Экономика
представлена двумя отраслями производства: промышленностью и сельским
хозяйством. За отчетный период получены следующие данные о межотраслевых
поставках

 и векторе объемов конечного использования

.

Требуется:

Указание:
При вычислениях производить округление с точностью до тысячных.

Решение

Матрица прямых затрат

Найдем
валовые выпуски отраслей, просуммировав в каждой строке межотраслевые поставки
и координату вектора

:

Найдем
матрицу прямых затрат. Ее элементы можно найти по формуле:

Подставляя
числовые значения, получаем:

Матрица «Затраты — выпуск»

Найдем матрицу
«Затраты — выпуск»

Вектор конечного использования Y для валового объема выпуска X

Вектор
конечного использования Y для валового объема выпуска X определим на основе
балансового соотношения: 

Для этого выполним умножение двух матриц

Матрица полных затрат

Найдем
матрицу коэффициентов полных материальных затрат

 -она будет равна обратной матрице

:

Определитель матрицы

:

Алгебраические
дополнения:

Обратная матрица:

Вектор валового объема выпуска X для конечного использования Y

Вектор валового объема выпуска

 для конечного продукта

 определим формуле:

Приросты валовых объемов выпуска

Найдем
приросты валовых объемов выпуска, если конечное потребление должно изменяться
на

 по сравнению с

:

Матрица полных затрат ресурсов S

Найдем
матрицу полных затрат ресурсов S для заданной матрицы ее прямых затрат M:

Суммарная потребность в ресурсах

Суммарная  потребность в ресурсах для вектора Y₀:

Суммарная  потребность в ресурсах для вектора Y_n:

Матрицы косвенных затрат и сумма затрат

Найдем
матрицы косвенных затрат первого, второго и третьего порядка

Сумма затрат:

Разность
матриц:

Вектор потребности в продукции

Найдем
вектор потребности в продукции всех отраслей материального производства b_ij
для получения единицы конечного продукта b_j вида. Для этого
просуммируем столбцы матрицы полных затрат:

Это значит, что для производства
единицы конечного продукта в первой отрасли во всех отраслях надо расходовать
продукции на сумму 1,913 ден.ед., для производства единицы конечного продукта
во второй отрасли -на 2,021 ден.ед.

Матрица А, все элементы которой неотрицательны, на­зывается продуктивной, если для любого вектора с неот­рицательными компонентами существует решение уравнения (16.6) — вектор , все элементы которого неотрицательны. В таком случае и модель Леонтьева называется продуктивной.

Для уравнения типа (16.6) разработана соответствующая математическая теория исследования решения и его особеннос­тей. Укажем некоторые ее основные моменты. Приведем без доказательства важную теорему, позволяющую устанавливать продуктивность матрицы.

ТЕОРЕМА 16.1. Если для матрицы А с неотрицательными элементами и некоторого вектора с неотрицательными компонентами уравнение (16.6) имеет решение с неотри­цательными компонентами, то матрица А продуктивна.

Иными словами, достаточно установить наличие положи­тельного решения системы (16.6) хотя бы для одного положи­тельного вектора , чтобы матрица А была продуктивной. Пе­репишем систему (16.6) с использованием единичной матрицы Е в виде

Если существует обратная матрица (E — А)-1 , то существует и единственное решение уравнения (16.7):

Матрица (Е — А)-1 называется Матрицей полных затрат.

Существует несколько критериев продуктивности матри­цы А. Приведем два из них.

Первый критерий продуктивности. Матрица А продукти­вна тогда и только тогда, когда матрица (Е — А)-1 сущест­вует и ее элементы неотрицательны.

Второй критерий продуктивности. Матрица А с неотри­цательными элементами продуктивна, если сумма элемен­тов по любому ее столбцу (строке) не превосходит единицы:

Причем хотя бы для одного столбца (строки) эта сумма строго меньше единицы.

Рассмотрим применение модели Леонтьева на несложных примерах.

Пример 1. В табл. 16.4 приведены данные по балансу за не­который период времени между пятью отраслями промышлен­ности. Найти векторы конечного потребления и валового вы­пуска, а также матрицу коэффициентов прямых затрат и опре­делить, является ли она продуктивной в соответствии с при­веденными выше критериями.

Решение. В данной таблице приведены составляющие ба­ланса в соответствии с соотношениями (16.2): Xij — первые пять столбцов, Уi — шестой столбец, Xi — последний столбец (I,J = 1, 2, 3, 4, 5). Согласно формулам (16.3) и (16.4), имеем

Все элементы матрицы А положительны, однако нетрудно видеть, что их сумма в третьем и четвертом столбцах боль­ше единицы. Следовательно, условия второго критерия продук­тивности не соблюдены и матрица А не является продуктив­ной. Экономическая причина этой непродуктивности заключа­ется в том, что внутреннее потребление отраслей 3 и 4 слиш­ком велико в соотношении с их валовыми выпусками.

Пример 2. Табл. 16.5 содержит данные баланса трех отрас­лей промышленности за некоторый период времени. Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление по отраслям увеличить соответственно до 60, 70 и 30 условных денежных единиц.

Решение. Выпишем векторы валового выпуска и конеч­ного потребления и матрицу коэффициентов прямых затрат. Согласно формулам (16.3) и (16.4), имеем

Матрица А удовлетворяет обоим критериям продуктивности. В случае заданного увеличения конечного потребления новый вектор конечного продукта будет иметь вид

Требуется найти новый вектор валового выпуска *, удов­летворяющий соотношениям баланса в предположении, что матрица А не изменяется. В таком случае компоненты X1, X2, х3 неизвестного вектора * находятся из системы уравнений, которая согласно (16.4) имеет в данном случае вид

В матричной форме эта система выглядит следующим об­разом:

Или

Где матрица (Е — А) имеет вид

Решение системы линейных уравнений (16.11) при заданном векторе правой части (16.9) (например, методом Гаусса) да­ет новый вектор * как решение системы уравнений баланса (16.10):

Таким образом, для того чтобы обеспечить заданное уве­личение компонент вектора конечного продукта, необходимо увеличить соответствующие валовые выпуски: добычу и пе­реработку углеводородов на 52,2%, уровень энергетики — на 35,8% и выпуск продукции машиностроения — на 85% по срав­нению с исходными величинами, указанными в табл. 16.5.