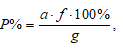Формулы для расчета процентного содержания металлов в сплаве приведены под калькулятором.
Процентное содержание металлов в сплаве
Плотность первого металла
Плотность второго металла
Точность вычисления
Знаков после запятой: 2
Процентное содержание первого металла
Процентное содержание второго металла
Расчет процентного содержания металлов в сплаве двух металлов
Пусть нам известны физические характеристики сплава, масса и плотность, их можно просто померять, и плотности металлов, составляющих сплав (например, их можно узнать из справочника).
Имеем следующие очевидные соотношения:
,
где
m — масса сплава,
V — объем сплава,
m₁ — масса первого металла,
V₁ — объем первого металла,
ρ₁ — плотность первого металла,
m₂ — масса второго металла,
V₂ — объем второго металла,
ρ₂ — плотность второго металла.
m₁, V₁, m₂, V₂ — четыре неизвестных на четыре уравнения — существует единственное решение.
Выполнив подстановки, можно получить довольно громоздкие формулы для m₁ и m₂
Процентные соотношения получим, поделив массы металлов на массу сплава.
Вычисление процентного содержания кадмия, свинца и хлорида калия в аналитическом образце сплава или соли
Вычисление процентного содержания кадмия в образце сплава
Задача 180.
Вычислите процентное содержание определяемого вещества в аналитическом образце по следующим данным: исследуемый образец сплав, навеска массой 1,2018г; определяемое вещество Cd; весовая форма Cd2P2O7, массой равной 0,4273г.
Решение:
Расчёт процентного содержания определяемого вещества в пробе проводим по формуле:
где
а — масса весовой формы определяемого вещества, г;
f- аналитический множитель (фактор пересчета);
g — масса навески, г;
Р — приблизительное процентное содержание вещества в образце.
Ar(Cd) = 112,411;
Mr(Cd2P2O7) = 398,77;
f = 2Ar(Cd)/Mr(Cd2P2O7) = (2 . 112,411)/398,77 = 0,5634.
Подставив все числовые значения в расчётную формулу, получим:
Р% = (0,4273 . 0,5634 . 100%)/1,2018 = 20,05%.
Ответ: Р% = 20,05%.
Вычисление процентного содержания хлорида калия в образце соли хлорида калия
Задача 181.
Вычислите процентное содержание определяемого вещества в аналитическом образце по следующим данным: исследуемый образец калия хлорид, навеска массой 0,9617г; определяемое вещество KCl; весовая форма K2PtCl6, массой равной 0,4716г.
Решение:
Расчёт процентного содержания определяемого вещества в пробе проводим по формуле:
где
а — масса весовой формы определяемого вещества, г;
f- аналитический множитель (фактор пересчета);
g- масса навески, г;
Р — приблизительное процентное содержание вещества в образце.
Ar(KCl) = 74,55;
Mr(K2PtCl6) = 485,994;
f = 2Ar(KCl)(K2PtCl6) = (2 . 74,55)/485,994 = 0,3068.
Подставив все числовые значения в расчётную формулу, получим:
Р% = (0,4716 . 0,3068 . 100%)/0,9617 = 15,045%.
Ответ: Р% = 15,045%.
Вычисление процентного содержания свинца в образце нитрата свинца
Задача 182.
Вычислите процентное содержание определяемого вещества в аналитическом образце по следующим данным: исследуемый образец нитрат свинца, навеска массой 0,7514г; определяемое вещество Pb; весовая форма PbCrO4, массой равной 0,3518г.
Решение:
Расчёт процентного содержания определяемого вещества в пробе проводим по формуле:
где
а — масса весовой формы определяемого вещества, г;
f- аналитический множитель (фактор пересчета);
g — масса навески, г;
Р — приблизительное процентное содержание вещества в образце.
Ar(Pb) = 207,2;
Mr(PbCrO4) = 323,196;
f = Ar(Pb)/Mr(PbCrO4) = 207,2/323,196 = 0,6411.
Подставив все числовые значения в расчётную формулу, получим:
Р% = (0,3518 . 0,6411 . 100%)/0,7514 = 30,02%.
Ответ: Р% = 30,02%.
Задачи на смеси и сплавы — подробнее
Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора.
То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.
Обычно концентрация измеряется в процентах.
Что такое процент?
Напомню, что это сотая доля числа. То есть, если массу или объем разделить на ( displaystyle 100), получим ( displaystyle 1%) этой массы или объема.
Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на ( displaystyle 100%).
Почему?
Сейчас покажу: пусть масса всего раствора равна ( displaystyle M), а масса растворенного вещества (например, соли или кислоты) – ( displaystyle m). Тогда один процент от массы раствора равен ( displaystyle frac{M}{100}).
Как узнать, сколько таких процентов содержится в числе ( displaystyle m)?
Просто: поделить число ( displaystyle m) на этот один процент: ( displaystyle frac{m}{frac{M}{100}}=frac{m}{M}cdot 100), но ведь ( displaystyle frac{m}{M}) – это концентрация.
Вот и получается, что ее надо умножить на ( displaystyle 100), чтобы узнать, сколько процентов вещества содержится в растворе.
Более подробно о процентах – в темах «Дроби, и действия с дробями»и «Проценты».
Поехали дальше.
Масса раствора, смеси или сплава равна сумма масс всех составляющих.
Логично, правда?
Например, если в растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг соли, то сколько в нем воды? Правильно, ( displaystyle 7)кг.
И еще одна очевидность:
При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.
А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.
Например: в первом растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг кислоты, а во втором растворе массой ( displaystyle 14) кг – ( displaystyle 5) кг кислоты.
Когда мы их смешаем, чему будет равна масса нового раствора?
( displaystyle 10+14=24) кг.
А сколько в новом растворе будет кислоты? ( displaystyle 3+5=8) кг.
Перейдем к задачам.
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)
В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы — на все, что содержит разные вещества в каком-то соотношении.
Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).
Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.
Также мы научимся решать сложные задачи на проценты — в основном они на банковские вклады и кредиты и прочие финансовые штуки.
Это, в том числе, даст нам очень большой задел для “ экономической» задачи №17 (которая стоит аж 3 первичных балла).
ЕГЭ №17 Экономическая задача. Вклады
Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!
Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.
По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.
Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!
На этом уроке мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.
Задачи на растворы, смеси и сплавы относятся к традиционным арифметическим и алгебраическим задачам, решение которых нередко вызывает трудности. Для решения таких задач нужно уметь рассуждать и уметь решать задачи на проценты и дроби, на составление уравнений и систем уравнений.
Давайте, сначала, определим, что это за задачи на смеси и сплавы. Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты, а для этого надо четко понимать, что:
— масса раствора = масса воды + масса соли;
— масса сплава равна сумме масс металлов, входящих в этот сплав;
— масса смеси равна сумме масс компонентов этой смеси.
При решении задач на смеси, растворы и сплавы, мы используем их общее свойство, которое заключается в том, что масса смеси, раствора или сплава равна сумме масс их компонентов.
Введем понятие концентрации или процентного содержания вещества в растворе (смеси, сплаве).
Концентрация соли или процентное содержание соли в растворе — это отношение массы соли к массе раствора, записанное в виде процентов:
K=(mc/M)*100%,
где mс — масса соли, M – масса всего раствора, К – концентрация (процентное содержание) соли.
Концентрация вещества или процентное содержание вещества в смеси — это отношение массы вещества к массе смеси, записанное в виде процентов: K=(mв/M)*100%, где mв — масса вещества, M – масса всей смеси, К – концентрация (процентное содержание) вещества
Концентрация вещества или процентное содержание вещества в сплаве — это отношение массы вещества к массе сплава, записанное в виде процентов : K=(mв/M)*100%, где mв — масса вещества, M – масса всего сплава, К – концентрация (процентное содержание) вещества.
Пример раствора. Возьмем 180 грамм воды и добавим в воду 20 грамм соли. Получим раствор, его масса равна 180 + 20 = 200 грамм. Определим концентрацию соли (процентное содержание соли) в растворе: К= (20/(180+20))*100%=10% . Тогда процентное содержание воды 90%. (100%-10%=90%). Процентное содержание воды можно определить и так: Кв=(180/(180+20))*100%=90%. Результаты запишем в виде таблицы.
| соль | 20гр | 10% |
| вода | 180гр | 90% |
| раствор | 200гр | 100% |
Пример смеси. Возьмем и перемешаем одно ведро цемента с тремя ведрами песка. Получим смесь цемента с песком, её масса равна 1 + 3 = 4 (единиц массы). Определим концентрацию (процентное содержание) цемента в смеси : К=(1/(1+3))*100%=25%.. Концентрация (процентное содержание) песка в смеси 100%-25%=75%.
Результаты запишем в виде таблицы.
| цемент | 1 ведро | 25% |
| песок | 3ведра | 75% |
| смесь | 4 ведра | 100% |
Пример сплава. Сплав цинка и меди массой 600 гр. содержит 270 гр.меди. Определим концентрацию (процентное содержание) меди в сплаве:
Км= (270/600)*100%= 45%.
Концентрация (процентное содержание) цинка в смеси:
100%-45%=55%. Или Кц=((600-270)/600))*100%= 55%.
Результаты запишем в виде таблицы.
| цинк | 330 | 55% |
| медь | 270 | 45% |
| сплав | 600гр | 100% |
Масса вещества в растворе, смеси, сплаве.
Из формулы K=(m/M)*100%, где m масса вещества, М — масса всего раствора ( смеси, сплава), получим, что масса вещества в растворе находится по формуле: m=(M*K)/100%.
Например: а) Имеется 200 гр 40% раствора соли. Определите массу соли.
Решение : mc = (200*40%)/100 = 80г. Ответ: 80 г
б) Сплав меди и цинка массой 900г содержит 64% меди. Определите массу цинка в сплаве.
Решение: 1 способ. 100% — 64% = 36% цинка в смеси,
mц=(900*36%)/100%=324г.
2 способ. mм= (900*64%)/100%=576г, 900 – 576 = 324 г.
Ответ: 324г.
.
Последнее изменение: Четверг, 24 июля 2014, 21:53
Содержание
- Вычисление процентного содержания свинца, марганца и калия в аналитическом образце вещества
- Расчет процентного содержания свинца в образце сплава
- Вычисление процентного содержания марганца в образце сульфата марганца
- Вычисление процентного содержания калия в образце хлорида калия
Вычисление процентного содержания свинца, марганца и калия в аналитическом образце вещества
Расчет процентного содержания свинца в образце сплава
Задача 171.
Вычислите процентное содержание определяемого вещества в аналитическом образце по следующим данным: исследуемый образец сплав, навеска массой 2,1200г; определяемое вещество Pb; весовая форма PbCrO4, массой равной 0,6472г.
Решение:
Расчёт процентного содержания определяемого вещества в пробе проводим по формуле:
где
а — масса весовой формы определяемого вещества, г;
f- аналитический множитель (фактор пересчета);
g — масса навески, г;
Р — приблизительное процентное содержание вещества в образце.
Ar(Pb) = 207,2;
Mr(PbCrO4) = 323,196;
f = Ar(Pb)/Mr(PbCrO4) = 207,2/323,196 = 0,6411.
Подставив все числовые значения в расчётную формулу, получим:
Р% = (0,6472 . 0,6411 . 100%)/1,1200 = 19,57%.
Ответ: Р% = 19,57%.
Вычисление процентного содержания марганца в образце сульфата марганца
Задача 172.
Вычислите процентное содержание определяемого вещества в аналитическом образце по следующим данным: исследуемое вещество марганца сульфат, навеска массой 0,4318г; определяемое вещество Mn ; весовая форма Mn2P2O7, массой равной 0,1817г.
Решение:
Расчёт процентного содержания определяемого вещества в пробе проводим по формуле:
где
а — масса весовой формы определяемого вещества, г;
f- аналитический множитель (фактор пересчета);
g — масса навески, г;
Р — приблизительное процентное содержание вещества в образце.
Ar(Mn) = 54,938;
Mr(Mn2P2O7) = 228,886;
f = 2Ar(Mn)/Mr(Mn2P2O7) = (2 . 54,938)/228,886 = 0,4800.
Подставив все числовые значения в расчётную формулу, получим:
Р% = (0,1817 . 0,4800 . 100%)/0,4218 = 21,28%.
Ответ: Р% = 21,28%.
Вычисление процентного содержания калия в образце хлорида калия
Задача 173.
Вычислите процентное содержание определяемого вещества в аналитическом образце по следующим данным: исследуемое вещество калия хлорид, навеска массой 0,8717г; определяемое вещество К ; весовая форма K2PtCl6, массой равной 0,5117г.
Решение:
Расчёт процентного содержания определяемого вещества в пробе проводим по формуле:
где
а — масса весовой формы определяемого вещества, г;
f- аналитический множитель (фактор пересчета);
g — масса навески, г;
Р — приблизительное процентное содержание вещества в образце.
Ar(K) = 39,098;
Mr(K2PtCl6) = 485,994;
f = 2Ar(K)/Mr(K2PtCl6) = (2 . 39,098)/485,994 = 0,1609.
Подставив все числовые значения в расчётную формулу, получим:
Р% = (0,5117 . 0,1609 . 100%)/0,8717 = 9,45%.
Ответ: Р% = 9,45%