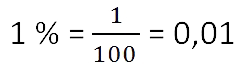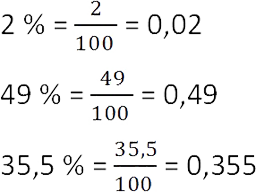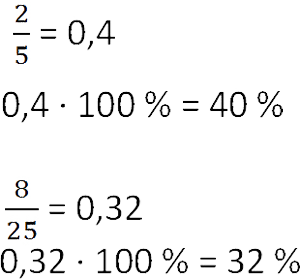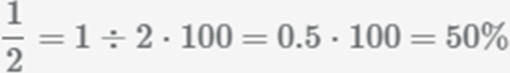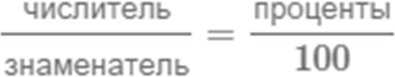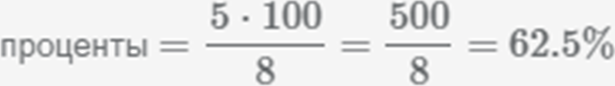Fractions are comprised of a numerator and a denominator. The denominator represents the number of parts that make up one whole, and the numerator represents the number of those parts in the fraction. For example, 3/5 would mean that five parts equals one whole, and this fraction has three parts. If you wanted to find a percentage of a fraction, you need to know how to convert a percentage to a decimal and how to multiply that decimal by the fraction.
Divide the percent by 100 to convert it to a decimal. For example, if you want to find 20 percent of 5/7, first divide 20 by 100 to get 0.2.
Multiply the decimal by the numerator of the fraction. In this example, multiply 0.2 by 5 to get 1.
Place the result from the previous step over the original denominator. In this example, you would place 1 over 7 to find that 1/7 equals 20 percent of 5/7. If you want to convert to a decimal, simply divide the numerator by the denominator. In this example, 5/7 equals 0.7143.
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Проценты в математике
Поддержать сайт
Запомните!
Процент — это одна сотая часть от числа.
Процент записывается с помощью знака «%».
-
Чтобы перевести проценты в дробь, нужно убрать знак «%» и разделить число на
100. -
Чтобы перевести десятичную дробь в проценты, нужно дробь умножить на 100 и добавить знак «%».
- 0,14 = 0,14 · 100% = 14%
- 0,07 = 0,07 · 100% = 7%
- 0,565 = 0,565 · 100% = 56,5%
-
Чтобы перевести обыкновенную дробь в проценты,
нужно сначала превратить её в десятичную дробь.
Перевод дробей в проценты
Как вы поняли, проценты тесно связаны с обыкновенными и десятичными
дробями. Поэтому стоит запомнить несколько простых равенств.
В повседневной жизни нужно
знать о числовой связи дробей и процентов. Так, половина — 50%, четверть — 25%,
три четверти — 75%, одна пятая — 20%, а три пятых — 60%.
Знание наизусть соотношений из таблицы внизу облегчит вам решение
многих задач.
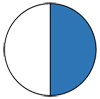
1 = 100%
| Картинка | Дробь | Десятичная дробь | Процент | ||
|---|---|---|---|---|---|
|
|
0,5 | 50% | ||

|
|
0,25 | 25% | ||

|
|
0,75 | 75% | ||

|
|
0,2 | 20% | ||

|
|
0,4 | 40% | ||

|
|
0,6 | 60% | ||

|
|
0,1 | 10% | ||

|
|
0,05 | 5% |
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
23 апреля 2023 в 22:16
Давид Суварян
Профиль
Благодарили: 0
Сообщений: 1
Давид Суварян
Профиль
Благодарили: 0
Сообщений: 1
•••—•••
0
Спасибо
Ответить
14 марта 2019 в 8:52
RED Rage-Eagerness-Demon
Профиль
Благодарили: 0
Сообщений: 1
RED Rage-Eagerness-Demon
Профиль
Благодарили: 0
Сообщений: 1
Спор с учителем, снизили оценку за то что после вычисления числа я сразу перевел в проценты
….=0.17*100%=17%
учитель учтел это за ошибку т.к нельзя так было записать надо было перенесли на новую строчку и занового переписать ответ и ег умножить на 100%
Я считаю что я прав
помогите решить спор
0
Спасибо
Ответить
18 марта 2019 в 16:31
Ответ для RED Rage-Eagerness-Demon
Micky Stepheinson
Профиль
Благодарили: 0
Сообщений: 2
Micky Stepheinson
Профиль
Благодарили: 0
Сообщений: 2
Я считаю что она сделала это правильно. Так как если задание нужно записывать по порядку, значит так надо делать. Это Для лучшего запоминания или быстрого усвоения материала 
0
Спасибо
Ответить
16 мая 2017 в 18:33
Саня Зеленский
Профиль
Благодарили: 0
Сообщений: 1
Саня Зеленский
Профиль
Благодарили: 0
Сообщений: 1
Цена кресла состовляет 45% цены дивана.Сколько рублей нужно заплатить за диван и кресло, если диван стоит 20000 рублей.
0
Спасибо
Ответить
17 мая 2017 в 9:43
Ответ для Саня Зеленский
Asel Ashirova
Профиль
Благодарили: 0
Сообщений: 1
Asel Ashirova
Профиль
Благодарили: 0
Сообщений: 1
29000p
20000 =100%
20000: 100% = 200 =1%
200 · 45%= 9000р
20000 + 9000 = 29000
0
Спасибо
Ответить
6 июля 2016 в 18:42
Ирина Поджарова
Профиль
Благодарили: 0
Сообщений: 2
Ирина Поджарова
Профиль
Благодарили: 0
Сообщений: 2
Имеется два слитка сплавов меди и олова. Первый весит 3 кг и содержит 40 % меди, второй весит 7 кг и содержит 30 % меди. Какого веса нужно взять куски этих слитков, чтобы после их совместной переплавки получить 8 кг сплава, содержащего m % меди?
0
Спасибо
Ответить
9 июля 2016 в 7:36
Ответ для Ирина Поджарова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
30% · x + 40% · (8 ? x) = m% · 8
x = 32 ? .
1 ? x ? 3.
0
Спасибо
Ответить
9 декабря 2015 в 13:44
Юрсланбек Худайбердиев
Профиль
Благодарили: 0
Сообщений: 1
Юрсланбек Худайбердиев
Профиль
Благодарили: 0
Сообщений: 1
руда содержит 70%·сколько нужно взять руды чтобы получить 42 т железа
0
Спасибо
Ответить
9 декабря 2015 в 21:45
Ответ для Юрсланбек Худайбердиев
Арутюн Гёзалян
Профиль
Благодарили: 0
Сообщений: 2
Арутюн Гёзалян
Профиль
Благодарили: 0
Сообщений: 2
1т=1000 кг соответственно 42 т=42000 кг1 т руды содержит 70% железа,70% из 1 тонны=700 кг70=700
Для того чтобы узнать сколько потребуется руды нужно 42 тонны разделить на 700 кг,700 кг-это 70% от одной тонны руды.Таким образом получаем 60 тонн.
=60
Для проверки верности решения, выполним обратное действие 700 умножим на 60, получим 42000 кг= 42т.ответ: 60 т.
0
Спасибо
Ответить
4 ноября 2015 в 16:50
Сергей Полднев
Профиль
Благодарили: 0
Сообщений: 1
Сергей Полднев
Профиль
Благодарили: 0
Сообщений: 1
федоров, иванов и петров выиграли вместе в лотерею 1800р. выигрыш иванова составляет 64% выигрыша федорова, а выигрыш петрова 76% выигрыша федорова. сколько рублей составлялвыигрыш каждого из вних?
0
Спасибо
Ответить
23 ноября 2015 в 0:59
Ответ для Сергей Полднев
?ригорий ?акаров
Профиль
Благодарили: 0
Сообщений: 1
?ригорий ?акаров
Профиль
Благодарили: 0
Сообщений: 1
Мой тут ответ: < фв 750″ a ив. 480 и,570. > чао.//
0
Спасибо
Ответить
21 августа 2015 в 8:25
Рахат Торехан
Профиль
Благодарили: 0
Сообщений: 1
Рахат Торехан
Профиль
Благодарили: 0
Сообщений: 1
процент пример
0
Спасибо
Ответить
2 сентября 2015 в 17:11
Ответ для Рахат Торехан
Данек Кирпичев
Профиль
Благодарили: 0
Сообщений: 1
Данек Кирпичев
Профиль
Благодарили: 0
Сообщений: 1
50%-половина
0
Спасибо
Ответить
31 августа 2016 в 10:25
Ответ для Рахат Торехан
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
На ресурсе есть соответующая статья:
math-prosto.ru/index.php?page=pages/percent/percent1.php
0
Спасибо
Ответить
19 августа 2015 в 15:23
Дмитрий Алексеевич
Профиль
Благодарили: 0
Сообщений: 2
Дмитрий Алексеевич
Профиль
Благодарили: 0
Сообщений: 2
здрравствуйте вот я хочю из десятичную доробь перевести в процент что нужно делать
0
Спасибо
Ответить
20 августа 2015 в 9:15
Ответ для Дмитрий Алексеевич
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Здравствуй, Дмитрий.
Тебе необходимо умножить десятичную дробь на 100 и дописать знак «%».
Например: 0,75 = 0,75 · 100% = 75%
Более подробно ты можешь почитать об этом на странице «Проценты».
0
Спасибо
Ответить
Эта информация доступна зарегистрированным пользователям
В этом уроке мы научимся, зная дробь от числа, находить все число.
Также мы узнаем, как делать аналогичные действия для процентов, то есть по данному количеству процентов находить все число.
Потом применим полученные навыки для решения задач.
Сформулируем, в чем состоит задача нахождения числа по его дроби.
Имеется дробь; она говорит о том, какая часть от числа нам дана.
Имеется число, равное данной дробной части от искомого числа.
Мы уже умеем находить дробь от числа. Вспомним как это делать.
Эта информация доступна зарегистрированным пользователям
Чтобы найти дробь от числа нам нужно исходное число умножить на эту дробь, тогда получится какое-то значение, обозначающее дробь от числа.
В этой задаче было известно все число и то, какую дробную часть от него необходимо получить. Дробь от числа оставалась неизвестной.
В задаче этого урока дробь от числа нам уже известна, а все число, напротив, только предстоит найти.
Для его нахождения можно составить уравнение, аналогичное тому, которое было на картинке выше. Отличие будет только в том, какие переменные нам известны.
Решая это уравнение, вы переносите известный нам множитель, то есть дробь, в правую часть.
Как делить на дробь мы изучили в прошлом уроке. Напомним, что для этого надо домножить на взаимно обратное число к этой дроби.
Итак, вы получили выражение для неизвестного числа.
Сформулируем правило: чтобы найти дробь от числа необходимо разделить известную часть числа на дробь.
Эта информация доступна зарегистрированным пользователям
Пример 1
(mathbf{frac{3}{4}}) от числа равны 21-му, найдите исходное число.
Для решения необходимо разделить известную часть на дробь, то есть 21 разделить на (mathbf{frac{3}{4}})
(mathbf{21divfrac{3}{4}=21cdotfrac{4}{3}=frac{21cdot4}{3}=frac{7cdot4}{1}=28})
Пример 2
(mathbf{frac{2}{7}}) от числа равны 12, найдите исходное число.
Для решения надо разделить данную часть числа на данную дробь, то есть 12 разделить на (mathbf{frac{2}{7}})
(mathbf{12divfrac{2}{7}=12cdotfrac{7}{2}=frac{12cdot7}{2}=frac{6cdot7}{1}=42})
Пример 3
Далеко не всегда часть числа делится на числитель данной дроби; в таких случаях мы будем получать в ответе не целые числа, а дроби или смешанные числа.
(mathbf{frac{2}{3}}) от числа равны 11, найдите исходное число.
Во всем остальном решение ничем не будет отличаться- также разделим дробь от числа, равную (mathbf{frac{2}{3}}), на величину дроби, равную 11 и получим результат.
(mathbf{11divfrac{2}{3}=11cdotfrac{3}{2}=frac{11cdot3}{2}=frac{33}{2}=16frac{1}{2}})
Для получения ответа нам понадобилось выделить целую часть.
Важен еще один случай.
Никто не гарантирует, что данная нам часть числа сама по себе не будет являться дробью.
Такого случая не стоит пугаться, а стоит придерживаться алгоритма, а именно делить часть числа на то, какой дробью она является.
Пример 4
(mathbf{frac{5}{6}}) от числа равны (mathbf{frac{2}{3}}), найдите все число.
Для решения этого примера разделим (mathbf{frac{2}{3}})- часть числа, на (mathbf{frac{5}{6}})- дробь.
(mathbf{frac{2}{3}divfrac{5}{6}=frac{2}{3}cdotfrac{6}{5}=frac{2cdot6}{3cdot5}=frac{2cdot2}{5}=frac{4}{5}})
Все исходное число равняется (mathbf{frac{4}{5}})
Эта информация доступна зарегистрированным пользователям
Теперь представим, что дан какой-то определенный процент от числа и необходимо найти, от какого числа брали процент.
Вспомним, что процент- это способ записи десятичной дроби.
То есть, чтобы из процента получить десятичную дробь, которую он обозначает, надо величину процента разделить на 100.
Поэтому для решения такого рода задач надо преобразовать процент в десятичную дробь, а дальше сделать все то же самое: разделить число на эту дробь.
Пример 1
Известно, что зарплата работника увеличилась на 2 000 рублей или на 25 процентов. Какая зарплата у работника была изначально?
Решение:
Переведем проценты в дроби: (mathbf{25%=25div100=0.25})
Разделим число на дробь: (mathbf{2000div0.25=8000})
Ответ: изначально зарплата работника была 8000 рублей.
Сформулируем правило.
Чтобы найти число по проценту от него, надо перевести процент в десятичную дробь, а после разделить данную часть числа на полученную дробь.
Пример 2
Сказано, что 9% от числа равны 81. Необходимо найти все число.
Решение:
Первым действием переводим проценты в десятичную дробь.
(mathbf{9%=9div100=0.09})
Вторым действием делим данное число на эту дробь.
(mathbf{81div0.09=900})
Ответ: искомое число 900
Эта информация доступна зарегистрированным пользователям
Задачи, в которых фигурируют дроби от числа часто встречаются не только в школьных учебниках и задачниках, но и в реальной жизни, поэтому стоит уделить им особое внимание.
Сначала разберем некоторые из таких задач вместе, а дальше вы попробуете свои силы в самостоятельном решении задач.
Часть задач тривиальна, иными словами, их решение очевидно, достаточно лишь увидеть в них формулу, подставить в нее данные значения и получить результат.
Пример:
Айсберг возвышается над водой на (mathbf{frac{1}{11}}) своей высоты.
Капитан корабля заметил, что от воды до макушки айсберга по вертикали 16 метров.
Какова общая высота айсберга?
Решение:
В данном случае мы сразу можем сказать, что все число- это общая высота айсберга, дробь от числа- 16 (метров), а величина дроби- (mathbf{frac{1}{11}}).
Соответственно, по правилу, для получения ответа мы делим 16 на (mathbf{frac{1}{11}}) и получаем результат.
(mathbf{16divfrac{1}{11}=16cdot11=176}) (метр)- общая высота айсберга
Ответ: 176 (метров).
Некоторые задачи для своего решения требуют более глубокого анализа.
Пример:
Магазин продал (mathbf{frac{2}{3}}) пар новых кроссовок специальной партии, после чего на складе осталось 56 пар.
Какого размера была специальная партия?
Решение:
В данной задаче, если не вчитываться в условие, интуитивно хочется просто поделить 56 на (mathbf{frac{2}{3}}) и получить ответ, но ответ не будет правильным.
Если посмотреть внимательно, то 56 пар соответствуют оставшейся части партии, в то время как дробь (mathbf{frac{2}{3}}) описывает проданную часть.
Но мы пока не знаем общего количества пар и не можем сказать, какому числу соответствует (mathbf{frac{2}{3}})
Зато мы можем вычислить размер оставшейся части.
Если вся партия — это 1, и продано (mathbf{frac{2}{3}}), значит осталась (mathbf{frac{1}{3}}) товара.
Эта дробь соответствует 56 оставшимся парам.
Дальнейшие действия аналогичны рассмотренным в предыдущей задаче.
Теперь оформим решение:
1) (mathbf{1-frac{2}{3}=frac{1}{3}}) составляет оставшаяся часть от всего размера партии
2) (mathbf{56divfrac{1}{3}=56cdot3=168}) (пар) кроссовок всего было в партии
Ответ: 168 (пар).
Вам могут встретиться задачи и с более сложными условиями, все их разобрать невозможно, но главное:
- не давать себя запутать
- расписать, какой части какая дробь и какое число соответствует
- понять, где данных достаточно, чтобы узнать что- то новое
- и так постепенно продвигаться к ответу
Эта информация доступна зарегистрированным пользователям
Задачи математики часто диктуются другими науками, в том числе экономикой.
Существуют поднауки других наук, связанные с математикой. Примерами таких могут служить математическая физика, изучающая, как следует из названия, физические модели, а также математическая экономика, о которой мы вам сейчас расскажем.
Предметом изучения этой теории является математическое описание экономических объектов, явлений и процессов.
В самом деле, интересно применить мощнейший математический аппарат к таким насущным вопросам, как изменение цен и доходов, изменение предпочтений покупателей и пр.
Истоки математической экономики идут с XVII века. Тогда преподаватели германских университетов начали использовать новый стиль преподавания, который включал в себя статистику. Там, где появляется статистика, то есть множество чисел, появляется и математика, которая выявляет какие-то закономерности.
К примеру, расчет среднего дохода крестьян не является сложной задачей и сводится к вычислению среднего арифметического, но тоже является задачей математики.
В это же время группа английских ученых создала метод «численной аргументации государственной политики», который затрагивал темы налогов, сборов, таможенных пошлин, и прочие экономические процессы, в которых участвует государство.
К XIX веку появляется и развивается классическая школа политической экономики, чьим лицом принято считать Адама Смита.
Эта информация доступна зарегистрированным пользователям
Именно в этот период математика начала активно применяться в экономике.
В дальнейшем все большее количество математических инструментов переходило в экономику, а в наши дни на нее трудятся еще и информационные технологии.
Так что в наши дни великим экономистом может быть не тот, кто изначально учился на экономиста, а успешный математик или программист.
Для перевода обычной дроби в проценты надо знать, что такое процент и как он вычисляется. Слово «процент» своими корнями уходит в латинский язык, в котором «рrо сеntо» означало «за сто» или «на сотню», и приобрело значение сотой доли чего-либо. Так что процент — это одна сотая (1/100) или, в десятичных долях, 0,01.
Ну а дальше надо просто выражать любую обычную дробь в виде десятичной (пусть даже приблизительно, если точно разделить не получается) и полученный результат делить на указанные выше 0,01 — получим проценты.
Для наглядности — несколько примеров.
1/25 = 0,04 -> 0,04 : 0,01 = 4 -> значит 1/25 — это 4%;
3/7 ≈ 0,429 -> 0,429 : 0,01 = 42,9 -> 3/7 приблизительно составляют 42,9%;
5/8 = 0,625 -> 0,625 : 0,01 = 62,5 -> 5/8 — это 62,5%.
Процент – название, принятое во всем мире.
Превратить обыкновенную дробь в проценты и наоборот можно несколькими способами.
1 способ.
Мы умеем превращать десятичные дроби в проценты и наоборот.
1. 1/2 превращаем в проценты.
1/2 превратим в десятичную – 1/2 = 5/10 = 0,5.
Теперь 0,5 умножим на 100, получим – 50%.
2. 5/8 превращаем в проценты.
5/8 превратим в десятичную – 5/8 = 625/1000 = 0,625.
Теперь 0,625 умножим на 100, получим – 62,5%.
2 способ.
1. 1⁄2 превращаем в проценты.
1⁄2 превратим в десятичную, для этого 1 разделим на 2 = 0,5.
Теперь 0,5 умножим на 100, получим – 50%.
2. 15/32 превращаем в проценты.
15/32 превратим в десятичную, для этого 15 разделим на 32 = 0,46875.
Теперь 0,46875 умножим на 100, получим – 46,875%.
3 способ.
Способ 2 (см. выше), превратим в пропорцию.
5/8 превращаем в проценты.
Каждый из вас выберет более УДОБНЫЙ для себя способ.
Для превращения процентов в обыкновенную дробь, действуем наоборот.
1 способ.
1. 17,8% превратим в десятичную дробь.
17,8 делим на 100, получаем 17,8 : 100 = 0,178.
Теперь 178/1000 сократим дробь на 2, получим 89/500.
2. 96% превратим в десятичную дробь: 96/100.
Сокращаем на 4, получим 24/25.
2 способ.
20,125% превратим в обыкновенную дробь.
20,125 делим 100.
Получим 20,125/100.
Т.к. 20,125 не целое число, поэтому умножаем его на 1000. Тогда, чтобы дробь не изменилась, знаменатель – 100 тоже умножим на 1000.
Получим дробь — 20125/100000.
Сократим на 125 = 161/800.
Каждый выберет УДОБНЫЙ для себя способ.
Также можете воспользоваться памяткой в статье «Как перевести десятичную дробь в проценты?».