На чтение 7 мин Просмотров 25.4к.
Приведенную стоимость рассчитывают с целью определения сегодняшней цены инвестиций, доход от которых будет получен в будущем периоде. То есть, показатель отражает текущую стоимость активов с учетом доходности.
Содержание
- Понятие приведенной стоимости
- Зачем рассчитывают приведенную стоимость
- Расчет приведенной стоимости
- Формула для вычисления приведенной стоимости
- Пошаговый алгоритм расчета приведенной стоимости
- Пример вычисления приведенной стоимости
- Альтернативные методы расчета приведенной стоимости
- Расчет приведенной стоимости в Excel
Понятие приведенной стоимости
Приведенная стоимость (далее ПД) представляет собой значение доходности вложений на сегодняшний день. Если говорить простыми словами, приведенная стоимость – это объем денежных средств, которые инвестор получит в будущем периоде, переведенный в стоимость на сегодняшний день.
Кроме понятия «приведенная стоимость», в экономике существует такой термин, как «чистая приведенная стоимость» (далее ЧПД). ЧПД – это совокупность финансовых оборотов от вложений, переведенных в стоимость на момент проведения анализа.
Чистая приведенная стоимость отличается от ПД тем, что при определении первого показателя учитываются первоначальные финансовые вложения. То есть, сумма, которую компания инвестировала для получения дохода, отнимается из будущей стоимости актива, приведенной к значению на сегодняшний день.
Зачем рассчитывают приведенную стоимость
Приведенную стоимость рассчитывают с целью определения объема денежных средств, которые инвестор получит в будущем в стоимостной оценке на дату проведения анализа. Например, сегодня компания вложила 1 млн. рублей в развитие проекта. Неизвестно, сколько предприятие получит от реализации программы. Однако данное значение можно вычислить при помощи формулы расчета приведенной стоимости.
Как правило, в будущем денежные средства имеют совсем иную цену, в сравнении с днем сегодняшним. А особенностью вычисления приведенной стоимости считается тот факт, что анализ отражает сумму дохода в стоимости на сегодняшний день. Для этого будущий доход дисконтируется.
Расчет приведенной стоимости
Расчет приведенной стоимости значительно отличается от вычисления будущей доходности. Для того, чтобы вычислить приведенную стоимость, для начала, необходимо найти будущую доходность. Именно от этой суммы отталкивается аналитик, производящий анализ. Будущая стоимость в дальнейшем приводится к сегодняшнему значению путем дисконтирования.
Важно! Результат расчета приведенной стоимости показывает не сумму средств, которую инвестор получит в будущем, а объем финансов, необходимых для инвестирования.
То есть, вычисляя показатель ПС, сначала нужно понять, сколько инвестор хочет заработать от вложений. Затем можно приступать к расчетам при помощи арифметической формулы. Итог анализа – это и есть сумма, которой компания должна располагать на сегодняшний день, чтобы получить задуманный объем дохода.
Формула для вычисления приведенной стоимости
Анализ приведенной стоимости строится на расчете показателя. Его вычисление реализуется при помощи формул. Вид арифметического выражения напрямую зависит от метода начисления процентов: простого или сложного:
- Метод простых процентов предполагает расчет приведенной стоимости в традиционном порядке. Объем ожидаемых доходов дисконтируют в обычном порядке.
- Прием сложных процентов предполагает присоединение суммы процентов прошлого периода к общему объему финансов. Данную операцию в экономической теории называют капитализацией.
В связи с этим, каждый период денежный поток, поддающийся дисконтированию, должен быть разным:
| Метод определения приведенной стоимости | Формула | Расшифровка формулы |
| Простые проценты | БС / (1 + СД)н | БС – будущая стоимость;
СД – ставка дисконтирования; Н – число периодов инвестирования |
| Сложные проценты | БС / (1 + СДп)н*м | БС – будущая стоимость;
СДп – ставка дисконтирования за период; Н – число периодов инвестирования; М – число капитализаций в год |
Важно! Оценивая результаты расчета приведенной стоимости методом простых и сложных процентов, нужно опираться на наименьший результат. Это означает, что для получения одной и той же суммы дохода компании придется вложить меньше собственных средств.
Кроме ПС, можно определить показатель чистой приведенной стоимости. Вычисления проводятся также при помощи формулы:
(БС / (1 + СД)н) – ПИ,
где БС – будущая стоимость (предполагаемый доход);
СД – ставка дисконтирования (процентная ставка по договору);
Н – число периодов инвестирования;
ПИ – объем первоначальных вложений.
Таким образом, чистая приведенная стоимость — это ПС за исключением суммы инвестирования в проект.
Пошаговый алгоритм расчета приведенной стоимости
Для расчета ПС рекомендуется использовать пошаговую инструкцию, которая поможет избежать ошибок:
- Определяем период инвестирования. То есть, промежуток времени, через который инвестор планирует получить определенный доход.
- Вычисляем объем прибыли от инвестирования при условии соблюдения договора. Обычно показатель берется из документации по планированию.
- Находим ставку дисконтирования. Она определяется путем деления процентной ставки доходности на 100. В случае применения методики сложных процентов, определяем число случаев капитализации за 1 год.
- Рассчитываем приведенную стоимость путем замены буквенных выражений формулы на соответствующие числовые значения.
Сам процесс вычисления не сложен. Труднее исключить допущение ошибок, так как будущую доходность принято считать путем сложения денежных потоков.
Пример вычисления приведенной стоимости
Приведем пример вычисления приведенной стоимости на основании следующих условий. Компания планирует получить доход 1 млн. рублей от помещения денежных средств на депозит сроком на 5 лет. Банк предлагает два варианта начисления процентов: сложный (12% годовых) и простой (10% годовых). Перед заключением договора необходимо выбрать оптимальный метод. Для этого рассчитывается приведенная стоимость приемом сложных и простых процентов.
В первую очередь, определим приведенную стоимость методом простых процентов:
1 млн. руб. / (1 + 0,1)5 = 951465, 68 руб.
Таким образом, чтобы через 5 лет получить доход в размере 1 млн. рублей под 10% годовых, необходимо вложить 951465, 68 рублей. Теперь найдем приведенную стоимость методом сложных процентов. Допустим, проценты начисляются каждый месяц, пополнений не предусмотрено:
1 млн. руб. / (1 + 0,12 / 12)5 * 12 = 550375,73 руб.
Получается, что вложив 550375,73 руб. под сложные проценты 12% годовых, через 5 лет компания сможет иметь доход 1 млн. рублей Таким образом, гораздо выгоднее поместить средства на депозит под сложные проценты, так как при условии получения одинакового дохода за аналогичный промежуток времени необходимо вложить гораздо меньше средств.
Чтобы рассчитать чистую приведенную стоимость, из ожидаемого дохода нужно отнять рассчитанный показатель ПС:
- ЧПС методом простых процентов: 1 млн. руб. – 951465,68 руб. = 48534,32 рубля;
- ЧПС методом сложных процентов: 1 млн. руб. – 550375,73 = 449624,27 рублей.
Таки образом, можно сделать вывод о том, что чистая приведенная стоимость методом сложных процентов гораздо выше, чем при альтернативном варианте.
Альтернативные методы расчета приведенной стоимости
Альтернативным методом расчета приведенной стоимости является автоматизированный прием, основанный на использовании специализированных программ. Существует масса сервисов, которые помогают безошибочно рассчитать показатель. Если подобных инструментов нет, можно использовать стандартный Excel.
Excel – это программа, входящая в стандартный пакет Microsoft Office. Сервис наделен множествами функций, которые позволяют безошибочно проводить расчеты в автоматическом режиме по заданным параметрам. Главная сложность использования Excel заключается в неумении пользователей применять встроенные сервисы.
Основным достоинством расчета приведенной стоимости в Excel является то, что программа имеет функцию вычисления данного показателя. Поэтому нет необходимости вводить формулу. Достаточно выбрать инструмент и выделить участвующие в расчете ячейки.
Расчет приведенной стоимости в Excel
Вычисление приведенной стоимости в Excel производится при помощи встроенного инструмента. Нет необходимости вводить сложные формулы. Достаточно выбрать опцию и отразить ячейки, принимающие участие в анализе. Определение ПС в Excel имеет следующий алгоритм:
- создаем таблицу (начиная с 4 и далее строки), состоящую из трех столбцов – период, сумма периода и приведенная стоимость;
- в ячейках первого столбца отражаем последовательность периодов, в ячейках второго – сумму денежных потоков;
- третий столбец посвящен приведенной стоимости по временным промежуткам;
- чуть выше таблицы, например, в первой строке, прописываем значение ставки дисконтирования, во второй – итоговое значение приведенной стоимости, но ячейка, посвященная результату показателя, будет пустой;
- итоговую приведенную стоимость также необходимо отобразить в заключительной ячейке столбца показателя;
- после того, как все данные введены, можно приступать к указанию формул.
Положительной особенностью Excel является тот факт, что программа имеет встроенный инструмент для расчета приведенной стоимости. Достаточно найти функцию и выделить ячейки, необходимые для расчета. Сама формула для вычисления и результат сформируются автоматически.
Важно! Для расчета чистой приведенной стоимости отражение временных промежутков нужно начинать с нулевого года с отрицательным значением суммы инвестиций.
В дальнейшем, автоматически сформированную формулу нужно видоизменить, добавив сумму ячейки первоначальных вложений. Конечный результат ПС должен быть всегда положительным.
На чтение 14 мин Просмотров 40.9к. Опубликовано 07.09.2021
Расчет приведенной или дисконтированной стоимости может потребоваться в различных случаях. В том числе с 2022 года выполнять его придется всем бухгалтерам, у кого есть договоры аренды, признаваемой неоперационной, и лизинга. Постараемся рассказать простыми словами, что такое приведенная стоимость и как и зачем ее вычислять.
Содержание
- Дисконтирование простыми словами
- Зачем вообще это нужно
- Зачем берется банковская ставка
- Как определить ставку дисконтирования
- Как считать показатели для приведенной стоимости в Excel
- Функция ЧИСТВНДОХ
- Функция ЧИСТНЗ
- Дальнейшие вычисления для арендодателя
- Приведенная стоимость у арендатора
- Таблицы дисконтирования
- Бухгалтерские программы
Дисконтирование простыми словами
Рассмотрим пример
Банк сделал Васе персональное предложение по кредиту на сумму 200 тыс. руб. по ставке 10% годовых, сроком на год. Причем вернуть сумму с процентами можно всю сразу по завершении этого года.
Вася рассказал об этом своему другу Пете. И заметил, что все 200 тыс. руб. ему не нужны, но некоторой суммой он бы воспользовался. Петя предложил Васе взять весь кредит и ссудить часть суммы ему, а он, по прошествии года, вернет ее с такими же процентами.
Вася прикинул свои возможности и понял, что на возврат кредита он сможет набрать через год порядка 120 тыс. руб. Значит, вторую часть – еще 100 тысяч – должен к тому моменту вернуть Петя.
Сколько же нужно сегодня ссудить Пете под 10% годовых, чтобы через год он вернул 100 тысяч?
Считать нужно, исходя из формулы банковского (сложного) процента.
Например, общая сумма к возврату по Васиному кредиту:
S=200*(1+0,10)1 = 220
Степень 1 в формуле означает, что у кредита только один период выплаты – через год. Если бы срок был 2 года – в степень в формулу следовало бы поставить 2. И так далее.
Чтобы узнать, какая сумма, выданная под 10% годовых, через год превратиться в 220, нужно принять 200 тыс. руб. за Х и решить получившееся уравнение.
Х = 220/(1+0,10)1 = 200
А теперь Вася по той же методике посчитает, какая сумма превратится в 100 тыс. руб.
100/(1+0,10)1 = 90,91 тыс. руб.
Вася произвел дисконтирование и получил приведенную стоимость Петиной ссуды к возврату.
А мы запомним формулу дисконтирования:
К
ПС = ————-
(1+ r) t
ПС – приведенная (дисконтированная) стоимость
К – дисконтируемая сумма
r – процентная ставка
t – период кредитования
Зачем вообще это нужно
Продолжим пример
О том, что у Васи есть свободные средства, узнал Федя. Пришел к Васе и сказал:
— Инвестируй в мой бизнес свободные 100 тысяч и через 2 года я выплачу тебе 120 тысяч. Ты компенсируешь проценты, которые заплатишь банку по всему кредиту.
— Я подумаю, — сказал Вася и снова занялся подсчетами.
Потенциальный доход от вложения в бизнес Феди получится:
S=100*(1+ r)2 = 120
Решив уравнение, Вася выяснил, что на таких условиях он выдаст Феде деньги под 9,5% годовых. В то время как сам получит их под 10%. Да и воспользоваться ими сможет только через 2 года.
А вот, если Петя согласится взять еще 100 тысяч и вернуть через 2 года по ставке 10% годовых, то Вася получит:
S=100*(1+ 0,1)2 = 121 (побольше, чем от Феди).
В бытовых ситуациях, как у Васи из примера, можно обойтись базовыми формулами и не долгими подсчетами. Но что делать, если обсчитать надо большой и долгосрочный проект? Где много денежных потоков и двигаться они будут на отрезке времени длиннее, чем 1-2 года?
Есть два способа привести все потоки инвестпроекта к общему знаменателю, чтобы можно было сравнить разные проекты:
- Рассчитать будущую доходность от инвестируемой суммы и сравнить результат по разным проектам. Это будет процесс обратный дисконтированию и называется он компаундинг. (Примерно то, что сделал Вася, оценивая предложение Феди).
- Взять за основу прогнозные данные по получаемым в результате инвестирования денежным поступлениям и дисконтировать на текущий момент. Если, например, два проекта обещают поступления 1 миллион рублей через 3 года, но в результате приведения вложений оказалось, что в первый надо вложить 900 тысяч, а во второй 850, то второй проект можно рассматривать как более предпочтительный.
Зачем берется банковская ставка
Снова приведем пример
Костя выиграл в лотерею. После уплаты налогов у него остался 1 миллион рублей. Костя решил открыть свой бизнес – небольшое кафе. Арендовал помещение, купил оборудование, нанял персонал, сам за всем следил, практически в своем кафе поселился… Через год получил первую чистую прибыль – 50 тысяч рублей.
В то время как на момент открытия кафе можно было положить деньги в банк на депозит по 6% годовых. И получить по окончании года доход в 60 тысяч рублей, миллион обратно в свое распоряжение и все это не особо напрягаясь и с минимальными рисками.
С этим примером мы вплотную подошли к тому, для кого в идеале делается бухгалтерская отчетность по МСФО. А делается она для потенциальных инвесторов, которые, посмотрев на нее, должны принять решение: вложить свои деньги в эту компанию или проще отнести их в банк на депозит?
То есть инвестор, анализируя состояние дел компании по отчетности, подготовленной по принципам МСФО, оценивает выбор между двумя инвестиционными проектами – с компанией и с банком.
А, поскольку, в бухотчетности мы отражаем то, что есть именно на текущий момент, то для информативного отражения, например, расчетов по аренде и лизингу, мы пользуемся вторым способом, позволяющим сравнить разные проекты – дисконтированием. И из этих же соображений часто подставляем в формулу ставку дисконтирования – величину банковского процента.
Как определить ставку дисконтирования
Отметим, что в случае с долгосрочной арендой или лизингом у сторон сделки будет немного разный подход к оценке.
Арендатор (или лизингополучатель) должен показать, что для него взять объект в аренду или лизинг выгоднее, чем взять кредит и купить такой же объект. (Ну, или не выгоднее, и тогда отражение по приведенной стоимости даст убыток). Поэтому арендатор в качестве ставки для подстановки в формулу дисконтирования берет ставку, по которой он мог бы взять кредит на приобретение аналогичного объекта.
Если у арендатора уже есть подобные кредиты – можно опираться на ставку по ним. Если нет – нужно определять по какой ставке арендатор, на дату получения объекта, мог бы взять кредит с аналогичным сроком и обеспечением для приобретения примерно такого же.
Важно! В МСФО процесс выбора ставки дисконтирования гораздо более обусловлен и имеет несколько вариантов расчета. Причем выбранный вариант еще надо обосновать аудиторам. Российские ФСБУ, дублируя необходимость применения дисконтирования, пока не настолько усложнены и можно следовать общим предписаниям стандарта и логике.
У арендо- и лизингодателя ситуация больше похожа на ситуацию Кости, получившего миллион. У Кости заключен договор аренды, куплено оборудование и мебель. Как отбить обратно свой миллион, чтобы подумать, куда его дальше лучше вложить?
Продолжим пример
Костя нашел арендатора, который готов арендовать его кафе. Помещение, соответственно, пойдет в субаренду, а оборудование и мебель – в аренду от самого Кости. Договор заключен на 4 года, для упрощения расчетов примем, что арендатор рассчитывается сразу за год по 250 000 рублей. То есть, через 4 года Костя вернет свой миллион.
При этом у Кости уже есть вложения по объекту аренды:
480 000 – аренда (опять же, чтобы не перегружать пример, будем считать, что Костя оплатил всю сумму на 5 лет авансом);
280 000 – затраты на покупку оборудования и мебели;
40 000 – расходы на монтаж и обслуживание оборудования.
Итого можно определить стоимость инвестиционного вложения Кости – 800 тыс. руб.
То есть, следуя все тем же формулам, выполняется равенство:
800*(1+ r)4 = 1 000 000
Вот эта ставка r, при которой валовая стоимость инвестиции в аренду (будущий 1 миллион) равна справедливой стоимости вложений арендодателя (800 тысяч) и будет ставкой дисконтирования, которая нужна арендодателю. Зависящей от условий конкретного договора и позволяющей сравнивать его с другими подобными договорами.
Для полноты картины следует учесть, что оборудование и мебель, которые вернутся к Косте по окончании срока аренды, возможно, еще будут иметь какую-то ценность. Например, их можно будет продать как б/у, но еще годные к использованию. Поэтому, на практике, нужно эту ценность, называемую негарантированной ликвидационной стоимостью, оценить и добавить в равенство, приплюсовав к поступлениям от аренды.
Допустим, Костя договорился по окончании срока аренды помещения продать оптом находящееся в нем к тому моменту имущество (мебель и оборудование) за 50 000 рублей.
Тогда равенство для вычисления ставки дисконтирования примет вид
800*(1+ r)4 = 1 050 000 (1 000 000 + 50 000)
Отметим также, что на практике решить как уравнение подобное равенство для большого временного отрезка, а потом вычислить дисконтированные величины арендных платежей не так просто. Не всякий и не со всяким калькулятором справится. Поэтому далее мы поговорим о том, какие есть способы упростить расчеты.
Как считать показатели для приведенной стоимости в Excel
Традиционной палочкой-выручалочкой для бухгалтеров в случаях, когда надо дисконтировать, является Excel. В нем имеются функции как для расчета, например, ставки дисконтирования для арендодателя, так и для вычисления самих приведенных сумм.
Функция ЧИСТВНДОХ
С помощью этого средства как раз можно вычислить ставку внутренней доходности для арендодателя (лизингодателя).
Чтобы воспользоваться данным инструментом, нужно внести в лист Excel данные по датам и платежам договора. А в первой строке отразить величину инвестиционных вложений со знаком «-».
Возьмем данные из примера про сдачу в аренду Костиного кафе. Пусть кафе он передал арендатору 01.01.2022, а платит арендатор по истечении года. Для упрощения не станем учитывать негарантированную ликвидационную стоимость.
Далее ставим курсор в свободную ячейку и нажимаем на значок формул. Формула ЧИСТВНДОХ находится в разделе Финансовые. В англоязычном Excel она же называется XIRR.
Вносим данные для расчета, выделяя нужные области. На первое место ставим суммовые значения, на второе – даты
Далее жмем ОК и получаем ставку дисконтирования, с помощью которой арендодателю надо производить вычисления для отражения в отчетности договоров по ФСБУ 25/2018.
Важно!
Переписывать по датам обязательно нужно все платежи по условиям договора. Если у вас, к примеру, договор заключен на 5 лет с платежами ежемесячно, то придется заполнить 60 строк под каждый платеж.
А вот такие параметры как периодичность, аннуитетность – на точность вычислений не влияют. С помощью формулы можно рассчитывать ставку внутренней доходности и в случае, если платежи идут произвольно, и в случае, если их суммы не равные.
Функция ЧИСТНЗ
С помощью этой формулы, зная ставку дисконтирования, можно быстро вычислить чистую стоимость инвестиций в аренду на дату отражения в отчетности. Английская аббревиатура функции XNPV. Эта формула тоже больше подойдет для арендодателя (лизингодателя).
Для вычислений можно завести еще один столбец в табличке, которая получилась из платежей и их дат.
На момент передачи стоимость инвестиций принимаем равной справедливой стоимости вложений в объект аренды или лизинг. Скажем по секрету, что если объект ОС, передаваемый в аренду, учитывался с соблюдением правил приема на баланс, оценки и тестирования на обесценение, то его стоимость при передаче вполне можно считать справедливой.
А далее начинаем вычислять чистую стоимость инвестиций для каждого последнего дня года.
Важно! Если на дату, на которую определяется приведенная чистая стоимость инвестиций, приходится и дата платежа по договору, то сумму платежа нужно вычесть из значения, получившегося по формуле ЧИСТНЗ.
Выбираем значения, начиная от того, на дату которого считаем и далее до конца договора. Даты выбираем соответственно.
Вычитаем из получившегося по формуле значения сумму платежа по договору, чтобы получить справедливое значение на конец дня 31 декабря.
При наступлении следующей даты поступаем так же. Расчеты рекомендуется сохранить для каждого договора.
Дальнейшие вычисления для арендодателя
Используя полученные значения, арендодатель может определить величину дохода по процентам для отражения в учете по правилам ФСБУ 25/2018.
И получившаяся расчетная табличка целиком, на всякий случай.
Приведенная стоимость у арендатора
Описанный далее функционал больше подойдет арендаторам. Например, для вычисления приведенной стоимости платежей по договору.
В принципе, определив ставку дисконтирования, с помощью Excel можно производить расчеты и просто через формулы. Напомним, что значок степени в формуле Excel выставляется как комбинация «^число», например, чтобы возвести в 3-ю степень нужно ввести в формулу «^3».
Например, покажем, какая приведенная стоимость получится у платежей по договору у арендатора Костиного кафе. Допустим, что для покупки всего того, что он арендует у Кости, ему бы понадобилось взять кредит в банке по ставке 11,5% годовых.
Помним, что в данном случае дисконтируется каждый платеж. А t принимает значение количества периодов, оставшихся до платежа.
Если t выражено не в годах, а в более мелких периодах: кварталах или месяцах, то для подстановки в формулу дисконтирования нужно вычислить соответствующую периоду ставку исходя из годовой.
r = ((1 + годовая ставка/100)1/число периодов в году Х 100%
Например, при ежеквартальных платежах в степени будет 1/4
r = ((1 + годовая ставка/100)1/4 Х 100%
Также можно воспользоваться функцией ПС (приведенная стоимость, в английском PV). Помните, что она корректно работает только для единой процентной ставки и фиксированного размера периодического платежа.
Попробуем вычислить приведенную стоимость платежей по договору с помощью функции ПС
Ставка – указываем значение ставки за период платежа. Например, за квартал квартальную, рассчитав ее по предложенной выше формуле.
Кпер – количество периодов, за которые будут производятся платежи до конца договора. Мы вычисляем для всех платежей, поэтому ставим 4.
Плт – фиксированная сумма платежа за период. Если считаем поступления (например, от инвестиций), ставим значение с плюсом. Если считаем выплаты – ставим с минусом.
Бс – будущая стоимость. Желаемый остаток средств после завершения платежей. В данном случае он не нужен. Если ячейка не заполнена, программа автоматом считает 0.
Тип – характеристика выплаты: в начале периода – 1, в конце периода – 0. Если не заполнено, автоматически считается 0 (конец периода). У нас как раз конец периода, поэтому не заполняем.
Когда все внесено, нажимаем Ок.
Как видим, общая сумма дисконтированных платежей, рассчитанная по периодам, и сумма, полученная с помощью функции ПС одинаковы.
ЧПС – еще одна похожая функция. Удобна тем, что можно выбирать любые значения размера платежа из уже внесенных в таблицу.
Полученный результат совпадет с полученным по ПС и из сложения дисконтированных сумм каждого платежа.
Таблицы дисконтирования
Как вы, должно быть, уже успели заметить, дисконтированная сумма всегда меньше приводимой. И чем больше периодов дисконтирования, тем меньше итоговый результат.
То есть, можно сказать, что величина, которую мы дисконтируем, уменьшается в пропорции к количеству периодов и зависит от значения ставки.
Это давно подметили финансисты и высчитали закономерности для разных значений периодов и ставок. В результате мы можем пользоваться таблицами дисконтирования, которые есть в свободном доступе.
По вертикали в таких таблицах обычно идут периоды, а по горизонтали ставки. Единственный минус – ставки, как правило, выражены только в целых числах.
В остальном же работа с таблицами очень проста. Достаточно выбрать строку с нужным количеством периодов и столбец с нужным процентом, а на их пересечении будет ячейка с коэффициентом, на который надо умножить сумму, чтобы получить ее приведенное значение.
Вспомним Васю, который прикидывал, сколько денег дать Пете на 1 год под 10%, чтобы Петя вернул 100 тыс. руб.
Вася мог бы не проводить расчеты, а взять коэффициент из таблицы и умножить на него 100 000.
Бухгалтерские программы
На текущий момент (осень 2021 года) можно найти отдельно написанные программки, предназначенные для проведения вычислений, которые мы описали выше. Сделали их после появления ФСБУ 25/2018 для тех, кто хотел перейти на стандарт раньше установленного срока. Как вы понимаете, особенной популярностью это ПО не пользовалось. Даже то, которое коннектилось с 1С.
Что же касается 1С, то корректно работающий функционал для расчетов с приведенной стоимостью есть в 1С МСФО (там все настроено на МСФО и даже после внедрения ФСБУ логика расчетов все равно может отличаться) и в 1С Управление предприятием 2 (Бюджетирование лизинговых платежей).
Следует ожидать, что разработчики 1С отреагируют на необходимость ведения учета по ФСБУ 25/2018 и к 01.01.2022 появится необходимый функционал и в Бухгалтерии. Как только он появится – мы сразу же подготовим подробную инструкцию со скриншотами по работе с ним.
Автор материала:
Оксана Лим
Многие аспекты управления инвестициями часто связаны с активами, которые предполагают серию (т.е. последовательность) денежных потоков, возникающих с течением времени.
Денежные потоки могут быть очень неравномерными, относительно одинаковыми или равными.
Также денежные потоки могут возникать в течение относительно коротких периодов времени, более длительных периодов времени или даже растягиваться на неопределенный срок.
Далее мы обсудим, как найти текущую или приведенную стоимость (PV) серии денежных потоков.
Расчет текущей стоимости (PV) серии равных денежных потоков.
Начнем с обычного или простого аннуитета (англ. ‘ordinary annuity’). Напомним, что обычный аннуитет означает равные аннуитетные платежи, причем 1-й платеж начинается через 1 период (т.е. в конце текущего периода / начале следующего / при (t = 1)).
Всего простой аннуитет включает (N) платежей с первым взносом при (t = 1) и последним при (t = N).
Мы можем выразить текущую (приведенную) стоимость обычного аннуитета как совокупность текущей стоимости каждого отдельного аннуитетного платежа, как указано ниже:
(Формула 10)
( dst
PV = small {A over (1 + r)} + {A over (1 + r) ^ 2} + {A over (1 + r) ^ 3}
+ cdots + {A over (1 + r)^{N-1}} + {A over (1 + r)^N} )
где:
- (A) = сумма аннуитета,
- (r) = процентная ставка за период, соответствующая частоте выплаты аннуитета (например, годовой, ежеквартальный или ежемесячный),
- (N) = количество аннуитетных платежей.
Поскольку аннуитетный платеж (A) является константой в этом уравнении, его можно вывести за скобки. Таким образом, это выражение можно привести к следующей формуле:
( dstl PV = A left [1- dst {1 over (1 + r)^N} over r right] ) (Формула 11)
Точно так же, как и при вычислении будущей стоимости (FV) обычного аннуитета, мы находим приведенную стоимость (PV), умножая сумму аннуитета на фактор текущей стоимости аннуитета (англ. ‘present value annuity factor’) — он заключен в квадратные скобки в Формуле 11.
Пример расчета текущей (приведенной) стоимости обычного аннуитета.
Предположим, вы рассматриваете возможность покупки финансового актива, который обещает выплату в €1,000 каждый год в течение 5 лет с первым платежом через год.
Норма прибыли составляет 12% в год.
Сколько вы должны заплатить за этот актив?
Решение:
Чтобы узнать стоимость финансового актива, используйте Формулу (11) приведенной стоимости обычного аннуитета, со следующими данными:
(A) = €1,000
(r) = 12% = 0.12
(N) = 5
( begin{aligned} dst
PV &= A left [1- {1 over (1 + r)^N} over r right] \[1ex]
&= €1,000 left[ 1- {1over(1.12)^5} over 0.12 right] \[1ex]
&= €1,000 times (3.604776) = €3,604.78
end{aligned} )
Серия денежных потоков в размере €1,000 в год в течение 5 лет на текущую дату составляет €3,604.78 при дисконтировании по ставке 12%.
Необходимость отслеживания фактических календарных сроков приводит нас к специфическому типу аннуитета: авансовому аннуитету или аннуитету пренумерандо (англ. ‘annuity due’).
При авансовом аннуитете 1-ый платеж выполняется в текущую дату ((t) = 0). В общей сложности авансовый аннуитет включает (N) платежей.
На рисунке ниже представлена временная шкала авансового аннуитета из 4-х платежей в размере $100.

На рисунке мы можем видеть авансовый аннуитет с 4-мя периодами, состоящий из двух частей:
- единовременная сумма в размере $100 на текущую дату (при (t) = 0) и
- обычный аннуитет в размере $100 за период в течение 3-х периодов.
При ставке дисконтирования в 12% четыре денежных потока в размере 100$ в этом примере авансового аннуитета будут стоить $340,18.
Существует альтернативный способ расчета приведенной стоимости авансового аннуитета.
По сравнению с обычным аннуитетом каждый платеж авансового аннуитета дисконтируется на 1 период раньше.
Поэтому мы можем модифицировать Формулу 11, умножив правую часть уравнения на (1 + (r)):
(
defPVAD{{rm PV_{AD}}}
dstl
PVAD = A left[ 1-(1+r)^{-N} over r right] (1+r)
)
где ( PVAD ) — (PV) для авансового аннуитета
Выражение стоимости будущих денежных потоков в сегодняшнем эквиваленте дает нам удобный способ сравнения аннуитетов. Следующий пример иллюстрирует этот подход.
Пример расчета авансового аннуитета как суммы текущей стоимости единичного денежного потока и обычного аннуитета.
Вы выходите на пенсию сегодня и должны либо получить свое пенсионное пособие в виде паушальной суммы (т.е. единовременной выплаты всех пенсионных накоплений), либо в виде аннуитета.
Сотрудник вашей компании, занимающийся выплатой пособий, предлагает вам две альтернативы:
- немедленную единовременную выплату в размере $2 млн. или
- аннуитет с 20 платежами в размере $200 000 в год с первым платежом от текущей даты.
Процентная ставка в вашем банке составляет 7% годовых с ежегодным начислением процентов.
Какой вариант обеспечивает большую текущую стоимость? (Игнорируйте любые налоговые различия между двумя вариантами.)
Решение:
Чтобы сравнить эти два варианта, необходимо найти текущую стоимость каждого из них в момент времени
(t) = 0 и выбрать наибольшее значение.
Приведенная стоимость первого варианта составляет $2 млн., т.е. первый вариант уже выражен в сегодняшнем эквиваленте.
Второй вариант — аннуитет. Поскольку первый платеж происходит при (t) = 0, вы можете разделить этот аннуитет на две части:
- немедленную выплату $200,000 от текущей даты ((t) = 0) и
- обычный аннуитет в размере $200,000 в год в течение 19 лет.
Чтобы рассчитать этот аннуитет, вам нужно найти приведенную стоимость обычного аннуитета, используя Формулу 11, а затем добавить к нему $200,000.
(A) = $200,000
(r) = 7% = 0.07
(N) = 19
( begin{aligned} dst
PV &= A left [1- {1 over (1 + r)^N} over r right] \[1ex]
&= $200,000 left[ 1- {1over(1.07)^{19}} over 0.07 right] \[1ex]
&= $200,000(0.335595) =$2,067,119.05
end{aligned} )
19 платежей в размере $200 000 имеют текущую (приведенную) стоимость в размере $2,067,119.05. Добавив к этой сумме первоначальный платеж в размере $200,000, мы обнаружим, что общая стоимость аннуитета составляет $2,267,119.05.
Текущая стоимость аннуитета больше, чем единовременная альтернатива в размере $2 млн.
Теперь рассмотрим другой пример, подтверждающий эквивалентность текущей и будущей стоимости.
Пример расчета прогнозируемой приведенной стоимости обычного аннуитета.
Менеджер немецкого пенсионного фонда ожидает, что пенсионерам будут выплачиваться пособия в размере €1 млн. в год. Пенсионные выплаты начнут осуществляться через 10 лет от текущей даты, при (t) = 10.
После того, как пособия начнут выплачиваться, эти выплаты продлятся до (t) = 39, что составляет в общей сложности 30 платежей.
Какова текущая (приведенная) стоимость пенсионного обязательства, если соответствующая годовая ставка дисконтирования для обязательств по пенсионной программе составляет 5% годовых, начисляемых ежегодно?
Решение:
Эта задача связана с аннуитетом, первый платеж по которому наступает через 10 лет, при (t) = 10.
При этом, на момент (t) = 9 мы имеем обычный аннуитет с 30 платежами. Мы можем вычислить приведенную стоимость (PV) этого аннуитета с помощью Формулы 11, а затем посмотреть на нее на временной шкале.
(A) = €1,000,000
(r) = 5% = 0.05
(N) = 30
( begin{aligned} dst
PV &= A left [1- {1 over (1 + r)^N} over r right] \[1ex]
&= €1,000,000 left[ 1- {1over(1.05)^{30}} over 0.05 right] \[1ex]
&= €1,000,000(15.372451) = €15,372,451.03
end{aligned} )
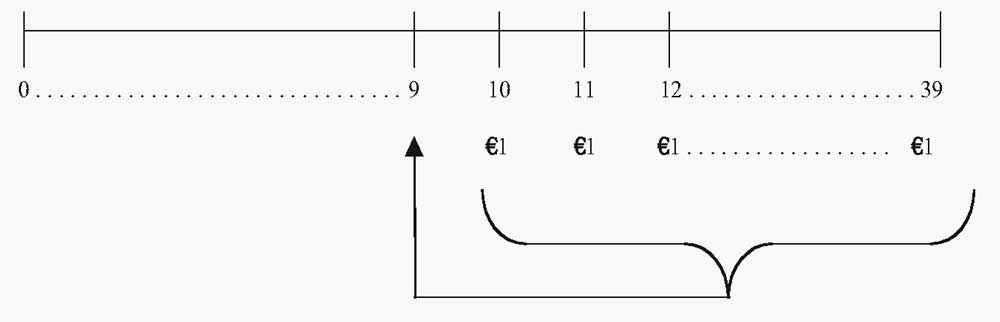
На временной шкале мы отразили пенсионные выплаты в размере €1 млн., занимающие отрезок от (t) = 10 до (t) = 39.
Фигурная скобка и стрелка обозначают процесс нахождения текущей стоимости аннуитета, дисконтированной к моменту времени (t) = 9.
Текущая стоимость (PV) пенсионных выплат по состоянию на (t) = 9 составляет €15,372,451.03.
Далее задача заключается в том, чтобы найти приведенную стоимость на текущую дату (при (t) = 0). Теперь мы можем полагаться на эквивалентность текущей стоимости и будущей стоимости
Как показано на временной лини, мы можем рассматривать сумму при (t) = 9 в качестве будущей стоимости с точки зрения (t) = 0.
Мы вычислим приведенную стоимость (PV) при (t) = 0 следующим образом:
(FV_N) = €15,372,451.03 (приведенная стоимость при (t) = 9)
(N) = 9
(r) = 5% = 0.05
( begin{aligned}
PV &= FV_N times (1 + r)^{-N} \[1ex]
&= €15,372,451.03 times (1.05)^{-9} \[1ex]
&= €15,372,451.03 times (0.644609) = €9,909,219.00
end{aligned} )
Приведенная стоимость на текущую дату (при (t) = 0) пенсионного обязательства составляет €9,909,219.00.
Приведенный пример иллюстрирует три процедуры:
- определение текущей (PV) или будущей стоимости (FV) любой последовательности денежных потоков;
- признание эквивалентности текущей и будущей стоимости; а также
- отслеживание фактического календарного времени на временной шкале при вычислениях, связанных с временной стоимостью денег (TVM).
Как вычислять приведенную стоимость (PV) бесконечной серии равных денежных потоков — бессрочный аннуитет?
Рассмотрим случай обычного аннуитета, который длится бесконечно. Такой обычный аннуитет называется бессрочным аннуитетом или перпетуитетом или вечной рентой (англ. ‘perpetuity’ или ‘perpetual annuity’).
Чтобы получить формулу для текущей стоимости перпетуитета, мы можем модифицировать Формулу 10, чтобы учесть бесконечную последовательность денежных потоков:
( dstl PV = A sum _{t = 1} ^{infty} left[ 1 over (1 + r)^t right] ) (Формула 12)
Пока процентные ставки положительны, сумма факторов текущей стоимости позволяет получить формулу в следующем виде:
( dstl PV = A / r ) (Формула 13)
Чтобы понять смысл этого преобразования, обратите внимание на Формулу 11 приведенной стоимости обычного аннуитета.
Поскольку (N) (количество периодов в аннуитете) переходит в бесконечность, выражение ( 1 / (1 + r)^N ) приближается к 0, а Формула 11 упрощается до Формулы 13.
Эта формула потребуется, когда мы будем оценивать дивиденды по акциям, поскольку акции не имеют предопределенного срока действия.
Акция, выплачивающая постоянные дивиденды, аналогична бессрочному аннуитету.
При первом платеже через год от текущей даты, перпетуитет в размере $10 в год при 20%-ой норме прибыли имеет текущую стоимость в размере $10 / 0,2 = $50 долларов.
Формула 13 справедлива только для бессрочного аннуитета с равными платежами.
В примере выше первый платеж произошел при (t = 1); поэтому мы вычисляем текущую стоимость при (t = 0).
Некоторые финансовые активы также соответствуют концепции бессрочного аннуитета. Определенные государственные облигации и привилегированные акции являются типичными примерами финансовых активов, которые обеспечивают равные выплаты в течение неопределенного срока.
Пример расчета текущей стоимости (PV) перпетуитета.
Британское правительство когда-то выпускало форму ценных бумаг, называемых «консолями» (англ. ‘consol bond’). Это — бессрочные облигации (англ. ‘perpetual bond’), которые обеспечивают равные денежные выплаты в течение неограниченного срока.
Если бессрочная облигация приносит £100 в год в течение неограниченного срока, сколько бы она стоила сегодня, если норма прибыли составляет 5%?
Решение:
Чтобы ответить на этот вопрос, мы можем использовать Формулу 13 со следующими данными:
(A) = £100
(r) = 5% = 0.05
( PV = A/r = £100/0.05 = £2,000 )
Облигация будет стоить £2 000.
Приведенная стоимость на момент времени, отличный от текущей даты (t = 0).
На практике финансовым аналитикам часто приходится находить текущие значения стоимости, на различные моменты времени, отличные от (t = 0).
Если мы рассчитаем перпетуитет, начинающийся с платежа в размере $100 на 2-й год, то мы получим:
( PV_1 = $100 / 0,05 = $2,000 ) при 5%-й ставке
Кроме того, мы можем рассчитать PV на текущую дату как:
( PV_0 = $2,000 / 1.05 = $1,904.76 )
Рассмотрим аналогичную ситуацию, в которой денежные потоки в размере $6 в год начинаются в конце 4-го года и продолжаются в конце каждого года после этого с последним потоком денежных средств в конце 10-го года.
По состоянию на конец 3-го года мы сталкиваемся с типичным 7-летним обычным аннуитетом. Мы можем найти текущую стоимость аннуитета на конец 3-го года, а затем привести эту стоимость к текущей дате.
При процентной ставке 5% денежные потоки в размере $6 в год, начинающиеся в конце 4-го года, будут стоить $34,72 на конец 3-го года ((t) = 3) и $29,99 на текущую дату ((t) = 0).
Следующий пример иллюстрирует важную концепцию, согласно которой начинающийся в будущем аннуитет или перпетуитет может быть выражен в текущей стоимости за один период до первого платежа. Эта стоимость может быть приведена к текущей стоимости на сегодняшнюю дату.
Пример расчета приведенной стоимости (PV) бессрочного аннуитета (перпетуитета) с отсроченной первой выплатой.
Рассмотрим перпетуитет с равными платежами в £100 в год, с первой выплатой, начинающейся при (t = 5).
Какова будет его текущая (приведенная) стоимость на сегодняшнюю дату (при t = 0), при 5-процентной ставке дисконтирования?
Решение:
Во-первых, мы находим приведенную стоимость перпетуитета при (t = 4), а затем дисконтируем эту сумму к текущей дате (t = 0).
Напомним, что у перпетуитета и обычного аннуитета первый платеж осуществляется на конец первого периода, что объясняет индекс (t = 4) для нашего расчета приведенной стоимости).
1. Находим текущую стоимость перпетуитета при (t = 4):
(A) = £100
(r) = 5% = 0.05
( PV = A/r = £100/0.05 = £2,000 )
2. Находим текущую стоимость будущего значения при
(t = 4).
С точки зрения сегодняшней даты (t = 0) текущую стоимость в £2,000 можно считать будущей стоимостью.
Теперь нам нужно найти текущую стоимость £2,000 при
(t = 0):
(FV_N ) = £2,000 (текущая стоимость при (t = 4))
(r) = 5% = 0.05
(N) = 4
( begin{aligned}
PV &= FV_N (1 + r)^{-N} \[1ex]
&= £2,000 (1.05)^{-4} = £2,000 (0.822702) = £1,645.40
end{aligned} )
Приведенная стоимость перпетуитета на текущую дату составляет £1,645.40.
Как обсуждалось ранее, аннуитет представляет собой серию платежей с фиксированной (одинаковой) суммой в течение определенного количества периодов.
В ситуации с перпетуитетом число периодов бесконечно. В этом случае мы предоставляем бессрочное обязательство производить платежи, и эти платежи имеют одинаковую сумму. Тем не менее, первая (1) часть перпетуитета отсрочена и выплачивается при (t) = 5; после этого платежи продолжаются бесконечно.
Выплаты по второй (2) части перпетуитета компенсируют смещение 1-го платежа первой (1) части перпетуитета к (t) = 5.
Благодаря этому перпетуитет с отсроченной 1-й выплатой (до (t) = 5) обеспечивает выплаты при (t) = 1, 2, 3 и 4. Выплаты за эти 4 периода точно соответствуют определению обычного аннуитета с четырьмя платежами.
Таким образом, мы можем представить обычный аннуитет как разницу между двумя перпетуитетами с равными платежами, но с разными датами начала выплат.
Следующий пример иллюстрирует этот результат.
Пример расчета приведенной стоимости обычного аннуитета как разницы между текущей стоимостью (PV) и прогнозируемым (отсроченным) перпетуитетом.
С учетом 5%-ой ставки дисконтирования, найдите текущую (приведенную) стоимость 4-летнего обычного аннуитета в размере £100 в год, с выплатами начиная с 1-го года, в качестве разницы между следующими двумя перпетуитетами:
- Перпетуитет 1 на £100 в год, начиная с 1-го года
(первый платеж при (t) = 1). - Перпетуитет 2 на £100 в год, начиная с 5-го года
(первый платеж при (t) = 5).
Решение:
Если мы вычтем Перпетуитет 2 из Перпетуитета 1, мы получим обычный аннуитет в размере £100 за 4 года (платежи при (t) = 1, 2, 3, 4).
Вычитая текущую стоимость Перпетуитета 2 из Перпетуитета 1, мы придем к текущей (приведенной) стоимости четырехлетнего обычного аннуитета:
(PV_0) (Перпетуитет 1) = £100 / 0.05 = £2,000
(PV_4) (Перпетуитет 2) = £100 / 0.05 = £2,000
(PV_0) (Перпетуитет 2) = £2,000 / (1.05)4 = £1,645.40
(PV_0) (Аннуитет) =
= (PV_0) (Перпетуитет 1) — (PV_0) (Перпетуитет 2)
= £2,000 — £1,645.40 = £354.60
Текущая стоимость 4-летнего обычного аннуитета равна £2,000 — £1,645.40 = £354.60.
Как вычислять приведенную стоимость (PV) для серии неравных денежных потоков?
Когда мы имеем неравные денежные потоки, мы должны сначала найти приведенную стоимость (PV) каждого отдельного денежного потока, а затем суммировать соответствующие значения PV.
Для серии (последовательности) с большим количеством денежных потоков мы обычно используем электронную таблицу.
В таблице ниже приведена последовательность денежных потоков с
- временными периодами в 1-м столбце,
- денежными потоками во 2-м столбце и
- текущей стоимостью (PV) каждого денежного потока в 3-м столбце.
В итоговой строке таблице показана сумма приведенных значений для всей серии денежных потоков.
|
Период |
Денежный поток ($) |
PV при t=0 |
|
|---|---|---|---|
|
1 |
1,000 |
$1,000(1.05)-1 = |
$952.38 |
|
2 |
2,000 |
$2,000(1.05)-2 = |
$1,814.06 |
|
3 |
4,000 |
$4,000(1.05)-3 = |
$3,455.35 |
|
4 |
5,000 |
$5,000(1.05)-4 = |
$4,113.51 |
|
5 |
6,000 |
$6,000(1.05)-5 = |
$4,701.16 |
|
Сумма = |
$15,036.46 |
Мы могли бы рассчитать будущую стоимость (FV) серии этих денежных потоков, вычислив ее по отдельности для каждого потока с использованием формулы расчета будущей стоимости.
Однако мы уже знаем текущую стоимость этой серии, поэтому мы можем легко применить принцип временной эквивалентности для всей суммы денежных потоков сразу.
Будущая стоимость серии денежных потоков составляет $19,190.76 и эквивалентна единовременному денежному потоку размере $15,036.46, с приведением к периоду (t) = 5:
(PV) = $15,036.46
(N) = 5
(r) = 5% = 0.05
( begin{aligned}
FV_N &= PV (1 + r)^N \
&= $15,036.46 (1.05)^5 \
&= $15,036.46 (1.276282) = $19,190.76
end{aligned} )
Здравствуйте, уважаемы читатели проекта Тюлягин! В сегодняшней статье мы поговорим с вами о таком понятии как приведенная стоимость или более просто и доступно — текущая стоимость. В стать вы узнаете что такое и в чем основная суть приведенной стоимости, как инфляция влияет на покупательную способность денег и причем тут приведенная стоимость. Наконец, в статье изложена формула и расчет приведенной стоимости с примерами. Об этом и многом другом, связанном с текущей стоимостью, далее в сегодняшней статье.
Содержание статьи:
- Что такое приведенная стоимость (PV)?
- Суть приведенной стоимости (PV)
- Инфляция и покупательная способность
- Ставка дисконтирования для определения приведенной стоимости
- Формула PV и расчет
- Будущая стоимость против текущей стоимости
- Критика текущей стоимости
- Пример приведенной стоимости
- Популярные вопросы о приведенной стоимости
- Резюме
Приведенная стоимость (PV), (также часто называемая как текущая стоимость или дисконтированная стоимость) — это текущая стоимость будущей суммы денег или потока денежных средств при заданной норме прибыли. Будущие денежные потоки дисконтируются по ставке дисконтирования, и чем выше ставка дисконтирования, тем ниже приведенная стоимость будущих денежных потоков. Определение подходящей ставки дисконтирования является ключом к правильной оценке будущих денежных потоков, будь то прибыль или долговые обязательства.
Суть приведенной стоимости (PV)
Приведенная стоимость — это концепция, согласно которой сумма денег сегодня будет стоить больше, чем та же сумма в будущем. Другими словами, деньги, полученные в будущем, не стоят столько, сколько эквивалентная сумма, полученная сегодня.
Получение 100 000 рублей сегодня будет стоить более 100 000 рублей через пять лет. Почему? Инвестор может вложить 100 000 рублей сегодня и предположительно получить доход в течение следующих пяти лет. Приведенная стоимость учитывает любую процентную ставку, которую может принести инвестиция.
Например, если инвестор получает 100 000 рублей сегодня и может получать доходность 5% в год, то сегодняшняя 100 000 рублей, безусловно, стоит больше, чем получение 100 000 рублей через пять лет. Если инвестор ждал пять лет, чтобы получить 100 000 рублей, возникли бы альтернативные издержки или инвестор потерял бы доходность за пять лет.
Инфляция и покупательная способность
Инфляция — это процесс, при котором цены на товары и услуги со временем растут. Если вы получите деньги сегодня, вы сможете покупать товары по сегодняшним ценам. Предположительно, инфляция вызовет рост цен на товары в будущем, что снизит покупательную способность ваших денег.
Можно ожидать, что деньги, не потраченные сегодня, потеряют ценность в будущем из-за некоторой подразумеваемой годовой ставки, которой может быть инфляция или норма прибыли, если деньги были вложены. Формула приведенной стоимости дисконтирует будущую стоимость к сегодняшним рублям с учетом предполагаемой годовой ставки либо из инфляции, либо из нормы прибыли, которая могла бы быть получена, если бы сумма была инвестирована.
Ставка дисконтирования для определения приведенной стоимости
Ставка дисконтирования — это норма доходности инвестиций, которая применяется при расчете приведенной стоимости. Другими словами, ставка дисконтирования была бы упущенной нормой прибыли, если бы инвестор решил принять сумму в будущем по сравнению с той же суммой сегодня. Ставка дисконтирования, выбранная для расчета приведенной стоимости, очень субъективна, потому что это ожидаемая норма прибыли, которую вы получили бы, если бы вы вложили сегодняшние доллары в течение определенного периода времени.
Во многих случаях определяется безрисковая ставка доходности, которая используется в качестве ставки дисконтирования, которую часто называют пороговой ставкой. Ставка представляет собой норму прибыли, которую необходимо получить от инвестиций или проекта, чтобы их можно было продолжать. Ставка казначейских облигаций США (или государственных облигаций других стран, в России это ОФЗ) часто используется в качестве безрисковой ставки, поскольку казначейские облигации поддерживаются правительством США. Так, например, если двухлетние трежерис дают 2% годовых или доходности, инвестиции должны приносить как минимум более 2%, чтобы оправдать риск.
Ставка дисконтирования — это сумма временной стоимости и соответствующей процентной ставки, которая математически увеличивает будущую стоимость в номинальном или абсолютном выражении. И наоборот, ставка дисконтирования используется для расчета будущей стоимости с точки зрения приведенной стоимости, позволяя кредитору рассчитаться по справедливой сумме любых будущих доходов или обязательств по отношению к приведенной стоимости капитала. Слово «дисконт» относится к будущей стоимости, дисконтируемой до текущей стоимости.
Расчет дисконтированной или приведенной стоимости чрезвычайно важен во многих финансовых расчетах. Например, чистая приведенная стоимость, доходность облигаций и пенсионные обязательства зависят от дисконтированной или приведенной стоимости. Изучение того, как использовать финансовый калькулятор для расчета приведенной стоимости, может помочь вам решить, следует ли вам принимать такие предложения, как скидка наличными, 0% финансирование при покупке автомобиля или выплаты по ипотеке.
Формула приведенной стоимости PV и расчет
Приведенная (текущая) стоимость (PV) = FV / (1 + r) ^ n
где:
FV — Будущая стоимость
r — Норма прибыли, ставка дисконтирования
n — Количество периодов
- Введите сумму, которую вы ожидаете получить в будущем, в числитель формулы.
- Определите процентную ставку, которую вы ожидаете получить в период между настоящим моментом и будущим, и укажите ставку в виде десятичной дроби вместо «r» в знаменателе.
- Введите период времени как показатель степени «n» в знаменателе. Итак, если вы хотите рассчитать приведенную стоимость суммы, которую ожидаете получить через три года, вы должны подставить цифру три вместо «n» в знаменателе.
- В Интернете существует ряд онлайн-калькуляторов для удобного и быстрого расчета приведенной стоимости. Например этот.
Будущая стоимость и приведенная (текущая) стоимость
Сравнение текущей стоимости (PV) с будущей стоимостью (FV) лучше всего иллюстрирует принцип временной стоимости денег и необходимость взимания или выплаты дополнительных процентных ставок, основанных на риске. Проще говоря, с течением времени деньги сегодня стоят больше, чем те же деньги завтра. Будущая стоимость может относиться к будущим денежным потокам от инвестирования сегодняшних денег или будущим платежам, необходимым для возврата денег, взятых сегодня в долг.
Будущая стоимость (FV) — это стоимость текущего актива на определенную дату в будущем, основанную на предполагаемых темпах роста. Уравнение FV предполагает постоянные темпы роста и единовременный авансовый платеж, который остается нетронутым на протяжении всего периода инвестирования. Расчет справедливой стоимости позволяет инвесторам с разной степенью точности прогнозировать сумму прибыли, которую можно получить от различных инвестиций.
Приведенная стоимость (PV) — это текущая стоимость будущей суммы денег или потока денежных средств при заданной норме прибыли. Приведенная стоимость принимает будущую стоимость и применяет ставку дисконтирования или процентную ставку, которая может быть получена в случае инвестирования. Будущая стоимость говорит вам, сколько будет стоить инвестиция в будущем, а текущая стоимость говорит вам, сколько вам нужно в сегодняшних рублях, чтобы заработать определенную сумму в будущем.
Критика текущей стоимости
Как указывалось ранее, расчет приведенной стоимости предполагает допущение, что доходность средств может быть получена за определенный период времени. В приведенном обсуждении мы рассмотрели одну инвестицию в течение одного года. Однако, если компания решает продолжить серию проектов, которые имеют разную норму доходности для каждого года и каждого проекта, приведенная стоимость становится менее определенной, если эти ожидаемые нормы доходности нереалистичны. Важно учитывать, что при принятии любого инвестиционного решения не гарантируется процентная ставка, а инфляция может снизить доходность инвестиций.
Пример приведенной стоимости
Допустим, у вас есть выбор: получать 200 000 рублей сегодня и 3% годовых или 220 000 рублей через год. Какой вариант лучше?
- Используя формулу приведенной стоимости, расчет составит 220 000 рублей / (1 +. 03) 1 = 213 592 рублей
- PV = 213 592 рублей, или минимальная сумма, которую вам нужно будет заплатить сегодня, чтобы через год получить 220 000 рублей. Другими словами, если бы вам заплатили 200 000 рублей сегодня и исходя из процентной ставки 3%, этой суммы было бы недостаточно, чтобы дать вам 220 000 рублей через год.
- В качестве альтернативы вы можете рассчитать будущую стоимость 200 000 рублей сегодня через год: 200 000 x 1,03 = 206 000 рублей.
Приведенная стоимость обеспечивает основу для оценки справедливости любых будущих финансовых выгод или обязательств. Например, будущий возврат денежных средств, дисконтированный до приведенной стоимости, может стоить или не стоить потенциально более высокой покупной цены. Тот же финансовый расчет применяется к 0% финансированию при покупке автомобиля.
Выплата некоторого процента по более низкой цене может оказаться более выгодной для покупателя, чем уплата нулевого процента по более высокой цене. Выплата ипотеки сейчас в обмен на более низкие выплаты по ипотеке в будущем имеет смысл только в том случае, если приведенная стоимость будущих сбережений по ипотеке больше, чем выплаченные сегодня ипотечные выплаты.
Популярные вопросы о приведенной стоимости
Как вы рассчитываете приведенную стоимость?
Приведенная стоимость рассчитывается путем дисконтирования будущих денежных потоков, ожидаемых от инвестиций, до настоящего времени. Для этого инвестору нужны три ключевых точки данных: ожидаемые денежные потоки, количество лет, в течение которых денежные потоки будут выплачиваться, и их ставка дисконтирования. Ставка дисконтирования является очень важным фактором, влияющим на приведенную стоимость, при этом более высокие ставки дисконтирования приводят к более низкой приведенной стоимости, и наоборот. Используя эти переменные, инвесторы могут рассчитать приведенную стоимость по формуле:
PV = FV / (1 + r) ^ n
где:
PV — Текущая (приведенная) стоимость
FV — Будущая стоимость
r — Норма прибыли, ставка дисконтирования
n — Количество периодов
Какие есть примеры приведенной стоимости?
Для иллюстрации рассмотрим сценарий, в котором вы ожидаете получить единовременную выплату в размере 50 000 рублей через пять лет. Если ставка дисконтирования составляет 8,25%, вы хотите знать, сколько будет стоить этот платеж сегодня, поэтому вы рассчитываете PV = 50 000 рублей / (1,0825) ^ 5 = 33 638 рублей.
Почему важна текущая (приведенная) стоимость?
Приведенная стоимость важна, потому что она позволяет инвесторам судить о том, является ли цена, которую они платят за инвестиции, уместной. Подобные расчеты приведенной стоимости играют решающую роль в таких областях, как инвестиционный анализ, управление рисками и финансовое планирование.
Резюме
- Приведенная стоимость означает, что сумма денег сегодня стоит больше, чем такая же сумма в будущем.
- Другими словами, приведенная стоимость показывает, что деньги, полученные в будущем, не стоят столько, сколько эквивалентная сумма, полученная сегодня.
- Неизрасходованные сегодня деньги могут потерять ценность в будущем из-за предполагаемой годовой ставки из-за инфляции или нормы прибыли, если деньги были вложены.
- Расчет приведенной стоимости предполагает допущение, что доходность средств может быть получена за период.
А на этом сегодня все про приведенную стоимость. Надеюсь статья оказалась для вас полезной. Делитесь статьей в социальных сетях и мессенджерах и добавляйте сайт в закладки. Успехов и до новых встреч на страницах проекта Тюлягин!
Чистая приведенная стоимость (NPV), наиболее часто используемая для оценки прибыльности проекта, рассчитывается как разница между приведенной стоимостью притока денежных средств и приведенной стоимостью оттока денежных средств за период реализации проекта. Если разница положительная, то это прибыльный проект, а если отрицательная, то не достойный.
Оглавление
- Чистая приведенная стоимость (NPV) Определение
- Формула чистой приведенной стоимости (NPV)
- Объяснение формулы чистой приведенной стоимости
- Примеры
- Использование NPV для оценки — пример использования Alibaba
- Использование и актуальность
- Калькулятор чистой приведенной стоимости
- Чистая приведенная стоимость в Excel (с шаблоном Excel)
- Видео о чистой приведенной стоимости
- Рекомендуемые статьи:
Формула чистой приведенной стоимости (NPV)
NPVt=1 к T = ∑Xt / [(1+R)t – X0]
Вот формула чистой приведенной стоимости (при равномерном поступлении денежных средств):
NPVt=1 к T = ∑ Xt/(1 + R)t – Xo
Где,
- Xt = общий приток денежных средств за период t
- Xo = чистые первоначальные инвестиционные расходы
- R = ставка дисконтирования, наконец
- t = общее количество периодов времени
Формула чистой приведенной стоимости (при неравномерном поступлении денежных средств):
чистая приведенная стоимость = [Ci1/ (1+r)1 + Ci2/(1+r)2 + Ci3/(1+r)3 + …] — Ксо
Где,
- R — указанная норма доходности за период;
- Ci1 – консолидированное поступление денежных средств за первый период;
- Ci2 – консолидированное поступление денежных средств за второй период;
- Ci3 — консолидированное поступление денежных средств за третий период и т. д.
Объяснение формулы чистой приведенной стоимости
Формула NPV состоит из двух частей.
- Первая часть рассказывает о приток денежных средств от инвестиций. Когда инвестор смотрит на инвестиции, ему представляют предполагаемую будущую стоимость инвестиций. Затем он может использовать метод приведенной стоимости. [i.e., PV = FV / (1 + i) ^n, where PV = Present Value, FV = Future Value, I = interest (cost of capital), and n = number of years] дисконтировать будущую стоимость и выяснить приток денежных средств от инвестиций на текущую дату.
- Во второй части рассказывается о стоимость инвестиций в проект. Это означает, сколько инвестор должен заплатить за инвестиции в настоящее время.
Если стоимость инвестиций меньше денежных поступлений от инвестиций, то проект вполне хорош для инвестора, так как он получает больше, чем платит. В противном случае, если стоимость инвестиций больше, чем денежные поступления от инвестиций, то лучше отказаться от проекта, так как инвестор должен заплатить больше, чем он платит на данный момент.
Примеры
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%}
Вы можете скачать этот шаблон Excel с чистой приведенной стоимостью здесь – Чистая приведенная стоимость Шаблон Excel
Hills Ltd. хотела бы инвестировать в новый проект. Компания располагает следующей информацией об этой новой инвестиции:
- Стоимость новых инвестиций на данный момент – 265 000 долларов США.
- Денежные поступления проект получит следующим образом:
- 1-й год — 60 000 долларов США
- 2-й год — 70 000 долларов США
- 3-й год — 80 000 долларов США
- 4-й год — 90 000 долларов
- 5-й год — 100 000 долларов США
Узнайте NPV и сделайте вывод, является ли это достойным вложением для Hills Ltd. Предположим, что норма прибыли равна 10%.
Используя приведенную выше информацию, мы можем легко выполнить расчет чистой приведенной стоимости новых инвестиций.
Приток денежных средств от инвестиций = 60 000 долл. США/1,1 + 70 000 долл. США/1,1 ^ 2 + 80 000 долл. США/1,1 ^ 3 + 90 000 долл. США/1,1 ^ 4 + 100 000 долл. США/1,1 ^ 5
= 54 545,5 + 57 851,2 + 60 105,2 + 61 471,2 + 62 092,1 = 296 065,2
Чистая приведенная стоимость = Приток денежных средств от инвестиций – Стоимость инвестиций
Или чистая приведенная стоимость = 296 065,2 долл. США – 265 000 долл. США = 31 065,2 долл. США.
Исходя из приведенного выше результата, мы можем быть уверены, что это достойная инвестиция; потому что чистая приведенная стоимость этих новых инвестиций положительна.
Использование NPV для оценки — пример использования Alibaba
В марте 2019 года Alibaba получит свободный денежный поток в размере 1,2 миллиарда долларов. Как мы отмечаем ниже, Alibaba будет генерировать предсказуемый положительный свободный денежный поток Денежные потоки Денежный поток в фирму или капитал после погашения всех долгов и обязательств называется свободным денежным потоком (FCF). Он измеряет, сколько денежных средств зарабатывает фирма после вычета необходимого оборотного капитала и капитальных затрат (CAPEX). подробнее.
- Шаг 1 заключается в применении формулы чистой приведенной стоимости для расчета приведенной стоимости явного периода FCFF.
- Шаг 2 заключается в применении формулы чистой приведенной стоимости для расчета PV конечной стоимости.
Общая сумма расчета NPV на шагах 1 и 2 дает нам общую стоимость предприятия Alibaba.
Ниже приведена таблица, обобщающая оценку DCF компании Alibaba. Оценка DCF. Анализ дисконтированных денежных потоков — это метод анализа текущей стоимости компании, инвестиций или денежных потоков путем корректировки будущих денежных потоков с учетом временной стоимости денег. Этот анализ оценивает текущую справедливую стоимость активов, проектов или компаний, принимая во внимание многие факторы, такие как инфляция, риск и стоимость капитала, а также анализируя будущие результаты деятельности компании.Подробнее.
Использование и актуальность
Используя эту формулу, инвесторы узнают разницу между денежными потоками от инвестиций и стоимостью инвестиций.
Он используется для принятия взвешенных деловых решений по следующим причинам:
- Во-первых, это очень легко вычислить. Прежде чем принимать какие-либо решения относительно инвестиций, если вы знаете, как рассчитать NPV, вы сможете принимать более обоснованные решения.
- Во-вторых, он сравнивает текущую стоимость притока и оттока денежных средств. В результате сравнение дает инвесторам правильную перспективу для принятия правильного решения.
- В-третьих, NPV предлагает вам окончательное решение. Рассчитав это, вы сразу узнаете, стоит ли идти на инвестиции или нет.
Калькулятор чистой приведенной стоимости
Вы можете использовать следующий калькулятор NPV
.cal-tbl td{ верхняя граница: 0 !важно; }.cal-tbl tr{ высота строки: 0.5em; } Только экран @media и (минимальная ширина устройства: 320 пикселей) и (максимальная ширина устройства: 480 пикселей) { .cal-tbl tr{ line-height: 1em !important; } }
Год1Год2Год3Год4Год5R (в процентах)Приток денежных средств от инвестицийСтоимость инвестицийФормула чистой приведенной стоимости =
Формула чистой приведенной стоимости =[Year1/(1 + R)1 + Year2/(1 + R)2 + Year3/(1 + R)3 + Year4/(1 + R)4 + Year5/(1 + R)5] − Стоимость инвестиций =
[0/(1+0)1 + 0/(1+0)2 + 0/(1+0)3 + 0/(1+0)4 + 0/(1+0)5] − 0=0
Чистая приведенная стоимость в Excel (с шаблоном Excel)
Давайте теперь сделаем тот же пример выше в Excel.
Это очень просто. Вам необходимо предоставить два входа: приток денежных средств от инвестиций и стоимость инвестиций.
Вы можете легко рассчитать NPV в ExcelNPV. В Excel NPV (чистая приведенная стоимость) инвестиций рассчитывается как разница между текущим притоком и оттоком денежных средств. Это функция Excel и финансовая формула, которая принимает значение скорости для притока и оттока в качестве входных данных. Подробнее предоставлен шаблон.
Шаг 1 – Найдите текущую стоимость притока денежных средств.
Шаг 2 – Найдите общую сумму текущих значений.
Шаг 3 – расчет чистой приведенной стоимости = 296 065,2 долл. США – 265 000 долл. США = 31 065,2 долл. США
Видео о чистой приведенной стоимости
Рекомендуемые статьи:
Это было руководство по чистой приведенной стоимости (NPV) и ее определению. Здесь мы обсудим формулу для расчета чистой приведенной стоимости, а также примеры, интерпретацию и использование. Вы также можете ознакомиться с приведенными ниже статьями, чтобы узнать больше о финансовом анализе.
- Формула значения в ExcelФормула значения В ExcelВ Excel функция значения возвращает значение текста, представляющего число. Итак, если у нас есть текст со значением $5, мы можем использовать формулу значения, чтобы получить в результате 5, поэтому эта функция дает нам числовое значение, представленное текстом.Подробнее
- Расчет дисконтированного периода окупаемости Расчет дисконтированного периода окупаемости Дисконтированный период окупаемости — это когда инвестиционный денежный поток окупает первоначальные инвестиции на основе временной стоимости денег. Он определяет ожидаемый доход от предлагаемой возможности капиталовложений. Он добавляет дисконтирование к первоначальному определению срока окупаемости, значительно повышая точность результата.Подробнее
- Функция NPV в Excel Функция NPV в ExcelЧистая приведенная стоимость (чистая приведенная стоимость) инвестиции рассчитывается как разница между текущим притоком и оттоком денежных средств. Это функция Excel и финансовая формула, которая принимает значение скорости для притока и оттока в качестве входных данных.Подробнее
- IRR против NPV























