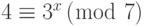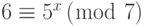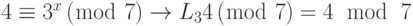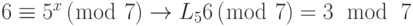From Wikipedia, the free encyclopedia
In modular arithmetic, a number g is a primitive root modulo n if every number a coprime to n is congruent to a power of g modulo n. That is, g is a primitive root modulo n if for every integer a coprime to n, there is some integer k for which gk ≡ a (mod n). Such a value k is called the index or discrete logarithm of a to the base g modulo n. So g is a primitive root modulo n if and only if g is a generator of the multiplicative group of integers modulo n.
Gauss defined primitive roots in Article 57 of the Disquisitiones Arithmeticae (1801), where he credited Euler with coining the term. In Article 56 he stated that Lambert and Euler knew of them, but he was the first to rigorously demonstrate that primitive roots exist for a prime n. In fact, the Disquisitiones contains two proofs: The one in Article 54 is a nonconstructive existence proof, while the proof in Article 55 is constructive.
Elementary example[edit]
The number 3 is a primitive root modulo 7[1] because
Here we see that the period of 3k modulo 7 is 6. The remainders in the period, which are 3, 2, 6, 4, 5, 1, form a rearrangement of all nonzero remainders modulo 7, implying that 3 is indeed a primitive root modulo 7. This derives from the fact that a sequence (gk modulo n) always repeats after some value of k, since modulo n produces a finite number of values. If g is a primitive root modulo n and n is prime, then the period of repetition is n − 1. Permutations created in this way (and their circular shifts) have been shown to be Costas arrays.
Definition[edit]
If n is a positive integer, the integers from 0 to n − 1 that are coprime to n (or equivalently, the congruence classes coprime to n) form a group, with multiplication modulo n as the operation; it is denoted by 
n, and is called the group of units modulo n, or the group of primitive classes modulo n. As explained in the article multiplicative group of integers modulo n, this multiplicative group (
n) is cyclic if and only if n is equal to 2, 4, pk, or 2pk where pk is a power of an odd prime number.[2][3][4] When (and only when) this group 
n is cyclic, a generator of this cyclic group is called a primitive root modulo n[5] (or in fuller language primitive root of unity modulo n, emphasizing its role as a fundamental solution of the roots of unity polynomial equations Xm
− 1 in the ring 

n.
When 
n is non-cyclic, such primitive elements mod n do not exist. Instead, each prime component of n has its own sub-primitive roots (see 15 in the examples below).
For any n (whether or not 
n is cyclic), the order of 
n is given by Euler’s totient function φ(n) (sequence A000010 in the OEIS). And then, Euler’s theorem says that aφ(n) ≡ 1 (mod n) for every a coprime to n; the lowest power of a that is congruent to 1 modulo n is called the multiplicative order of a modulo n. In particular, for a to be a primitive root modulo n, aφ(n) has to be the smallest power of a that is congruent to 1 modulo n.
Examples[edit]
For example, if n = 14 then the elements of 
n are the congruence classes {1, 3, 5, 9, 11, 13}; there are φ(14) = 6 of them. Here is a table of their powers modulo 14:
x x, x2, x3, ... (mod 14) 1 : 1 3 : 3, 9, 13, 11, 5, 1 5 : 5, 11, 13, 9, 3, 1 9 : 9, 11, 1 11 : 11, 9, 1 13 : 13, 1
The order of 1 is 1, the orders of 3 and 5 are 6, the orders of 9 and 11 are 3, and the order of 13 is 2. Thus, 3 and 5 are the primitive roots modulo 14.
For a second example let n = 15 . The elements of 
15 are the congruence classes {1, 2, 4, 7, 8, 11, 13, 14}; there are φ(15) = 8 of them.
x x, x2, x3, ... (mod 15) 1 : 1 2 : 2, 4, 8, 1 4 : 4, 1 7 : 7, 4, 13, 1 8 : 8, 4, 2, 1 11 : 11, 1 13 : 13, 4, 7, 1 14 : 14, 1
Since there is no number whose order is 8, there are no primitive roots modulo 15. Indeed, λ(15) = 4, where λ is the Carmichael function. (sequence A002322 in the OEIS)
Table of primitive roots[edit]
Numbers 
- = {1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 17, 18, 19, …} [6]
These are the numbers 

The following table lists the primitive roots modulo n up to 

|
primitive roots modulo 
|
order  (OEIS: A000010) |
exponent  (OEIS: A002322) |
|---|---|---|---|
| 1 | 0 | 1 | 1 |
| 2 | 1 | 1 | 1 |
| 3 | 2 | 2 | 2 |
| 4 | 3 | 2 | 2 |
| 5 | 2, 3 | 4 | 4 |
| 6 | 5 | 2 | 2 |
| 7 | 3, 5 | 6 | 6 |
| 8 | 4 | 2 | |
| 9 | 2, 5 | 6 | 6 |
| 10 | 3, 7 | 4 | 4 |
| 11 | 2, 6, 7, 8 | 10 | 10 |
| 12 | 4 | 2 | |
| 13 | 2, 6, 7, 11 | 12 | 12 |
| 14 | 3, 5 | 6 | 6 |
| 15 | 8 | 4 | |
| 16 | 8 | 4 | |
| 17 | 3, 5, 6, 7, 10, 11, 12, 14 | 16 | 16 |
| 18 | 5, 11 | 6 | 6 |
| 19 | 2, 3, 10, 13, 14, 15 | 18 | 18 |
| 20 | 8 | 4 | |
| 21 | 12 | 6 | |
| 22 | 7, 13, 17, 19 | 10 | 10 |
| 23 | 5, 7, 10, 11, 14, 15, 17, 19, 20, 21 | 22 | 22 |
| 24 | 8 | 2 | |
| 25 | 2, 3, 8, 12, 13, 17, 22, 23 | 20 | 20 |
| 26 | 7, 11, 15, 19 | 12 | 12 |
| 27 | 2, 5, 11, 14, 20, 23 | 18 | 18 |
| 28 | 12 | 6 | |
| 29 | 2, 3, 8, 10, 11, 14, 15, 18, 19, 21, 26, 27 | 28 | 28 |
| 30 | 8 | 4 | |
| 31 | 3, 11, 12, 13, 17, 21, 22, 24 | 30 | 30 |
Properties[edit]
Gauss proved[7] that for any prime number p (with the sole exception of p = 3), the product of its primitive roots is congruent to 1 modulo p.
He also proved[8] that for any prime number p, the sum of its primitive roots is congruent to μ(p − 1) modulo p, where μ is the Möbius function.
For example,
-
p = 3, μ(2) = −1. The primitive root is 2. p = 5, μ(4) = 0. The primitive roots are 2 and 3. p = 7, μ(6) = 1. The primitive roots are 3 and 5. p = 31, μ(30) = −1. The primitive roots are 3, 11, 12, 13, 17, 21, 22 and 24.
E.g., the product of the latter primitive roots is 

If 


Artin’s conjecture on primitive roots states that a given integer a that is neither a perfect square nor −1 is a primitive root modulo infinitely many primes.
Finding primitive roots[edit]
No simple general formula to compute primitive roots modulo n is known.[a][b] There are however methods to locate a primitive root that are faster than simply trying out all candidates. If the multiplicative order (its exponent) of a number m modulo n is equal to 

n), then it is a primitive root. In fact the converse is true: If m is a primitive root modulo n, then the multiplicative order of m is 
For 


using a fast algorithm for modular exponentiation such as exponentiation by squaring. A number g for which these k results are all different from 1 is a primitive root.
The number of primitive roots modulo n, if there are any, is equal to[9]
since, in general, a cyclic group with r elements has 
For prime n, this equals 

If g is a primitive root modulo p, then g is also a primitive root modulo all powers pk unless gp−1 ≡ 1 (mod p2); in that case, g + p is.[11]
If g is a primitive root modulo pk, then g is also a primitive root modulo all smaller powers of p.
If g is a primitive root modulo pk, then either g or g + pk (whichever one is odd) is a primitive root modulo 2pk.[11]
Finding primitive roots modulo p is also equivalent to finding the roots of the (p − 1)st cyclotomic polynomial modulo p.
Order of magnitude of primitive roots[edit]
The least primitive root gp modulo p (in the range 1, 2, …, p − 1 ) is generally small.
Upper bounds[edit]
Burgess (1962) proved[12][13] that for every ε > 0 there is a C such that 
Grosswald (1981) proved[12][14] that if 

Shoup (1990, 1992) proved,[15] assuming the generalized Riemann hypothesis, that gp = O(log6 p).
Lower bounds[edit]
Fridlander (1949) and Salié (1950) proved[12] that there is a positive constant C such that for infinitely many primes gp > C log p .
It can be proved[12] in an elementary manner that for any positive integer M there are infinitely many primes such that M < gp < p − M .
Applications[edit]
A primitive root modulo n is often used in pseudorandom number generators[16] and cryptography, including the Diffie–Hellman key exchange scheme. Sound diffusers have been based on number-theoretic concepts such as primitive roots and quadratic residues.[17][18]
See also[edit]
- Dirichlet character
- Full reptend prime
- Gauss’s generalization of Wilson’s theorem
- Multiplicative order
- Quadratic residue
- Root of unity modulo n
Footnotes[edit]
- ^ «One of the most important unsolved problems in the theory of finite fields is designing a fast algorithm to construct primitive roots. von zur Gathen & Shparlinski 1998, pp. 15–24
- ^ «There is no convenient formula for computing [the least primitive root].» Robbins 2006, p. 159
References[edit]
- ^ Stromquist, Walter. «What are primitive roots?». Mathematics. Bryn Mawr College. Archived from the original on 2017-07-03. Retrieved 2017-07-03.
- ^ Weisstein, Eric W. «Modulo Multiplication Group». MathWorld.
- ^ Primitive root, Encyclopedia of Mathematics.
- ^ Vinogradov 2003, pp. 105–121, § VI Primitive roots and indices.
- ^ Vinogradov 2003, p. 106.
- ^ Gauss & Clarke 1986, art 92.
- ^ Gauss & Clarke 1986, arts. 80.
- ^ Gauss & Clarke 1986, art 81.
- ^ (sequence A010554 in the OEIS)
- ^ Knuth, Donald E. (1998). Seminumerical Algorithms. The Art of Computer Programming. Vol. 2 (3rd ed.). Addison–Wesley. section 4.5.4, page 391.
- ^ a b Cohen, Henri (1993). A Course in Computational Algebraic Number Theory. Berlin: Springer. p. 26. ISBN 978-3-540-55640-4.
- ^ a b c d Ribenboim, Paulo (1996). The New Book of Prime Number Records. New York, NY: Springer. p. 24. ISBN 978-0-387-94457-9.
- ^ Burgess, D. A. (1962). «On Character Sums and Primitive Roots †». Proceedings of the London Mathematical Society. s3-12 (1): 179–192. doi:10.1112/plms/s3-12.1.179.
- ^ Grosswald, E. (1981). «On Burgess’ Bound for Primitive Roots Modulo Primes and an Application to Γ(p)». American Journal of Mathematics. 103 (6): 1171–1183. doi:10.2307/2374229. ISSN 0002-9327. JSTOR 2374229.
- ^ Bach & Shallit 1996, p. 254.
- ^ Gentle, James E. (2003). Random number generation and Monte Carlo methods (2nd ed.). New York: Springer. ISBN 0-387-00178-6. OCLC 51534945.
- ^ Walker, R. (1990). The design and application of modular acoustic diffusing elements (PDF). BBC Research Department (Report). British Broadcasting Corporation. Retrieved 25 March 2019.
- ^ Feldman, Eliot (July 1995). «A reflection grating that nullifies the specular reflection: A cone of silence». J. Acoust. Soc. Am. 98 (1): 623–634. Bibcode:1995ASAJ…98..623F. doi:10.1121/1.413656.
Sources[edit]
- Bach, Eric; Shallit, Jeffrey (1996). Efficient Algorithms. Algorithmic Number Theory. Vol. I. Cambridge, MA: The MIT Press. ISBN 978-0-262-02405-1.
- Carella, N. A. (2015). «Least Prime Primitive Roots». International Journal of Mathematics and Computer Science. 10 (2): 185–194. arXiv:1709.01172.
The Disquisitiones Arithmeticae has been translated from Gauss’s Ciceronian Latin into English and German. The German edition includes all of his papers on number theory: all the proofs of quadratic reciprocity, the determination of the sign of the Gauss sum, the investigations into biquadratic reciprocity, and unpublished notes.
- Gauss, Carl Friedrich (1986) [1801]. Disquisitiones Arithmeticae. Translated by Clarke, Arthur A. (2nd, corrected ed.). New York, NY: Springer. ISBN 978-0-387-96254-2.
- Gauss, Carl Friedrich (1965) [1801]. Untersuchungen über höhere Arithmetik [Studies of Higher Arithmetic] (in German). Translated by Maser, H. (2nd ed.). New York, NY: Chelsea. ISBN 978-0-8284-0191-3.
- Robbins, Neville (2006). Beginning Number Theory. Jones & Bartlett Learning. ISBN 978-0-7637-3768-9.
- Vinogradov, I.M. (2003). «§ VI Primitive roots and indices». Elements of Number Theory. Mineola, NY: Dover Publications. pp. 105–121. ISBN 978-0-486-49530-9.
- von zur Gathen, Joachim; Shparlinski, Igor (1998). «Orders of Gauss periods in finite fields». Applicable Algebra in Engineering, Communication and Computing. 9 (1): 15–24. CiteSeerX 10.1.1.46.5504. doi:10.1007/s002000050093. MR 1624824. S2CID 19232025.
Further reading[edit]
- Ore, Oystein (1988). Number Theory and Its History. Dover. pp. 284–302. ISBN 978-0-486-65620-5..
External links[edit]
- Weisstein, Eric W. «Primitive Root». MathWorld.
- Holt. «Quadratic residues and primitive roots». Mathematics. Michigan Tech.
- «Primitive roots calculator». BlueTulip.
Поскольку примитивные корни в теории чисел являются одним из разделов математики , определенные элементы группы классов редуцированных вычетов обозначаются. Определяющим свойством примитивного корня является то, что каждый элемент группы классов простых вычетов может быть представлен как одна из его степеней .
пример
Число 3 является примитивным корнем по модулю 7, поскольку применяется следующее
Все элементы группы классов простых остатков могут быть представлены по модулю 7 как степени 3, причем показатель степени является индексом, присвоенным соответствующему элементу ( дискретный логарифм ). Число 2 не является примитивным корнем по модулю 7, поэтому остатки повторяются в последовательности степеней 2 по модулю 7
после 3 шагов каждый, поэтому не все 6 различных простых вычетов по модулю 7 достигаются, и 2 не порождает группу классов простых вычетов .
Определение и условия существования
Целое число является примитивным корнем по модулю, если класс вычетов создает группу классов простых вычетов . Это означает, что целое число является примитивным корнем по модулю тогда и только тогда, когда порядок по модулю равен порядку группы группы классов простых вычетов:



-
.
Здесь, в φ функция Эйлера и мультипликативный порядок по модулю т члена , д. ЧАС. наименьший положительный показатель, для которого равен (обозначение «mod» см. по модулю ).
Кстати , именно тогда тоже
-
,
где функция Кармайкл .
Есть примитивные корни по модулю тогда и только тогда , когда простой класс вычетов группа является циклической группой . Согласно теореме К.Ф. Гаусса , это так тогда и только тогда, когда для модуля
применяется. Он обозначает набор простых чисел.
Если есть примитивные корни по модулю , то есть в точности по модулю инконгруэнтные примитивные корни . Каждый из этих примитивных корней конгруэнтен по модулю элементу множества:
где любой первообразный корень — по модулю .
Расчет первобытных корней
Попытка (грубая сила)
Чтобы определить, является ли число примитивным корнем по модулю , сначала вычисляется , а затем порядок . Порядок можно определить, например, путем последовательного вычисления значений для . Первое, что нужно сделать, это порядок .
В примере из введения вы можете видеть, что 3 имеет порядок 6. Так как, кроме того , 3 является первообразным корнем по модулю 7.
Число, которое не является примитивным корнем по модулю 7, равно 4. Здесь применяется
Следовательно, порядок 4 равен 3, а 4 не является первообразным корнем по модулю 7.
Можно сэкономить массу экспериментов, используя тот факт, что порядок делится согласно теореме Лагранжа , поскольку каждое число, для которого выполняется, делится на порядок. Следовательно, нужно только проверить все факторы , отображающие ли возведение в степень с их помощью число в 1, и наименьший такой делитель — это порядок.
Примитивные корни по модулю простых чисел
Группы классов простых вычетов для модулей , являющихся простыми числами, состоят ровно из элементов. Цифры представляют разные классы остатка. Если примитивный корень по модулю , то выражение принимает для всех значений из (в случайном порядке , по- видимому).
Примеры
В следующей таблице показаны первообразные корни по модулю простых чисел до 29.
 |
 |
Первобытные корни по модулю 
|
|---|---|---|
| 2 | 1 | 1 |
| 3 | 1 | 2 |
| 5 | 2 | 2, 3 |
| 7-е | 2 | 3, 5 |
| 11 | 4-й | 2, 6, 7, 8 |
| 13-е | 4-й | 2, 6, 7, 11 |
| 17-е | 8-е | 3, 5, 6, 7, 10, 11, 12, 14 |
| 19-е | 6-е | 2, 3, 10, 13, 14, 15 |
| 23 | 10 | 5, 7, 10, 11, 14, 15, 17, 19, 20, 21 |
| 29 | 12-е | 2, 3, 8, 10, 11, 14, 15, 18, 19, 21, 26, 27 |
Первобытные корни по модулю простых степеней
Если с нечетным простым числом, то примитивный корень по модулю с также первообразного корнем по модулю меньших степеней . Что интересно для поиска первообразных корней по модулю более высоких степеней, так это то, что примитивный корень является по модулю (с ) также примитивным корнем для всех высших степеней . Таким образом, для более высоких степеней простого числа ,
достаточно
Затем с каждым номером , определенным во втором шаге один имеет примитивный корень по модуль для любого числа .
Если полученный таким образом первообразный корень нечетный, то он также является примитивным корнем по модулю , в противном случае это применимо к .
Пример применения
Примитивные корни используются в обмене ключами Диффи-Хеллмана , криптографическом методе обмена открытыми ключами, опубликованном в 1976 году . Его безопасность основана на том, что
это но
веб ссылки
- Вычисление первообразных корней
литература
« Арифметические исследования» были опубликованы на латыни Карлом Фридрихом Гаусом . Современный немецкий перевод включает все его работы по теории чисел:
- Карл Фридрих Гаус : Исследования по высшей арифметике (немецкий перевод), оригинал: Лейпциг 1801.
- Питер Бундшу : Введение в теорию чисел . 5-е издание. Springer Verlag, 2002, ISBN 3-540-43579-4 , стр. 109-120
- Армин Лойбехер: Теория чисел — Введение в алгебру . 1-е издание. Springer Verlag, 1996, Берлин, Гейдельберг, Нью-Йорк. ISBN 3-540-58791-8 .
Индивидуальные доказательства
-
↑ Последнее, как правило, ближе к порядку элементов, потому что оно применимо ко всем
-
.
-
- ↑ a b c А. Лейтбехер: Теория чисел — Введение в алгебру. С. 53-54.
- ↑ Карл Фридрих Гаусс: Исследования по высшей арифметике. Г. Мазер, 1889, р. Ст. 92 , доступ к 30 января 2017 .
В модульной арифметике, ветви теории чисел, число g является примитивным корнем по модулю n, если каждое число a , взаимно простое с n конгруэнтно степени g по модулю n. То есть g является примитивным корнем по модулю n, если для каждого целого числа, взаимно простого с n, существует целое число k такое, что g ≡ a (mod n). Такое значение k называется индексом или дискретным логарифмом числа a по основанию g по модулю n. Обратите внимание, что g является примитивным корнем по модулю n тогда и только тогда, когда g является генератором мультипликативной группы целых чисел по модулю n.
Гаусс, определенный в статье 57 Disquisitiones Arithmeticae (1801 г.), где он приписал Эйлеру создание этого термина. В статье 56 он заявил, что Ламберт и Эйлер знали о них, но он был первым, кто строго продемонстрировал, что примитивные корни существуют для простого n. Фактически, Disquisitiones содержит два доказательства: одно в статье 54 является неконструктивным доказательством существования, а другое в статье 55 является конструктивным.
Содержание
- 1 Элементарный пример
- 2 Определение
- 3 Примеры
- 3.1 Таблица первообразных корней
- 3.2 Арифметические факты
- 4 Поиск первообразных корней
- 5 Порядок величины первообразных корней
- 5.1 Верхние границы
- 5.2 Нижние границы
- 6 Приложения
- 7 См. Также
- 8 Примечания
- 9 Ссылки
- 10 Дополнительная литература
- 11 Внешние ссылки
Элементарный пример
Число 3 является примитивом корень по модулю 7, поскольку
-
- 3 1 = 3 = 3 0 × 3 ≡ 1 × 3 = 3 ≡ 3 (mod 7) 3 2 = 9 = 3 1 × 3 ≡ 3 × 3 = 9 ≡ 2 (mod 7) 3 3 = 27 = 3 2 × 3 ≡ 2 × 3 = 6 ≡ 6 (mod 7) 3 4 = 81 = 3 3 × 3 ≡ 6 × 3 = 18 ≡ 4 (mod 7) 3 5 = 243 = 3 4 × 3 ≡ 4 × 3 = 12 ≡ 5 (модуль 7) 3 6 = 729 = 3 5 × 3 ≡ 5 × 3 = 15 ≡ 1 (модуль 7) 3 7 = 2187 = 3 6 × 3 ≡ 1 × 3 = 3 ≡ 3 (мод 7) { displaystyle { begin {array} {rcrcrcrcrcr} 3 ^ {1} = 3 = 3 ^ {0} times 3 eq uiv 1 times 3 = 3 Equiv 3 { pmod {7}} \ 3 ^ {2} = 9 = 3 ^ {1} times 3 Equiv 3 times 3 = 9 Equiv 2 { pmod {7}} \ 3 ^ {3} = 27 = 3 ^ {2} times 3 Equiv 2 times 3 = 6 Equiv 6 { pmod {7}} \ 3 ^ {4} = 81 = 3 ^ {3} times 3 Equiv 6 times 3 = 18 Equiv 4 { pmod {7}} \ 3 ^ {5} = 243 = 3 ^ {4} times 3 Equiv 4 times 3 = 12 Equiv 5 { pmod {7}} \ 3 ^ {6} = 729 = 3 ^ {5} times 3 Equiv 5 times 3 = 15 Equiv 1 { pmod {7 }} \ 3 ^ {7} = 2187 = 3 ^ {6} times 3 Equiv 1 times 3 = 3 Equiv 3 { pmod {7}} \ end {array}}}
- 3 1 = 3 = 3 0 × 3 ≡ 1 × 3 = 3 ≡ 3 (mod 7) 3 2 = 9 = 3 1 × 3 ≡ 3 × 3 = 9 ≡ 2 (mod 7) 3 3 = 27 = 3 2 × 3 ≡ 2 × 3 = 6 ≡ 6 (mod 7) 3 4 = 81 = 3 3 × 3 ≡ 6 × 3 = 18 ≡ 4 (mod 7) 3 5 = 243 = 3 4 × 3 ≡ 4 × 3 = 12 ≡ 5 (модуль 7) 3 6 = 729 = 3 5 × 3 ≡ 5 × 3 = 15 ≡ 1 (модуль 7) 3 7 = 2187 = 3 6 × 3 ≡ 1 × 3 = 3 ≡ 3 (мод 7) { displaystyle { begin {array} {rcrcrcrcrcr} 3 ^ {1} = 3 = 3 ^ {0} times 3 eq uiv 1 times 3 = 3 Equiv 3 { pmod {7}} \ 3 ^ {2} = 9 = 3 ^ {1} times 3 Equiv 3 times 3 = 9 Equiv 2 { pmod {7}} \ 3 ^ {3} = 27 = 3 ^ {2} times 3 Equiv 2 times 3 = 6 Equiv 6 { pmod {7}} \ 3 ^ {4} = 81 = 3 ^ {3} times 3 Equiv 6 times 3 = 18 Equiv 4 { pmod {7}} \ 3 ^ {5} = 243 = 3 ^ {4} times 3 Equiv 4 times 3 = 12 Equiv 5 { pmod {7}} \ 3 ^ {6} = 729 = 3 ^ {5} times 3 Equiv 5 times 3 = 15 Equiv 1 { pmod {7 }} \ 3 ^ {7} = 2187 = 3 ^ {6} times 3 Equiv 1 times 3 = 3 Equiv 3 { pmod {7}} \ end {array}}}
Здесь мы видим, что период числа 3 по модулю 7 равен 6. Остатки в периоде, равные 3, 2, 6, 4, 5, 1, образуют перестановку всех ненулевых остатков по модулю 7, подразумевая, что 3 действительно является примитивным корнем по модулю 7. Это происходит из того факта, что последовательность (g по модулю n) всегда повторяется после некоторого значения k, поскольку по модулю n получается конечное число значений. Если g — примитивный корень по модулю n, а n — простое число, то период повторения равен n − 1. Любопытно, что созданные таким образом перестановки (и их круговые сдвиги) оказались массивами Костаса.
Определение
Если n — положительное целое число, целые числа от 0 до n — 1, которые взаимно простые с n (или эквивалентно, классы конгруэнтности взаимно простые с n) образуют группу с умножением по модулю n в качестве операции; она обозначается Z. n и называется группой единиц по модулю n или группой примитивных классов по модулю n. Как объясняется в статье мультипликативная группа целых чисел по модулю n, эта мультипликативная группа (Z. n) является циклической тогда и только тогда, когда n равно 2, 4, p или 2p, где p — степень нечетного простого числа. Когда (и только когда) эта группа Z. nявляется циклической, генератор этой циклической группы называется примитивным корнем по модулю n (или на более полном языке примитивным корнем единицы по модулю n, подчеркивая ее роль как фундаментального решения корней из единицы полиномиальных уравнений X. — 1 в кольце Z. n), или просто примитивный элемент Z. n. Когда Z. nнециклический, таких примитивных элементов по модулю n не существует.
Для любого n (независимо от того, является ли Z. nциклическим или нет), порядок (т. Е. Количество элементов в) Z. nзадается функцией Эйлера φ ( n) (последовательность A000010 в OEIS ). И затем, теорема Эйлера говорит, что a 1 (mod n) для каждого взаимно простого с n; наименьшая степень числа a, которая сравнима с 1 по модулю n, называется мультипликативным порядком по модулю n. В частности, чтобы a было первообразным корнем по модулю n, φ (n) должна быть наименьшей степенью a, которая сравнима с 1 по модулю n.
Примеры
Например, если n = 14, то элементы Z. nявляются классами конгруэнтности {1, 3, 5, 9, 11, 13}; их φ (14) = 6. Вот таблица их мощностей по модулю 14:
xx, x, x,... (mod 14) 1: 1 3: 3, 9, 13, 11, 5, 1 5: 5, 11, 13, 9, 3, 1 9: 9, 11, 1 11: 11, 9, 1 13: 13, 1
Порядок 1 равен 1, порядок 3 и 5 равен 6, порядки 9 и 11 равны 3, а порядок 13 равен 2. Таким образом, 3 и 5 являются первообразными корнями по модулю 14.
Для второго примера пусть n = 15. Элементы Z. 15равны классы конгруэнции {1, 2, 4, 7, 8, 11, 13, 14}; их φ (15) = 8.
xx, x, x,... (mod 15) 1: 1 2: 2, 4, 8, 1 4: 4, 1 7: 7, 4, 13, 1 8: 8, 4, 2, 1 11: 11, 1 13: 13, 4, 7, 1 14: 14, 1
Поскольку нет числа, порядок которого равен 8, нет примитивных корней по модулю 15. В самом деле, λ (15) = 4, где λ — функция Кармайкла. (последовательность A002322 в OEIS )
Таблице примитивных корней
Числа, которые имеют примитивный корень:
- 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 17, 18, 19, 22, 23, 25, 26, 27, 29, 31, 34, 37, 38, 41, 43, 46, 47, 49, 50, 53, 54, 58, 59, 61, 62, 67, 71, 73, 74, 79, 81, 82, 83, 86, 89, 94, 97, 98, 101, 103, 106, 107, 109, 113, 118, 121, 122, 125, 127, 131, 134, 137, 139, 142, 146, 149,… (последовательность A033948 в OEIS )
Это таблица Гаусса примитивные корни из Disquisitiones. В отличие от большинства современных авторов, он не всегда выбирал наименьший примитивный корень. Вместо этого он выбрал 10, если это примитивный корень; если это не так, он выбрал тот корень, который дает 10 наименьший индекс, и, если их несколько, выберите наименьший из них. Это не только для облегчения ручных вычислений, но и используется в § VI, где исследуются периодические десятичные разложения рациональных чисел.
Строки таблицы помечены простые степени (кроме 2, 4 и 
Например, в строке 11, 2 задается как первообразный корень, а в столбце 5 запись равна 4. Это означает, что 2 = 16 ≡ 5 (mod 11).
Для индекса составного числа сложите индексы его простых множителей.
Например, в строке 11 индекс 6 представляет собой сумму индексов для 2 и 3: 2 = 512 ≡ 6 ( мод 11). Индекс 25 вдвое больше индекса 5: 2 = 256 ≡ 25 (мод 11). (Конечно, поскольку 25 ≡ 3 (mod 11), запись для 3 равна 8).
Таблица проста для нечетных простых степеней. Но степени числа 2 (16, 32 и 64) не имеют примитивных корней; вместо этого, степени 5 составляют половину нечетных чисел, меньших степени 2, а их отрицательные значения по модулю степени 2 составляют вторую половину. Все степени 5 равны 5 или 1 (mod 8); столбцы, озаглавленные числами 3 или 7 (mod 8), содержат индекс его отрицательного значения. (Последовательность A185189 и A185268 в OEIS )
Например, по модулю 32 индекс для 7 равен 2, а 5 = 25 ≡ −7 (mod 32), но запись для 17 — 4, и 5 = 625 ≡ 17 (mod 32).
| n | root | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 | 97 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 2 | 1 | ||||||||||||||||||||||||||||
| 5 | 2 | 1 | 3 | |||||||||||||||||||||||||||
| 7 | 3 | 2 | 1 | 5 | ||||||||||||||||||||||||||
| 9 | 2 | 1 | * | 5 | 4 | |||||||||||||||||||||||||
| 11 | 2 | 1 | 8 | 4 | 7 | |||||||||||||||||||||||||
| 13 | 6 | 5 | 8 | 9 | 7 | 11 | ||||||||||||||||||||||||
| 16 | 5 | * | 3 | 1 | 2 | 1 | 3 | |||||||||||||||||||||||
| 17 | 10 | 10 | 11 | 7 | 9 | 13 | 12 | |||||||||||||||||||||||
| 19 | 10 | 17 | 5 | 2 | 12 | 6 | 13 | 8 | ||||||||||||||||||||||
| 23 | 10 | 8 | 20 | 15 | 21 | 3 | 12 | 17 | 5 | |||||||||||||||||||||
| 25 | 2 | 1 | 7 | * | 5 | 16 | 19 | 13 | 18 | 11 | ||||||||||||||||||||
| 27 | 2 | 1 | * | 5 | 16 | 13 | 8 | 15 | 12 | 11 | ||||||||||||||||||||
| 29 | 10 | 11 | 27 | 18 | 20 | 23 | 2 | 7 | 15 | 24 | ||||||||||||||||||||
| 31 | 17 | 12 | 13 | 20 | 4 | 29 | 23 | 1 | 22 | 21 | 27 | |||||||||||||||||||
| 32 | 5 | * | 3 | 1 | 2 | 5 | 7 | 4 | 7 | 6 | 3 | 0 | ||||||||||||||||||
| 37 | 5 | 11 | 34 | 1 | 28 | 6 | 13 | 5 | 25 | 21 | 15 | 27 | ||||||||||||||||||
| 41 | 6 | 26 | 15 | 22 | 39 | 3 | 31 | 33 | 9 | 36 | 7 | 28 | 32 | |||||||||||||||||
| 43 | 28 | 39 | 17 | 5 | 7 | 6 | 40 | 16 | 29 | 20 | 25 | 32 | 35 | 18 | ||||||||||||||||
| 47 | 10 | 30 | 18 | 17 | 38 | 27 | 3 | 42 | 29 | 39 | 43 | 5 | 24 | 25 | 37 | |||||||||||||||
| 49 | 10 | 2 | 13 | 41 | * | 16 | 9 | 31 | 35 | 32 | 24 | 7 | 38 | 27 | 36 | 23 | ||||||||||||||
| 53 | 26 | 25 | 9 | 31 | 38 | 46 | 28 | 42 | 41 | 39 | 6 | 45 | 22 | 33 | 30 | 8 | ||||||||||||||
| 59 | 10 | 25 | 32 | 34 | 44 | 45 | 28 | 14 | 22 | 27 | 4 | 7 | 41 | 2 | 13 | 53 | 28 | |||||||||||||
| 61 | 10 | 47 | 42 | 14 | 23 | 45 | 20 | 49 | 22 | 39 | 25 | 13 | 33 | 18 | 41 | 40 | 51 | 17 | ||||||||||||
| 64 | 5 | * | 3 | 1 | 10 | 5 | 15 | 12 | 7 | 14 | 11 | 8 | 9 | 14 | 13 | 12 | 5 | 1 | 3 | |||||||||||
| 67 | 12 | 29 | 9 | 39 | 7 | 61 | 23 | 8 | 26 | 20 | 22 | 43 | 44 | 19 | 63 | 64 | 3 | 54 | 5 | |||||||||||
| 71 | 62 | 58 | 18 | 14 | 33 | 43 | 27 | 7 | 38 | 5 | 4 | 13 | 30 | 55 | 44 | 17 | 59 | 29 | 37 | 11 | ||||||||||
| 73 | 5 | 8 | 6 | 1 | 33 | 55 | 59 | 21 | 62 | 46 | 35 | 11 | 64 | 4 | 51 | 31 | 53 | 5 | 58 | 50 | 44 | |||||||||
| 79 | 29 | 50 | 71 | 34 | 19 | 70 | 74 | 9 | 10 | 52 | 1 | 76 | 23 | 21 | 47 | 55 | 7 | 17 | 75 | 54 | 33 | 4 | ||||||||
| 81 | 11 | 25 | * | 35 | 22 | 1 | 38 | 15 | 12 | 5 | 7 | 14 | 24 | 29 | 10 | 13 | 45 | 53 | 4 | 20 | 33 | 48 | 52 | |||||||
| 83 | 50 | 3 | 52 | 81 | 24 | 72 | 67 | 4 | 59 | 16 | 36 | 32 | 60 | 38 | 49 | 69 | 13 | 20 | 34 | 53 | 17 | 43 | 47 | |||||||
| 89 | 30 | 72 | 87 | 18 | 7 | 4 | 65 | 82 | 53 | 31 | 29 | 57 | 77 | 67 | 59 | 34 | 10 | 45 | 19 | 32 | 26 | 68 | 46 | 27 | ||||||
| 97 | 10 | 86 | 2 | 11 | 53 | 82 | 83 | 19 | 27 | 79 | 47 | 26 | 41 | 71 | 44 | 60 | 14 | 65 | 32 | 51 | 25 | 20 | 42 | 91 | 18 | |||||
| n | корень | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 | 97 |
В следующей таблице перечислены первообразные корни по модулю n для n ≤ 72:
n { displaystyle n} |
примитивные корни по модулю n { displaystyle n} |
порядок (OEIS : A000010 ) | n { displaystyle n} |
примитивные корни по модулю n { displaystyle n} |
order (OEIS : A000010 ) |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 37 | 2, 5, 13, 15, 17, 18, 19, 20, 22, 24, 32, 35 | 36 |
| 2 | 1 | 1 | 38 | 3, 13, 15, 21, 29, 33 | 18 |
| 3 | 2 | 2 | 39 | 24 | |
| 4 | 3 | 2 | 40 | 16 | |
| 5 | 2, 3 | 4 | 41 | 6, 7, 11, 12, 13, 15, 17, 19, 22, 24, 26, 28, 29, 30, 34, 35 | 40 |
| 6 | 5 | 2 | 42 | 12 | |
| 7 | 3, 5 | 6 | 43 | 3, 5, 12, 18, 19, 20, 26, 28, 29, 30, 33, 34 | 42 |
| 8 | 4 | 44 | 20 | ||
| 9 | 2, 5 | 6 | 45 | 24 | |
| 10 | 3, 7 | 4 | 46 | 5, 7, 11, 15, 17, 19, 21, 33, 37, 43 | 22 |
| 11 | 2, 6, 7, 8 | 10 | 47 | 5, 10, 11, 13, 15, 19, 20, 22, 23, 26, 29, 30, 31, 33, 35, 38, 39, 40, 41, 43, 44, 45 | 46 |
| 12 | 4 | 48 | 16 | ||
| 13 | 2, 6, 7, 11 | 12 | 49 | 3, 5, 10, 12, 17, 24, 26, 33, 38, 40, 45, 47 | 42 |
| 14 | 3, 5 | 6 | 50 | 3, 13, 17, 23, 27, 33, 37, 47 | 20 |
| 15 | 8 | 51 | 32 | ||
| 16 | 8 | 52 | 24 | ||
| 17 | 3, 5, 6, 7, 10, 11, 12, 14 | 16 | 53 | 2, 3, 5, 8, 12, 14, 18, 19, 20, 21, 22, 26, 27, 31, 32, 33, 34, 35, 39, 41, 45, 48, 50, 51 | 52 |
| 18 | 5, 11 | 6 | 54 | 5, 11, 23, 29, 41, 47 | 18 |
| 19 | 2, 3, 10, 13, 14, 15 | 18 | 55 | 40 | |
| 20 | 8 | 56 | 24 | ||
| 21 | 12 | 57 | 36 | ||
| 22 | 7, 13, 17, 19 | 10 | 58 | 3, 11, 15, 19, 21, 27, 31, 37, 39, 43, 47, 55 | 28 |
| 23 | 5, 7, 10, 11, 14, 15, 17, 19, 20, 21 | 22 | 59 | 2, 6, 8, 10, 11, 13, 14, 18, 23, 24, 30, 31, 32, 33, 34, 37, 38, 39, 40, 42, 43, 44, 47, 50, 52, 54, 55, 56 | 58 |
| 24 | 8 | 60 | 16 | ||
| 25 | 2, 3, 8, 12, 13, 17, 22, 23 | 20 | 61 | 2, 6, 7, 10, 17, 18, 26, 30, 31, 35, 43, 44, 51, 54, 55, 59 | 60 |
| 26 | 7, 11, 15, 19 | 12 | 62 | 3, 11, 13, 17, 21, 43, 53, 55 | 30 |
| 27 | 2, 5, 11, 14, 20, 23 | 18 | 63 | 36 | |
| 28 | 12 | 64 | 32 | ||
| 29 | 2, 3, 8, 10, 11, 14, 15, 18, 19, 21, 26, 27 | 28 | 65 | 48 | |
| 30 | 8 | 66 | 20 | ||
| 31 | 3, 11, 12, 13, 17, 21, 22, 24 | 30 | 67 | 2, 7, 11, 12, 13, 18, 20, 28, 31, 32, 34, 41, 44, 46, 48, 50, 51, 57, 61, 63 | 66 |
| 32 | 16 | 68 | 32 | ||
| 33 | 20 | 69 | 44 | ||
| 34 | 3, 5, 7, 11, 23, 27, 29, 31 | 16 | 70 | 24 | |
| 35 | 24 | 71 | 7, 11, 13, 21, 22, 28, 31, 33, 35, 42, 44, 47, 52, 53, 55, 56, 59, 61, 62, 63, 65, 67, 68, 69 | 70 | |
| 36 | 12 | 72 | 24 |
Гипотеза Артина о первообразном корне s утверждает, что данное целое число a, которое не является ни полным квадратом, ни −1, является первообразным корнем по модулю бесконечного числа простых чисел.
Последовательность наименьших примитивных корней по модулю n ( не то же самое, что последовательность примитивных корней в таблице Гаусса)
- 0, 1, 2, 3, 2, 5, 3, 0, 2, 3, 2, 0, 2, 3, 0, 0, 3, 5, 2, 0, 0, 7, 5, 0, 2, 7, 2, 0, 2, 0, 3, 0, 0, 3, 0, 0, 2, 3, 0, 0, 6, 0, 3, 0, 0, 5, 5, 0, 3, 3, 0, 0, 2, 5, 0, 0, 0, 3, 2, 0, 2, 3, 0, 0, 0, 0, 2, 0, 0, 0, 7, 0, 5, 5, 0,… (последовательность A046145 в OEIS )
Для простого n они равны
- 1, 2, 2, 3, 2, 2, 3, 2, 5, 2, 3, 2, 6, 3, 5, 2, 2, 2, 2, 7, 5, 3, 2, 3, 5, 2, 5, 2, 6, 3, 3, 2, 3, 2, 2, 6, 5, 2, 5, 2, 2, 2, 19, 5, 2, 3, 2, 3, 2, 6, 3, 7, 7, 6, 3, 5, 2, 6, 5, 3, 3, 2, 5, 17, 10, 2, 3, 10, 2, 2, 3, 7, 6, 2, 2,… (последовательность A001918 в OEIS )
Наибольшие примитивные корни по модулю n равны
- 0, 1, 2, 3, 3, 5, 5, 0, 5, 7, 8, 0, 11, 5, 0, 0, 14, 11, 15, 0, 0, 19, 21, 0, 23, 19, 23, 0, 27, 0, 24, 0, 0, 31, 0, 0, 35, 33, 0, 0, 35, 0, 34, 0, 0, 43, 45, 0, 47, 47, 0, 0, 51, 47, 0, 0, 0, 55, 56, 0, 59, 55, 0, 0, 0, 0, 63, 0, 0, 0, 69, 0, 68, 69, 0,… (последовательность A046146 в OEIS )
Для простого n они равны
- 1, 2, 3, 5, 8, 11, 14, 15, 21, 27, 24, 35, 35, 34, 45, 51, 56, 59, 63, 69, 68, 77, 80, 86, 92, 99, 101, 104, 103, 110, 118, 128, 134, 135, 147, 146, 152, 159, 165, 171, 176, 179, 189, 188, 195, 197, 207, 214, 224, 223,… (последовательность A071894 в OEIS )
Количество примитивных корней по модулю n равны
- 1, 1, 1, 1, 2, 1, 2, 0, 2, 2, 4, 0, 4, 2, 0, 0, 8, 2, 6, 0, 0, 4, 10, 0, 8, 4, 6, 0, 12, 0, 8, 0, 0, 8, 0, 0, 12, 6, 0, 0, 16, 0, 12, 0, 0, 10, 22, 0, 12, 8, 0, 0, 24, 6, 0, 0, 0, 12, 28, 0, 16, 8, 0, 0, 0, 0, 20, 0, 0, 0, 24, 0, 24, 12, 0,… (последовательность A046144 в OEIS )
Для простого n это
- 1, 1, 2, 2, 4, 4, 8, 6, 10, 12, 8, 12, 16, 12, 22, 24, 28, 16, 20, 24, 24, 24, 40, 40, 32, 40, 32, 52, 36, 48, 36, 48, 64, 44, 72, 40, 48, 54, 82, 84, 88, 48, 72, 64, 84, 60, 48, 72, 112, 72, 112, 96, 64, 100, 128, 130, 132, 72, 88, 96,… (последовательность A008330 в OEIS )
Наименьшее простое число>n с примитивным корнем n равны
- 2, 3, 5, 0, 7, 11, 11, 11, 0, 17, 13, 17, 19, 17, 19, 0, 23, 29, 23, 23, 23, 31, 47, 31, 0, 29, 29, 41, 41, 41, 47, 37, 43, 41, 37, 0, 59, 47, 47, 47, 47, 59, 47, 47, 47, 67, 59, 53, 0, 53,… (последовательность A023049 в OEIS )
Наименьшее простое число (не обязательно превышающее n) с примитивным корнем n:
- 2, 3, 2, 0, 2, 11, 2, 3, 2, 7, 2, 5, 2, 3, 2, 0, 2, 5, 2, 3, 2, 5, 2, 7, 2, 3, 2, 5, 2, 11, 2, 3, 2, 19, 2, 0, 2, 3, 2, 7, 2, 5, 2, 3, 2, 11, 2, 5, 2, 3, 2, 5, 2, 7, 2, 3, 2, 5, 2, 19, 2, 3, 2, 0, 2, 7, 2, 3, 2, 19, 2, 5, 2, 3, 2,… (последовательность A056619 в OEIS )
Арифметические факты
Гаусс доказал, что для любого простого числа p (за исключением p = 3) произведение его первообразных корней сравнимо с 1 по модулю p.
Он также доказал, что для любого простого числа p сумма его примитивных корней сравнима с μ (p — 1) по модулю p, где μ — это функция Мёбиуса.
Например,
- p = 3, μ (2) = −1. Первообразный корень равен 2.
- p = 5, μ (4) = 0. Первоначальные корни равны 2 и 3.
- p = 7, μ (6) = 1. Примитивный корни равны 3 и 5.
- p = 31, μ (30) = -1. Первоначальные корни — это 3, 11, 12, 13, 17, 21, 22 и 24.
- Их произведение 970377408 1 (mod 31) и их сумма 123 ≡ −1 (mod 31).
-
- 3 × 11 = 33 ≡ 2
- 12 × 13 = 156 ≡ 1
- (−14) × (−10) = 140 ≡ 16
- (−9) × (−7) = 63 1 и 2 × 1 × 16 × 1 = 32 ≡ 1 (mod 31).
А как насчет сложения элементов этой мультипликативной группы? Как это бывает, суммы (или разности) двух примитивных корней складываются во все элементы подгруппы индекса 2 из Z / n Z для четного n и для всей группы Z / n Z, если n нечетное:
Z/ n Z+ Z/ n Z= Z/ n Z или 2 Z / n Z.
Поиск первообразных корней
Неизвестно простой общей формулы для вычисления первообразных корней по модулю n. Однако есть методы для поиска примитивного корня, которые быстрее, чем просто пробовать всех кандидатов. Если мультипликативный порядок числа m по модулю n равен φ (n) { displaystyle varphi (n)}

Сначала вычислите φ (n) { displaystyle varphi (n)}

- m φ (n) / pi mod n для i = 1,…, k { displaystyle m ^ { varphi (n) / p_ {i}} { bmod {n}} qquad { mbox {for}} i = 1, ldots, k}
с использованием быстрого алгоритма модульного возведения в степень, такого как возведения в степень возведением в квадрат. Число m, для которого все k результатов отличны от 1, является примитивным корнем.
Количество первообразных корней по модулю n, если они есть, равно
- φ (φ (n)) { displaystyle varphi left ( varphi (n) right)}
, поскольку, как правило, циклическая группа с r элементами имеет φ (r) { displaystyle varphi (r)}


Если g — примитивный корень по модулю p, то g также является примитивным корнем по модулю всех степеней p, если g ≡ 1 (mod p); в этом случае g + p равно.
Если g является примитивным корнем по модулю p, то либо g, либо g + p (в зависимости от того, какой из них нечетный) является примитивным корнем по модулю 2p.
Нахождение первообразных корней по модулю p также эквивалентно поиску корней (p − 1) циклотомического многочлена по модулю p.
Порядок величины примитивных корней
Наименьший примитивный корень g p по модулю p (в диапазоне 1, 2,…, p — 1) обычно маленький.
Верхние границы
Берджесс (1962) доказал, что для любого ε>0 существует C такое, что g p ≤ C p 1 4 + ϵ. { displaystyle g_ {p} leq Cp ^ {{ frac {1} {4}} + epsilon}.}
Гроссвальд (1981) доказал, что если p>ee 24 { displaystyle p>e ^ {e ^ {24}}}, затем gp < p 0.499 {displaystyle g_{p}

Carella (2015) доказал, что существует C>0 { displaystyle C>0}


Шоуп (1990, 1992) доказал, допуская обобщенную гипотезу Римана, что g p = O (log p).
Lo Наши границы
Фридландер (1949) и Сали (1950) доказали, что существует положительная постоянная C такая, что для бесконечного числа простых чисел g p>C log p.
Элементарно можно доказать, что для любого положительного целого числа M существует бесконечно много простых чисел, таких что M < gp< p − M.
Приложения
В часто используется примитивный корень по модулю n криптография, включая схему обмена ключами Диффи – Хеллмана. Рассеиватели звука были основаны на теоретико-числовых концепциях, таких как примитивные корни и квадратичные вычеты.
См. Также
- гипотеза Артина о примитивных корнях
- символ Дирихле
- Полное повторение простых чисел
- Обобщение Гаусса теоремы Вильсона
- Мультипликативный порядок
- Квадратичный вычет
- Корень из единицы по модулю n
Примечания
Ссылки
Пример 13.13
Для какого значения n группа 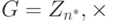
Решение
a. 
b. 
c. 
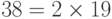
d. 
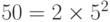
Если группа имеет примитивный корень, то обычно она имеет несколько таких корней. Число примитивных корней может быть вычислено как — 


Если группа G = < Z n* , x > имеет хотя бы один примитивный корень, то число примитивных корней — 

Рассмотрим три вопроса:
1. Если дан элемент a и группа 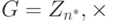
а. Мы должны найти 
б. Мы должны найти 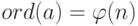
2. Если дана группа 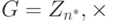
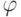
3. Если дана группа 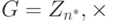

Циклическая группа. Циклические группы уже обсуждались в лекциях 5-6. Обратите внимание на то, что, если группа 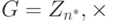
Пример 13.14
Группа 

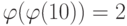
g = 3 -> g1 mod 10 = 3 g2 mod 10 = 9 g3 mod 10 = 7 g4 mod 10 = 1 g = 7 -> g1 mod 10 = 7 g2 mod 10 = 9 g3 mod 10 = 3 g4 mod 10 = 1
Обратите внимание, что группа 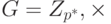
Группа G = < Zn*, x > является циклической группой, если она имеет примитивные корни. Группа G = < Zp*, x > всегда является циклической.
Идея дискретного логарифма. Группа 
- Её элементы включают все целые числа от 1 до p – 1.
- Она всегда имеет примитивные корни.
- Она всегда является циклической. Элементы могут быть созданы с использованием gx, где x — целое число от 1 до
.
- Примитивные корни можно представлять себе как основание логарифма. Если группа имеет k примитивных корней, то вычисления могут быть сделаны для k различных оснований. Данный x = logg y для любого элемента y в данном множестве, но есть другой элемент x, который является логарифмом y по основанию g. Этот тип логарифма называют дискретным логарифмом. Дискретный логарифм в литературе определяется несколькими различными символами, но мы будем использовать обозначение Lg, чтобы показать, что основание — g (сравнение по модулю).
Решение модульного логарифма с использованием дискретных логарифмов
Теперь рассмотрим, как решаются задачи типа y = ax (mod n), т. е. дано y, а мы должны найти x.
Табулирование дискретных логарифмов. Один из способов решения вышеупомянутой проблемы — использовать таблицу для каждого Zp* и различных оснований. Этот тип таблицы может быть предварительно рассчитан и сохранен. Например, таблица 13.4 показывает значения дискретного логарифма для Z7*. Мы знаем, что мы имеем два примитивных корня или основания в данном множестве.
| y | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| x = L3y | 6 | 2 | 1 | 4 | 5 | 3 |
| x = L5y | 6 | 4 | 5 | 2 | 1 | 3 |
Составив таблицы для других дискретных логарифмов для всех групп и всех возможных оснований, мы можем решить любую дискретную логарифмическую проблему. Этот подход подобен изучаемым в прошлом традиционным логарифмам. До появления калькуляторов и компьютеров таблицы использовались, чтобы вычислять логарифмы по основанию 10.
Пример 13.15
Найдите x в каждом из следующих случаев:
a.
b.
Решение
Мы можем легко использовать таблицу 13.4 дискретного логарифма.
a.
b.
Использование свойств дискретных логарифмов. Чтобы показать, что дискретные логарифмы ведут себя точно так же, как традиционные логарифмы, в таблице 13.5 приводится несколько свойств обоих типов логарифмов. Обратите внимание, что основание модуля — 
Использование алгоритмов, основанных на дискретных логарифмах. Таблицы и свойства дискретных логарифмов не могут быть использованы для решения уравнения y = a x (mod n), когда n является очень большим. Для решения этой проблемы были разработаны несколько алгоритмов, в которых используется основная идея дискретных логарифмов. Хотя все эти алгоритмы более эффективны, чем алгоритмы полного перебора, которые мы упоминали в начале этого раздела, но ни один из них не имеет полиномиальную сложность. Большинство этих алгоритмов имеет такой же уровень сложности, как проблема разложения на множители.
Проблема дискретного логарифма имеет такую же сложность, как проблема разложения на множители.
В поле Галуа первообразным корнем степени n из единицы называется элемент
$ mathfrak a $, который удовлетворяет условиям
$$ mathfrak a^n=mathfrak e , mathfrak a^k ne mathfrak e quad npu quad kin {1,2,dots,n-1} . $$
Будем также говорить, что $ mathfrak a $ принадлежит показателю n.
Т
Теорема 1. В поле Галуа $ mathbf{GF} (p^m) $ существуют первообразные корни степени $ p^m-1 $ из единицы.
В поле $ mathbf{GF} (p^m) $ первообразный корень степени $ p^m-1 $ из единицы называется примитивным элементом поля.
Лемма 1. Пусть $ mathfrak a in mathbf{GF} (p^m), mathfrak a ne mathfrak o $ — первообразный корень степени $ n_{} $ из единицы. Тогда $ p^m-1 $ делится на $ n_{} $.
Доказательство. Если $ p^m-1 $ не делится на $ n_{} $, т.е.
$$ p^m-1 = nq+ r quad npu quad {r,q} subset mathbb N quad u 0< r< n , $$
то одновременно выполняется и $ mathfrak a^n=mathfrak e $ и $ mathfrak a^{p^m-1}=mathfrak e $
( обобщенная теорема Ферма ). Тогда
$$ mathfrak a^r=mathfrak a^{(p^m-1)-nq}=mathfrak a^{p^m-1} cdot left( mathfrak a^{nq} right)^{-1} = mathfrak e cdot mathfrak e = mathfrak e ,
$$
т.е. $ mathfrak a $ является корнем из единицы степени меньшей $ n_{} $.
♦
Обозначим $ psi (n) $ — число элементов поля $ mathbf{GF} (p^m) $, принадлежащих показателю $ n_{} $. Согласно лемме 1, число $ n_{} $ должно быть делителем числа $ p^m-1 $. Кроме того, если $ {1,d_1,d_2,dots, p^m-1} $ — множество всех делителей числа $ p^m-1 $, то
$$ psi (1)+psi(d_1)+psi(d_2)+dots+psi(p^m-1) = p^m-1 , $$
поскольку любой элемент поля принадлежит одному и только одному показателю.
Лемма 2. Если $ mathfrak a $ принадлежит показателю $ n_{} $ и число $ k_{} $ взаимно просто с $ n_{} $, то и $ mathfrak a^k $ принадлежит показателю $ n_{} $.
Доказательство. В самом деле, $ left( mathfrak a^{k} right)^n = left( mathfrak a^{n} right)^k = mathfrak e $. С другой стороны, при $ n_1 < n $ равенство $ left( mathfrak a^{k} right)^{n_1} = mathfrak e $ невозможно. В самом деле, если оно все же выполнено при $ k_{} $ взаимно простом с $ n_{} $. Тогда, существуют целые числа $ u_{} $ и $ v_{} $, обеспечивающие выполнение равенства $ u,k+v, n =1 $. Возведем равенство $ left( mathfrak a^{k} right)^{n_1} = mathfrak a^{kn_1} = mathfrak e $ в степень $ u_{} $:
$$ mathfrak e = mathfrak a^{kun_1} = mathfrak a^{n_1} mathfrak a^{n_1(ku-1)} =
mathfrak a^{n_1} mathfrak a^{-vnn_1} = mathfrak a^{n_1} ,
$$
т.е. $ mathfrak a $ является корнем из единицы степени меньшей $ n_{} $.
♦
Итак, при любом $ k<n $ таком, что $ operatorname{HOD} (k,n)=1 $, элементы $ mathfrak a^k $ принадлежат показателю $ n_{} $, если $ mathfrak a $ принадлежит этому показателю. С другой стороны, множество
$$ { mathfrak a^k mid kin {1,dots,n-1}, operatorname{HOD} (k,n)=1 } $$
содержит все элементы, принадлежащие показателю $ n_{} $, поскольку множество
$$ { mathfrak a^k mid kin {0,dots,n-1} } $$
содержит все решения уравнения $ mathfrak x^n= mathfrak e $; а при условии
$ operatorname{HOD} (k,n)>1 $ элемент $ mathfrak a^k $ принадлежит показателю меньшему, чем $ n_{} $ (см. аналогию с первообразными корнями из единицы в поле комплексных чисел ). Число элементов в первом из этих множеств известно — оно равно значению
функции Эйлера от числа $ n_{} $, т.е. $ phi (n) $. Таким образом, для любого числа $ n in mathbb N $ будет либо $ psi(n)=0 $, либо $ psi(n) = phi (n) $, т.е., в общем случае,
$$ psi(n) le phi(n) . $$
Лемма 3. Если $ p^m-1 $ делится на $ n_{} $, то $ psi (n) = phi (n) $.
Доказательство. Если $ {1,d_1,d_2,dots, p^m-1} $ — множество всех делителей числа $ p^m-1 $, то, с одной стороны, имеем выведенное выше равенство:
$$ psi (1)+psi(d_1)+psi(d_2)+dots+psi(p^m-1) = p^m-1 ; $$
с другой же стороны, для функции Эйлера справедливо аналогичное равенство
$$
phi (1)+phi(d_1)+phi(d_2)+dots+phi(p^m-1) = p^m-1 .
$$
Вычитаем из второго первое:
$$
sum_{d} left[ phi (d) — psi (d) right] =0 ,
$$
где суммирование идет по всем числам $ d_{} $, являющимися делителями числа $ p^m-1 $. Каждое слагаемое — по неравенству, выведенному выше, — неотрицательно. Следовательно, оно должно равняться нулю.
♦
Доказательство теоремы 1 следует из леммы 3 при $ n=p^m-1 $. Фактически мы получили и точное значение для количества первообразных корней степени $ p^m-1 $ из единицы, т.е. для количества примитивных элементов поля $ mathbf{GF} (p^m) $ — оно равно
$$ phi (p^m-1) . $$
♦
Как найти примитивный элемент поля?
Воспользуемся аналогией этого объекта с первообразным корнем по модулю простого числа $ p_{} $ из раздела
☞
ИНДЕКС (дискретный логарифм).
Т
Теорема 2. Если каноническое разложение числа $ p^m-1 $ имеет вид:
$$
p^m-1=p_1^{{mathfrak m}_{_1}}p_2^{{mathfrak m}_{_2}}times dots times p_{mathfrak r}^{{mathfrak m}_{_{mathfrak r}}}
,
$$
то для того чтобы элемент $ mathfrak A in mathbf{GF} (p^m) $, был примитивным элементом этого поля, необходимо и достаточно, чтобы
$$
mathfrak A^{(p^m-1)/p_j} notequiv mathfrak e quad npu quad forall jin {1,dots, mathfrak r}
.
$$
Доказательство аналогично доказательству теоремы 5 из пункта
☞
ПЕРВООБРАЗНЫЙ КОРЕНЬ.
♦
П
Пример. Будет ли полином $ x^3+x^2 $ примитивным элементом поля $ mathbf{GF}(16) $, если операция умножения в этом поле определена по двойному модулю $ 2, x^4+x^3+x^2+x+1 $?
Решение. Имеем $ 2^4-1=15=3cdot 5 $.
$$ (x^3+x^2)^{15/3} equiv_{2} x^{15}+x^{14}+x^{11}+x^{10} equiv x^3+x^2+1 notequiv 1 quad (operatorname{modd} 2,x^4+x^3+x^2+x+1) ;
$$
$$ (x^3+x^2)^{15/5} equiv_{2} x^9+x^8+x^7+x^6
equiv 1 quad (operatorname{modd} 2,x^4+x^3+x^2+x+1) .
$$
Ответ. Нет.
Лемма 2 позволяет найти все семейство примитивных элементов поля, если один уже обнаружен.
Т
Теорема 3. Если $ mathfrak A in mathbf{GF} (p^m) $ — примитивный элемент поля, то $ mathfrak A^k $ будет примитивным элементом поля тогда и только тогда, когда показатель $ k_{} $ взаимно прост с $ p^m-1 $: $ operatorname{HOD} (k,p^m-1)=1 $.
П
Пример. Определить все примитивные элементы поля $ mathbf{GF}(16) $, если операция умножения в этом поле определена по двойному модулю $ 2, x^4+x^3+1 $.
Решение. С помощью теоремы 2 устанавливаем, что полином $ x_{} $ является примитивным элементом поля. Но тогда, в соответствии с теоремой 3, полиномы
$$ x^2,x^4, x^7equiv x^2+x+1, x^8equiv x^3+x^2+x, x^{11} equiv x^3+x^2+1, x^{13}equiv x^2+x, x^{14}equiv x^3+x^2 quad (operatorname{modd} 2,x^4+x^3+1)
$$
также должны быть также примитивными элементами поля. Их (вместе с $ x_{} $) как раз $ phi(15)=8 $ штук, так что больше примитивных корней нет.
♦
?
Будет ли полином $ x_{} $ примитивным элементом поля $ mathbf{GF}(2^8) $, если операция умножения в этом поле определена по двойному модулю
a) $ 2, x^8+x^4+x^3+x^2+1 $;
b) $ 2, x^8+x^4+x^3+x+1 $?
Материалы этого пункта взяты (с незначительными модификациями) из
[1]. Чеботарев Н. Основы теории Галуа. Часть I. М.-Л.ОНТИ.1934






















































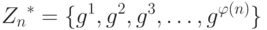
 .
.