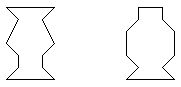Как найти приближенное значение площади фигуры - Avtoru.top

Довольно точно можно вычислить площадь прямоугольной фигуры, но для фигуры неправильной формы можно найти её приближённую площадь. Для этого удобно использовать палетку.

Палетка — это прозрачная плёнка (или калька), расчерченная на равные квадраты со стороной (1) см.

Самостоятельно сделай палетку.

С её помощью ты сможешь быстро находить приближённую площадь разных фигур.

Для нахождения приближённой площади фигуры нужно:

1) наложить палетку на фигуру;

2) посчитать число (a) целых клеток внутри фигуры;

3) посчитать количество (b) клеток, частично входящих в фигуру;

4) вычислить приближённую площадь

S≈a+b:2

Поясним также, зачем нужно делить (b) на два.

(b) — число клеток, частично входящих в фигуру. У одних большая часть входит в фигуру, у других — меньшая. Из них можно составить приближённо (b:2) полных клеток (если (b) нечётно, то можно сначала увеличить (b) на (1), а потом уже разделить на (2)).

Обрати внимание!

Для записи приближённого равенства используется знак

≈

Найдём с помощью палетки приближённую площадь фигуры (B) неправильной формы.

1. Наложим палетку на фигуру (B).

2. Посчитаем количество (a) клеток, целиком находящихся внутри фигуры (закрашены зелёным цветом):

3. Посчитаем количество (b) клеток, частично входящих в фигуру (B) (закрашены синим). Таких клеток (17) — это нечётное число, поэтому увеличим это число на (1) и поделим на (2):

17+1=18,18:2≈9.

4. Сложим числа, полученные в пунктах (2) и (3), и запишем приближённую площадь фигуры (B):

S≈16+9=25см2.

Обрати внимание!

Нужно понимать разницу между оценкой площади и нахождением её приближённого значения!

Оценка площади записывается неравенством

a<S<b

Приближённое значение площади — это число, которое можно найти по формуле

S≈a+b:2

Источники:

Изображение: палетка. © ЯКласс.
Изображения: фигура. © ЯКласс.

Источник

Урок 18. Приближенное вычисление площадей

Гипермаркет знаний>>Математика>>Математика 4 класс>> Урок 18. Приближенное вычисление площадей

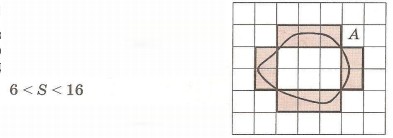
Сколько места занимает фигура А на плоскости? Другими словами, какова ее площадь?

Ответ на этот вопрос мы можем дать лишь приблизительно, указав границы, в которых находится площадь фигуры А:

Какое же число из указанного промежутка наиболее точно выражает фигуры?
Внутри фигуры А расположены 6 целых клеток, а остальные 10 клеток входят в нее частично: иногда меньшая часть клетки, а иногда — большая. Поэтому всего в фигуре А содержится примерно

6 + 10 :2 = 6 + 5 = 11 квадратных единиц (6 < 11 < 16). Это записывают с помощью знака приближенного равенства ««

S . 11 кв. ед.

Читают: «Площадь приближенно равна 11 квадратным единицам».

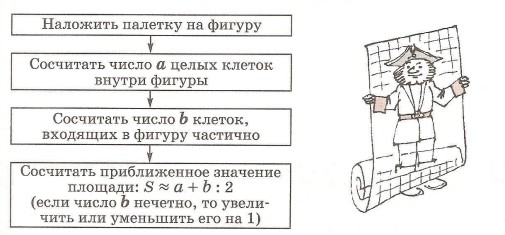
Инструмент, с помощью которого находят приближенное значение площади, называется палеткой. Это калька (или прозрачная пленка), разбитая на квадратные сантиметры. Вычисление площади с помощью палетки выполняется по следующему алгоритму.

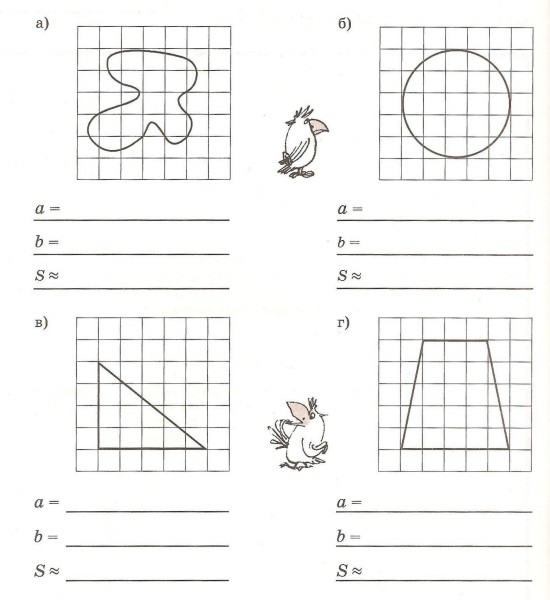
1. На фигуры наложены палетки. Вычисли площадь фигур, если площадь каждой клетки равна 1 см².

2. Наложи кальку на клетчатуб бумагу и сделай палетку . Нарисуй на листе бумаги какую-нибудь замкнутую линию и найди приближенно площадь фигуры, ограниченной этой линией.

3. Начерти циркулем окружность радиусом 4 см и найди с помощью палетки площадь получившегося круга.

4. Виктормна «Хочу все знать».

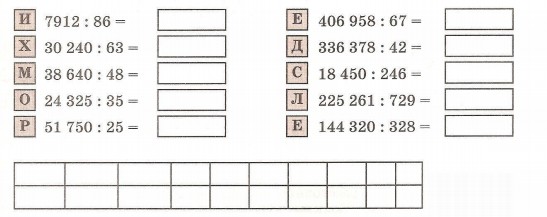
а) На островах Тихого океана живут черепахи-гиганты. Они такой величины, что дети могут кататься, сидя у них на панцире. Расшифруй название самой крупной в мире черепахи, расположив ответы примеров в порядке убывания.

б) Эта черепаха прекрасно плавает, ее конечности превратились в ласты. Найди массу черепахи-гиганта в килограммах, сосчитав сумму корней двух уравнений:

(х • 6 — 956) : 4 = 70 328 — (у + 6) : 4 = 228.

в) Вырази массу черепахи в центнерах, в граммах. Какие еще единицы массы ты знаешь?

5. а) Выполни деление:

27 506 : 10 = ———————

27 506 : 100 = ———————

27 506 : 1000 = ———————

б) Вырази в новых единицах счета и измерения:

Что ты замечаешь?

6. Придумай выражения, значение которых равно 96.

7. Придумай задачу, которая решается так: а + а • 3 + (а — 5).

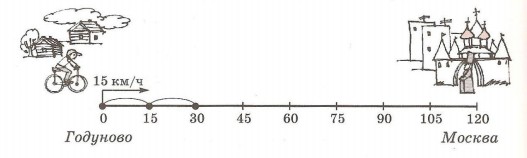
8. а) Из деревни Годуново в Москву выехал велосипедист со скоростью 15 км/ч. Расстояние от Годунова до Москвы равно 120 км. Покажи движение велосипедиста на числовом луче и определи, на каком расстоянии от Годунова и от Москвы был он через 3 ч после выезда? Через 7 ч? Через сколько времени он прибыл в Москву?

б) Пусть S км — расстояние, пройденное велосипедистом, а d км — его расстояние до Москвы. Заполни таблицу и запиши формулы, выражаюш,ие зависимость величин s и d от времени t. Какие значения может принимать в этих формулах переменная t?

9. Автобус проехал расстояние 480 км за 8 ч. За сколько времени пройдет это расстояние автомобиль, скорость которого на 36 км/ч больше скорости автобуса? С какой скоростью надо ехать, чтобы преодолеть это расстояние за 4 часа?

10. а) 90 412 — 128 • 84 : (6040 — 5848) • 370 + 53 878 • 0;

б) 4800 • 74 — (506 — 399) • 301 + 30 075 : 15 • 42.

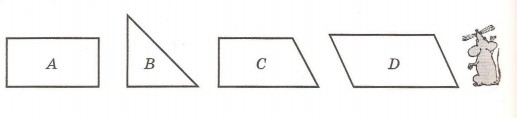
11*. Для каждой фигуры на рисунке объясни, почему она лишняя:

Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 1. — М.: Издательство «Ювента», 2005, — 64 с.: ил.

_{Календарно-тематическое планирование по математике, задачи и ответы школьнику онлайн, курсы учителю по математике скачать}

Содержание урока
 конспект урока
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.

Разработка — Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email:

Источник

§1. Оценка площади

В этом уроке ответим на вопрос: как произвести оценку площади? А также научимся выполнять приближённое вычисление площади.

Давайте представим ситуацию.

Однажды ученики 4 класса побывали на кондитерской фабрике. Им показывали, как делают вафли. В конце экскурсии кондитер отломил каждому ученику от большой пластины по маленькому кусочку хрустящей вафли. Кусочки были неодинаковые. Петя и Вася стали спорить, чей кусок оказался больше.

Как же им помочь решить их спор? Можно конечно сравнить, наложив один кусок на другой. Но сравнение точным не получится, так как одну из фигур разместить внутри другой нельзя.

Какой же метод сравнения используют в случае, когда наложением сравнить нельзя? Конечно, нужно сделать измерения. Чтобы измерить площадь фигуры, нужно выбрать единицу измерения и определить, сколько раз она содержится в фигуре.

Единицы измерения площади – это квадратный миллиметр, квадратный сантиметр, квадратный метр, квадратный километр.

На рисунке мы видим, что вафли разделены на квадраты. Возьмём их за единицу измерения площади вафель. На рисунке также видно, что площадь вафель состоит из целых и нецелых квадратов.

Определим, между какими числами заключена площадь каждой вафли, т.е. сделаем оценку площади, найдём «нижнюю и верхнюю границы».

«Нижняя граница» – это меньшее число квадратов, значит, мы будем считать только целые квадраты внутри фигуры. Чтобы найти «верхнюю границу», нужно найти большее число квадратов. Значит, нужно найти количество всех целых и всех нецелых квадратов вместе.

Итак, давайте сделаем оценку площади Петиной вафли.

Сосчитаем целые квадраты, их получилось 8. Это «нижняя граница» площади.

Сосчитаем все нецелые квадраты фигуры, их – 2, прибавим к целым, получилось 10. Это «верхняя граница» площади.

Значит, площадь Петиной вафли находится в границах от 8 до 10 квадратов. Это можно записать в виде двойного неравенства.

8 < S < 10

Теперь сделаем оценку площади Васиной вафли. Считаем все целые квадраты внутри фигуры, «нижняя граница» – 8. Считаем все нецелые квадраты фигуры и добавляем к целым, «верхняя граница» – 11. В результате мы получаем следующее неравенство, которое обозначает «нижнюю и верхнюю границы» площади Васиной вафли.

8 < S < 11

Таким образом, у нас получилось, что у мальчиков почти одинаковые по площади вафли.

Давайте обобщим, чтобы произвести оценку площади надо:

1. сосчитать число целых квадратов, расположенных внутри фигуры, то есть определить «нижнюю границу» площади.

2. сосчитать число нецелых квадратов фигуры и прибавить к ним количество всех целых квадратов, расположенных внутри фигуры, то есть определить «верхнюю границу» площади.

3. записать двойное неравенство, указав «верхнюю» и «нижнюю» границы площади.

§2. Приближенное вычисление площадей

А теперь вычислим площадь этих вафель.

Внутри вафель мы можем насчитать 8 целых квадратов. Остальные квадраты входят частично, поэтому число нецелых квадратов делим пополам. Итак, в Петиной вафле содержится 8 целых и 2 нецелых квадрата.

Значит, примерно 8 + 2 : 2 = 8 + 1 = 9 квадратов. (8 < 9 < 10).

В Васиной вафле содержится 8 целых и 3 нецелых квадрата.

Значит, 8 + 3 : 2. Так как число 3 нечётное и на 2 не разделится, его нужно увеличить на 1. Давайте 3 увеличим на 1, получим 8 + 4 : 2 = 8 + 2 = 10 квадратов. (8 < 10 < 11).

Так как мы можем посчитать количество квадратов только приблизительно. Мы не имеем право ставить знак «=» между найденным количеством квадратов и площадью. Поэтому для обозначения примерного результата используем знак приближенного равенства «≈».

S ≈ 9 ед2

S ≈ 10 ед2.

Читать следует так:

«Площадь приближенно равна 9 квадратным единицам».

«Площадь приближенно равна 10 квадратным единицам».

Таким образом, мы выполнили приближенное вычисление площади вафель Пети и Васи.

Вычислить приблизительную площадь вафель мы смогли благодаря тому, что фигуры были разделены на квадраты.

Что делать, если таких квадратов нет? Самим расчерчивать фигуры очень долго, поэтому люди придумали особое приспособление – палетку.

Палетка – прозрачная плёнка, разделённая на одинаковые квадраты.

Вычислим площадь фигуры при помощи палетки,

площадь каждой клетки которой равна 1 см2.

1. Наложим палетку на фигуру.

2. Сосчитаем число целых клеток внутри фигуры (а = 6).

3. Сосчитаем число клеток входящих в фигуру частично (b = 14).

4. Вычислим приближенное значение площади 6 + 14 : 2 = 6 + 7 = 13, S ≈13 см2.

Для вычисления приближенного значения площади используют формулу S ≈ а+b:2, где a — это число целых клеток, b – число нецелых клеток.

§3. Краткие итоги урока

Для того чтобы произвести оценку площади, необходимо:

1. Сосчитать число целых квадратов, расположенных внутри фигуры, то есть определить «нижнюю границу» площади.

2. Сосчитать число нецелых квадратов фигуры и прибавить к ним количество всех целых квадратов, расположенных внутри фигуры, то есть определить «верхнюю границу» площади.

3. Записать двойное неравенство, указав «верхнюю» и «нижнюю» границы площади.

Для того чтобы вычислить площадь фигуры при помощи палетки, необходимо:

1. Наложить палетку на фигуру.

2. Сосчитать число а целых клеток внутри фигуры.

3. Сосчитать число b клеток, входящих в фигуру частично.

4. Вычислить приближенное значение площади: S ≈ а + b : 2 (если число b нечётно, то увеличить его на 1).

Источник

Цели урока:

Закрепить умение находить площадь
прямоугольника и квадрата.
Учить искать приближённое значение площади
фигур с помощью палетки, построить
соответствующий алгоритм действий.
Развивать критическое мышление, речь,
воображение, интерес к математике.

Оборудование урока:

Демонстрационный материал (палетка с кв. дм,
фигуры ваз, карточки для устного счёта в виде кв.
дм,
Таблицы “Знаю, хочу узнать, узнал”, карточки с
фигурами для групповой работы, палетки.

Ход урока

I. Организационный момент.

— Урок математики я начну со стихотворения.

Математика – королева наук!
Без неё не летят корабли,
Без неё не поделить ни акра земли,
Даже хлеба не купишь, рубля не сочтёшь,
Что по чём не узнаешь,
А узнав, не поймёшь.

— Для чего мы изучаем эту науку?

— Сегодня на уроке будет очень интересный, но
трудный материал. И подготовиться к его изучению
нам поможет устный счёт.

II. Стадия вызова.

Устный счёт. Игра “Молчанка”.

(На кв. дм – задания, ученики воспринимают их
зрительно, считают устно, записывают в тетрадях
ответы).

13 x 6	2 x m = 72
52 : 2 x 8	x : 6 = 70
570 — 450	y + 140 = 500
600 : 5	430 — b = 208
170 x 4	а = 17дм, в = 4дм, Sпр. = ?
	а = 11см, Sкв. = ?

— Проверка (один ученик зачитывает ответы, на
доске одновременно выкладывается фигура из кв.
дм с правильными ответами:

— Найдите среди ответов лишнее число. Почему оно
лишнее? (121см², т.к. оно нечётное)

— Какие числа мы называем чётными?

— Какие чётные числа можно получить, используя
число 121 и как это можно сделать?

(На доске появляется таблица-опора:

— На что похожа получившаяся на доске фигура?
(цифра 5, обозначение пути или площади).

— Какова площадь этой фигуры? (11дм²)

— Слово площадь – многозначное. Какие же
значения имеет это слово? Обратимся к словарю
Ожегова. (Один ученик зачитывает значения слова
площадь.)

— Сегодня мы будем говорить о математическом
значении слова площадь.

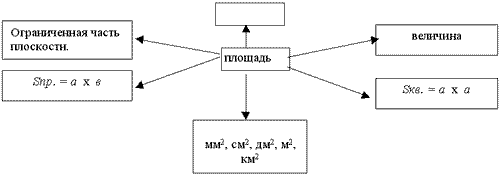
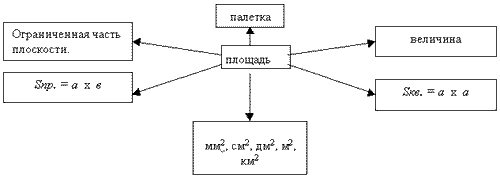
(На доске появляется кластер. Закрыты
все главные слова, кроме слова площадь).

Работа с таблицей “Знаю, хочу узнать, узнал”.

— Вспомним всё, что мы знаем о понятии площадь.
Напишите это в первой графе таблицы — “Знаю”.

— Обсудите всё, что вы написали в парах, … в
группах. (Заслушиваются ответы нескольких
учеников. В кластере открываются записи в
прямоугольниках.)

— Расскажите о площади, используя кластер.

— Что бы вы ещё хотели узнать о площади? Запишите
во второй графе таблицы “Знаю, хочу узнать,
узнал”.

(Выслушиваются предложения нескольких
учеников, которые записываются в краткой форме
на доске в графе “Хочу узнать”).

Групповая работа, постановка проблемы.

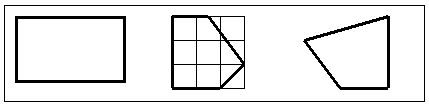
— Найдите площадь первой фигуры, оцените
площадь второй фигуры, найдите площадь третьей
фигуры.

Проверка выполненных заданий.

— Какова площадь первой фигуры? (18 см²).

Что значит оценить площадь? (Оценить площадь
фигуры – значит найти нижнюю и верхнюю границы
значения площади.)

Как находили границы площади? (Нижняя граница –
число целых квадратиков внутри фигуры, верхняя
граница – число целых квадратиков + число
нецелых квадратиков внутри фигуры.)

Кто вычислил площадь третьей фигуры? Как?
(Возможно дети делили фигуру на квадраты и
оценивали её площадь).

А как сделать так, чтобы при нахождении площади
фигуры не разделять её на квадраты, не тратить на
это время? (Дети могут предложить
воспользоваться уже готовым квадратом,
разделённым на квадратные единицы. Учитель
показывает такой квадрат, но непрозрачный. )

Возможно с помощью этого приспособления найти
площадь фигуры? (Нет, т.к. самой фигуры не видно.
Ученики делают вывод о том, что такой квадрат
должен быть прозрачным.)

Действительно, существует специальный
инструмент, который сэкономит драгоценное время
при нахождении площади фигур. Это палетка. (
Демонстрируется палетка, в кластере открывается
это слово.)

— Рассмотрите фигуры на доске.

— Как можно сравнить площади этих фигур? Можем
ли мы найти точное значение площади

каждой фигуры? Так как мы не можем найти точное
значение площади, тогда какое

значение мы можем найти? (приближённое)

Объявление темы урока, постановка учебной
задачи.

— “Приближённое вычисление площадей”.

— Задайте вопросы к теме урока. (Вопросы кратко
записываются учителем во вторую графу таблицы –
“Хочу узнать”.)

— Какова наша учебная задача на этом уроке?
(Научиться находить приближённое значение
площади фигуры.)

Стадия осмысления.

— Какие шаги нужно сделать, чтобы найти
приближённое значение площади каждой вазы?

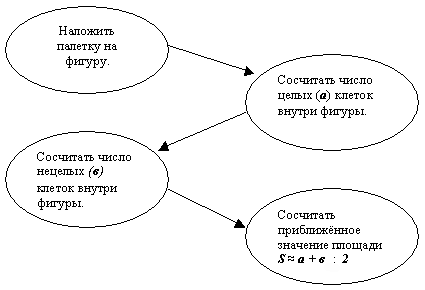
Составление алгоритма действий.

(На доске открывается вторая шаг алгоритма.)

-Каким должен быть первый шаг? (Наложить палетку
на фигуру).

— Сосчитайте число целых клеток внутри фигуры.

— Что сделаем дальше? (Сосчитаем число нецелых
клеток внутри фигуры).

— Предположите, какой будет следующий шаг.
(Ученики могут предложить два варианта: к числу
целых клеток внутри фигуры прибавить число
нецелых клеток или к числу целых клеток
прибавить число нецелых клеток, делённое на 2, т.
к. у нецелых клеток в фигуру входят или половина,
или меньшая часть, или большая).

-Проверим свои предположения по учебнику.
Почему не подходит первый вариант?

(В алгоритме открывается четвёртый шаг.)

— При каком условии мы можем воспользоваться
формулой приближённого вычисления площади? (в
– чётное число.)

— Что нужно сделать, если при подсчёте клеток в
оказалось нечётным числом? (+или- единицу.)

Стадия рефлексии.

Вычисление площадей демонстрационных фигур.

Самостоятельная практическая работа в группах.

— Вычислите приближённое значение площади
четвёртой фигуры с помощью палетки.

Проверка выполненного задания.

Подведение итога, самооценка.

— Прочитайте ещё раз тему нашего урока. Оцените
себя с помощью цветового сигнала, на сколько
хорошо вы поняли эту тему.

— Запишите в третьей графе таблицы “Знаю, хочу
узнать, узнал” всё то новое, что вы узнали
сегодня на уроке в соответствии с темой.

— Чтобы обобщить наши знания о площади,
воспользуемся синквейном. Вставьте недостающие
слова.

Значение S.
Точное, приближённое.
Находить, вычислять, оценивать.
Используют формулы, палетку.
Величина.

Источник

Приближенное значение площади фигуры, изображенной на квадратной сетке, можно найти по следующему алгоритму:
Отметь все квадраты, большая часть которых попала внутрь фигуры.
Подсчитать их количество.
Определить площадь одного квадрата.
Умножить число квадратов на площадь одного квадрата сетки.
Начертите на листе в клетку замкнутую линию без самопересечений. Пользуясь описанным алгоритмом, найдите площадь фигуры, ограниченной вашей линией.