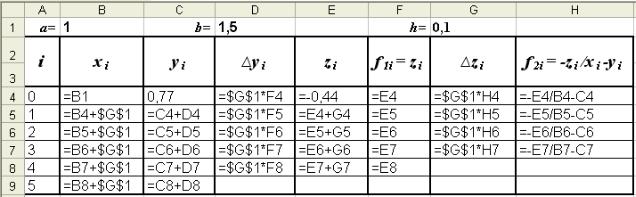
Режим решения Рис. 3.2 – а
Рассмотрим некоторые методы численного решения уравнений вида
где f(x) – заданная алгебраическая или трансцендентная функция действительного аргумента x; в первом случае уравнение называется алгебраическим, во втором – трансцендентным.
Известно, что не всякое уравнение решается точно, и, прежде всего, это относится к большинству трансцендентных уравнений. Известно также, что нельзя точно решить произвольное алгебраическое уравнение степени выше четвертой. Но, поскольку точное решение уравнения в большинстве случаев не требуется, считают, что задача отыскания корней решена, если их значения определены с требуемой степенью точности.
Задача ставится следующим образом:
Дано уравнение f(x) = 0, где f(x) – непрерывная функция в некоторой области. Корни этого уравнения x* — те значения аргумента x, которые обращают уравнение в тождество. Найти приближенное значение корня x* с точностью ε означает указать интервал длиной не более ε, содержащий точное значение корня x.
При отыскании приближенных значений корней уравнения приходится решать две задачи:
1)отделение корней, т.е. выделение интервалов из области непрерывности функции, в каждом из которых заключен только один корень уравнения;
2)уточнение корня, т.е. построение итерационного процесса, позволяющего сузить границы выделенного интервала до значения заданной точности.
4.1. Отделение корней
Графический метод отделения корней
При графическом методе строят график функции для уравнения вида f(x) = 0 или представляют уравнение в виде φ(x) = ψ(x) и строят графики функций y = φ(x) и y = ψ(x). Значения действительных корней уравнения являются абсциссами точек пересечения функции y = f(x) с осью х или абсциссами точек пересечения графиков функций y = φ(x) и y = ψ(x). Отрезки, в которых заключено только по одному корню, легко находятся.
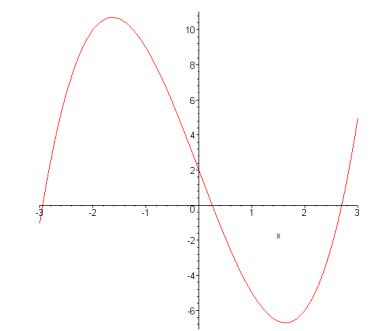
Пример 4.1. Отделить корни уравнения x3 — 8x + 2 = 0 графическим методом,
где x [-3, 3].
1) Построим график функции y = x3 -8 x + 2 (рис. 4.1).
|
Рис. 4.1 |
|
|
Корни находятся на интервалах [-3; -2], [0; 1] |
и [2; 3]. |
|
2) Представим уравнение x3 — 8x + 2 = 0 в виде |
x3 = 8x – 2. Построим графики |
функций y = x3 и y1 = 8x – 2 (рис. 4.2). Значениями действительных корней урав-
нения x3 — 8x + 2 = 0 являются абсциссы точек пересечения графиков функций y = x3 и y1 = 8x – 2.
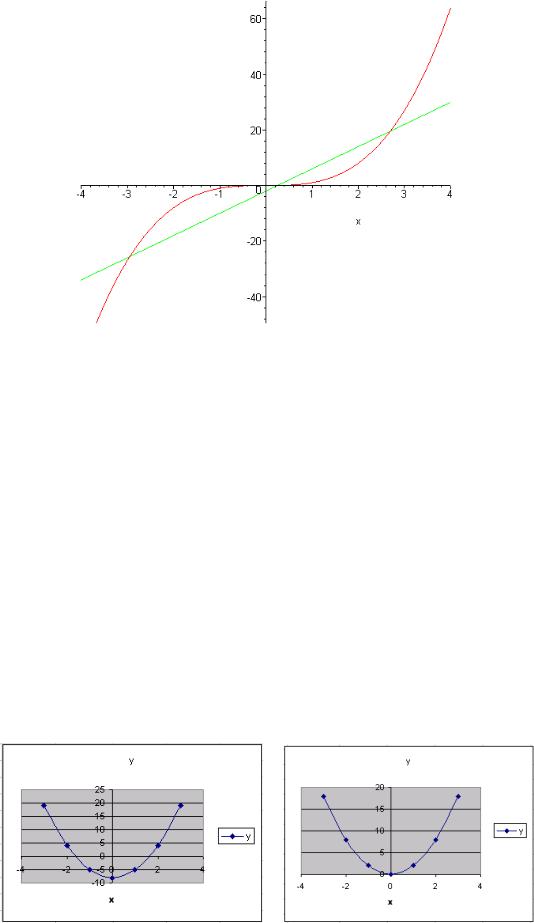
Рис. 4.2
Корни находятся на интервалах [-3; -2], [0; 1] и [2; 3].
Аналитический метод отделения корней
Для отделения действительных корней непрерывных функций следует помнить следующее:
Если функция f(x) непрерывна на интервале [a, b] и имеет на концах интервала [a, b] одинаковые знаки (т.е. f(a)·f(b) > 0), то на этом интервале имеется четное число корней или их нет (рис. 4.3);
!нельзя забывать, что корнем функции может быть не только точка пересе-
чения графика функции f(x) с осью x, но и его касание с осью x (рис. 4.4). В случае, показанном на рис. 4.4, при x = 0 монотонность функции нарушается.
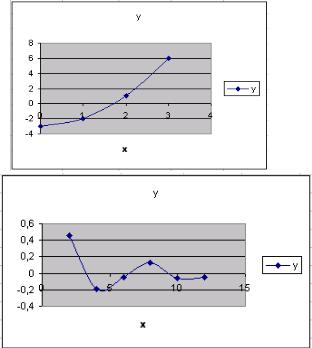
Если функция f(x) непрерывна на интервале [a, b] и имеет на концах интервала [a, b] разные знаки (т.е. f(a)·f(b) < 0), то на этом интервале имеется нечетное число корней (рис. 4.5, 4.6);
! разные знаки функции на концах интервала указывают на наличие корня на интервале [a, b], но не гарантируют его единственности.
Если функция f(x) непрерывна на интервале [a, b], монотонна и ее значения на концах интервала имеют разные знаки (f(a)·f(b) < 0), то уравнение на этом интервале имеет единственный корень.
Из этого следует, что для единственности корня на участке [a, b] достаточ-
но, чтобы выполнялись условия: f(a)·f(b) < 0, а f’(x) была знакопостоянна для любого x, принадлежащего [a, b].
! иногда для единственности корня бывает достаточно и знакопостоянства второй производной.
Таким образом, чтобы отделить все корни уравнения, следует:
найти промежуток, где f(a)·f(b) < 0, а f’(x) или f»(x), или и f’(x), и f»(x) были знакопостоянны;
отыскать нули и точки разрыва f’(x) и проверить, не являются ли они корнями уравнения.
Пример 4.1 (продолжение). Отделить все действительные корни уравнения
(4.1) на отрезке [-3, 3]:
f(x) = x3 — 8x +2 = 0.
Решение.
Вычислим значения функции f(x) на концах отрезка [-3, 3]:
f(-3) = (-3)3 — 8·(-3) + 2 = -1, f(3) = (3)3 — 8·3 + 2 = 5.
f(-3)·f(3) < 0, поэтому на отрезке [-3, 3] имеется или один корень, или нечетное число корней.
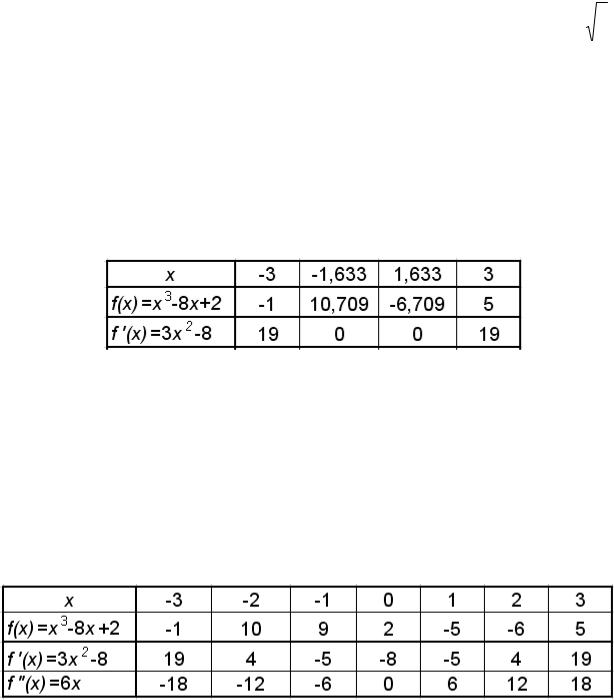
f’(x) = 3x2 — 8 – непрерывна, поэтому для определения интервалов монотонности f(x) найдем значения x, при которых f’(x) = 0. f’(x) = 3x2 – 8 = 0 при x = 83 ≈
±1,633.
Таким образом, можно отделить следующие интервалы монотонности функции f(x): [-3; -1,633], [-1,633; 1,633], [1,633; 3] и на каждом из этих ин-
тервалов отделено по одному корню уравнения.
Для наглядности вычислим значения f(x) и f’(x) на концах этих промежутков (табл. 4.1). f’(x) = 3x2 – 8.
Таблица 4.1
Другие методы отделения корней
Для отделения корней можно использовать табулирование функции f(x), задав некоторые значения аргумента на рассматриваемом промежутке (табл. 4.2) и вычислив для них значения f’(x), f»(x).
Таблица 4.2
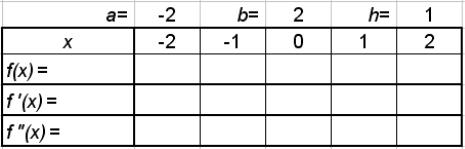
Задав шаг табулирования функции меньше, можно получить более точные интервалы отделения корней.
Функция f(x) меняет знаки на отрезках [-3, -2], [0, 1], [2, 3], следовательно, на этих отрезках отделены корни уравнения. На каждом из них отделено по одному корню уравнения, так как на отрезке [-3, -2] и f ‘(x), и f»(x) не меняют знак; на отрезке [0, 1 ] f ‘(x) не меняет знак; на отрезке [2, 3] и f ‘(x), и f»(x) не меняют знак.
Пример 4.2. Отделить все действительные корни уравнения
f(x) = x5 — 6x — 4 = 0
|
на отрезке [-2, 2]. |
||
|
Решение. |
||
|
f’(x) = |
, f»(x) = |
. |
Разделите отрезок [-2, 2] на четыре части, вычислите значения функции и производных на концах полученных отрезков и запишите полученные значения в таблице по форме 4.1.
Форма 4.1
Функция f(x) меняет знаки на отрезках [ , ], [ , ], [ , ], следовательно, на этих отрезках отделены корни уравнения. На каждом из них отделено по одному корню уравнения, так как ………………………………………………….
4.2. Методы уточнения корней
Уточнение корней – это доведение их до заданной степени точности. Существует несколько методов уточнения корней: метод половинного деления, метод хорд, метод касательных, комбинированный метод хорд и касательных, метод итераций. Мы рассмотрим уточнение корней методом касательных.
В дальнейшем будем считать, что функция f(x) непрерывна на промежутке [a, b], искомый корень х* отделен на этом промежутке и является единственным.
Метод касательных (Ньютона)
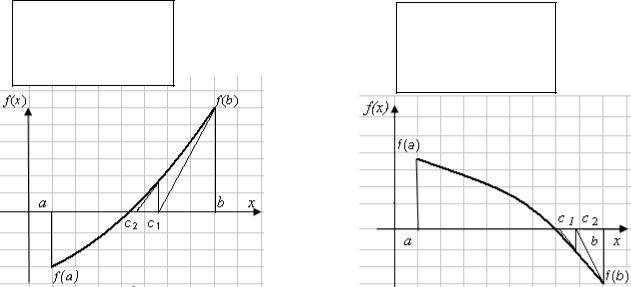
Суть метода заключается в том, что на промежутке [a, b] дуга кривой y = f(x) заменяется касательной к этой кривой. За приближенное значение корня принимается точка пересечения касательной с осью х (рис. 4.7, 4.8).Возможны следующие варианты:
Вариант 1. f(a) < 0, f(b) > 0, f’(x) > 0, f»(x) > 0, т.е. функция монотонновозрастающая, график функции – выпуклый вниз (рис. 4.7). Касательная к кривой в точке b пересекает ось х в точке с1, которая и принимается за первое приближение корня х1. Уравнение касательной к кривой в точке b есть
|
y f (b) |
||||
|
f (b) |
. |
(4.2) |
||
|
x b |
||||
Найдем значение x = x1, для которого y = 0.
|
x b |
f (b) |
. |
|
1 |
||
|
f (b) |
Эта формула носит название формулы метода касательных.
f(a) > 0, f(b) <
0,
f’(x) < 0 f‘‘(x)<
Теперь корень (первое приближение) находится внутри отрезка [a, c1]. Если значение корня не устраивает, его можно уточнить, применяя метод касательных к отрезку [a, c1]: построим касательную к кривой в точке с. Она пересекает ось х в точке с2. Точка пересечения касательной с осью х, принимается за второе приближение корня − х2.
|
x |
x |
f (x1) |
. |
|
|
2 |
1 |
|||
|
f (x1) |
||||
|
Продолжая этот процесс, находим |
|
x |
x |
f (xn ) |
. |
(4.3) |
||
|
n 1 |
n |
f |
||||
|
(xn ) |
Процесс уточнения продолжается до тех пор, пока не будет получен приближенный корень с заданной точностью ε, т.е. до тех пор, пока корень не будет отделен на отрезке [xn-1 — xn], для которого выполняется условие
|xn-1 — xn | < ε.
По формуле (4.2) корни вычисляются и для случая, когда f(a) > 0, f(b) < 0, f’(x) < 0, f»(x) < 0, т.е. функция монотонно-убывающая, а график функции – выпуклый вверх (рис. 4.8).
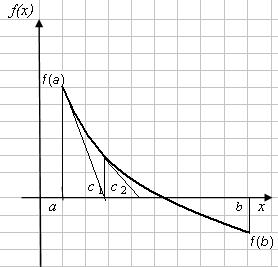
Вариант 2. f(a) > 0, f(b) < 0, f’(x) < 0, f»(x) > 0, т.е. функция монотонноубывающая, а график функции – выпуклый вниз (рис. 4.9).
Касательная к кривой в точке f(а) пересекает ось х в точке с1, которая принимается за первое приближение корня х1. Уравнение хорды есть
|
y f (a) |
||||||||
|
f |
(a) |
(4.4) |
||||||
|
x a |
||||||||
|
f(a) > 0, f(b) < |
||||||||
|
0, |
f(a) < 0, f(b) > |
|||||||
|
f’(x) < 0, f»(x) |
0, |
|||||||
|
f’(x) > 0 f»(x) < |
||||||||
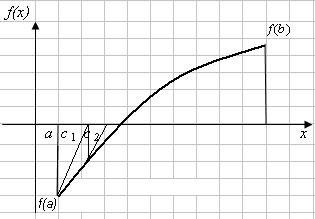
|
Рис. 4.9 |
Рис. 4.10 |
|
Найдем значение x = x1, для которого y = 0. |
|
x a |
f (a) |
, |
|
1 |
f |
|
|
(a) |
|
x |
x |
f (x1) |
, |
||||
|
2 |
1 |
f |
|||||
|
(x1) |
|||||||
|
или в общем виде |
f (xn ) |
||||||
|
x |
x |
(4.5). |
|||||
|
n 1 |
n |
f |
|||||
|
(xn ) |
Процесс уточнения продолжается до тех пор, пока не будет получено приближенное значение корня с заданной точностью ε.
По формуле (4.2) корни вычисляются и для случая, когда f(a) < 0, f(b) > 0, f’(x) > 0, f»(x) < 0, т.е. функция монотонно-возрастающая, график функции – выпуклый вверх (рис. 4.10).
На основании полученных выражений можно сформулировать правило: за исходную точку следует выбирать тот конец отрезка, для которого знак функции совпадает со знаком второй производной. В первом случае f(b)· f»(x) > 0, в качестве начального приближения берем точку b = x0 и используем формулу (4.3); во втором случае – f(a)· f»(x) > 0, в качестве начального приближения берем точку a = x0 и используем формулу (4.5).
Пример 4.1. (продолжение (см. стр. 47)). Уточнить корни уравнения f(x) = x3 —
8x + 2, отделенные на отрезках [-3, -2], [0, 1], [2, 3] методом касательных с точно-
стью ε = 0,005.
Решение.
1) Уточним корень уравнения f(x) = x3 -8x + 2, отделенный на отрезке [-3, -2]. f(a) = f(-3) = -1, f(b) = f(-2) = 10, f’(x) > 0, f»(x) < 0 (см. табл. 4.3 и рис. 4.11), по-

этому в качестве начального приближения возьмем точку a = -3 и используем для вычислений формулы (4.4) и (4.5), вспомогательные вычисления выполним в таблице (табл. 4.3).
Таблица 4.3
f ( 3) y f ( 3) . x ( 3)
|
x1 |
a |
f |
(a) |
3 |
1 |
2,947, |-2,947 – (-3)| = 0,053; |
||||
|
f |
19 |
|||||||||
|
(a) |
||||||||||
|
f (x ) |
0,025 |
0,053 > 0,005. |
||||||||
|
x2 |
x1 |
2,947 |
2,946, |
|||||||
|
1 |
|-2,946 – (-2,947)| = 0,001; |
|||||||||
|
f |
18,061 |
|||||||||
|
(x1 ) |
0,001 < 0,005,
следовательно, x = -2,946 − первый искомый корень уравнения f(x) = x3 -8x + 2, вычисленный методом касательных с точностью ε = 0,005.
2) Уточним корень уравнения f(x) = x3 -8x + 2, отделенный на отрезке [0, 1].
|
f(a) = f( ) = , f(b) = f( ) = |
, f’(x) 0, f»(x) 0, поэтому в качестве начального |
|
приближения возьмем точку |
и используем для вычислений формулы ( ) и |
( ), вспомогательные вычисления выполним в таблице по форме 4.2.
Форма 4.2

|
x |
x |
f (x1 ) |
|||
|
2 |
1 |
||||
|
f (x1 ) |
следовательно, x = – второй искомый корень уравнения f(x) = x3 -8x + 2, вычисленный с точностью ε = 0,005.
|
3) Уточним корень уравнения f(x) = x3 — 8x + |
2, отделенный на отрезке [2, 3]. |
|
|
f(a) = f( ) = , f(b) = f( ) = |
, f’(x) 0, f»(x) |
0, поэтому в качестве начального |
|
приближения возьмем точку |
= и используем для вычислений формулы (4.2) |
и (4.3), вспомогательные вычисления выполним в таблице по форме 4.3.
Форма 4.3
|
x |
b |
f (b) |
||||||||||||
|
1 |
||||||||||||||
|
f (b) |
||||||||||||||
|
x |
x |
f (x1 ) |
||||||||||||
|
2 |
1 |
|||||||||||||
|
f (x1 ) |
||||||||||||||
|
x3 |
x2 |
f (x |
2 |
) |
||||||||||
|
f (x2 ) |
||||||||||||||
|
Следовательно, x = |
– третий искомый корень уравнения f(x) = x3 — |
8x + 2, вычисленный с точностью ε = 0,005.
Метод половинного деления
Пусть на отрезке [a0, b0] имеется один корень. Разделим отрезок [a0, b0] пополам. Получим два отрезка [a0, с0] и [с0, b0], с0 = (a0 + b0)/2. За первое приближение корня х* принимается значение с0.
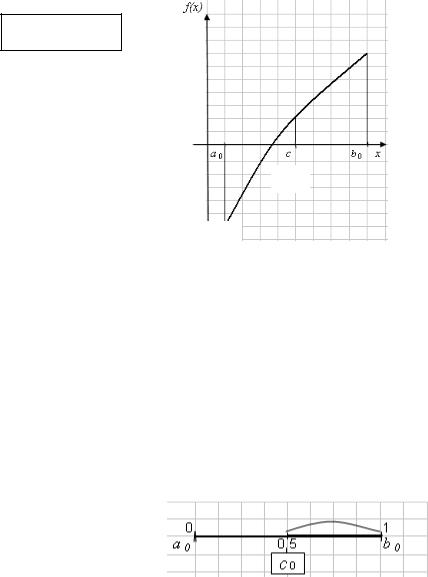
Для дальнейшего рассмотрения возьмем ту половину отрезка, где содержится корень, т.е. новый отрезок определяется соотношением:
|
[a1, b1 |
[a |
0 |
, c |
0 |
], |
если f (a |
0 |
) (c |
0 |
) 0, |
|
|
] |
], |
(4.6) |
|||||||||
|
[c0 |
, b0 |
если f (c0 ) (b0 ) 0. |
Процесс деления отрезков пополам продолжается до тех пор, пока длина очередного отрезка не станет меньше заданной точности ε. После выполнения n таких делений получим последовательность вложенных отрезков [a0, b0], [a1, b1], …, [an, bn], каждый из которых содержит корень х* в два раза меньше предыдущего.
f(a0)·f(c)
b
a Рис. 4.11
Пример 4.3. Уточнить корень уравнения x2 — 0,6 = 0, отделенный на отрезке
[0, 1] с точностью ε = 0,1.
Решение.
1) Вычислим значения функции f(х) = x2 — 0,6 на концах отрезка [0, 1]: f(0) = 0 – 0,6 = —0,6; f(1) = 1- 0,62 = 0,4.
Найдем середину отрезка: с0 = (a0 + b0)/2 = (0 + 1)/2 = 0,5. Поделим отрезок
[0, 1] пополам на два отрезка [0; 0,5] и [0,5; 1] (рис. 4.12).
Рис. 4.12
Вычислим значение функции при х = 0,5: f(0,5) = 0,52 — 0,6 = -0,35. Найдем произведение значений функции на концах каждого из полученных отрезков:

f(0)·f(0,5) = 0,21 > 0; f(0,5)·f(1) = -0,14 < 0.
Произведение значений функции меньше нуля на концах отрезка [0,5; 1], значит, на этом отрезке находится корень. Поэтому для дальнейшего рассмотрения возьмем отрезок [0,5; 1].
|1- 0,5| = 0,5 > ε =
Продолжим процесс вычислений.
2) Найдем середину отрезка: [0,5; 1]; с1 = (a1 + b1)/2 = (0,5 + 1)/2 = 0,75 (рис. 4.13).
Рис. 4.13
Вычислим значение функции при х = 0,75: f(0,75) = 0,752 — 0,6 = -0,038. Найдем произведение значений функции на концах каждого из полученных отрезков:
f(0,5)·f(0,75) = 0,013 > 0; f(0,75)·f(1) = -0,015 < 0.
Произведение значений функции меньше нуля на концах отрезка [0,75; 1], значит, на этом отрезке находится корень. Поэтому для дальнейшего рассмотрения возьмем отрезок [0,75; 1].
|1- 0,75| = 0,25 > ε =
Продолжим процесс вычислений.
3) Найдем середину отрезка: [0,75; 1]: с2 = (a2 + b2)/2 = (0,75 + 1)/2 = 0,875 (рис. 4.14). Вычислим значение функции при х = 0,875: f(0,875) = 0,166.
Рис. 4.14
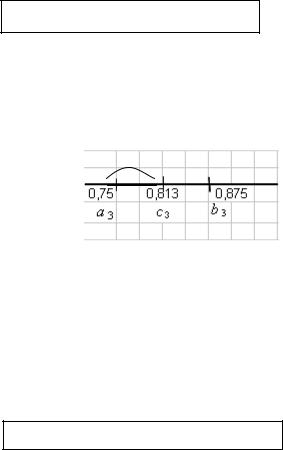
Найдем произведение значений функции на концах каждого из полученных отрезков:
f(0,75)·f(0,875) = -0,006 < 0; f(0,875)·f(1) = 0,066 > 0.
Произведение значений функции меньше нуля на концах отрезка [0,75; 0,875], значит, на этом отрезке находится корень. Поэтому для дальнейшего рассмотрения возьмем отрезок [0,75; 0,875].
|0,875 — 0,75| = 0,13 > ε =
Продолжим процесс вычислений.
4) Найдем середину отрезка: [0,75; 0,875]: с3 = (a3 + b3)/2 = (0,75 + 0,875)/2 = 0,813
(рис. 4.15). Вычислим значение функции при х = 0,813: f(0,813) = 0,06.
Рис. 4.15
Найдем произведение значений функции на концах каждого из полученных отрезков:
f(0,75)·f(0,813) = -0,002 < 0; f(0,813)·f(0,875) = 0,166 > 0.
Произведение значений функции меньше нуля на концах отрезка [0,75; 0,813], значит, на этом отрезке находится корень.
|0,813 — 0,75| = 0,06 < ε =
Поэтому процесс вычислений закончен. Приближенное значение корня x* = (0,75+0,813)/2 ≈ 0,78.
Вычисления удобно выполнять в таблице (табл. 4.4), а лучше в таблице Excel.
Таблица. 4.4
Окончание табл. 4.4
Пример 4.4. Уточнить корень уравнения x2 – 5x — 5 = 0, отделенный на отрез-
ке
[5, 7] с точностью ε = 0,1. Решение выполните самостоятельно в таблице по форме 4.4.
Форма 4.4
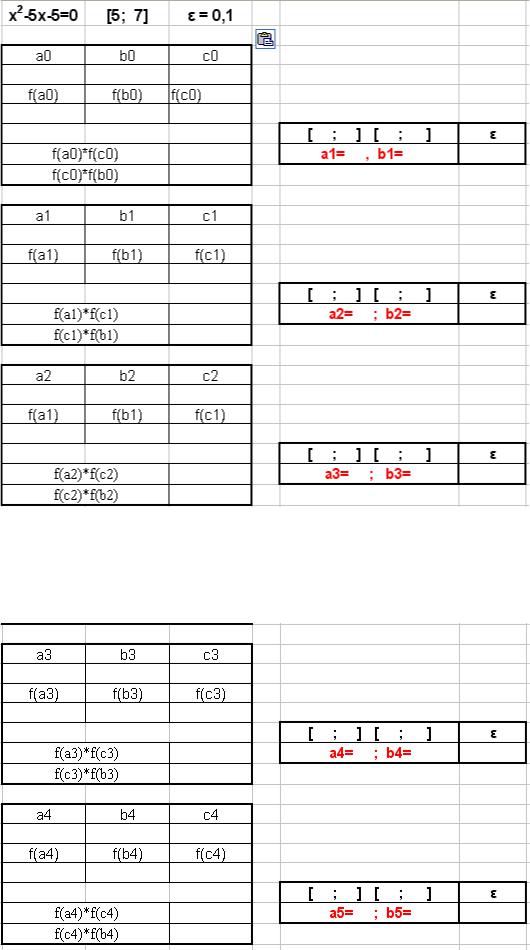
Окончание формы 4.4
Главная
»
Общенаучные дисциплины
»
Математика (2 семестр)
»
Приближенное вычисление действительных корней уравнения различными способами..
Приближенное вычисление действительных корней уравнения различными способами..
Содержание.
- Приближённое решение уравнений :
1.1 Способ хорд (или способ линейной интерполяции).
- Способ касательных (или способ Ньютона).
- Комбинированный способ (комбинированное применение способов хорд и касательных).
- Заключение.
- Список литературы.
Приближённое решение уравнений.
Если квадратные уравнения решали уже древние греки, то способы решения алгебраических уравнений третьей и четвёртой степени были открыты лишь в XVI веке. Эти классические способы дают точные значения корней и выражают их через коэффициенты уравнения при помощи радикалов различных степеней. Однако эти способы приводят к громоздким вычислениям и поэтому имеют малую практическую ценность.
В отношении алгебраических уравнений пятой и высших степеней доказано, что в общем случае их решения не выражаются через коэффициенты при помощи радикалов. Не выражаются в радикалах, например, корни уже такого простого по виду уравнения, как:
х^5-4х-2=0
Сказанное, однако, не означает отсутствия в науке методов решения уравнения высших степеней. Имеется много способов приближенного решения уравнений — алгебраических и неалгебраических (или, как их называют, трансцендентных), позволяющих вычислять их корни с любой, заранее заданной степенью точности, что для практических целей вполне достаточно.
На простейших из таких способов мы и остановимся, причём речь будет идти о вычислении действительных корней.
Пусть нужно решить уравнение:
f(x)=0 (1)
Если обратиться к рисунку, то каждый корень уравнения (1) представляет собой абсциссу точки пересечения графика функции y=f(х)
C осью Ох (рисунок №1)
С помощью графика функции или каким-нибудь иным способом обычно удаётся установить приблизительные значения корней. Это позволяет для каждого корня получить грубые приближения по недостатку и по избытку. Такого рода грубых приближений во многих случаях оказывается достаточно, чтобы, отправляясь от них, получить все значения корня с требуемой точностью. Об этом и пойдёт речь.
Итак, пусть корень Е уравнения (1) зажат между двумя его приближениями а и b по недостатку и по избытку а< E
Способ хорд (или способ линейной интерполяции).
Проведём хорду АВ (рисунок№3) и за первое приближённое значение корня примем абсциссу x1 точки С пересечения хорды с осью Ох.
Уравнение хорды имеет вид:
y-f(a)/f(b)-f(a)=x-a/b-a.
Поэтому в точке С:
-f(a)/f(b)-f(a)= x1-a/b-a
откуда:
x1=a- (b-a)*f(a)/ f(b)-f(a)
Рассмотрение всех четырёх случаев, изображённых на рисунке №2, показывает, что точка x1 лежит между a и b с той стороны от Е, где f(х) имеет знак, противоположный знаку f«(х).
Остановим внимание на первом случае: f`(х)>0, f«(х)>0 (рисунок №3), — в остальных случаях рассуждение вполне аналогично. В этом первом случае x1 лежит между a и Е. С отрезком [x1, b] поступаем так же, как мы поступаем с отрезком [a, b] (рисунок №4). При этом для нового приближённого значения корня получаем:
x1 = x2-(b- x1)*f(x1)/f(b)-f(x1)
( в формуле (2) заменяем x1 на x2, а на x1 ); значение x2 оказывается между x1 и Е. Рассматриваем отрезок [x2, b] и находим новое приближённое x3, заключённое между x2 и Е и. т. д. В результате получим последовательность а<x1<x2<x3<…<xn<…<E(3), всё более и более точных приближённых значений корня, причём хn+1 через xn выражается формулой:
хn+1= xn-(b- xn)*f(xn)/f(b)-f(xn) (4)
Для оценки погрешности соответсвующих приближений воспользуемся формулой Лагранжа:
f(xn)-f(E)=f`(c)*( xn-E) (xn<c<E)
или, поскольку
f(E)=0: f(xn)=f`(c)( xn-E),
откуда:
xn-Е= f(xn)/ f`(c)
Если обозначить через m наименьшее значение |f`(х)| на рассматриваемом отрезке, то для оценки погрешности получим формулу:
|xn-E|<|f`( xn)|/m (5)
Эта формула, заметим, совершенно не связана со способом отыскивания величин xn и, следовательно, приложила к приближённым значениям корня, получаемым любым методом. Формула (5) позволяет судить о близости xn к Е по величине значения f(xn). Однако в большинстве случаев она даёт слишком грубую оценку погрешности, т. е. фактическая ошибка оказывается значительно меньше.
Легко доказать, что последовательность приближений:
x1,x2,x3,…xn,… (6)
для корня Е, получаемых по способу хорд, всегда сходится к Е. Из случая, рассматривающегося выше, мы видим, что последовательность (6) — монотонная и ограниченная. Поэтому она имеет некоторый предел n
n=n-(b-n)f(n)/f(b)-f(n)
откуда F(n)=0. Так как f(x) возрастает на отрезке [a, b], то уравнение f(х)=0 имеет единственный корень, и этим корнем по условию является Е. Поэтому n=E, т. е. lim xn=E.
Пример № 1. Методом хорд найдём положительный корень уравнения
х^4-2х-4=0
с точностью до 0,01.
Решение:
Положительный корень будет находиться в промежудке (1; 1,7), так как f(1)=-5<0, а f(1,7)=0,952 >0
Найдём первое приближённое значение корня по формуле (2):
х1=1-91,7-1)* f(1)/ f(1,7)- f(1)=1,588;
так как f(1,588)=-0,817<0, то, применяя вторично способ хорд к промежутку (1,588; 1,7), найдём второе приближённое значение корня:
х2= 1,588-(1,7-1,588) f(1,588)/ f(1,7)- f(1,588)=1,639;
f(1,639)=-0,051<0.
Теперь найдём третье приближённое значение:
х3=1,639-(1,7-1,639) f(1,639)/ f(1,7)- f(1,639)=1,642;
f(1,642)=-0,016<0.
Теперь найдём четвёртое приближённое значение:
х4=1,642-(1,7-1,642) f(1,642)/ f(1,7)- f(1,642)=1,643;
f(1,643)=0,004>0
Следовательно, искомый корень с точностью до 0,01 равен 1,64.
1.2 Способ касательных (или способ Ньютона).
В том из концов дуги АВ (рисунок №5), в котором знаки f(х) и f«(х) совпадают, проводим касательную и за первое приближённое значение корня принимаем абсциссу х1` точки Д пересечения этой касательной с осью Ох. Обратимся вновь к первому случаю, соответствующему первому рисунку №2 (f`(x)>0, f«(x)>0), — в остальных случаях рассуждают опять-таки аналогично. Уравнение интересующей нас касательной имеет вид:
y-f(b)=f`(b)(x-b),
и поэтому в точке Д:
-f(b)=f`(b)(x1`-b),
откуда:
x1`=b-f(b)/f`(b).
Из рисунка видно, что x1` лежит между Е и b. С отрезком [a, x1`] поступаем так же, как с отрезком [a, b] ( рисунок №5), и в результате для нового приближённого значения корня получим:
х2` = x1`- f( x1`)/ f`( x1`).
Значение х2` оказывается между Е и x1`. Рассматриваем отрезок [a, х2`] и находим новое приближение х3` и т. д. В результате получим последовательность:
b> x1`> х2`> х3`>…>xn`>…>E (7)
все более точных приближённых значений корня, причём:
xn+1`= xn`- f(xn`)/ f`( xn`) (8)
Эта формула справедлива для всех четырёх случаев, изображённых на рисунке 32. Для оценки погрешностей полученных приближений можно опять воспользоваться формулой (5), как и в первом случае, легко устанавливается сходимость последовальности x1`, х2`, х3`,…,xn`,… к значению Е
Пример №2. Методом касательных найдём положительный корень уравнения
x^4-2x-4=0
с точностью до 0,01.
Решение:
В этом уравнении f(х)=х^4-2x-4, f`(х)=4х^3-2,а f«(х)=12x^2.Так как f(х) и f«(х) при х0 = 1,7 имеют один и тот же знак, а именно:
f(1,7)=0,952>0 и f«(1,7)>0, то применяем формулу:
x1`= х0- f(х0)/ f`( х0), где f`(1,7)=4*1,7^3-2=17,652. Тогда
x1=1,7- 0,952/17,652=1,646.
Применяем второй раз способ касательных:
х2= x1- f(x1)/ f` (x1), где f(x1)= f(1,646)=0,048, f` (1,646) =15,838;
x^2=1,646-0,048/15,838=1,643;
f(1,643)=0,004, f` (1,643)=15,740;
х3=1,643-0,004/15,740=1,6427.
Следовательно, искомый корень с точностью до 0,01 равен 1,64.
1.3 Комбинированный способ
(комбинированное применение способов хорд и касательных).
Этот способ состоит в одновременном использовании способов хорд и касательных. Остановим своё внимание опять на случае, отвечающем первому рисунку №2. Значения x1 и x1`, вычисляем по прежним формулам, т. е. принимаем:
x1=a-(b-a)f(a)/f(b)-f(a), (10)
x1`=b-f(b)/f`(b), причём: x1<E< x1`
Теперь вместо отрезка [a, b]рассматриваем отрезок [x1,x1`] (рисунок №6). Это даёт:
х2= x1-( x1`- x1)f(x1)/f(x1`)-f(x1),
х2`=x1`- f(x1)/f(x1`),причём х2<E< х2`
Далее рассматриваем отрезок [х2, х2`] и т. д.
В результате получаем:
хn<E< xn`,
хn+1= xn-( xn`- xn)f(xn)/f(xn`)-f(xn), а хn+1`= xn`-f(xn`)/f`( xn`) (11)
В данном случае мы приближаемся к корню сразу с обеих сторон (рисунок №6), а не с одной стороны, как в способе хорд и способе касательных. Поэтому разность xn`- xn позволяет судить о качестве полученных приближений, и никакие формулы для оценки здесь не нужны.
Пример№3. Комбинированным способом способом вычислим с точностью до 0,0005 положительные корни уравнения
X^5-x-0,2=0
Решение: График многочлена f(x)= X^5-x-0,2 для х>0 изображён на рисунке №7. Из этого рисунка видно, что уравнение имеет положительный единственный корень, лежащий на отрезке 1<x<1,1. Поскольку f`(x)=5x^4-1, f«(x)=20x^3, постольку на интересующем нас отрезке f`(x0>0,f«(x)>0 т. е. знак производных сохраняется. Применяем комбинированный способ:
f(a)=f(1)=-0,2, f(b)=f(1,1)=0,31051, f`(b)=f`(1,1)=6,3205.
Формулы (10) дают:
x1=1+0,1*0,2/0,51051=1,039,
x1`=1,1-0,31051/6,3205=1,051
При этом x1`- x1=0,012, т. е. точность недостаточна. Совершаем второй шаг:
f(1,039)=-0,0282;f(1,051)=0,0313,f`(1,051)=5,1005.
По формулам(11):
х2=1,039=0,012*0,0282/0,0595=1,04469,х2`=1,051-0,0313/5,1005=1,04487.
При этом х2`- х2=0,00018, т. е. точность достаточна. Таким образом:
1,04469 <E< 1,04487
Любое из фигурирующих здесь чисел можно взять за приближённое значение Е, причём ошибка не превзойдёт 0,00018.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.
Пусть имеется уравнение вида
f(x)= 0
где f(x) — заданная алгебраическая или трансцендентная функция.
Решить уравнение — значит найти все его корни, то есть те значения x, которые обращают уравнение в тождество.
Если уравнение достаточно сложно, то задача точного определения корней является в некоторых случаях нерешаемой. Поэтому ставится задача найти такое приближенное значение корня xПP, которое отличается от точного значения корня x* на величину, по модулю не превышающую указанной точности (малой положительной величины) ε, то есть
│x* – xпр │< ε
Величину ε также называют допустимой ошибкой, которую можно задать по своему усмотрению.
Этапы приближенного решения нелинейных уравнений
Приближенное решение уравнения состоит из двух этапов:
- Отделение корней, то есть нахождение интервалов из области определения функции f(x), в каждом из которых содержится только один корень уравнения f(x)=0.
- Уточнение корней до заданной точности.
Отделение корней
Отделение корней можно проводить графически и аналитически.
Для того чтобы графически отделить корни уравнения, необходимо построить график функции f(x). Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения.
Для примера рассмотрим задачу решения уравнения
где угол x задан в градусах. Указанное уравнение можно переписать в виде
Для графического отсечения корней достаточно построить график функции
Из рисунка видно, что корень уравнения лежит в промежутке x∈(6;8).
Аналитическое отделение корней
Аналитическое отделение корней основано на следующих теоремах.
Теорема 1. Если непрерывная функция f(x) принимает на концах отрезка [a; b] значения разных знаков, т.е.
то на этом отрезке содержится по крайней мере один корень уравнения.
Теорема 2. Если непрерывная на отрезке [a; b] функция f(x) принимает на концах отрезка значения разных знаков, а производная f'(x) сохраняет знак внутри указанного отрезка, то внутри отрезка существует единственный корень уравнения f(x) = 0.
Уточнение корней
Для уточнения корней может использоваться один из следующих методов:
- Метод последовательных приближений (метод итераций)
- Метод Ньютона (метод касательных)
- Метод секущих (метод хорд)
- Метод половинного деления (метод дихотомии)
Метод последовательных приближений (метод итераций)
Метод итерации — численный метод решения математических задач, используемый для приближённого решения алгебраических уравнений и систем. Суть метода заключается в нахождении по приближённому значению величины следующего приближения (являющегося более точным). Метод позволяет получить решение с заданной точностью в виде предела последовательности итераций. Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения решения.
Функциональное уравнение может быть записано в виде
Функцию f(x) называют сжимающим отображением.
Последовательность чисел x0, x1 ,…, xn называется итерационной, если для любого номера n>0 элемент xn выражается через элемент xn-1 по рекуррентной формуле
а в качестве x0 взято любое число из области задания функции f(x).
Реализация на C++ для рассмотренного выше примера
Уравнение может быть записано в форме
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x, double eps)
{
double rez; int iter = 0;
cout << «x0= » << x << » «;
do {
rez = x;
x = 1 / (sin(M_PI*x / 180));
iter++;
} while (fabs(rez — x) > eps && iter<20000);
cout << iter << » iterations» << endl;
return x;
}
int main()
{
cout << find(7, 0.00001);
cin.get();
return 0;
}
Результат выполнения

Метод Ньютона (метод касательных)
Если известно начальное приближение x0 корня уравнения f(x)=0, то последовательные приближения находят по формуле
Графическая интерпретация метода касательных имеет вид
Реализация на C++
Для заданного уравнения
производная будет иметь вид 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x, double eps)
{
double f, df; int iter = 0;
cout << «x0= » << x << » «;
do {
f = sin(M_PI*x / 180) — 1 / x;
df = M_PI / 180 * cos(M_PI*x / 180) + 1 / (x*x);
x = x — f / df;
iter++;
} while (fabs(f) > eps && iter<20000);
cout << iter << » iterations» << endl;
return x;
}
int main()
{
cout << find(1, 0.00001);
cin.get(); return 0;
}
Результат выполнения

Метод секущих (метод хорд)
Если x0, x1 — приближенные значения корня уравнения f(x) = 0 и выполняется условие
то последующие приближения находят по формуле
Методом хорд называют также метод, при котором один из концов отрезка закреплен, т.е. вычисление приближения корня уравнения f(x) = 0 производят по формулам:
Геометрическая интерпретация метода хорд:
Реализация на C++
В отличие от двух рассмотренных выше методов, метод хорд предполагает наличие двух начальных приближений, представляющих собой концы отрезка, внутри которого располагается искомый корень.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x0, double x1, double eps)
{
double rez = x1, f0, f;
int iter = 0;
cout << «x0= » << x0 << » x1= » << x1 << » «;
do {
f = sin(M_PI*rez / 180) — 1 / rez;
f0 = sin(M_PI*x0 / 180) — 1 / x0;
rez = rez — f / (f — f0)*(rez — x0);
iter++;
} while (fabs(f) > eps && iter<20000);
cout << iter << » iterations» << endl;
return rez;
}
int main()
{
cout << find(1.0, 10.0, 0.000001);
cin.get(); return 0;
}
Результат выполнения

Метод половинного деления (метод дихотомии)
Если x0, x1 — приближенные значения корня уравнения f(x) = 0 и выполняется условие
то последующие приближения находятся по формуле
и вычисляется f(xi). Если f(xi)=0, то корень найден. В противном случае из отрезков выбирается тот, на концах которого f(x) принимает значения разных знаков, и проделывается аналогичная операция. Процесс продолжается до получения требуемой точности.
Геометрическая интерпретация метода дихотомии
Реализация на C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double func(double x)
{
return (sin(M_PI*x / 180) — 1 / x);
}
double find(double x0, double x1, double eps)
{
double left = x0, right = x1, x, fl, fr, f;
int iter = 0;
cout << «x0= » << x0 << » x1= » << x1 << » «;
do {
x = (left + right) / 2;
f = func(x);
if (f > 0) right = x;
else left = x;
iter++;
} while (fabs(f) > eps && iter<20000);
cout << iter << » iterations» << endl;
return x;
}
int main()
{
cout << find(1.0, 10.0, 0.000001);
cin.get(); return 0;
}
Результат выполнения
Для численного поиска решения также можно использовать генетические алгоритмы.
Назад: Алгоритмизация

















