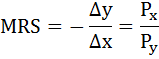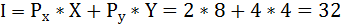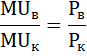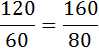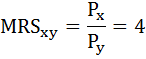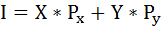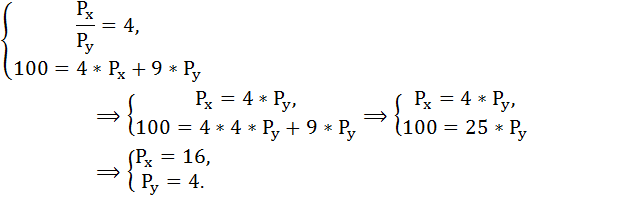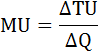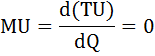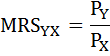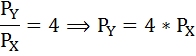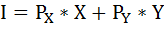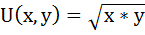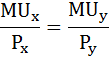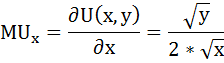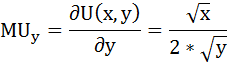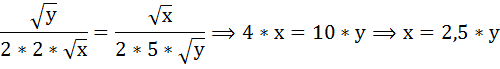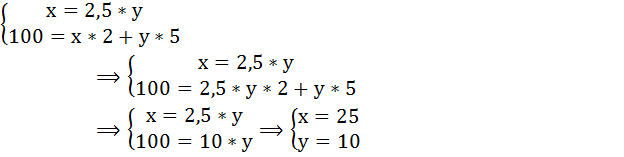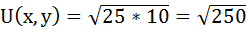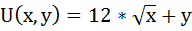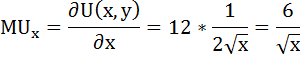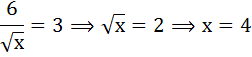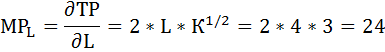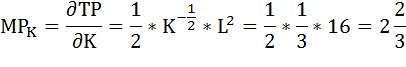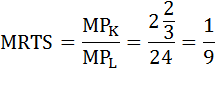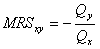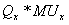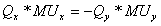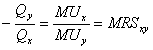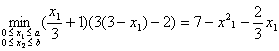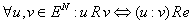Задача № 1 Расчёт дохода потребителя
Индивид покупает 8 единиц товара Х и 4 единицы товара Y. Найти его доход, если известно, что цена товара Х равна 2 ден. ед., а предельная норма замены равна 0,5.
Решение:
В точке оптимума выполняется равенство:
По условию MRS = 0,5 и Рх = 2. Следовательно, Ру = Рх / MRS = 2/0,5=4.
Найдём доход индивида, используя бюджетное ограничение:
где I – доход,
Рх и Ру – цены двух рассматриваемых благ,
Х и Y – их количества.
Задача № 2. Расчёт общей и предельной полезности
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара — Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) — TU(1)=30 – 19 = 11
MU(3)= TU(3) — TU(2)=38 – 30 = 8
MU(4)= TU(4) — TU(3)=43 – 38=5
MU(5)= TU(5) — TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) — TU(2)=39 – 32=7
MU(4)= TU(4) — TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:
Задача № 3. Расчёт общей полезности
Предельная полезность первой единицы блага равна 420. При потреблении первых трёх единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 4 раза. Найти общую полезность блага при условии, что его потребление составляет 8 единиц.
Решение:
Распишем условие задачи следующим образом:
MU(1) = 420,
MU(2) = 420/2=210,
MU(3) = 210/2=105,
MU(4) = 105/4=26,25,
MU(5) = 26,25/4=6,5625,
MU(6) = 6,5625/4=1,640625,
MU(7) = 1,640625/4=0,410156,
MU(8) = 0,410156/4=0,102539.
Найдём общую полезность блага при условии, что его потребление составляет 8 единиц.
TU(8) = MU(8) + TU(7) = MU(8) + MU(7) + TU(6) =…=
= MU(8) + MU(7) + MU(6) + MU(5) + MU(4) + MU(3) + MU(2) + MU(1) =
= 420 + 210 + 105 + 26,25 + 6,5625 + 1,640625 + 0,410156 + 0,102539 = 769,96582
Задача № 4. Расчёт оптимального объёма потребления двух благ
В таблице представлены следующие данные о предельной полезности двух благ.
| Количество, кг | Конфеты | Виноград |
|---|---|---|
| 1 | 60 | 150 |
| 2 | 40 | 120 |
| 3 | 20 | 90 |
Цена 1 кг конфет 80 ден. ед., а цена 1 кг винограда 160 ден. ед.
Бюджет потребителя составляет 400 ден. ед.
Определить оптимальный объём потребления конфет и винограда.
Решение:
Оптимальный объём потребления конфет и винограда достигается тогда, когда отношение предельных полезностей равно отношению цен этих благ.
Среди перечисленных вариантов таким свойством обладает комбинация 2 кг винограда (MUв=120) и 1 кг конфет (MUк=60).
Предельная полезность винограда, разделённая на предельную полезность конфет равна отношению их цен:
Проверим соответствие этой комбинации бюджетному ограничению:
80*1 + 160*2 = 400
Бюджет полностью израсходован.
Задача № 5. Расчёт цен товаров Х и Y
Потребитель покупает 4 единицы блага Х и 9 единиц блага Y, имея доход 100 ден. ед. Найти цены товаров X и Y, если известно, что предельная норма замены товара Y товаром X (MRSxy) равна 4.
Решение:
Предельную норму замены товара Y товаром X(MRSxy) можно определить как отношение цены товара Х к цене товара Y:
Запишем бюджетное ограничение:
100 = 4*Px + 9*Py,
где
Px, Py – цены благ Х и Y соответственно.
Составим и решим систему уравнений:
Задача № 6. Расчёт оптимального объёма потребления
У студента Иванова в холодильнике сыр и колбаса нарезаны для удобства кусочками по 100 г. Общая полезность их потребления представлена в таблице. Определите количество съеденного им в день, если известно, что он в целом употребляет 700 г названных продуктов и при этом добивается максимума полезности.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) |
| 100 | 2000 | 1900 |
| 200 | 3900 | 3750 |
| 300 | 5700 | 5550 |
| 400 | 7400 | 7300 |
| 500 | 8000 | 9000 |
| 600 | 9500 | 10650 |
Решение:
Рассчитаем предельную полезность от потребления этих двух продуктов.
Предельная полезность в дискретном случае определяется по формуле:
где
ΔTU – приращение общей полезности (TU1 – TU0),
ΔQ – приращение количества потребляемого блага (Q1 – Q0).
Вычисления занесём в таблицу.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) | Предельная полезность колбасы | Предельная полезность сыра |
| 100 | 2000 | 1900 | 2000 | 1900 |
| 200 | 3900 | 3750 | 1900 | 1850 |
| 300 | 5700 | 5550 | 1800 | 1800 |
| 400 | 7400 | 7300 | 1700 | 1750 |
| 500 | 9000 | 9000 | 1600 | 1700 |
| 600 | 10500 | 10650 | 1500 | 1650 |
Известно, что в целом студент употребляет 700 г колбасы и сыра, то есть всего 7 кусочков, и при этом добивается максимума полезности.
Решение об оптимальном объёме потребления можно представить в виде таблицы, где на каждом шаге будем сравнивать предельную полезность каждого кусочка колбасы и сыра и выбирать наибольшую величину предельной полезности, что в сумме даст их максимум.
Итак, на первом шаге наибольшая предельная полезность, равная 2000 будет получена от потребления 1 кусочка/100 грамм колбасы. Дальше студенту без разницы, что употребить, так как первый кусочек сыра и второй кусочек колбасы приносят одинаковую полезность – 1900. Пусть, например, это будет сначала сыр, а затем колбаса. Но вот на четвёртом шаге наибольшую полезность принесёт второй кусочек сыра. Предельная полезность, полученная от его потребления 1850 больше, чем 1800 – предельная полезность третьего куска колбасы или третьего кусочка сыра. На пятом шаге студенту опять всё равно, что съесть первым, третий кусочек сыра или третий кусочек колбасы, так как полезность от дополнительного потребления этих продуктов одинакова. И наконец, седьмым кусочком должен стать сыр, поскольку предельная полезность четвёртого кусочка сыра (1750), больше чем предельная полезность четвёртого кусочка колбасы (1700).
Общая полезность от потребления 3 кусочков колбасы и 4 кусочков сыра будет максимальной и составит:
TU = 2000 + 1900 + 1900 + 1850 + 1800 + 1800 + 1750 = 13 000
Таким образом, студент Иванов получит максимум полезности при употреблении 3 кусочков (300 грамм) колбасы и 4 кусочков (400 грамм) сыра.
Задача № 7. Расчёт отимального объёма потребления
Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:
1) U(Q)= 1 – 5 × Q2
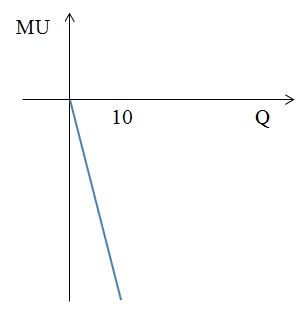
2) U(Q)= 5 + Q – Q2
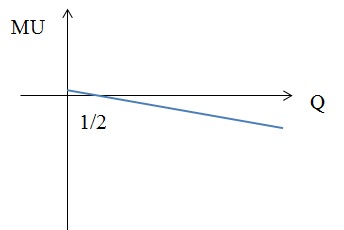
3) U(Q) = Q2 – 5 × Q3
Как будут выглядеть функции предельной полезности? Проиллюстрируйте ответ.
Решение:
Оптимальный для потребителя объем блага Q будет определяться в точке, где потребитель получит максимум удовлетворения полезности. Задача сводится к нахождению экстремума функции полезности. Найдём производную функции полезности (предельную полезность MU) и приравняем её к нулю.
1) MU = –10 × Q = 0, следовательно, Q = 0;
2) MU = 1 – 2 × Q = 0, следовательно, Q = 1/2;
3) MU = 2 × Q – 15 × Q2 = 0, следовательно, Q = 0; Q = 2/15.
Задача № 8. Расчёт цен товаров X и Y
Индивид покупает 4 единицы блага X и 9 единиц блага Y, имея доход равный 100 денежным единицам. Найти цены товаров X и Y, если известно, что предельная норма замены X на Y равна 4.
Решение:
По условию задачи предельная норма замены благом Y блага X () равно 4. Это значит, что количество блага Х должно быть сокращено на 4 единицы в обмен на увеличение количества блага Y на единицу, при неизменном уровне удовлетворения потребителя.
Равновесие потребителя может быть представлено математически как:
— это предельная норма замещения, равная отношению цен благ Y и X. Данное условие оптимума потребителя следует понимать так. Соотношение, в котором потребитель при данных ценах способен замещать один товар другим, равно соотношению, в котором потребитель согласен замещать один товар другим, не изменяя уровень своего удовлетворения.
Отсюда
Далее воспользуемся формулой бюджетного ограничения:
где I – доход или бюджет потребителя.
100 = 4 × PX + 9 × PY
100 = 4 × PX + 9 × 4 × PX
100 = 40 × PX
PX = 2,5
PY = 4 × 2,5 = 10.
Ответ: PX = 2,5; PY = 10.
Задача № 9. Определение рационального выбора потребителя
Потребитель имеет функцию полезности:
и может на свой доход равный 100 единицам приобретать только эти два товара по ценам:
Px = 2
Py = 5
Определить рациональный выбор потребителя. Какой максимальный уровень полезности достижим?
Решение:
Рациональный выбор потребителя осуществляется в соответствии со вторым законом Госсена:
Предельная полезность товара х будет равна производной функции общей полезности по аргументу х:
Аналогично находим предельную полезность товара y:
Далее воспользуемся бюджетным ограничением:
Из условия задачи известно, что:
I = 100
Px = 2
Py = 5
Составим и решим систему уравнений:
При х = 25 и у = 10 общая полезность достигнет максимума:
Задача № 10. Расчёт оптимального объёма потребления
У Оксаны есть 30 рублей. Она хочет купить шоколадки «Шок» ценой 3 р. Полезность от этой покупки она оценивает функцией:
х – приобретённое количество шоколадок,
y – оставшаяся часть дохода.
Сколько купит шоколадок «Шок» рациональная Оксана?
Решение:
Рациональное поведение потребителя можно определить, как стремление максимизировать излишек потребителя. Потребитель будет покупать дополнительные единицы до тех пор, пока они приносят дополнительный избыток, т.е. пока цена, которую потребитель готов уплатить за единицу блага, превосходит реальную цену:
MU > P
Однако каждая последующая единица потребления обычно приносит уменьшающийся прирост полезности, т.е. при покупке благ «одно за другим» рано или поздно предельная полезность какого-то блага сравняется с его ценой:
MU = P
После того как предельная полезность сравняется с ценой, потребитель прекратит дальнейшие покупки: оптимальный объём потребления достигнут.
Найдём предельную полезность MU, как производную функции общей полезности по аргументу х:
Оптимальный объём потребления будет достигнут при МU = P:
Таким образом, рациональная Оксана купит 4 шоколадки, потратив на эту покупку 12 рублей.
Технология производства фирмы описывается производственной функцией
Q = L2 ×K ½.
Определите предельный продукт труда, предельный продукт капитала и норму технологического замещения капитала трудом, если
K = 9, L = 4.
Решение:
Предельный продукт труда определяется, как производная функции общего продукта по аргументу L:
Предельный продукт капитала определяется также через производную функции общего продукта, но по аргументу К:
Предельная норма технического замещения характеризует норму, по которой предприятие может замещать в производстве один ресурс другим.
Найдём предельную норму технологического замещения капитала трудом:
Одной единицей труда может быть замещено 1/9 единицы капитала.
Задача
1
Полезность
равна 2x2
+ 3y2.
Найдите предельную норму замещения
продукта х в наборе (3,4).
Решение.
Предельная
норма замены товара х товаром у
— это
количество товара х, которое потребитель
согласен потерять с тем, чтобы получить
дополнительную единицу товара y
и оказаться на том же уровне полезности:
MRS
= – Δ
Qx / Δ
Qy
или
MRS
= MUx / MUy ,
где:
MUx
–
предельная полезность товара х;
MUy
–
предельная полезность товара y.
Находим
MUx
и MUy
как частные производные функции
полезности по переменным x
и y
соответственно:
1)
MUx = d
(2x2
+ 3y2)
/ dx
= 4x,
2)
MUy = d
(2x2
+ 3y2)
/ dy
= 6y.
Находим
предельную норму замещения продукта х
в наборе (3,4):
MRS
= 4x
/ 6y
= 4*3/6*4 = 0,5.
Ответ:
Предельная
норма замещения товара х в наборе (3,4)
равна 0,5.
Задача
2
Функция
спроса первого потребителя имеет вид:
Q1
=
6 – Зр, функция спроса второго –
Q2
=
4 –
0,5р. Построить кривую суммарного спроса.
Решение:
Общий
спрос на товары (услуги) определяется
поведением каждого покупателя на рынке
данного товара (услуги). Для каждого
покупателя можно построить индивидуальную
кривую спроса. Суммарный спрос будет
представлять при этом общий спрос
потребителей. Кривую рыночного спроса
получают в результате сложения по
горизонтали кривых индивидуального
спроса, просуммировав абсциссы кривых
при каждом значении цены.
1)
Находим максимальную цену спроса для
первого потребителя:
Q1
=
6 – Зр, 6 – Зр = 0, p
= 2.
2)
Находим максимальную цену спроса для
второго потребителя:
Q2
=
4 – 0,5р, 4 – 0,5р = 0, p
= 8.
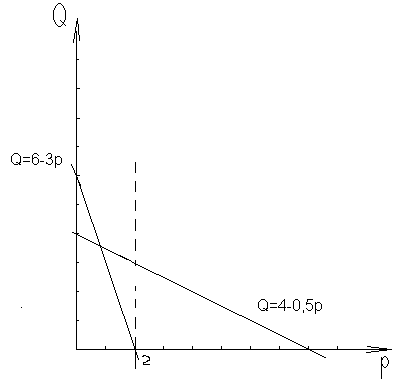
Поэтому
при ценах, меньших 2, суммарный спрос
равен Q
= Q1+
Q2,
или
Q
= 10 –
3,5p;
2)
При ценах, больших 2, суммарный спрос
равен спросу второго потребителя;
3)
Суммарный спрос при цене 2 равен 10 –
3,5p
= 10 –
3,5*2
= 3.
Ответ:
График
суммарного спроса представляет собой
ломанную АВС, где А (10; 0), В (3;2) и С(0;8).
Задача
3
Производственная
функция имеет вид: p
= L0.8
* K0.2.
Издержки производителя равны 30. Цена
труда 4. Цена капитала 5. Найти равновесный
расход ресурсов.
Решение:
Эффективность
производства достигается тогда, когда
ресурсы распределяются таким образом,
чтобы обеспечить максимально возможный
чистый выигрыш от их применения.
Правило
минимизации издержек производителя в
долгосрочном периоде выглядит следующим
образом:
MPL
/ PL
= MPK
/ PK
, где
MPL
– предельный продукт по труду,
MPк
– предельный продукт по капиталу,
PL–
цена труда,
PK
–
цена капитала.
Находим
MPL
и
MPK,
как частные производные производственной
функции по переменным L
и K
соответственно:
MPL
=
dP
/ dL
= 0,8K0.2/
L-0.2
MPK
=
dP
/ dK
= 0,2L0.8/
K-0.8
Тогда:
(0,8K0.2
/ L-0.2)
/4 = (0,2L0.8
/ K-0.8)
/5
После
преобразований и вычислений получаем:
L=5K.
Из
условия известно, что издержки
производителя равны 30:
K+L=30.
Тогда:
K+5K
=30, K=5,
L=25.
Ответ:
Равновесный расход ресурсов — затраты
труда равны 25, затраты капитала равны
5.
Задача
4
Издержки
конкурентной фирмы равны: TC
= 20 + 33Q
– 4Q2
+ Q3,
где Q
– выпуск. При каких ценах продукта
целесообразно продолжить производство?
Найдите цену предложения фирмы при
выпуске 3.
Решение.
1)
Совокупные издержки фирмы (ТС) складываются
из фиксированных (TFC)
и переменных (TVC):
TC=TFC+TVC.
В
нашем случае:
TFC=20,
TVC=33Q
– 4Q2
+ Q3.
Определяем
средние переменные издержки:
AVC
= TVC
/Q
= 33 – 4Q
+ Q2.
В
краткосрочном периоде конкурентной
фирме целесообразно продолжать
производство при условии, что цена
продукта Р больше средних переменных
издержек:
P
> AVC.
В
условиях совершенной конкуренции
максимизация прибыли фирмы достигается
при условии:
P
= MC,
где
MC
– предельные издержки.
Находим
предельные издержки фирмы:
MC
= dTVC
/ dQ
= d(33Q
– 4Q2
+ Q3)
/ dQ,
MC
= 33 – 8Q + 3Q2.
Условие,
когда производство нецелесообразно:
цена продукта Р равна средним переменным
издержкам:
P
= AVC,
так
как P=MC,
то:
33
– 8Q + 3Q2
=
33 – 4Q + Q2,
2Q2
= 4Q,
Q
= 2.
Следовательно,
P
= 33 – 8*2 + 3*22
=
29.
2)
В условиях совершенной конкуренции
предложение фирмы в краткосрочном
периоде определяется ее предельными
издержками, то есть:
S
= MC.
Для
Q
= 3 имеем:
S
= MC
= 33 – 8Q
+ 3Q2
= 33 – 8*3 + 3*32
=
36.
Ответ:
Производство
целесообразно продолжать при ценах
больше 29.
Цена
предложения при объеме производства 3
равна 36.
Задача
5
фирма
прибыль неоклассический концепция
В
городе одна Пиццерия. Спрос на пиццу Q
= 100 –
2p.
Каждый дополнительный рабочий увеличивает
выпуск на 4 пиццы в час. Нанято 6 рабочих.
Найдите предельную доходность 6-го
рабочего.
Решение:
1)
Шесть рабочих за час выпустят 6*4=24 пиццы.
Находим цену спроса пиццы:
Выразим
р через Q:
р
= 50 –
0,5Q,
р
= 50 –
0,5*24,
р
= 38.
2)
Находим общий доход.
Валовой
доход равен
цене товара, умноженной на количество
проданных единиц:
TR
= P*Q,
TR
= 38*24 = 912.
3)
Находим
предельный доход.
Предельный
доход
—
это
дополнительный доход, полученный от
производства одной дополнительной
единицы продукции:
МR
= ΔTR
/ ΔQ,
MR
= (TR)’ = (Q*(50 –
0,5Q))’
= 50 –
Q
= 50 –
24
= 26.
4)
Предельный продукт одного рабочего:
MPf
=
4.
Находим
предельный доход от предельного продукта
6-го рабочего:
MRPf
=
MPf
* MR
= 4*26 = 104.
Ответ:
Предельная
доходность 6-го рабочего равна 104.
Заключение
Фирма
— хозяйственная единица, обладающая
обособленным
имуществом и оформленными правами,
позволяющими ей осуществлять хозяйственную
деятельность под свою имущественную
ответственность. Одной из самых главных
целей фирмы является стремление к
максимизации прибыли.
Фирма
максимизирует
прибыль в случае равенства предельной
выручки и предельных издержек:
МR
=
МС
=>
II
= mах.
Итак,
принцип
максимизации прибыли говорит
о том, что в целях достижения максимальной
прибыли фирма должна выбрать такой
объем выпуска, при котором значения
предельной выручки и предельных издержек
равны.
Прибыль
— превышение в денежном выражении
доходов (выручки от реализации товаров
и услуг) над затратами на производство
или приобретение и сбыт этих товаров и
услуг.
Основные
функции прибыли следующие:
1.
Оценочная функция. Прибыль является
показателем, который наиболее полно
отражает эффективность производства
и оценивает хозяйственную деятельность
предприятия.
2.
Стимулирующая функция. Прибыль
способствует повышению эффективности
финансово-хозяйственной деятельности
предприятия.
3.
Прибыль — источник формирования бюджетных
ресурсов и внебюджетных фондов.
В
практике употребляются следующие
понятия прибыли: валовая (балансовая)
прибыль, прибыль от реализации основных
фондов и иного имущества предприятия,
прибыль по внереализационным операциям,
чистая прибыль.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Но в какой мере может потребитель отказаться, например, от апельсинов, чтобы приобрести дополнительно еще одно яблоко? Это помогает определить т.н. предельная норма замещения.
Предельная норма замещения Y на Х (МRSху) – количество товара Y, от которого потребитель отказался бы, чтобы получить еще одну единицу товара X, при этом оставаясь на данной кривой безразличия. Кривизна изображенных ранее кривых безразличия означает, что количество Y, от которого потребитель хочет отказаться ради еще одной единицы X, уменьшается по мере увеличения количества X, замещающего Y в наборе.
Чтобы увидеть это начнем двигаться вдоль кривой безразличия, изображенной на рис. 6.4. Qу – недельное потребление товара Y, от которого потребитель отказался бы, чтобы получить еще одну единицу товара X. Выигрыш в недельном потреблении единицы товара Х составляет Qх = 1.
Количество товара Y, которое будет обменено на единицу товара X, между любыми двумя точками на кривой может быть записано как Qу/Qх. Это наклон кривой безразличия, вдоль которой движется потребитель, отказываясь от единиц товара Y, для получения единиц товара X. Однако наклон кривых безразличия отрицателен.
Такое рассмотрение MRSху приводит к получению отрицательного числа. Предельная же норма замещения определяется как положительное количество товара Y, от которого потребитель желает отказаться ради дополнительной единицы X. Поэтому он есть произведение наклона кривых безразличия на -1.
Кривизна кривой безразличия, изображенная на рис. 6.4. подразумевает уменьшение предельной нормы замещения Y на X. Обратите внимание, как их наклон изменяется по мере того, как потребитель, следуя по данной кривой, замещает Y на X. По мере того, как Х замещает Y вдоль кривой, она становится менее крутой.
Рис. 6.4 – Уменьшение MRSху вдоль кривой безразличия
Таблица 6.2 – Предельная норма замещения Y на X
| Набор | Qу | Qх | MRSху |
|
М1 М2 М3 М4 |
10 6 3 1 |
4 5 6 7 |
4 ед. Y за 1 ед. Х 3 ед. Y за 1 ед. Х 2 ед. Y за 1 ед. Х |
Анализ кривых безразличия не требует, чтобы полезность была количественно измерима, достаточно только предположить, что потребители способны ранжировать альтернативы, то есть, что полезность порядково измерима (позиция ординалистов).
Если бы полезность была количественно измерима (позиция кардиналистов), была бы возможность вычислить, сколько полезности при добавлении в набор еще одной единицы товара или услуги. То есть предельную норму замещения вдоль кривой безразличия можно связать с предельными полезностями благ на каждой из осей.
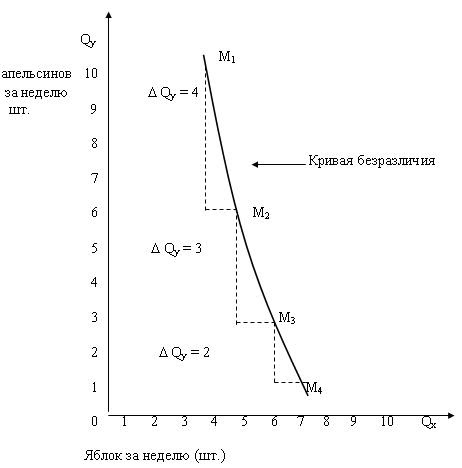
Изъятие Qу единиц товара Y из набора наносит потребителю ущерб. Потеря полезности составляет Qу MUу, где МUу – предельная полезность Y для потребителя. При замене потерянного количества Y тем количеством X, которое необходимо для возвращения потребителя в состояние прежней удовлетворенности, приобретенная полезность составила бы
(где МUх – предельная полезность X). Если потребителю необходимо вернуться на ту же самую кривую безразличия, прирост полезности от добавления Х равен потери полезности от изъятия Y. Таким образом:
Следовательно,
Предельная норма замещения Y на Х поэтому может рассматриваться как отношение предельной полезности Х к предельной полезности Y.
В нашем примере предельная полезность яблок (товар Х) уменьшается, когда его количество растет, и, соответственно она увеличивается у апельсинов (товар Y), когда их количество уменьшается. Поскольку МUх уменьшается, когда товар Х (яблоки) замещает товар Y (апельсины), в то время как МUу увеличивается, отношение МUх/МUу равное МRSху уменьшается.
Отсюда вытекает, что предельная норма замещения Y на Х тоже должна падать при замене Y на X, если предельные полезности Х и Y находятся в обратном отношении к количествам этих товаров, покупаемых за период.
Уменьшение предельной полезности товаров, при предположении количественной измеримости полезности, объяснило бы выпуклую форму кривых безразличия.
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете заказать решение задач, написание учебных работ и онлайн помощь
Подробнее
Общая полезность
Общая полезность — удовлетворение, которое получают от потребления определенного набора товара или услуги.
Предельная полезность — это прирост общей полезности товарного набора при увеличении объема потребления данного товара на единицу.
Mu = (Tu1 — Tu0)/(Q1 — Q0)
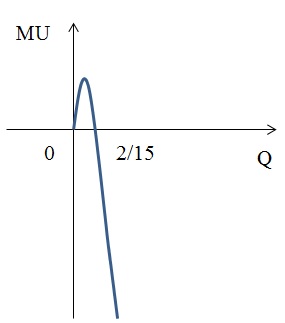
Производная по количеству Q
Mu = dTu/dQ
Как найти производную.
Например, TU = x*y. Mux = d(x*y)/dx = y; Muy = d(x*y)/dy = x
Например, TU = 10x2 + 2x + 2. Mux = d(10x2 + 2x + 2)/dx = 20x + 2
Функция полезности — функция, показывающая убывание полезности блага с ростом его количества:
Tu = f(Qi)
Условия равновесия потребителя
Условия равновесия потребителя можно выразить формулой:Mux / Muy = Px / Pyгде Px и Py — цены на товары X и Y.
Точка касания кривой безразличия с бюджетной линией означает равновесие потребителя.
Пример задачи на нахождение оптимального набора покупок
Пример задачи на нахождение оптимального набора товаров при заданной функции полезности
Кривая безразличия
Кривая безразличия — это множество точек на кривой, которые показывают различные комбинации двух экономических благ, имеющих одинаковую полезность для потребителя.
Предельная норма замещения (marginal rate of substitution — MRS) — количество, на которое потребление одного из двух благ должно быть увеличено (или уменьшено), чтобы полностью компенсировать потребителю уменьшение (или увеличение) потребления другого блага на одну дополнительную единицу:
MRSxy = ΔY / ΔXΔY = Y1 — Y0ΔX = X1 — X0илиMRSxy = Mux / Muy
Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.
Бюджетная линия
Бюджетная линия представляет собой прямую линию с отрицательным наклоном, графически отображающую множество наборов из двух товаров, требующих одинаковых затрат на их потребление. Она показывает, какие потребительские наборы можно приобрести за данную сумму денег.I = PxX + PyYгде I — доход потребителя;
Px — цена блага Х;
Py — цена блага Y;
X,Y — составляют соответственно купленные количества благ.
Пример. Функция полезности U(xy)=xy. Доход потребителя равен 80 ден. ед. Цены товаров x и y соответственно равны Px=2 руб. и Py=4 руб. Найдите равновесный набор.
Решение: Из условия равновесия потребителя: Mux / Muy = Px / Py получаем: Mux = d(x*y)/dx = y; Muy = d(x*y)/dy = x
Тогда: y / x = 2 / 4 = 1/2 или y = 1/2x
Для наших данных уравнение бюджетной линии запишем как: 80 = 2x + 4y = 2x + 4*1/2x = 4x
Откуда: x = 20 ед., y = 1/2*20 = 10 ед.
Ответ: потребитель приобретет 20 ед. товара x и 10 ед. товара y.
Пример решения определения оптимума потребителя
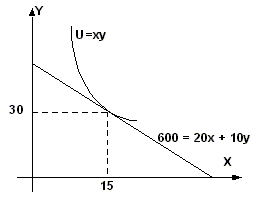
Потребитель тратит 600 рублей в месяц на приобретение двух товаров. Цена товара Х — 20 рублей, а товара Y — 10 рублей. Задана функция полезности потребителя U = ХY. Составить уравнение бюджетной линии. Найти предельную норму замещения. Определить оптимум потребителя. Представить графически. Если цена товара Х уменьшится на 5 руб., на сколько единиц изменится объем спроса данного товара всего?|Уравнение бюджетной линии:I = PxX + PyY 600 = 20X + 10Y
Предельная полезность товаров:
Mux = dU/dx = d(xy)/dx = yMuy = dU/dy = d(xy)/dy = x
Оптимум потребителя достигается при равенстве:
Mux / Muy = Px / PyMux / Muy = 20 / 10 = 2
Предельная норма замещения
MRSxy = Mux / Muy = 2
Выразим y через x.
Mux / Muy = y / x = 2y = 2x
Подставим в уравнение бюджетной линии:
600 = 20x + 10*2x = 20x + 20xоткуда X = 15; Y = 2x = 30
Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.
Проверка: 20 х 15 + 10 х 30 = 300 + 300 = 600.
При уменьшении цены товара X на 5 руб.
Px = 20 — 5 = 15
Найдем новый оптимум потребителя.
600 = 15X + 10Y = 15X + 20X = 35Xоткуда x = 17.14; y = 2x = 34.29
Спрос на товар Х увеличился на 2.14 (17.14 — 15)
Проверка: 15 х 17.14 + 10 х 34.29 = 257.1 + 342.9 = 600.
Пример нахождения цен товаров при оптимальном выборе покупателя
Утилитарное решение и решение, оптимальное по Нэшу
Определить утилитарное решение и решение, оптимальное по Нэшу, если функции полезности агентов равны u1 = х1 + 3, u2= 3х2 — 2 при х1 + x2 = 3 . Проверить независимость от масштаба для указанных ПКБ, если функция полезности первого агента была уменьшена в три раза.
Решение. Определим эгалитарное решение, для этого должно выполняться условие u1 = u2 или x1 + 3 = 3x2 — 2. Учитывая, что x2 = 3- x1, получаем x2 = 2, тогда x1 = 1. Вектор полезностей (4,4).
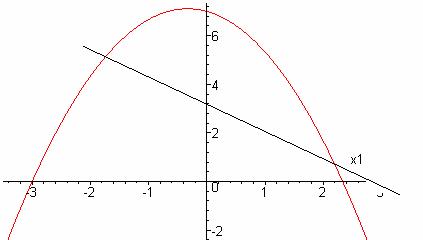
Утилитарное решение находим, максимизируя сумму полезностей агентов: x1 + 3 + 3x2 — 2 → max, подставив x1 вместо x2, получаем 4x2 + 1 → max. Рассматриваемая функция возрастает от x1 и достигает своего максимума при x1 = 3, тогда x2 = 0. Здесь вектор полезностей (1,1).
Независимость от масштаба
Определим эгалитарное решение, для этого должно выполняться условие u1 = u2 или x1/3 + 1 = 3x2 — 2. Учитывая, что x2 = 3- x1, получаем 10/3 x1 — 6 = 0, тогда x1 = 9/5, то x2 = 6/5. Вектор полезностей (8/5,8/5).
Множество допустимых распределений пары продуктов на неотрицательные количества определяется так:x1,x2 0, x1 + x1 = a, x2 = b.
Максимизируя ФКП Нэша, мы выбираем эффективное распределение. Оптимальное распределение определяется как решение задачи:
Минимум достигается x1 = 2,17; x2 = 0,83.
Видим, что соблюдается условия:
а) 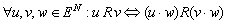
б)