Как найти предел измерения формула

Содержание:

При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с  точностью до сантиметра, размеры дома, стадиона – с точностью до метра.

Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.

При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.

Пример:

Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).

Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением 
шкалы линейки совпадает второй край стола  (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)

Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.  

Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.

Относительная погрешность измерения ε (ЭПСИЛОН)

Иногда важно знать, какую часть составляет наша погрешность от значения 
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: .  То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой  (эпсилон): 

     (5.1)

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения –  плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.

Стандартная запись результата измерений и выводы

Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 0,5) мм — Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.

На точность измерения влияет много факторов, в частности:

1. При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
2. Не вполне ровно установили рулетку.
3. Наша рулетка является копией эталона и может несколько отличаться от оригинала.

Все это необходимо учитывать при проведении измерений.

Итоги:

• Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
• Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора. 
• Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:   и указывает на качество измерения. Ее можно выразить в процентах.

Измерительные приборы

Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.

Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.

Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.

Как определяют единицы длины и времени

В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.

Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).

Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.

Можно ли расстояние измерять годами

Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!

Что надо знать об измерительных приборах

Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?

Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.

Как определить цену деления шкалы? Для этого необходимо:

1. выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
2. подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
3. вычесть из большего значения меньшее (4 см — 3 см = 1 см) и результат разделить на число делений.

Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.

Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2: 

А какими линейкой и мензуркой можно измерить точнее?

Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.

Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше  Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы ), мензуркой 2 — с точностью до 1 мл (сравните с ценой деления ). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.

Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.

Главные выводы:

1. Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
2. Цена деления шкалы равна значению наименьшего деления шкалы.
3. Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.

Для любознательных:

В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.

• Заказать решение задач по физике

Пример решения задачи

Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:

1) Цена деления нижней шкалы:

Цена деления средней шкалы: 

Цена деления верхней шкалы:

2) Определенный но нижней шкале с точностью до 10° определенный по средней шкале с точностью до 5° определенный по верхней шкале с точностью до 1°

При
работе на стендах в электротехнической
лаборатории наряду с обычными 
электроизмерительными приборами часто
используется комбинированный
электроизмерительный комплект 
К-540.

Измерительный
комплект К-540 рассчитан на работу в
трёхфазных и однофазных цепях и содержит
три  измерительных прибора:

—
два прибора с независимыми переключаемыми
пределами измерений :

вольтметр
(15
– 600 В)
и амперметр
(0,1
– 50 А), 

—
третий прибор – ваттметр,
предел измерений которого зависит от
выбранных пределов измерений вольтметра
и амперметра.

Предел измерений ваттметра определяется

как
произведение выбранных пределов
вольтметра и амперметра.

Поскольку
относительная погрешность измерений
снижается к концу шкалы прибора,

то
с целью повышения точности измерений
номинальные значения

 (пределы
измерений) вольтметра  U
_ном
[B]
 и
амперметра 
I
_ном
 [A]

 выбирают
как
ближайшее большее значение 
к измеряемым (заданным) значениям

напряжения 
 U
_и
[B] 
и
тока  
I
_и
 [A]
.

Установка
выбранных пределов на приборах комплекта
выполняется путём переключения клавиш
вольтметра или перестановки штекера
амперметра в гнездо, соответствующее
выбранному пределу измерения.

После
установки пределов измерений вольтметра 
U
_ном
 
и  амперметра 
I
_ном
 предел 
измерений ваттметра комплекта К-540 
определяется как произведение выбранных
пределов измерений по напряжению и по
току :

   P
_ном
w
 = 
U_ном* I
_ном
 [Bт].

Если
в процессе выполнения работы изменяют
предел измерений вольтметра или
амперметра комплекта, то одновременно
следует  определить новый предел
измерений ваттметра.

 Цена
деления шкалы каждого из приборов
комплекта определяется как отношение
установленного предела измерений
(номинального значения) соответствующего
прибора 
А
_ном  к
числу делений всей шкалы прибора N [дел]:

 С
 _{(V,
A
, W)} 
=  А
_{ном (V,
A
, W)}
 /
N  
[B,
A,
Bт
/ дел].

Показание
прибора в делениях шкалы  n
[дел]
по заданной величине (напряжение, ток
или мощность) можно определить путём
деления заданной величины  А
_и 
на
цену деления шкалы соответствующего
прибора :  

n
_{(V,
A
, W)} 
= 
 А
_{и
(V,
A
, W)}
 /
С
_{(V,
A
, W)}
 [дел].

Измеряемую
электрическую величину А
_и
(напряжение, ток или мощность) по
показаниям прибора можно определить
путём умножения цены деления шкалы
прибора  С
_{(V,
A
, W)} 

на
число делений шкалы
n [дел],
указываемых стрелкой прибора:  

 А
_{и
(V,
A , W)}  =
 С
_{(V,
A , W)}
*
n 
 [B,
A, Bт]
.

Если
при проведении измерений показания
вольтметра или амперметра комплекта
находятся в начальной части шкалы, то
для снижения погрешности измерений
необходимо:

1. Переключить предел измерения данного прибора на ближайшее меньшее значение.

2.
Заново определить цену деления этого
прибора, а также предел измерения и цену
деления ваттметра.

 Если
при проведении измерений произошло или
возможно «зашкаливание» вольтметра
или амперметра комплекта, то во избежание
порчи прибора необходимо:

1.
Переключить предел измерения данного
прибора на ближайшее большее значение.

2.
Заново определить цену деления этого
прибора, а также предел измерения и цену
деления ваттметра.

В
начало страницы

5.
ОСОБЕННОСТИ ПОДКЛЮЧЕНИЯ ИЗМЕРИТЕЛЬНОГО
КОМПЛЕКТА К-540

Для
наглядного сравнения условно-графического
обозначения комплекта и его контурного
изображения  ниже приведены
электрическая и монтажная схемы
включения  измерительного комплекта
в электрическую цепь (рис. 1).

Рис.
1. Электрические принципиальная и
монтажная схемы

включения 
комплекта К-540 в электрическую цепь

Для
работы в однофазных цепях обычно
используются пара входных (A
— n)
и пара выходных (A
— n)
клемм комплекта.  Входные клеммы
комплекта  (A
— n)
с помощью монтажных проводов подключаются
к гнёздам питающей сети  (~
0 – 220 В
), расположенных на горизонтальной
панели стенда. На этой же панели находится
ручка регулятора напряжения (РНО —
регулятор напряжения однофазный или
ЛАТР — лабораторный автотрансформатор),
вращением которой можно регулировать
подаваемое напряжение  от нуля до
250
В.

Выходные
клеммы комплекта (A
— n) 
с помощью монтажных проводов соединяются
по схеме, заданной в лабораторной работе,
с элементами блока нагрузки расположенного
на лицевой панели стенда и содержащего
резисторы, конденсаторы, индуктивность,
лампочку накаливания, стендовые
измерительные приборы, коммутационные
устройства и др.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #

  19.04.2015382.32 Кб516.pdf

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Протокол исследований с учетом знаний о метрологии

Термины и определения в метрологии

Как и любая другая наука, метрология имеет свой собственный язык – это термины и определения. Эти понятия используются дальше при знакомстве с нормативными документами и оценках результатов измерений или их сравнений. И нам необходимы эти знания, чтобы научиться правильно работать с нормативными документами, извлекая из них требуемую информацию.

В нормативном документе – рекомендациям по межгосударственной стандартизации «РМГ 29-2013 ГСИ Метрология. Основные термины и определения» дано пояснение и толкование 231 метрологическому понятию. Конечно, для наших целей такой список слишком велик. Наша цель – выделить тот их необходимый минимум, который позволит нам на практике правильно воспринимать и оценивать результаты измерений.

Рассмотрим пока всего только 9 самых важных понятий:

Метрология — Наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
Комментарий: мы должны привлечь аппарат этой науки для целей объективной оценки качества измерений в измерительных лабораториях.

Результат измерения (РИ) – Множество значений величины, приписываемых измеряемой величине вместе с любой другой доступной и существенной информацией.
Комментарий: значения измеряемых показателей, которые мы видим, например, в протоколах испытаний/

Метрологические характеристики:

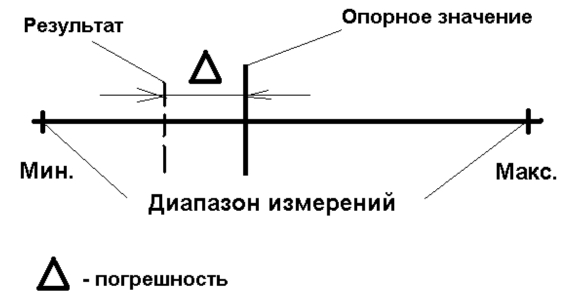
Погрешность РИ – Разность между измеренным значением величины и опорным значением величины.
Комментарий:на примере пакета с мукой: мы видим опорное значение (2 кг), а погрешность (разность с опорным значением) может достигать или 40 г, или 2% в зависимости от формы представления погрешности (см. ниже).

Абсолютная погрешность РИ – Погрешность измерения, выраженная в единицах измеряемой величины.
Комментарий: на примере пакета с мукой: абсолютная погрешность может составлять 40 г.

Относительная погрешность РИ – Погрешность измерения, выраженная отношением абсолютной погрешности измерения к опорному значению измеряемой величины.
Комментарий: на примере пакета с мукой: относительная погрешность прямо указана на его этикетке – 2%.

Границы абсолютной (относительной) погрешности: — Верхняя и нижняя границы интервала, внутри которого с заданной вероятностью находится значение погрешности измерений.
Комментарий: на примере пакета с мукой: видим на этикетке пакета границу относительной погрешности +/-2% или на этикетке может быть также указано +/-40 г в виде границы абсолютной погрешности.

Диапазон измерений – Множество значений величин одного рода, которые могут быть измерены данным средством измерений или измерительной системой с указанными инструментальной неопределенностью или указанными показателями точности при определенных условиях.
Комментарий: на примере пакета с мукой: например, весы для взвешивания пакетов с мукой могут обеспечивать указанную погрешность только в пределах от 100 г и до 10 кг (исходя из технических характеристик технических весов). Это и есть их рабочий диапазон измерений.

Повторяемость измерений (сходимость) – Прецизионность (точность) измерений в условиях повторяемости измерений (Один из наборов условий измерений, включающий применение одной и той же методики измерений, того же средства измерений, участие тех же операторов, те же рабочие условия, то же местоположение и выполнение повторных измерений на одном и том же или подобных объектах в течение короткого промежутка времени).
Комментарий: на примере лабораторных испытаний:допускаемый разброс результатов определений, по одной и той же пробе у одного и того же оператора, работающего на одной и той же измерительной установке в режиме непрерывных определений параметров пробы в одной и той же лаборатории.

Воспроизводимость измерений (прецизионность): — Прецизионность (точность) измерений в условиях воспроизводимости измерений (Один из наборов условий измерений, включающий разные местоположения, разные средства измерений, участие разных операторов и выполнение повторных измерений на одном и том же или аналогичных объектах).
Комментарий: на примере протокола лабораторных испытаний из 2-х или более лабораторий: допускаемый разброс результатов измерений, выполненных по одной и той же пробе в разных лабораториях у разных операторов, работающих на разных измерительных установках по одной и той же методике измерений.

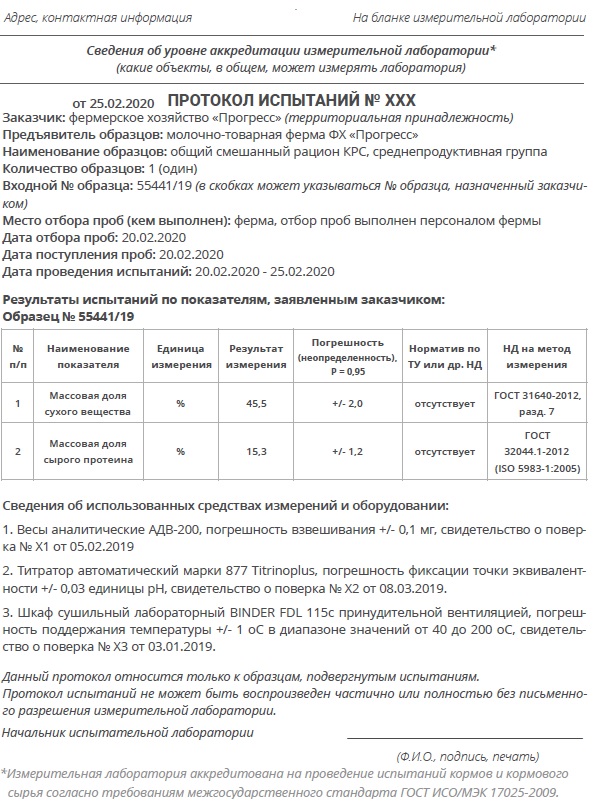
Более наглядно указанные метрологические характеристики можно увидеть на нижеприведенных иллюстрациях, но перед этим снова обратимся к уже знакомому нам Протоколу испытаний:

Рассмотрим в качестве примера более подробно метрологические характеристики метода определения содержания сухого вещества (далее по тексту – СВ) в общем смешанном рационе (далее по тексту – ОСР). В протоколе имеется ссылка на соответствующий нормативный документ — ГОСТ 31640-2012 Корма. Методы определения содержания сухого вещества (можно найти в Интернете в свободном доступе).

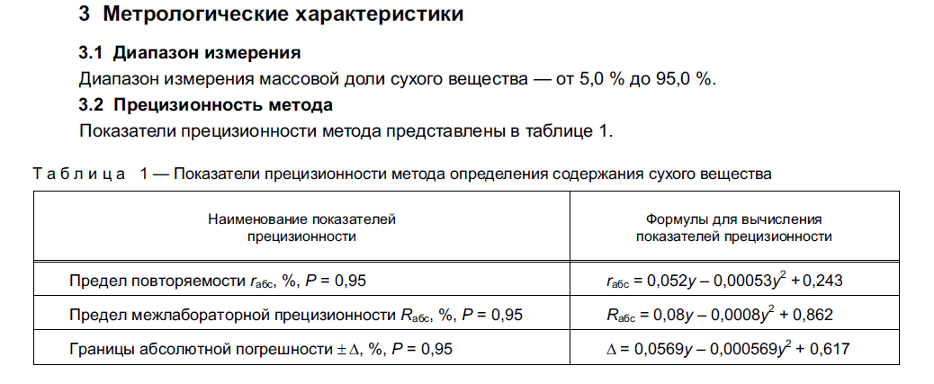
В разделе 3, Таблица 1 документа помещены метрологические характеристики этого метода:

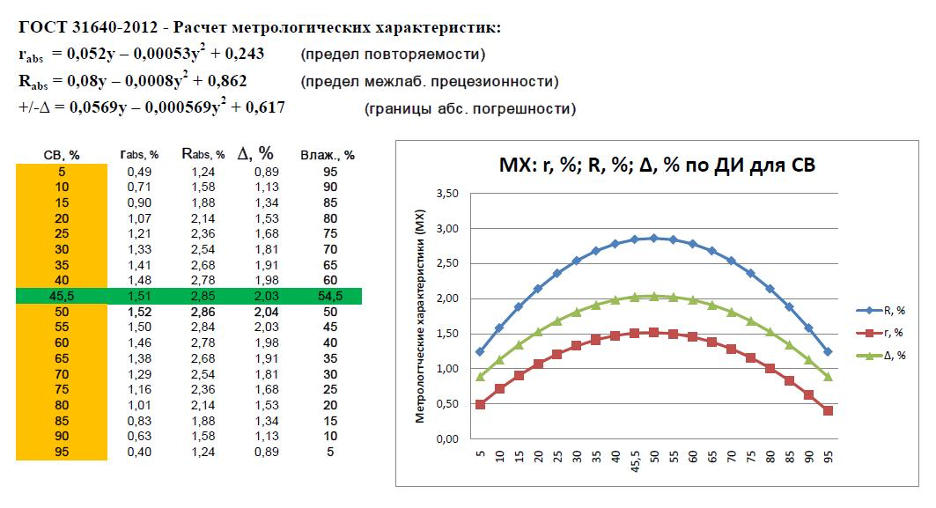
Используя формулы, приведенные в Таблице 1, и данные из Протокола по содержанию СВ в ОСР (y = 45,5%), можно выполнить расчет и оценить метрологические характеристики метода в его рабочем диапазоне измерений от 5% до 95% массовой доли СВ:

Итак, мы теперь можем разобрать 4 наиболее важные характеристики любого метода измерений: диапазон измерений, повторяемость, воспроизводимость и погрешность. В метрологии их принято представлять пределами или границами (см. пояснения по тексту ниже).

Диапазон измерений

Характеристика средства измерений (прибора) или методики выполнения измерений, описывающая допускаемый интервал значений для результатов измерений, простирающийся от минимального до максимального возможного значения измеряемой величины.

Так рабочий диапазон измерения этой линейки от 0 см и до 20 см. То же справедливо и для методик физико-химического анализа – каждая из них имеет свой диапазон измерений.

Что это означает на практике?

Например, в случае методики выполнения измерений содержания СВ в кормах по ГОСТ 31640-2012 диапазон измерения составляет от 5% и до 95%.

Зачем нужно его знать?

Это нужно для понимания: к каким именно образцам применим этот метод измерения. Для образцов содержанием СВ выше 95% или ниже 5% указанный метод применять нельзя, в этом случае надо искать другой метод, который обеспечивает измерения в более широком диапазоне содержания СВ.

Ответственность за выбор подходящего метода лежит на лаборатории, хотя заказчик, исходя из своих задач и требований, может также самостоятельно делать выбор конкретного метода измерения.

Сходимость (повторяемость) результатов измерений

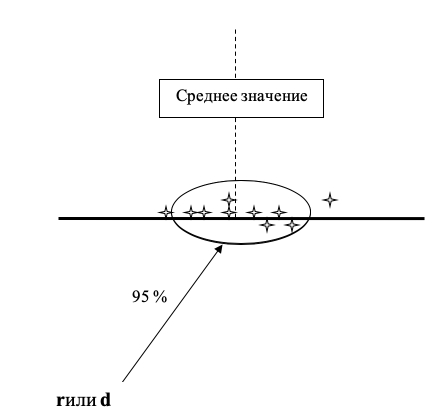
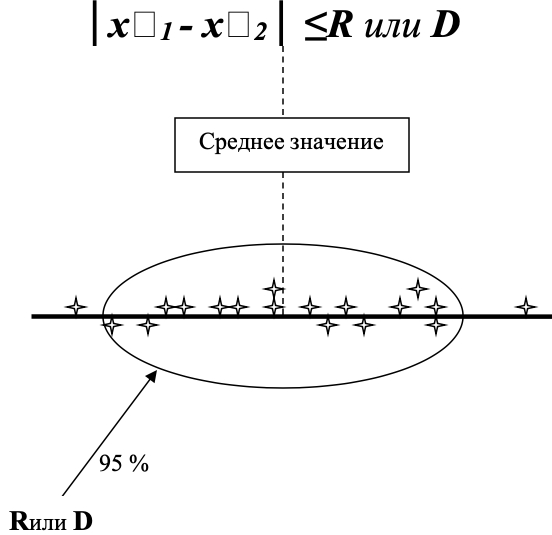
Качество измерений, отражающее близость друг к другу результатов измерений (x1 и x2), выполненных в одинаковых условиях. Оценивается через предел сходимости (d) или предел повторяемости (r):

│x1 — x2│ ≤r или d

Предел сходимости (повторяемости) характеризует разброс единичных измерений, например, у одного оператора при выполнении измерений в серии при стабильных условиях.

При этом 95% единичных измерений укладывается в предел повторяемости.

Для наглядности снова обратимся ГОСТ 31640-2012. В Таблице 1 приводится формула для расчета предела повторяемости (r_abs, %, P = 0,95).

Как расшифровать эту запись? Она означает, что предел повторяемости по этой формуле будет выражен в абсолютных процентах от измеренного значения содержания СВ, а доверительная вероятность (P) при этом составляет 0,95. В пояснениях к Таблице 1 в ГОСТ 31640-2012 по этому поводу сказано следующее: «Расхождение результатов двух параллельных определений, полученными в условиях повторяемости, может превышать предел повторяемости r не более одного раза из двадцати». Последнее означает, что 95% указанных расхождений укладывается в данный предел.

Теперь снова обратимся к Протоколу. Результат измерения содержания СВ в нем представлен значением 45,5%. Выполним расчет по формуле для предела повторяемости (r_abs), задавая значение содержание СВ из Протокола вместо (y) в формуле и по требованию ГОСТ 31640-2012, проведя округление результата вычислений до первого десятичного знака. Полученное значение предела повторяемости составит 1,5% абсолютных.

Что это означает на практике?

Например, если оператор в лаборатории выполнил 2 параллельных определения СВ для одного и того же образца ОСР, а результаты этих определений были: 44,8 и 46,2%, и разница результатов определений составляет т.о. 1,4%, то оператор может выполнить вычисление среднего значения определений, которое будет 45,5% и будет представлено в итоговом Протоколе в качестве результата измерения, т.к. норматив оперативного контроля результатов измерений у оператора (r_abs = 1,5%) не был превышен.

Однако, если бы результаты определений были бы другими: 44,3% и 46,7%, а разница в этом случае составила бы 2,4%, имело бы место значительное превышение предела повторяемости, равного 1,5%, хотя среднее значение было бы тем же – 45,5%!

В этом случае оператор НЕ ИМЕЕТ ПРАВА вычислять среднее и представлять его как результат измерений. Оператор должен снова повторить 2 определения, вычислить разницу и проверить: не превышен ли норматив оперативного контроля 1,5 %. Если не превышен, вычислить результат измерения как среднее из 2-х определений – 45,5%, или, в противном случае, все измерения прекращаются до выяснения причин превышения предела: неисправное оборудование, испорченные реактивы, не соблюдение стабильных условий при выполнении определений и т.д.

Воспроизводимость результатов измерений

• измерений, отражающее близость друг к другу результатов измерений (x1 и x2), выполненных в различных условиях (в различное время, в различных местах, разными методами и средствами). При выполнении измерений в различных лабораториях оценивается предел межлабораторной воспроизводимости (D) или межлабораторной прецизионности (R).

Предел воспроизводимости (межлабораторной прецизионности) характеризует разброс результатов измерений, например, у разных операторов при выполнении измерений в различных условиях или разброс результатов измерений одного и того же объекта в различных лабораториях.

При этом 95% результатов измерений укладывается в предел воспроизводимости (прецизионности).

Понятно, что R или D для одного и того же объекта измерения и метода всегда больше r или d.

Совершенно аналогично на основании формулы из Таблицы 1 и измеренного содержания СВ, указанного в Протоколе (у = 45,5%) можно оценить предел воспроизводимости (R), который в данном случае составит 2,9% (после округления).

Что это означает на практике?

Если один и тот же материал образца был отправлен на анализ в ДВЕ различные лаборатории, выполняющие измерения ОДНИМ и ТЕМ ЖЕ методом, но на разных комплектах оборудования, разными операторами и т.д., то мы получим два Протокола.

Рассмотрим теперь эти два Протокола из 2-х лабораторий. Пусть в первом был представлен результат измерения содержания СВ на уровне 45,5%, а во втором – 47,9%, соответственно.

Разность РИ составляет 2,4% и НЕ ПРЕВЫШАЕТ предел воспроизводимости (R = 2,9%), который рассчитан для среднего из 2-х РИ 46,7%. В таком случае наиболее достоверным будет среднее из 2-х РИ, т.е. 46,7%. Именно его надо использовать в дальнейшем как окончательный РИ.

Однако в случае, если в первом Протоколе было представлен результат измерения содержания СВ в ОСР, например, 42,3%, а во втором Протоколе – 45,5%. Разность РИ будет достигать 3,2%.

Как в таком случае оценить такие результаты: приемлемы ли они?

Если разность между РИ в условиях воспроизводимости составляет 3,2%, это ПРЕВЫШАЕТ предел воспроизводимости (R = 2,9%) — значит такие результаты не могут рассматриваться как удовлетворяющие условию воспроизводимости РИ и достоверные.

Как определить какой результат ближе к истинному?

Это требует привлечения метрологических знаний, выходящих за рамки предмета данной статьи. Но сделать это возможно с помощью специальных процедур контроля точности лабораторных измерений, описываемых, в частности в международном стандарте ГОСТ ИСО/МЭК 17025-2009 ОБЩИЕ ТРЕБОВАНИЯ К КОМПЕТЕНТНОСТИ ИСПЫТАТЕЛЬНЫХ И КАЛИБРОВОЧНЫХ ЛАБОРАТОРИЙ ISO/IEC 17025:2005.

Погрешность результата измерений

Погрешность выглядит как отклонение (в любую возможную сторону) результата измерений от опорного значения:

Но, поскольку отклонения результата измерений от опорного значения может быть как в минимальную (-), так и в максимальную (+) сторону, то в качестве метрологической характеристики в нормативных документах обычно приводят границы абсолютной или относительной погрешности при доверительной вероятности 95% (Р = 0,95) и тогда такую границу представляют в виде + , например, для абсолютной погрешности.

Для наглядности обратимся к Протоколу. В нем для РИ содержания СВ в ОСР (45,5%) указана погрешность +/-2% (а точнее — ее границы при доверительной вероятности 95%).

Как она была вычислена?

В формулу для оценки границ абсолютной погрешности РИ (см. Таблицу 1, раздел 3, ГОСТ 31640-2012) подставили значение РИ (у = 45,5%), и после округления получили границу погрешности: = +/-2%.

Что это означает на практике?

Среднее значение массовой доли СВ, согласно Протоколу, составляет 45,5%. Реальное (действительное) значение массовой доли сухого вещества в представленном образце корма № 55441/19 находится в границах от 43,5 до 47,5 % при доверительной вероятности (P = 0,95). Это означает, что на 100 повторных результатов измерений одного и того же образца 5 результатов из этой серии даже могут выйти за пределы указанных границ.

Как читать протокол лабораторных исследований с учетом знаний о метрологии

И только теперь, вооружившись необходимыми знаниями, мы может приступить снова к более полному рассмотрению и анализу данных Протокола.

Это, конечно, возможно только в том случае, если такой Протокол отвечает требованиям международного и национального стандарта ГОСТ ИСО/МЭК 17025-2009 ОБЩИЕ ТРЕБОВАНИЯ К КОМПЕТЕНТНОСТИ ИСПЫТАТЕЛЬНЫХ И КАЛИБРОВОЧНЫХ ЛАБОРАТОРИЙ ISO/IEC 17025:2005.

Наш Протокол отвечает этим требованиям.

Выводы из протокола:

1. Если обратиться к тексту нормативного документа ГОСТ 31640-2012 Корма. Методы определения содержания сухого вещества (можно найти в Интернете в свободном доступе), то можно в разделе 3 «Метрологические характеристики» найти формулы расчета границ абсолютной погрешности и убедиться, что погрешность измерения содержания сухого вещества в ОСР составляет 2%!

Таким образом, измеренное значение содержания может реально находится в границах от 43,5 и до 47,5%, а указанное в протоколе значение 45,5% НЕ ЯВЛЯЕТСЯ ТОЧНЫМ, но наиболее вероятным в серии повторных измерений.

Можно также вычислить предел межлабораторной прецизионности (R, %), и он составляет 2,9%. Это показывает насколько МОГУТ ОТЛИЧАТЬСЯ два результата для одного и того же образца, измеренного одним и тем же методом в 2-х разных лабораториях! И оба результата в этом случае надо оценивать как удовлетворяющие требованиям ГОСТ по точности.

1. Если аналогично рассмотреть второй нормативный документ из протокола ГОСТ 32044.1-2012 (ISO 5983-1:2005) КОРМА, КОМБИКОРМА, КОМБИКОРМОВОЕ СЫРЬЕ Определение массовой доли азота и вычисление массовой доли сырого протеина. Часть 1. Метод Къельдаля, то границы погрешностей для определения содержания сырого протеина составят (= +/- 1,2%, а предел межлабораторной прецизионности (R, %), составляет 1,8%.

Таким образом, для массовой доли сырого протеина в этом же образце среднее значение составляет 15,3%, а реальное значение этого показателя находится в пределах границ от 14,1 до 16,5% при доверительной вероятности (P = 0,95).

1. Все вышеуказанные результаты свидетельствуют, что даже самые лучшие мировые лаборатории, выполняющие измерения, не могут обеспечить абсолютную точность результатов своих измерений. И поэтому так важно учитывать погрешность при представлении результатов измерений для объективных оценок их качества. Сделать это возможно, если научиться правильно пользоваться нормативными документами на методы физико-химического анализа и не переоценивать их точности, а объективно воспринимать результаты измерений.

Общее заключение

Из всего вышеизложенного можно заключить:

• В науке и технике не существует абсолютно точных результатов измерений, всегда имеют место погрешности, которые надо правильно оценивать и адекватно воспринимать. Надо помнить: результат измерений носит вероятностный характер, а потому должен укладываться в допускаемые пределы отклонений от среднего.
• Граничные пределы отклонений для различных метрологических характеристик могут быть рассчитаны на основании нормативных документов на методы измерений (в частности, стандарты) или оценены на основании специального метрологического эксперимента – сравнения результатов измерений одних и тех же образцов в различных лабораториях. Допустимыми считаются отклонения, не превышающие граничные по абсолютной величине.
• Надо помнить, что наиболее вероятной оценкой результата измерения будет среднее значение из протоколов двух лабораторий, полученное в условиях воспроизводимости измерений.

Мы благодарим всех наших читателей, кто взял на себя труд дочитать до конца эту статью. В этой публикации мы постарались лишь в общих чертах затронуть подходы к восприятию и оценке результатов лабораторных физико-химических измерений. Если тема метрологии вызовет у нашей аудитории повышенный интерес, мы будем готовы продолжить цикл статей, посвященных проблемам метрологии и правилам организации работ по анализу образцов для обеспечения достоверности результатов их измерений.

С уважением, Владимир Шептун

Автор статьи: Владимир Шептун, к.х.н., методическая поддержка приложений и обслуживание клиентов компании Dinamica Generale S.p.A.в странах СНГ

Условие задачи:

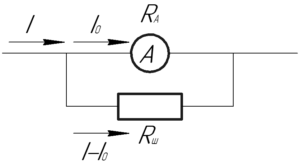
Предел измерения амперметра 5 А, число делений шкалы 100, внутреннее сопротивление 1 Ом. Определить цену деления амперметра, если он включен с шунтом, сопротивление которого 0,02 Ом.

Задача №7.5.17 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(I_0=5) А, (N=100), (R_А=1) Ом, (R_ш=0,02) Ом, (I_{дел}-?)

Решение задачи:

Для измерения силы тока на каком-либо участке электрической цепи используют амперметр, его располагают на том участке, где и нужно измерить величину силы тока. Если предел измерения амперметра (т.е. максимальное значение силы тока, которое может измерить амперметр) не позволяет измерить силу тока на этом участке, то к амперметру параллельно подключают шунт сопротивлением (R_{ш}). Шунт уменьшает силу тока на амперметре.

Чтобы найти цену деления зашунтированного амперметра (I_{дел}), нужно воспользоваться следующей формулой:

[{I_{дел}} = frac{I}{N};;;;(1)]

Так как амперметр и шунт соединены параллельно, то на них одинаковое напряжение (U). Сила тока на амперметре не должна превышать предела измерения (I_0), тогда на шунте сила тока будет равна (left( {I – {I_0}} right)). Здесь (I) – сила тока на том участке, где нужно произвести измерение. Поэтому:

[left{ begin{gathered}
U = {I_0}{R_А} hfill \
U = left( {I – {I_0}} right){R_ш} hfill \
end{gathered} right.]

Тогда, очевидно, имеем:

[{I_0}{R_А} = left( {I – {I_0}} right){R_ш}]

Теперь раскроем скобки в правой части полученного равенства:

[{I_0}{R_А} = I{R_ш} – {I_0}{R_ш}]

[{I_0}{R_А} + {I_0}{R_ш} = I{R_ш}]

[{I_0}left( {{R_А} + {R_ш}} right) = I{R_ш}]

Значит предел измерения (I) зашунтированного амперметра можно найти так:

[I = frac{{{I_0}left( {{R_А} + {R_ш}} right)}}{{{R_ш}}}]

Полученное выражение подставим в формулу (1), так мы получим решение этой задачи в общем виде:

[{I_{дел}} = frac{{{I_0}left( {{R_А} + {R_ш}} right)}}{{N{R_ш}}}]

Посчитаем численный ответ:

[{I_{дел}} = frac{{5 cdot left( {1 + 0,02} right)}}{{100 cdot 0,02}} = 2,55;А]

Ответ: 2,55 А.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

7.5.16 К амперметру с внутренним сопротивлением 0,03 Ом подключен медный шунт длиной 10 см
7.5.18 Вольтметр, внутреннее сопротивление которого 50 кОм, подключенный к источнику
7.5.19 Вольтметр с внутренним сопротивлением 3 кОм, включенный в городскую осветительную сеть