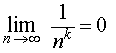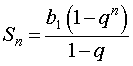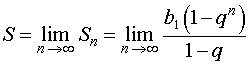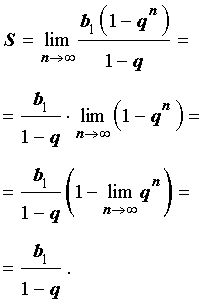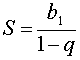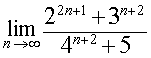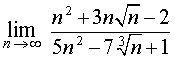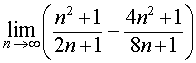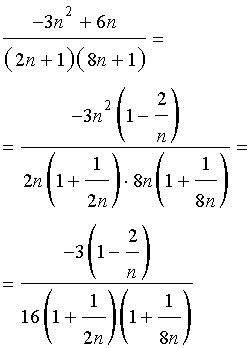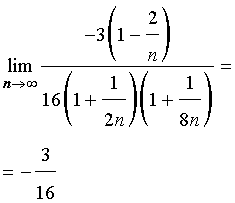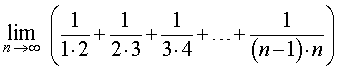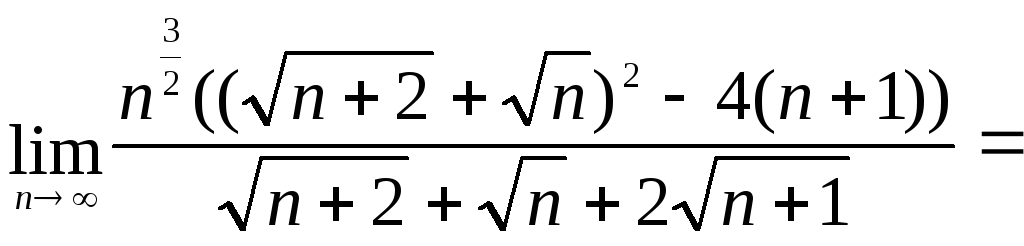Пределы числовых последовательностей
Содержание
Предел числовой последовательности
ОПРЕДЕЛЕНИЕ 1. Число a называют пределом числовой последовательности
a1 , a2 , … an , …
если для любого положительного числа ε найдется такое натуральное число N , что при всех n > N выполняется неравенство
| an – a | < ε .
Условие того, что число a является пределом числовой последовательности
a1 , a2 , … an , … ,
записывают с помощью обозначения
и произносят так: «Предел an при n , стремящемся к бесконечности, равен a ».
То же самое соотношение можно записать следующим образом:
an → a при .
Словами это произносится так: «an стремится к a при n , стремящемся к бесконечности».
ЗАМЕЧАНИЕ. Если для последовательности
a1 , a2 , … an , …
найдется такое число a , что an → a при , то эта последовательность ограничена.
ОПРЕДЕЛЕНИЕ 2. Говорят, что последовательность
a1 , a2 , … an , …
стремится к бесконечности, если для любого положительного числа C найдется такое натуральное число N , что при всех n > N выполняется неравенство
| an| > C .
Условие того, что числовая последовательность
a1 , a2 , … an , … ,
стремится к бесконечности, записывают с помощью обозначения
или с помощью обозначения
при
.
ПРИМЕР 1. Для любого числа k > 0 справедливо равенство
ПРИМЕР 2 . Для любого числа k > 0 справедливо равенство
ПРИМЕР 3. Для любого числа a такого, что | a | < 1, справедливо равенство
ПРИМЕР 4. Для любого числа a такого, что | a | > 1, справедливо равенство
ПРИМЕР 5 . Последовательность
– 1 , 1 , – 1 , 1 , … ,
заданная с помощью формулы общего члена
an = (– 1)n ,
предела не имеет.
Свойства пределов числовых последовательностей
Рассмотрим две последовательности
a1 , a2 , … an , … , и b1 , b2 , … bn , … .
Если при существуют такие числа a и b , что
и
,
то при существуют также и пределы суммы, разности и произведения этих последовательностей, причем
Если, кроме того, выполнено условие
то при существует предел дроби
причем
Для любой непрерывной функции f (x) справедливо равенство
Вывод формулы для суммы членов бесконечно убывающей геометрической прогрессии
Рассмотрим геометрическую прогрессию
b1 , b2 , … bn , … ,
знаменатель которой равен q .
Для суммы первых n членов геометрической прогрессии
Sn = b1 + b2 + … + bn , n = 1, 2, 3, …
справедлива формула
Если для суммы всех членов бесконечно убывающей геометрической прогрессии ввести обозначение
S = b1 + b2 + … + bn + … ,
то будет справедлива формула
В случае бесконечно убывающей геометрической прогрессии знаменатель q удовлетворяет неравенству
| q | < 1 ,
поэтому, воспользовавшись cвойствами пределов числовых последовательностей и результатом примера 3, получаем
Итак,
Примеры вычисления пределов последовательностей. Раскрытие неопределенностей
ОПРЕДЕЛЕНИЕ 3. Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к , то вычисление такого предела называют раскрытием неопределенности типа
.
Часто неопределенность типа удается раскрыть, если и в числителе дроби, и в знаменателе дроби вынести за скобки «самое большое» слагаемое. Например, в случае, когда в числителе и в знаменателе дроби стоят многочлены, «самым большим» слагаемым будет член с наивысшей степенью.
ПРИМЕР 6. Найти предел последовательности
РЕШЕНИЕ. Сначала преобразуем выражение, стоящее под знаком предела, воспользовавшись свойствами степеней:
ОТВЕТ.
ПРИМЕР 7 . Найти предел последовательности
ОТВЕТ.
В следующих двух примерах показано, как можно раскрыть неопределенности типа.
ПРИМЕР 8 . Найти предел последовательности
РЕШЕНИЕ. Сначала преобразуем выражение, стоящее под знаком предела, приводя дроби к общему знаменателю:
Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в каждой из скобок знаменателя дроби:
Теперь, используя cвойства пределов последовательностей и результат примера 1, получаем
ОТВЕТ.
ПРИМЕР 9. Найти предел последовательности
РЕШЕНИЕ. В рассматриваемом примере неопределенность типа возникает за счет разности двух корней, каждый из которых стремится к
. Для того, чтобы раскрыть неопределенность, умножим и разделим выражение, стоящее под знаком предела, на сумму этих корней и воспользуемся формулой сокращенного умножения «разность квадратов».
Из-за большого размера формул подробные вычисления видны только на устройствах с разрешением экрана по ширине не менее 768 пикселей (например, на стационарных компьютерах, ноутбуках и некоторых планшетах). На Вашем мобильном устройстве отображается только результат описанных операций.
Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое из-под каждого корня в знаменателе дроби, а затем сокращая дробь на n2:
Теперь, используя cвойства пределов последовательностей и результат примера 1, получаем
ОТВЕТ.
ПРИМЕР 10. Найти предел последовательности
РЕШЕНИЕ. Замечая, что для всех k = 2, 3, 4, … выполнено равенство
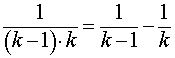
получаем
ОТВЕТ. 1 .
Число e. Второй замечательный предел
Рассмотрим последовательность
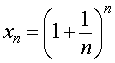 |
(1) |
В дисциплине «Математический анализ», которую студенты естественнонаучных и технических направлений высших учебных заведений изучают на 1 курсе, доказывают, что последовательность (1) монотонно возрастает и ограничена сверху. Из теоремы Вейерштрасса о монотонных и ограниченных последовательностях, доказательство которой выходит за рамки школьного курса математики, вытекает, что последовательность (1) имеет конечный предел. Этот предел принято обозначать буквой e.
Таким образом, справедливо равенство
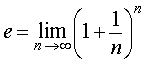 |
(2) |
причем расчеты показывают, что число
e = 2,718281828459045…
и является иррациональным и трансцендентным числом.
Число e играет исключительно важную роль в естествознании и, в частности, служит основанием натуральных логарифмов и основанием показательной функции
y = e x,
которую называют «экспонента».
Число e также является пределом последовательности
|
|
(3) |
что позволяет вычислять число e с любой точностью. Конечно же, доказательство формулы (3) выходит за рамки школьного курса математики.
ЗАМЕЧАНИЕ. Предел (2), в котором для последовательностей раскрывается неопределенность типа , называют вторым замечательным пределом. В разделе нашего справочника «Пределы функций» можно ознакомиться со вторым замечательным пределом для функций.
Сходящиеся последовательности. Бесконечно убывающая геометрическая прогрессия
- Предел последовательности
- Свойства сходящихся последовательностей
- Сумма бесконечно убывающей геометрической прогрессии
- Примеры
п.1. Предел последовательности
Рассмотрим последовательность с $a_n$ = $frac{3n + 1}{n + 1}$ Выделим целую часть у дроби: $$ mathrm{ a_n=frac{(3n+3)-2}{n+1}=frac{3(n+1)}{n+1}-frac{2}{n+1}=3-frac{2}{n+1} } $$ Заполним таблицу:
$$ mathrm{ a_n } $$
$$ mathrm{ 3-frac{2}{2}=2 } $$
begin{gather*} mathrm{ 3-frac{2}{11}=}\ mathrm{=2frac{9}{11} } end{gather*}
begin{gather*} mathrm{ 3-frac{2}{101}=}\ mathrm{=2frac{99}{101} } end{gather*}
begin{gather*} mathrm{ 3-frac{2}{1001}=}\ mathrm{=2frac{999}{1001} } end{gather*}
begin{gather*} mathrm{ 3-frac{2}{10001}=}\ mathrm{=2frac{9999}{10001} } end{gather*}
Чем больше n, тем ближе an к 3.
Этот факт записывают следующим образом: $$ mathrm{ lim_{{n}rightarrowinfty}a_n=lim_{{n}rightarrowinfty}frac{3n+1}{n+1}=3 } $$ и говорят, что число 3 является пределом последовательности {an}.
Число (mathrm{binmathbb{R}}) называют пределом последовательности {an}, если последовательность {an – b} является бесконечно малой, т.е. все её элементы, начиная с некоторого, меньше по модулю любого заранее взятого положительного числа: $$ mathrm{ lim_{{n}rightarrowinfty}a_n=bLeftrightarrow forallvarepsilon gt 0 exists N_{varepsilon}inmathbb{N}: ngeq NRightarrow |a_n-b|lt varepsilon } $$
Раскроем модуль из определения: $$ mathrm{ |a_n-b|lt varepsilon Rightarrow -varepsilon lt a_n-bltvarepsilon Rightarrow b-varepsilonlt a_nlt b-varepsilon } $$ Т.е., начиная с некоторого индекса n, все члены последовательности an (бесконечное множество) попадают в интервал (b – ε; b + ε) – этот промежуток называют ε–окрестностью точки b. Вне этого промежутка находится только первые {a1, a2, …, aN} членов последовательности.
Последовательность, имеющая предел, называется сходящейся.
Последовательность, не имеющая предела, называется расходящейся.
Если предел последовательности (mathrm{ lim_{{n}rightarrowinfty}a_n=0}) последовательность называется бесконечно малой.
Например:
1. Последовательность {an} c (mathrm{ a_n=frac{4n}{n+2}=frac{4(n+2)-8}{n+2}=4-frac{8}{n+2}}) имеет предел (mathrm{ lim_{{n}rightarrowinfty}a_n=4}), значит, является сходящейся.
2. Последовательность {an} c (mathrm{ a_n=4n+2}) при (mathrm{ nrightarrow infty}) также стремится к бесконечности. Предела нет, последовательность расходящаяся.
3. Последовательность {an} c (mathrm{ a_n=frac{1}{n}}) имеет предел (mathrm{ lim_{{n}rightarrowinfty}frac{1}{n}=0}), т.е. является бесконечно малой.
п.2. Свойства сходящихся последовательностей
Свойство 1. Если последовательность имеет предел, то он – единственный.
Свойство 2. Если последовательность имеет предел, то она – ограничена.
Свойство 3. Если все члены последовательности равны a_n=b, то её предел равен b.
Свойство 4. Предел суммы двух последовательностей равен сумме пределов: $$ mathrm{ lim_{{n}rightarrowinfty}(a_n+b_n)=lim_{{n}rightarrowinfty}a_n+lim_{{n}rightarrowinfty}b_n } $$ Свойство 5. Предел произведения двух последовательностей равен произведению пределов: $$ mathrm{ lim_{{n}rightarrowinfty}(a_ncdot b_n)=lim_{{n}rightarrowinfty}a_ncdot lim_{{n}rightarrowinfty}b_n } $$ Свойство 6. Предел частного двух последовательностей равен частному пределов: $$ mathrm{ lim_{{n}rightarrowinfty}left(frac{a_n}{b_n}right)=frac{lim_{{n}rightarrowinfty}a_n}{lim_{{n}rightarrowinfty}b_n} } $$
п.3. Сумма бесконечно убывающей геометрической прогрессии
Рассмотрим геометрическую прогрессию с (mathrm{b_1=1, q=frac12}).
Сумма её первых n членов (см.§27 данного справочника) равна: $$ mathrm{ S_n=b_1frac{1-q^n}{1-q}=1cdotfrac{1-frac{1}{2^n}}{1-frac12}=2left(1-frac{1}{2^n}right)=2-frac{1}{2^{n-1}} } $$ Чем больше будет n, тем меньше будет второе слагаемое (mathrm{frac{1}{2^n-1}}). В пределе (mathrm{ lim_{{n}rightarrowinfty}frac{1}{2^{n-1}}=0, lim_{{n}rightarrowinfty}S_n=2}). Удивительно, но мы нашли сумму бесконечного количества слагаемых; и эта сумма конечна.
Обобщим результат для любого |q| < 1: $$ mathrm{ S=lim_{{n}rightarrowinfty}S_n=lim_{{n}rightarrowinfty}left(b_1frac{1-q^n}{1-q}right)=frac{b_1}{1-q}cdot lim_{{n}rightarrowinfty}left(1-underbrace{q^n}_{rightarrow 0}right)=frac{b_1}{1-q} } $$
Бесконечную геометрическую прогрессию со знаменателем |q| < 1 называют бесконечно убывающей геометрической прогрессией.
Сумма бесконечно убывающей геометрической прогрессии конечна и равна: $$ mathrm{ S=frac{b_1}{1-q} } $$
Например:
Представим периодическую десятичную дробь 0,(16) в виде обыкновенной.
Данную дробь можно записать в виде суммы
0,16161616… = 0,16 + 0,0016 + 0,000016 + …=
= 0,16 + 0,16 · 0,01 + 16 · 0,012+…
Это – сумма бесконечно убывающей геометрической прогрессии с b1 = 0,16, q = 0,01, она равна: (mathrm{S=frac{0,16}{1-0,01}=frac{0,16}{0,99}=frac{16}{99}}), т.е.
(mathrm{0,(16)=frac{16}{99}})
п.4. Примеры
Пример 1. Запишите число в виде обыкновенной дроби:
а) 2,(3) begin{gather*} mathrm{ 2,(3)=2+(0,3+0,03+0,003+…)=2+(0,3+0,3cdot 0,1+0,3cdot 0,1^2+…) }\ mathrm{ b_1=0,3, q=0,1 }\ mathrm{ S=frac{b_1}{1-q}=frac{0,3}{1-0,1}=frac{0,3}{0,9}=frac13, 2,(3)=2+frac13=2frac13 } end{gather*}
б) 5,(17) begin{gather*} mathrm{ 5,(17)=5+(0,17+0,0017+0,000017+…)= }\ mathrm{ =5+(0,17+0,17cdot 0,01+0,17cdot 0,01^2+…) }\ mathrm{ b_1=0,17, q=0,01 }\ mathrm{ S=frac{b_1}{1-q}=frac{0,17}{1-0,01}=frac{0,17}{0,99}=frac{17}{99}, 5,(17)=5+frac{17}{99}=5frac{17}{99} } end{gather*}
Пример 2. Найдите сумму бесконечно убывающей геометрической прогрессии:
a) (mathrm{1, frac{1}{sqrt{2}}, frac12,…})
(mathrm{b_1=1, q=frac{1}{sqrt{2}}}) begin{gather*}mathrm{ S=frac{b_1}{1-q}=frac{1}{frac{1}{sqrt{2}}}=frac{sqrt{2}}{sqrt{2}-1}=frac{sqrt{2}(sqrt{2}+1)}{(sqrt{2}-1)(sqrt{2}+1)}=frac{2+sqrt{2}}{2-1}=2+sqrt{2} } end{gather*}
б) 1, π – 3, (π – 3)2, …
b1 = 1, q = π – 3 begin{gather*} mathrm{ S=frac{b_1}{1-q}=frac{1}{1-(pi-3)}=frac{1}{4-pi} } end{gather*}
Пример 3. Решите уравнение begin{gather*} mathrm{ 1+2x+x^2-x^3+x^4-x^5+…=frac{13}{6}, text{если} |x|lt 1 } end{gather*} Выделим геометрическую прогрессию: begin{gather*} mathrm{ 3x+(1-x+x^2-x^3+x^4-x^5+…)=frac{13}{6} }\ mathrm{ b_1=1, q=-x, S=frac{b_1}{1-q}=frac{1}{1+x} } end{gather*} Получаем: begin{gather*} mathrm{ 3x+frac{1}{1+x}=frac{13}{6}Rightarrow frac{3x(1+x)+1}{1+x}=frac{13}{6}Rightarrow 6(3x^2+3x+1)=13(1+x)Rightarrow }\ mathrm{ Rightarrow 18x^2+5x-7=0 }\ mathrm{ D=5^2-4cdot 18cdot (-7)=25+504=529=23^2, x=frac{-5pm 23}{36}= left[ begin{array}{ l } mathrm{x_1=-frac79} & \ mathrm{x_2=frac12} & end{array}right. } end{gather*} Оба ответа удовлетворяют ограничению |x| < 1.
Ответ: (mathrm{x_1=-frac79; x_2=frac12})
Пример 4. В квадрат со стороной a вписан второй квадрат так, что его вершины являются серединами сторон первого квадрата. А во второй квадрат точно так же вписан третий квадрат, и т.д. Найдите 1) сумму периметров всех квадратов; 2) сумму площадей всех квадратов.
Сторона первого квадрата b1 = a. Сторона второго квадрата равна половине диагонали первого квадрата (mathrm{b_2=frac{1sqrt{2}}{2}=frac{a}{sqrt{2}}}). Сторона третьего квадрата равна половине стороны первого квадрата (mathrm{b_3=frac{a}{2}}), и т.д.
Получаем геометрическую прогрессию со знаменателем (mathrm{q=frac{1}{sqrt{2}}}).
Периметры квадратов линейно зависят от длин сторон: $$ mathrm{ p_1=4a, p_2=4cdotfrac{a}{sqrt{2}}=2sqrt{2}a, p_3=4cdotfrac{a}{2}=2a,… } $$ Для геометрической прогрессии периметров знаменатель будет тем же: (mathrm{q=frac{1}{sqrt{2}}}).
$$ mathrm{ S_p=frac{p_1}{1-q}=frac{4a}{1-frac{1}{sqrt{2}}}=frac{4sqrt{2}a}{sqrt{2}-1}=frac{4sqrt{2}a(sqrt{2}+1)}{(sqrt{2}-1)(sqrt{2}+1)}=frac{4a(2+sqrt{2})}{2-1}=4a(2+sqrt{2}) } $$ Площади квадратов имеют квадратичную зависимость от длин сторон: $$ mathrm{ s_1=a^2, s_2=left(frac{a}{sqrt{2}}right)^2=frac{a^2}{2}, s_3=left(frac{a}{2}right)^2=frac{a^2}{4},… } $$ Для геометрической прогрессии площадей знаменатель будет равен квадрату знаменателя для прогрессии сторон: (mathrm{q_s=q^2=left(frac{1}{sqrt{2}}right)^2=frac12}).
Сумма всех площадей: begin{gather*} mathrm{ S_s=frac{s_1}{1-q_s}=frac{a^2}{1-frac12}=2a^2} end{gather*} Интересно, что сумма площадей всех(!) квадратов внутри самого большого равна площади этого самого большого квадрата.
Ответ: (mathrm{S_p=4a(2+sqrt{2}), S_s=2a^2})
Пример 5*. В окружность радиуса r вписан правильный треугольник, в треугольник вписана другая окружность, в которую снова вписан правильный треугольник, и т.д. Найдите сумму периметров всех треугольников и сумму длин всех окружностей. 
Сторона правильного треугольника, вписанного в первую окружность: (mathrm{a_1=2rcdot sin 60^{circ}=sqrt{3}r}).
Радиус второй окружности, вписанной в первый треугольник: (mathrm{r_2=frac{a_1}{2}tg30^{circ}=frac{a_1}{2sqrt{3}}=frac{sqrt{3}r}{2sqrt{3}}=frac{r}{2}})
Сторона правильного треугольника, вписанного во вторую окружность: (mathrm{a_2=sqrt{3}r_2=frac{sqrt{3}r}{2}}).
Радиус третьей окружности, вписанной во второй треугольник: (mathrm{r_3=frac{r_2}{2}=frac{r}{4}}).
Получаем геометрическую прогрессию для сторон треугольников: $$ mathrm{ a_1=sqrt{3}r, a_2=frac{sqrt{3}r}{2}, a_3=frac{sqrt{3}r}{4}=,…, q=frac12 } $$ и геометрическую прогрессию для радиусов окружностей: $$ mathrm{ r_1=r, r_2=frac{r}{2}, r_3=frac{r}{4},…, q=frac12 } $$ Геометрическая прогрессия для периметров треугольников: $$ mathrm{ p_1=3a_1=3sqrt{3}r, p_2=frac{3sqrt{3}r}{2}, p_3=frac{3sqrt{3}r}{4},…, q=frac12 } $$ Сумма всех периметров: begin{gather*} mathrm{ S_p=frac{p_1}{1-q}=2p_1=6sqrt{3}r} end{gather*} Геометрическая прогрессия для длин всех окружностей: $$ mathrm{ L_1=2pi r_2=2pi r, L_2=pi r, L_3=frac{pi r}{2},…, frac12 } $$ Сумма всех длин окружностей: $$ mathrm{ S_L=frac{L_1}{1-q}=2L_1=4pi r } $$ Ответ: (mathrm{S_p=6sqrt{3}r, S_L=4pi r})
1. Предел числовой последовательности
Числовой
последовательностью
называют правило, по которому каждому
натуральному числу
ставится
в соответствие действительное
(комплексное) число.
Последовательность обозначают символом(
).
Можно сказать, что последовательность
является функцией(
).Числовую
последовательность задают формулойn-го
члена:
.
Например, еслито
,
,
… и т.д.
Числовую
последовательность также можно задать
рекуррентным соотношением:
,
.
Тогда
,
,
и т.д.
Пример
Арифметическая
прогрессия ‑ числовая
последовательность, в которой каждый
член, начиная со второго, отличается от
предыдущего на одно и то же число
,
называемое разностью прогрессии:.
Любая арифметическая прогрессия имеет
вид
Общий член
арифметической прогрессии определяется
так:
.
Арифметическая
прогрессия применяется при выполнении
финансово-коммерческих расчетов, когда
при начислении дивидендов, прибыли и
т.д. используются простые проценты .
Пример
Первого марта 2008
г. некто положил в банк сумму в 500 тыс.
рублей из расчета 60 процентов годовых.
Известно, что сумма вклада растет линейно
(простые проценты). Какова сумма вклада
на 1 июля того же года?
►Для ответа на
поставленный вопрос обозначим через
сумму вклада
в начальный момент (в данном случае 1-го
марта), через год и на момент времени
соответственно.
Тогда из условия задачи получаем
,
где— учетная ставка (в данном случаеa = 0,6).
Из полученного уравнения следует, что
.
Значение суммы вклада на момент времени
можно получить
из уравнения прямой, проходящей через
две точки
и
:
,
откуда следует

где.
Поскольку в данном примере=
,
то значение суммы вклада на 1 июля
составит 500(1+0,61/3)
= 5001,2
= 600 (тыс.руб.). ◄
Пример
Геометрическая
прогрессия ‑ числовая
последовательность, в которой каждый
член, начиная со второго, отличается от
предыдущего на один и тот же множитель
,
называемый знаменателем прогрессии.
Любая геометрическая прогрессия имеет
вид
Общий член
геометрической прогрессии определяется
по формуле
.
Геометрическая
прогрессия применяется при выполнении
финансово-коммерческих расчетов, когда
при начислении дивидендов, прибыли и
т. д. используются сложные проценты.
Пример
Банк ежемесячно
производит перерасчет суммы вклада,
начисляя дополнительную сумму,
пропорциональную значению текущего
счета. Через сколько месяцев первоначальная
сумма вклада удвоится?
►Обозначим через
исумму вклада
в начальный момент и через
месяцев соответственно. Тогда
по
условию
задачи
имеем:
,
,
,
где
‑ заданная учетная ставка (100
%,
если учетная ставка измеряется в
процентах).
Таким образом,
последовательные значения суммы вклада
на конец
—го
месяца
образуют
геометрическую прогрессию, общий член
которой имеет следующий вид:
.
Из полученного
соотношения следует, что если
,
то для нахождения соответствующего
значения
нужно решить
уравнение
.
Логарифмируя это уравнение по основаниюе, получим
,
откуда
следует
.
Если, например, ежемесячно начисляется
5%, то=0.05,
и для
получаем
=14.2.
Итак, через 15 месяцев сумма вклада
увеличится более чем вдвое (через 14
месяцев она увеличится в 1.0514=1.98
раз, а через 15 месяцев ‑ в 2.08 раз по
сравнению с первоначальной).◄
Очевидным образом
определяются сумма,
произведение, частное двух
последовательностей.
Мы будем иметь дело лишь с последовательностями
действительных чисел.
Число
называетсяпределом
последовательности
если для любого
найдётся номер
такой, что для любого
выполняется неравенство
.
При этом пишутили
и говорят, что последовательность
сходится к числу
.
Геометрически это
означает, что для любой O
(,
)
найдётся такой номер,
что всеприn
>
будут принадлежать этой
–окрестности.
(> 0
(n
>
O
(,
))).
Если=C
= const,
то
=C,
т.к.
= 0 <
для любыхn.
Чтобы найти предел
последовательности, используя только
его определение, следует поступить так:
-
предположить, что
предел равен
;
-
решить неравенство
<
относительноn
для любого
> 0;
-
если решение
неравенства имеет вид n
>
,
то предположение, что предел равен,
верно и предел найден.
ТЕОРЕМА 1.
Если последовательность имеет предел,
то он единственный.
Свойства предела.
Если
,
,
то:
1)
;
2)
;
3)
;
4)
при (
).
Последовательность
называетсябесконечно
малой, если
.
Последовательность
называетсябесконечно
большой,
если для любого
найдётся
номерn0
такой, что для любого
справедливо неравенство
;
записывается это так:.
Если при этом,
начиная с некоторого номера, сохраняют
положительный (отрицательный) знак, то
пишут(
)
. Если последовательность имеет конечный
предел, то она называется сходящейся.
В противном случае – расходящейся.
Последовательность
называетсянеубывающей,
если
для любогоn.
Если
,
– то этоневозрастающая
последовательность. Невозрастающая и
неубывающая последовательности
называются монотонными.
Если неравенства строгие (<
,
>
),
то последовательности называются
строго монотонными.
ТЕОРЕМА 2.
Монотонная ограниченная последовательность
сходится.
Важную роль играет
последовательность
Доказывается, что эта последовательность
сходится, и ее предел обозначается
буквой е; е2,718.
Типовой пример
Доказать, пользуясь
определением предела последовательности,
что
.
►Имеем:
.
Решив неравенство
,
получими ясно, что достаточно выбрать
,
чтобы длянеравенство
выполнялось для всех
.
Что и требовалось.
Типовой пример
Дана последовательность
. Найдите:
1);
2)такое, что для всех
выполняется неравенство
.
1)
►Имеем
.
2)
►Найдём требуемое
.
Из проделанных выше выкладок следует,
чтодолжно быть подобрано так, чтобы для
всех
или
;
отсюда следует
,
.
Следовательно, можно взять.
Предел отношения
многочленов
Пусть xn
и yn
многочлены от n
степени k
и m
соответственно, т.е.
xn=Pk(n)=a0
nk+a1nk-1+…+ak,
yn=Qm(n)=b0nm+b1nm-1+…+bm
Докажем, что предел
отношения многочленов равен пределу
отношения их старших членов, т.е.

Имеем:

что и требовалось.
Итак,

Типовые
примеры
Найти пределы:
1)
►Раскроем скобки,
приведем подобные и воспользуемся
приемом из предыдущего примера
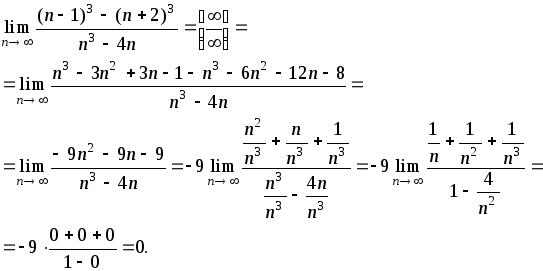
2)
.
►.◄
3).
►.
◄
4)
.
►.◄
Следует отметить,
что полученные формулы справедливы не
только для многочленов целой степени,
но и для многочленов дробной степени,
так как
для любогоa>0.
При вычислении
пределов, в которых присутствуют суммы
арифметической или геометрической
прогрессии, используются формулы
для суммы арифметической прогрессии и
для суммы геометрической прогрессии.
Типовые примеры
1)
.►

2)

=[используем формулу
суммы геометрической прогрессии]= =
3)
►В
данном выражении участвует функция n!
(читается n—факториал),
которая определяется равенством
Имеем
,

4)

►В числителе три слагаемых соответственно
степени:Следовательно, степень числителя равна
,
а главный член в числителе равен.
Аналогично, главный член в знаменателеИмеем:

5)

►
6)
.
►
◄
7)

►.
Как видите, идея
о главном старшем члене здесь также
дает быстрое решение.
Обычно этот предел
вычисляется так:



►
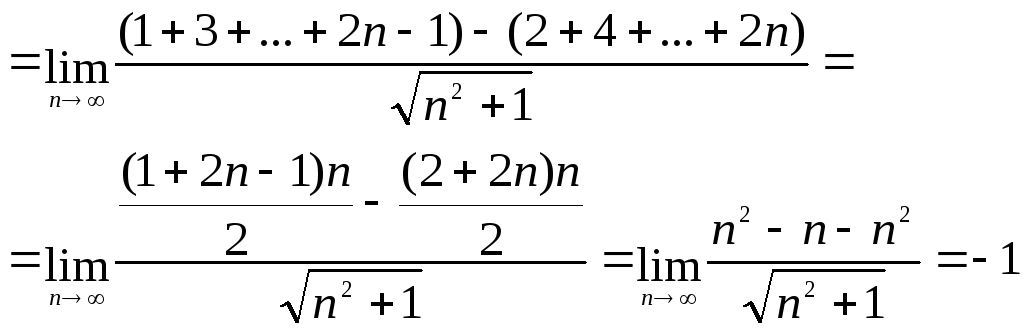
9)

► Напомним:
.
Имеем:
.◄
Для избавления от
неопределенности
здесь следует избавиться от иррациональности
в числителе, умножив и разделив данное
выражение на соответствующее сопряженное
выражение.
Типовые
примеры
(неопределенности
).
1)
.
►Используем формулу
Для данного примера
Имеем:
◄
2)
.
►Напоминаем, чтои при
.
Имеем:
=
3)
.
►
◄
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Покажем, что . По определению:
Рассмотрим неравенство в конце:
Вынесем степень за знаки модуля (см. прото-задачу П-ссылка):
Прологарифмируем это неравенство по основанию . Так как основание , то знак неравенства меняется на противоположный:
Какое бы мы не взяли, нам достаточно взять любое число, большее и тогда требуемое по определению предела неравенство будет выполняться.
Но нам нужно не любое число, а натуральное, поэтому выбирать будем по следующей формуле:
Докажем, что такое будет подходить определению доказываемого предела.
По этой формуле мы берем , если логарифм окажется отрицательным:
Если логарифм окажется положительным, то получаем его округление сверху («потолок»). Из определения «потолка» числа:
Следующее натуральное число после будет , поэтому
Итак, мы показали, что любые натуральные подходят определению доказываемого предела.
Значит мы доказали по определению, что:
Теперь вернемся к исходному пределу:
Выносим константу из предела: