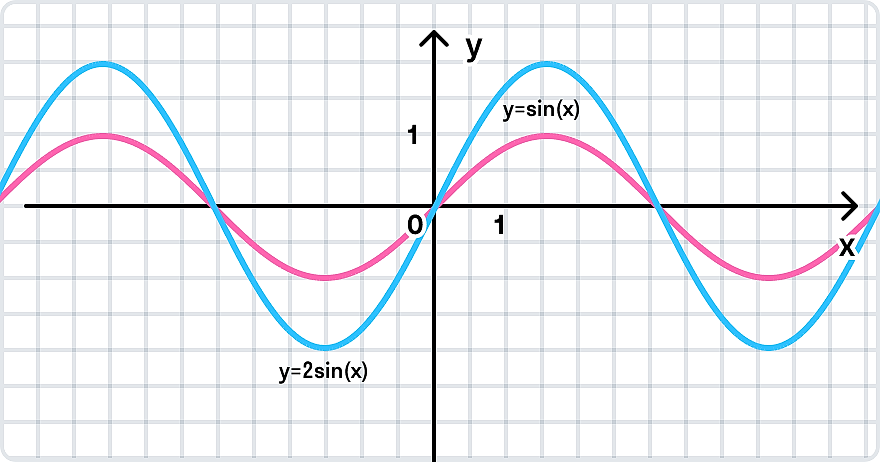
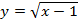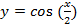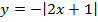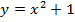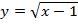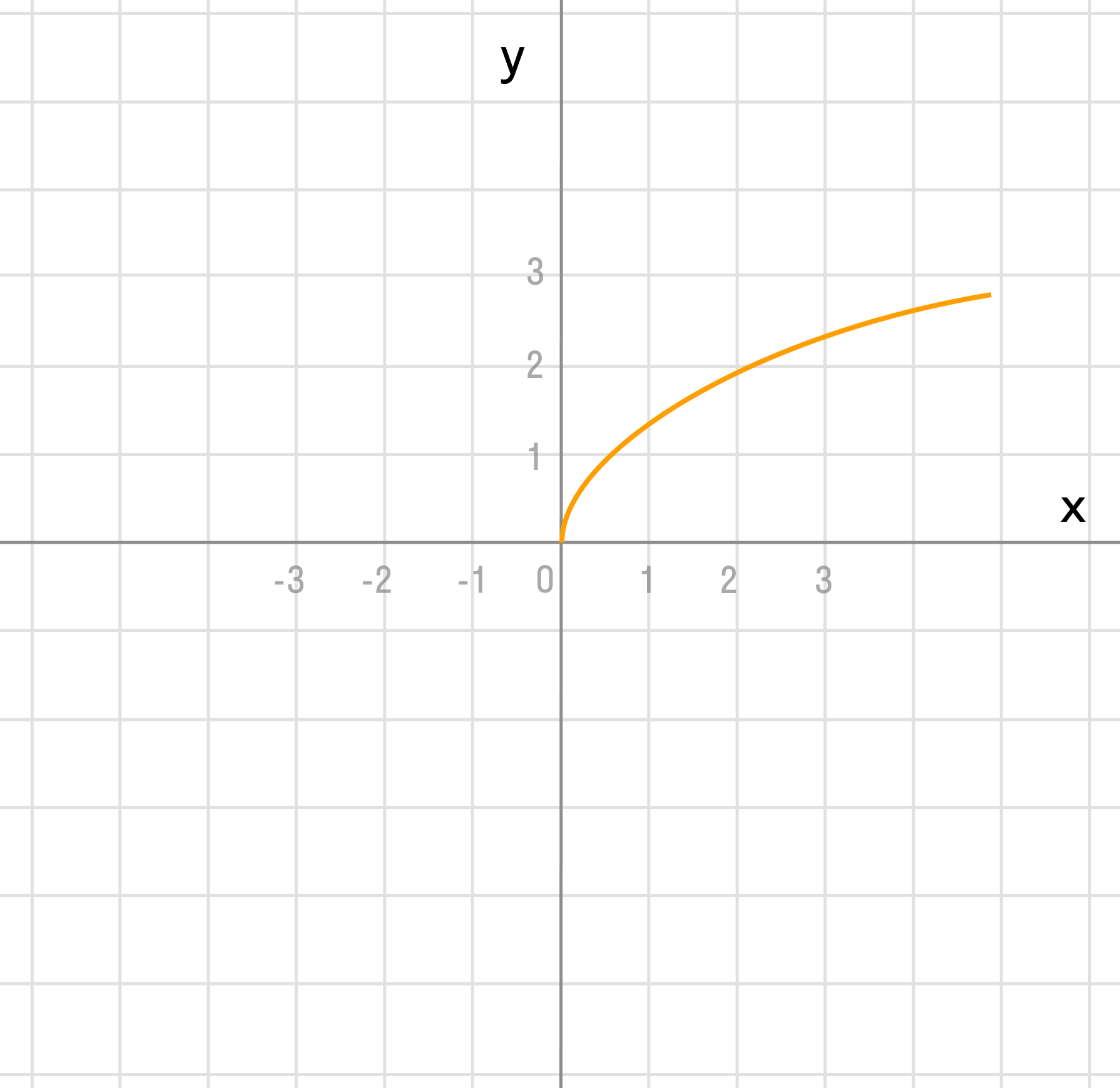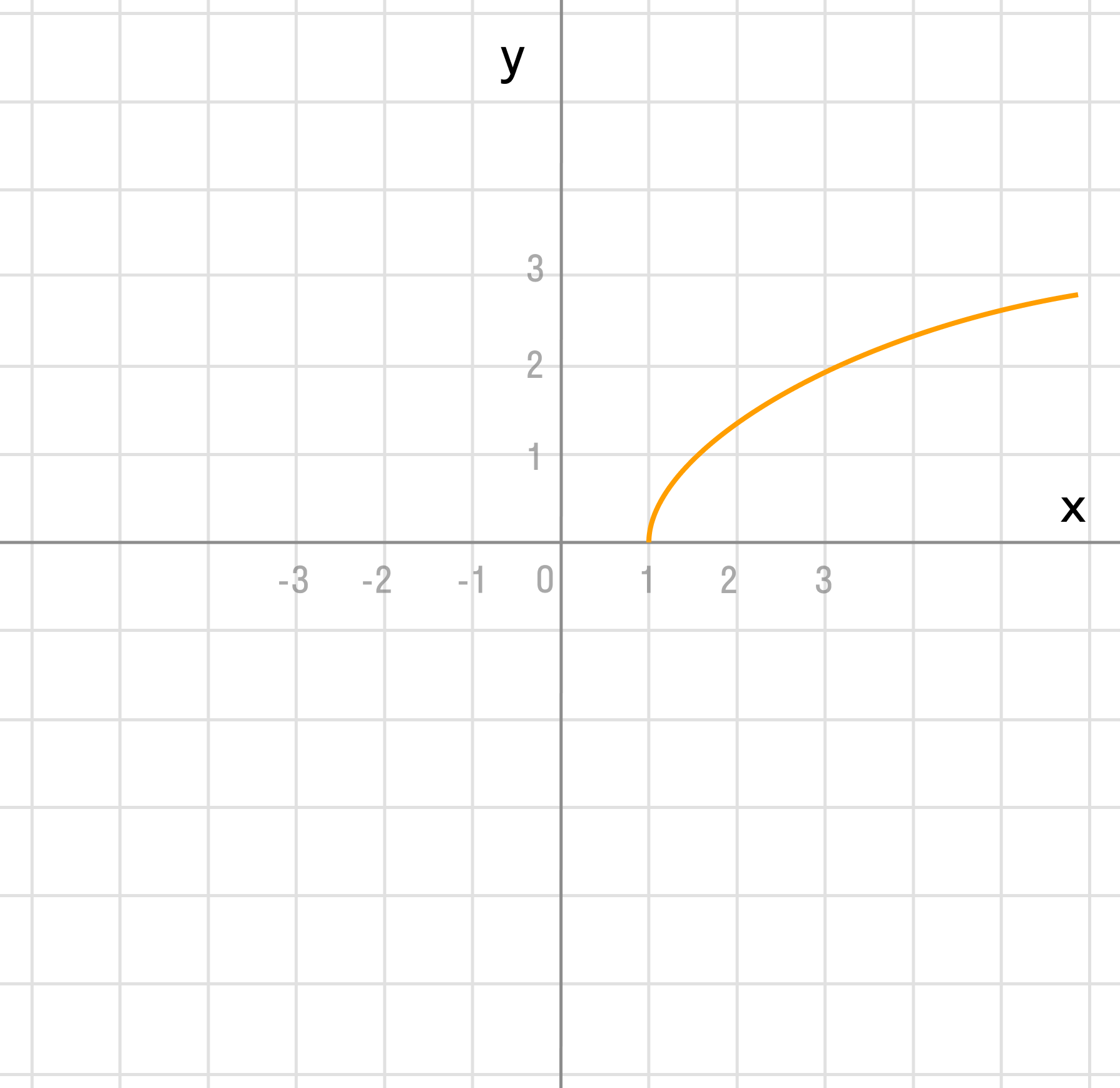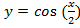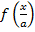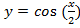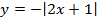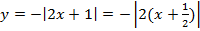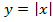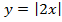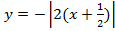Понятие функции
Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие значения функции. Вот, какими способами ее можно задать:
-
Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
-
Графический способ — наглядно.
-
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
-
Словесный способ.
Область определения функции — это множество всех допустимых значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Например, для функции вида
область определения выглядит так
-
х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): (-∞; 0) ⋃ (0; +∞).
Область значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): [0; +∞).
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
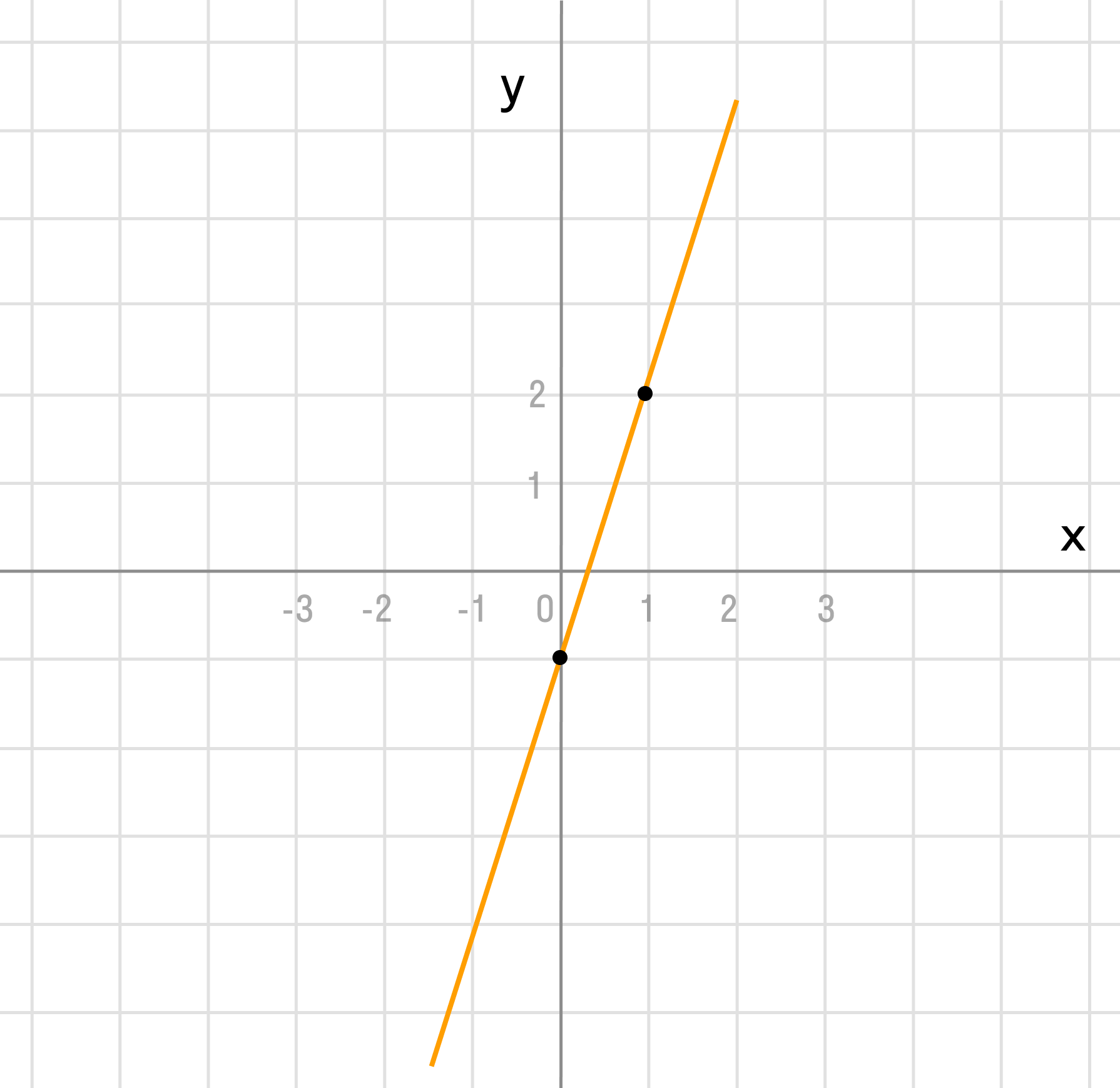
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
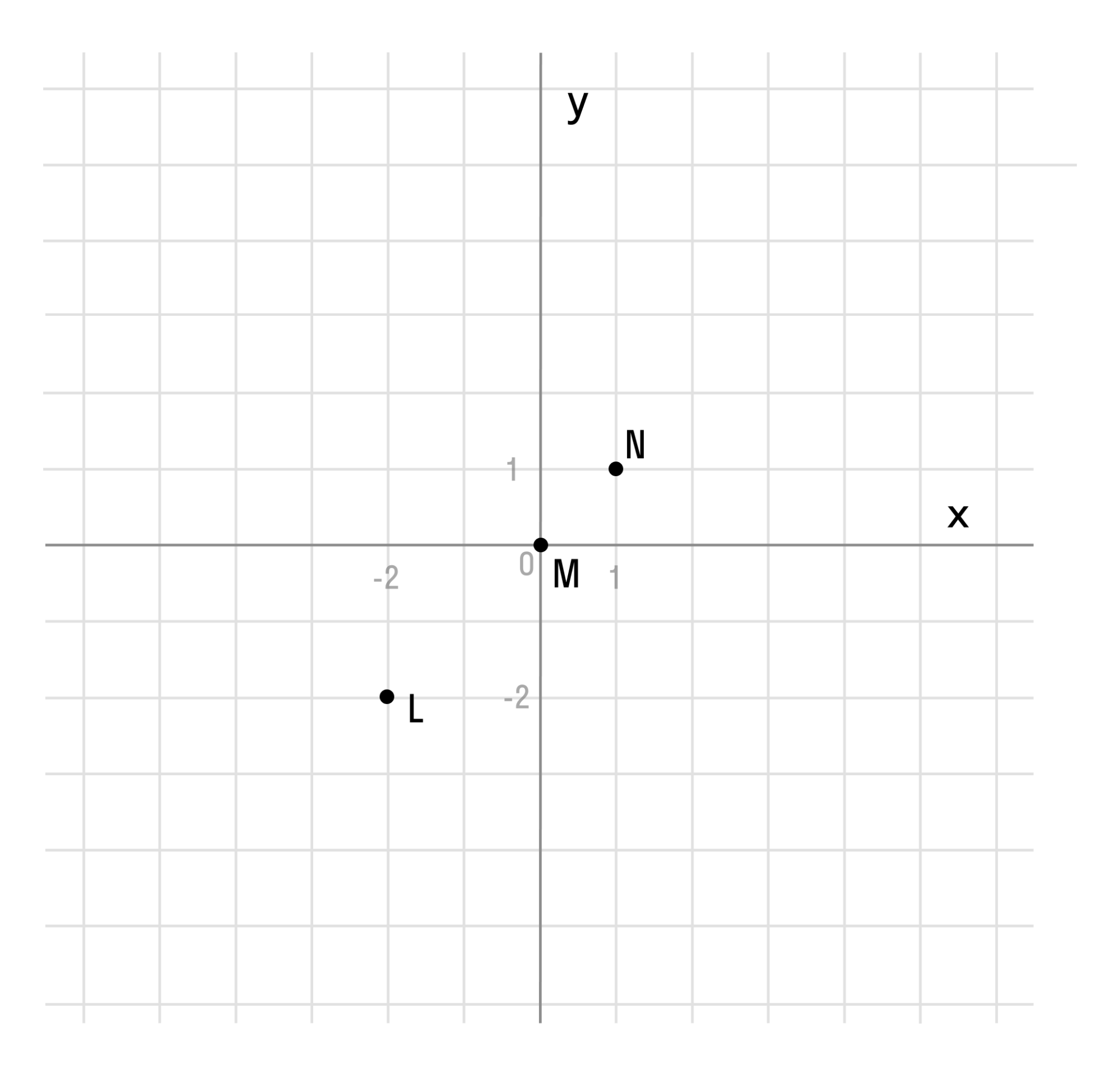
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться при решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Запоминаем!
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.
Исследование функции
Важные точки графика функции y = f(x):
-
стационарные и критические точки;
-
точки экстремума;
-
нули функции;
-
точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых значение функции равно нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
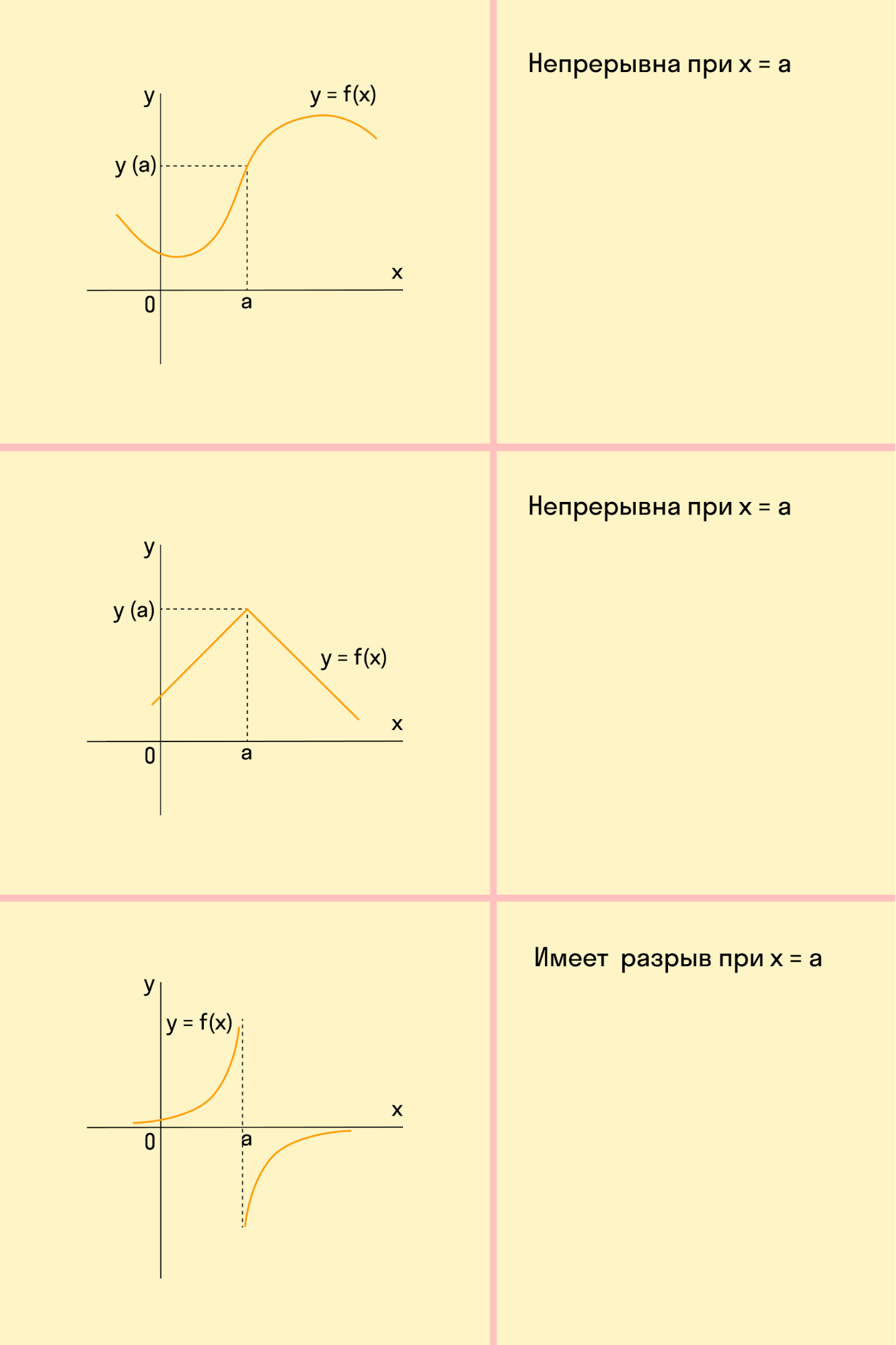
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
-
Найти область определения функции.
-
Найти область допустимых значений функции.
-
Проверить не является ли функция четной или нечетной.
-
Проверить не является ли функция периодической.
-
Найти точку пересечения с осью OY (если она есть).
-
Вычислить производную и найти критические точки, определить промежутки возрастания и убывания.
-
Промежутки знакопостоянства.
-
Асимптоты.
-
На основании проведенного исследования построить график функции.
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах или воспользуйтесь онлайн тренажером.
Задача 1. Построим график функции
Как решаем:
Упростим формулу функции:
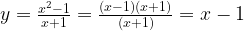
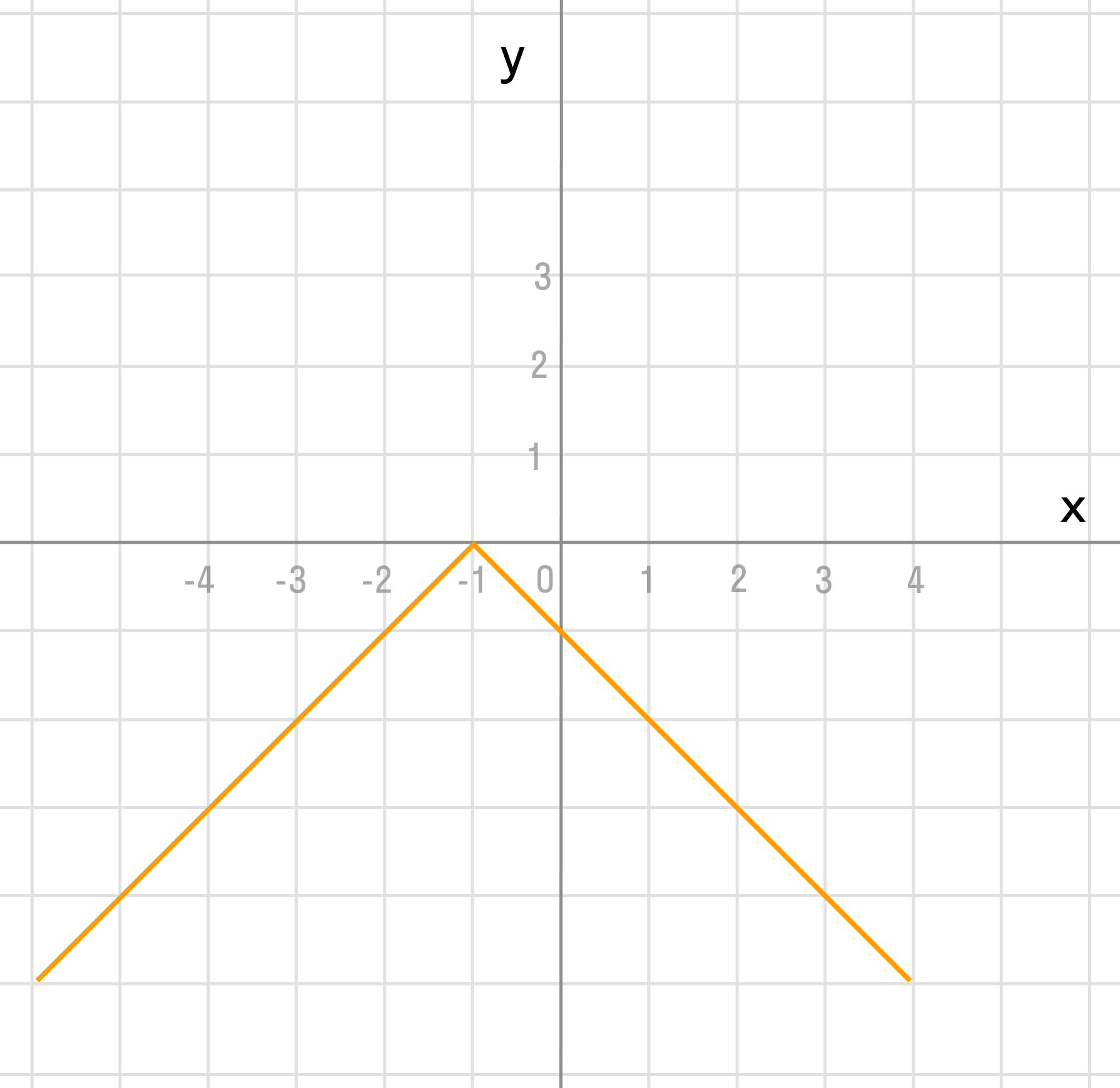
График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).
Задача 2. Построим график функции
Как решаем:
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Задача 3. Построить графики функций:
а) y = 3x — 1
б) y = -x + 2
в) y = 2x
г) y = -1
Как решаем:
Воспользуемся методом построения линейных функций «по точкам».
а) y = 3x — 1
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
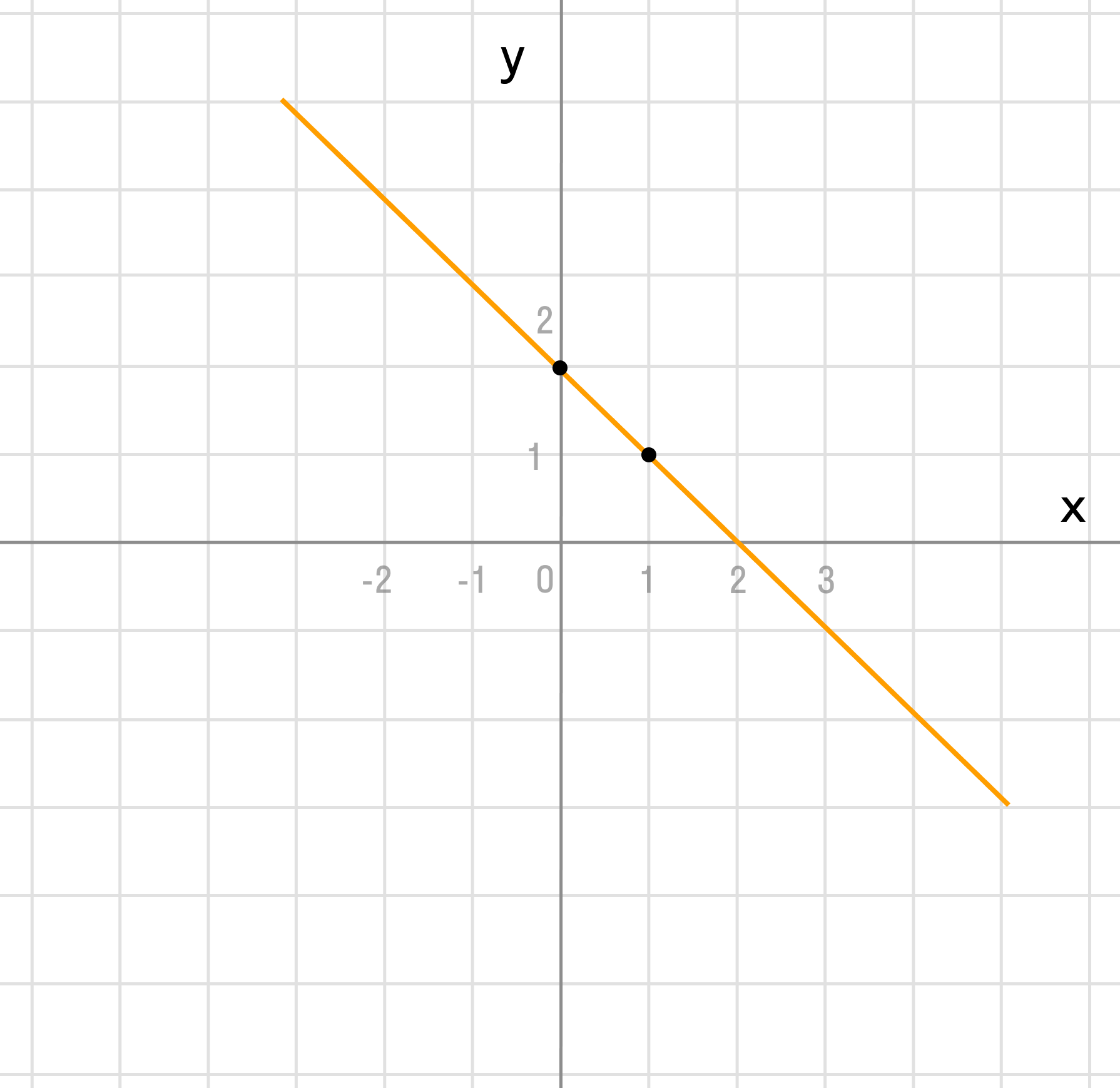
б) y = -x + 2
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
в) y = 2x
k = 2 > 0 — угол наклона к оси Ox острый, b = 0 — график проходит через начало координат.
г) y = -1
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
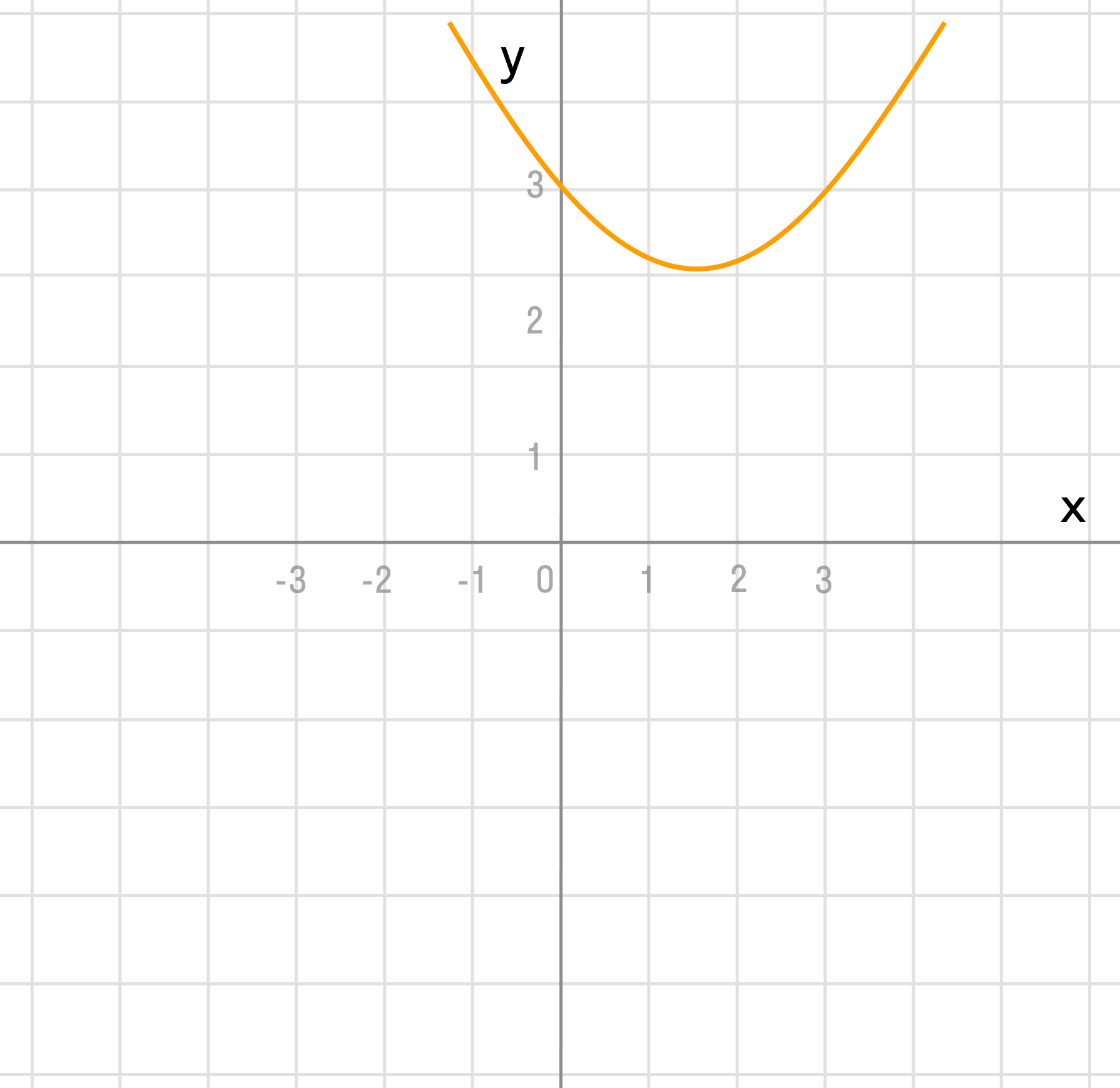
Задача 4. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Как решаем:
Вспомним, как параметры a, b и c определяют положение параболы.
-
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины
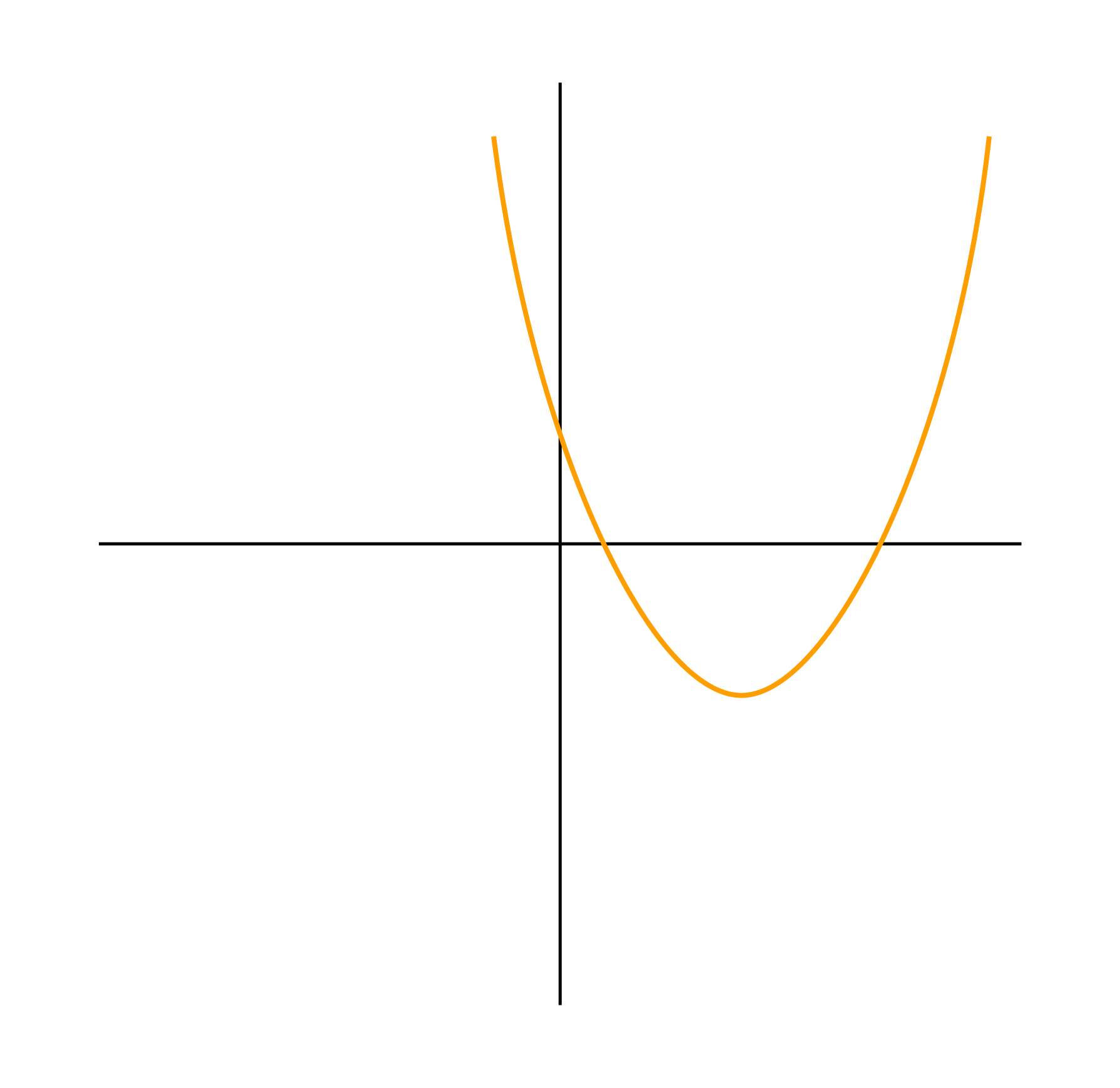
-
Ветви вверх, следовательно, a > 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
-
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
Задача 5. Построить графики функций:
а) y = x² + 1
б)
в) y = (x — 1)² + 2
г)
д)
Как решаем:
Построить графики можно при помощи элементарных преобразований.
Если построен график функции y = f(x), то при a > 0 следующие графики получаются с помощью сдвига графика f(x).
-
y = f(x) + a — график функции y = f(x) сдвигается на a единиц вверх;
-
y = f(x) − a — график функции y = f(x) сдвигается на a единиц вниз;
-
y = f(x + a) — график функции y = f(x) сдвигается на a единиц влево;
-
y = f(x − a) — график функции у = f(x) сдвигается на a единиц вправо.
Преобразование график по типу y = mf(x): y = f(x) → y = mf(x), где m — положительное число.
-
Если m > 1, то такое преобразование графика называют растяжением вдоль оси y с коэффициентом m.
-
Если m < 1, то такое преобразование графика называют сжатием к оси x с коэффициентом 1/m.
а)
Преобразование в одно действие типа f(x) + a.
y = x²
Сдвигаем график вверх на 1:
y = x² + 1
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
в) y = (x — 1)² + 2
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
y = x²
Сдвигаем график вправо на 1:
y = (x — 1)²
Сдвигаем график вверх на 2:
y = (x — 1)² + 2
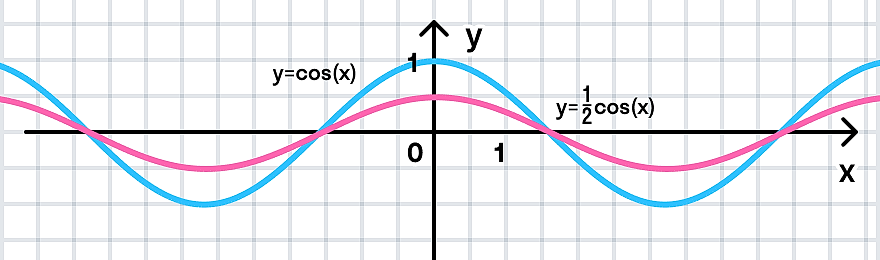
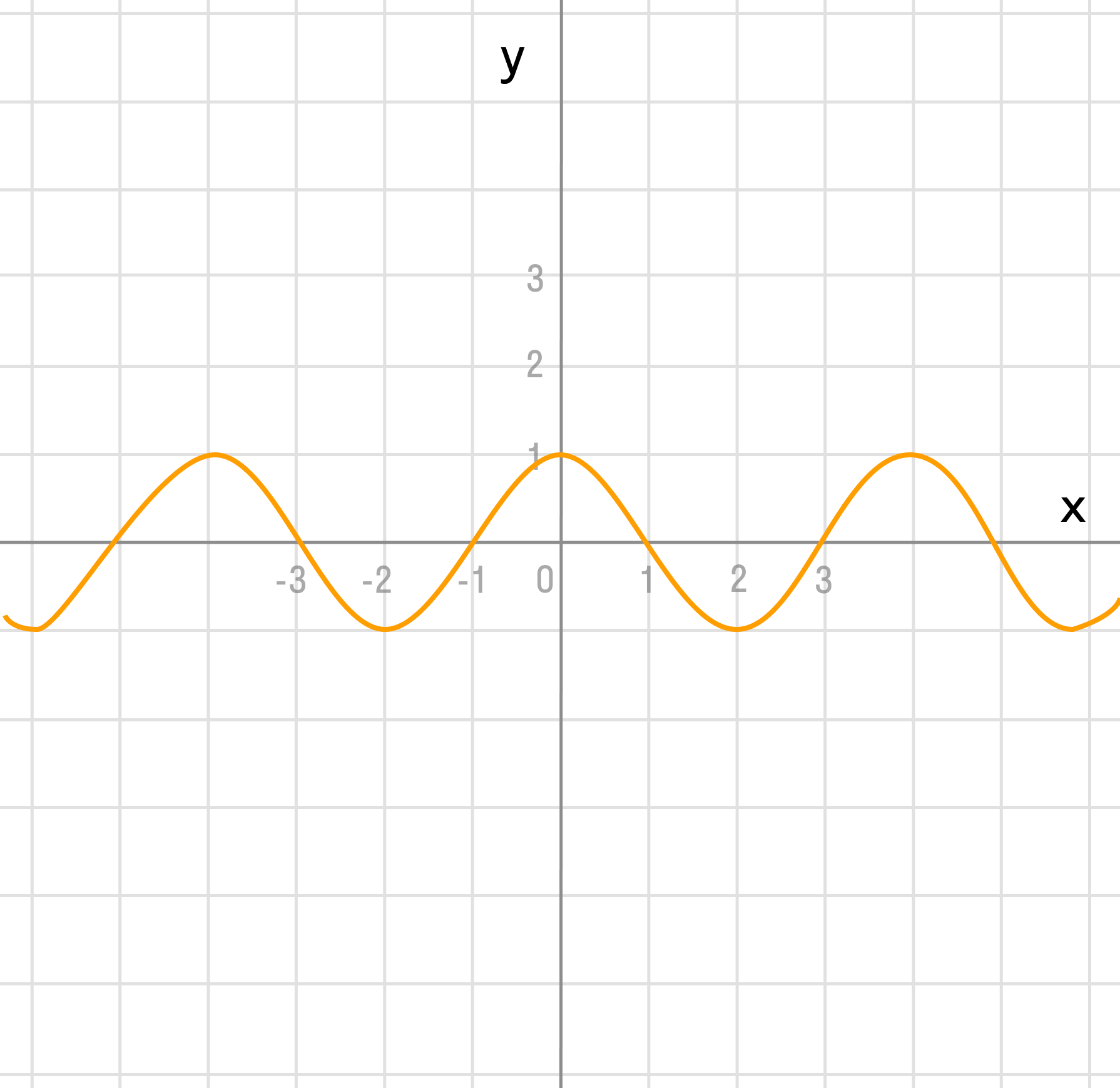
г)
Преобразование в одно действие типа
y = cos(x)
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
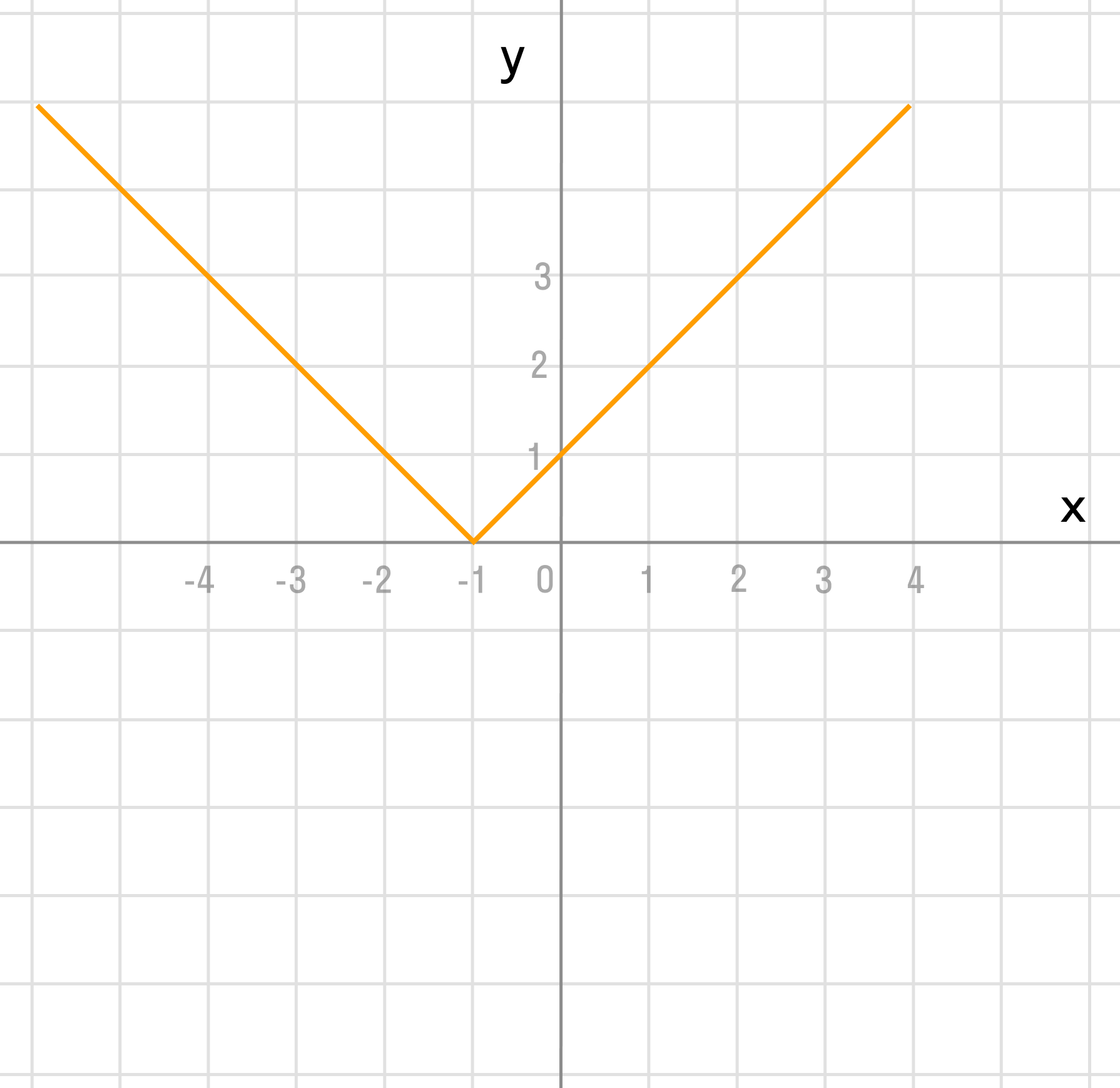
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция
Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Если a > 0 , прямая будет проходить через I и III координатные четверти.
b – точка пересечения прямой с осью y .
Если a < 0 , прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y .
Если a = 0 , функция принимает вид y = b .
Отдельно выделим график уравнения x = a .
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».
Парабола
Графиком функции y = a x 2 + b x + c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a > 0 , ветки параболы направлены вверх.
- Если a < 0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти x в – координату вершины параболы.
x в = − b 2 a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D > 0 – две точки пересечения.
- Если D = 0 – одна точка пересечения.
- Если D < 0 – нет точек пересечения.



Гипербола
Графиком функции y = k x является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.
Если k < 0, ветви гиперболы проходят через II и IV четверти.
Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .
Квадратный корень
Функция y = x имеет следующий график:
Возрастающие/убывающие функции
Функция y = f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
Функция y = f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.
Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.
Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Скачать домашнее задание к уроку 5.
Download Article
Download Article
A graph of a function is a visual representation of a function’s behavior on an x-y plane. Graphs help us understand different aspects of the function, which would be difficult to understand by just looking at the function itself. You can graph thousands of equations, and there are different formulas for each one. That said, there are always ways to graph a function if you forget the exact steps for the specific type of function.
-
1
Recognize linear functions as simple, easily-graphed lines, like
. There is one variable and one constant, written as
in a linear function, with no exponents, radicals, etc. If you’ve got a simple equation like this, then graphing the function is easy.[1]
Other examples of linear functions include: -
2
Use the constant to mark your y-intercept. The y-intercept is where the function crosses the y-axis on your graph. In other words, it is the point where
. So, to find it, you simply set x to zero, leaving the constant in the equation alone. For the earlier example,
, your y-intercept is 5, or the point (0,5). On your graph, mark this spot with a dot.[2]
Advertisement
-
3
Find the slope of your line with the number right before the variable. In your example,
, the slope is «2.» That is because 2 is right before the variable in the equation, the «x.» Slope is how steep a line is, or how high the line goes before going to the right or left. Bigger slopes mean steeper lines.
-
4
Break the slope into a fraction. Slope is about steepness, and steepness is simply the difference between movement up and down and movement left and right. Slope is a fraction of rise over run. How much does the line «rise» (go up) before it «runs» (goes to the side)? For the example, the slope of «2» could be read as
.[3]
- If the slope is negative, that means the line goes down as you move to the right.
-
5
Starting at your y-intercept, follow your «rise» and «run» to graph more points. Once you know your slope, use it to plot out your linear function. Start at your y-intercept, here (0,5), and then move up 2, over 1. Mark this point (1,7) as well. Find 1-2 more points to create an outline of your line.[4]
-
6
Use a ruler to connect your dots and graph your linear function. To prevent mistakes or rough graphs, find and connect at least three separate points, though two will do in a pinch. This is the graph of your linear equation![5]
Advertisement
-
1
Determine the function. Get the function of the form like f(x), where y would represent the range, x would represent the domain, and f would represent the function. As an example, we’ll use y = x+2, where f(x) = x+2.[6]
-
2
Draw two lines in a + shape on a piece of paper. The horizontal line is your x axis. The vertical line is your y axis.
-
3
Number your graph. Mark both the x axis and the y axis with equally-spaced numbers. For the x axis, the numbers are positive on the right side and negative on the left side. For the y axis, the numbers are positive on the upper side and negative on the lower side.[7]
-
4
Calculate a y value for 2-3 x values. Take your function f(x) = x+2. Calculate a few values for y by putting the corresponding values for x visible on the axis into the function. For more complicated equations, you may want to simplify the function by getting one variable isolated first.[8]
- -1: -1 + 2 = 1
- 0: 0 +2 = 2
- 1: 1 + 2 = 3
-
5
Draw the graph point for each pair. Simply sketch imaginary lines vertically for each x axis value and horizontally for each y axis value. The point where these lines intersect is a graph point.[9]
-
6
Remove the imaginary lines. Once you have drawn all the graph points, you can erase the imaginary lines. Note: the graph of f(x) = x would be a line parallel to this one passing through the origin (0,0), but f(x) = x+2 is shifted two units up (along the y-axis) on the grid because of the +2 in the equation.[10]
Advertisement
-
1
-
2
Find any zeros first. Zeros, also called x-intercepts, are the points where the graph crosses the horizontal line on the graph. While not all graphs even have zeros, most do, and it is the first step you should take to get everything on track. To find zeros, simply the entire function to zero and solve. For example:
-
3
Find and mark any horizontal asymptotes, or places where it is impossible for the function to go, with a dotted line. This is usually points where the graph does not exist, like where you are dividing by zero. If your equation has a variable in a fraction, like
, start by setting the bottom of the fraction to zero. Any places where it equals zero can be dotted off (in this example, a dotted line at x=2 and x=-2), since you cannot ever divided by zero. Fractions, however, are not the only places you can find asymptotes. Usually, all you need is some common sense:
-
4
Plug in and graph several points. Simply pick a few values for x and solve the function. Then graph the points on your graph. The more complicated the graph, the more points you’ll need. In general, -1, 0, and 1 are the easiest points to get, though you’ll want 2-3 more on either side of zero to get a good graph.[13]
- For the equation
, you might plug in -1,0,1, -2, 2, -10, and 10. This gives you a nice range of numbers to compare.
- Be smart selecting numbers. In the example, you’ll quickly realize that having a negative sign doesn’t matter — you can stop testing -10, for example, because it will be the same as 10.
- For the equation
-
5
Map the end behavior of the function to see what happens when it is really huge. This gives you an idea of the general direction of a function, usually as a vertical asymptote. For example — you know that eventually,
gets really, really big. Just one additional «x» (one million vs. one million and one) makes y much bigger. There are a few ways to test end behavior, including:
-
6
Connect the dots, avoiding asymptotic and following the end behavior to graph an estimate of the function. Once you have 5-6 points, asymptotes, and a general idea of end behavior, plug it all in to get an estimated version of the graph.[15]
-
7
Get perfect graphs using a graphing calculator. Graphing calculators are powerful pocket computers that can give exact graphs for any equation. They allow you to search exact points, find slope lines, and visualize difficult equations with ease. Simply input the exact equation into the graphing section (usually a button labeled «F(x) = «) and hit graph to see your function at work.
Advertisement
Add New Question
-
Question
How do I sketch a graph of a square root function?
The process is the same as shown in the article above except, of course, it involves calculating (or estimating) the square roots of certain values.
-
Question
How do I graph function y = -2 sin(2/3x)?
Choose a value for x. Find 2/3 of that value. Then use a trigonometry table to find the sine of that last value. Then multiply the sine by -2. That gives you the value of y that corresponds to the chosen value of x. Do this again for other x values, and you will then have several x-y pairs to form the graph of the function.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If you are ever completely lost with what to do, start plugging in points. You could technically graph the entire function like this if you tried infinite combinations of numbers.
-
Graphing calculators are a great way to practice. Try to graph by hand, then use the calculator to get a perfect image of the graph and see how you did.
Advertisement
References
About This Article
Article SummaryX
To graph a function, start by plugging in 0 for x and then solving the equation to find y. Then, mark that spot on the y-axis with a dot. Next, find the slope of the line, which is the number that’s right before the variable. Once you know your slope, write it as a fraction over 1 and then use the rise over run to plot the rest of the points from the spot you marked on the y-axis. Finally, use a ruler to draw a line connecting all of the points on your graph. To learn how to graph complicated functions by hand, scroll down!
Did this summary help you?
Thanks to all authors for creating a page that has been read 138,763 times.
Did this article help you?
Функции и их графики — одна из самых увлекательных тем в школьной математике. Жаль только, что проходит она… мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, — линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.
Умение строить графики функций необходимо для решения задач с параметрами на ЕГЭ по математике. Это одна из первых тем курса математического анализа в вузе. Это настолько важная тема, что мы в ЕГЭ-Студии проводим по ней специальные интенсивы для старшеклассников и учителей, в Москве и онлайн. И часто участники говорят: «Жаль, что мы не знали этого раньше».
Но это не все. Именно с понятия функции и начинается настоящая, «взрослая» математика. Ведь сложение и вычитание, умножение и деление, дроби и пропорции — это все-таки арифметика. Преобразования выражений — это алгебра. А математика — наука не только о числах, но и о взаимосвязях величин. Язык функций и графиков понятен и физику, и биологу, и экономисту. И, как сказал Галилео Галилей, «Книга природы написана на языке математики».
Точнее, Галилео Галилей сказал так:«Математика есть алфавит, посредством которого Господь начертал Вселенную».
Темы для повторения:
Понятие функции
Типы элементарных функций
Преобразования графиков функций
Производная функции
Асимптоты. Поведение функции в бесконечности
1. Построим график функции
Знакомая задача! Такие встречались в вариантах ОГЭ по математике. Там они считались сложными. Но сложного ничего здесь нет.
Упростим формулу функции:
при
График функции — прямая с выколотой точкой
2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, применяемый в решении неравенств, построении графиков и оценке целых величин в задачах на числа и их свойства. Он встретится вам также на первом курсе, когда придется брать интегралы.
3. Построим график функции
Он получается из графика функции растяжением в 2 раза, отражением по вертикали и сдвигом на 1 вверх по вертикали
4. Построим график функции
Главное — правильная последовательность действий. Запишем формулу функции в более удобном виде:
Действуем по порядку:
1) График функции y=sinx сдвинем на влево;
2) сожмем в 2 раза по горизонтали,
3) растянем в 3 раза по вертикали,
4) сдвинем на 1 вверх
Сейчас мы построим несколько графиков дробно-рациональных функций. Чтобы лучше понять, как мы это делаем, читайте статью «Поведение функции в бесконечности. Асимптоты».
5. Построим график функции
Область определения функции:
Нули функции: и
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Прямая x = 0 (ось Y) — вертикальная асимптота функции. Асимптота — прямая, к которой бесконечно близко подходит график функции, но не пересекает ее и не сливается с ней (смотри тему «Поведение функции в бесконечности. Асимптоты»)
Есть ли другие асимптоты у нашей функции? Чтобы выяснить это, посмотрим, как ведет себя функция, когда x стремится к бесконечности.
Раскроем скобки в формуле функции:
Если x стремится к бесконечности, то стремится к нулю. Прямая
является наклонной асимптотой к графику функции.
6. Построим график функции
Это дробно-рациональная функция.
Область определения функции
Нули функции: точки — 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты:
Если x стремится к бесконечности, то у стремится к 1. Значит, — горизонтальная асимптота.
Вот эскиз графика:
Еще один интересный прием — сложение графиков.
7. Построим график функции
Если x стремится к бесконечности, то стремится к нулю и график функции будет бесконечно близко подходить к наклонной асимптоте
Если x стремится к нулю, то функция ведет себя как Это мы и видим на графике:
Вот мы и построили график суммы функций. Теперь график произведения!
8. Построим график функции
Область определения этой функции — положительные числа, поскольку только для положительных x определен
Значения функции равны нулю при (когда логарифм равен нулю), а также в точках, где
то есть при
При
значение cos x равно единице. Значение функции в этих точках будет равно
при
9. Построим график функции
Функция определена при Она четная, поскольку является произведением двух нечетных функций
и
График симметричен относительно оси ординат.
Нули функции — в точках, где то есть при
при
Если x стремится к бесконечности, стремится к нулю. Но что же будет, если x стремится к нулю? Ведь и x, и sin x будут становиться меньше и меньше. Как же будет вести себя частное
?
Оказывается, что если x стремится к нулю, то стремится к единице. В математике это утверждение носит название «Первого замечательного предела».
А как же производная? Да, наконец-то мы до нее добрались. Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.
10. Построим график функции
Область определения функции — все действительные числа, поскольку
Функция нечетна. Ее график симметричен относительно начала координат.
При x=0 значение функции равно нулю. При значения функции положительны, при
отрицательны.
Если x стремится к бесконечности, то стремится к нулю.
Найдем производную функции
По формуле производной частного,
если
или
В точке производная меняет знак с «минуса» на «плюс»,
— точка минимума функции.
В точке производная меняет знак с «плюса» на «минус»,
— точка максимума функции.
Найдем значения функции при x=2 и при x=-2.
Графики функций удобно строить по определенному алгоритму, или схеме. Помните, вы изучали ее в школе?
Общая схема построения графика функции:
1. Область определения функции
2. Область значений функции
3. Четность — нечетность (если есть)
4. Периодичность (если есть)
5. Нули функции (точки, в которых график пересекает оси координат)
6. Промежутки знакопостоянства функции (то есть промежутки, на которых она строго положительна или строго отрицательна).
7. Асимптоты (если есть).
8. Поведение функции в бесконечности
9. Производная функции
10. Промежутки возрастания и убывания. Точки максимума и минимума и значения в этих точках.
Графики функций с модулями
Покажем полезные примеры построения графиков модулей функций. Такие графики с модулями встречаются на ЕГЭ в задачах с параметрами.
11. Построим графики функций:
а)
б)
в)
Решение:
а) Первый график построить легко. Выделим полный квадрат в формуле функции
График – квадратичная парабола, сдвинутая на 3 влево и на 1 вверх и перевернутая ветвями вниз.
б) Чтобы построить график функции зеркально отражаем относительно оси Х те части первого графика, которые лежали под ней. А та часть первого графика, которая лежала выше оси Х, остается на месте. Точки (2; 0) и (4; 0), в которых график пересекал ось Х, также остаются на месте.
в) Теперь график функции
Он тоже получается из графика первой функции, но преобразования другие. Часть первого графика, лежащая справа от оси Y, остается на месте. Действительно, модуль неотрицательного числа равен самому этому числу. Получили график функции для неотрицательных . И отражаем его зеркально относительно оси Y в левую полуплоскость.
12. Построим график функции
Функция определена при всех действительных х.
Нули функции:
Функция получается из элементарной функции в результате следующих преобразований:
1) Сдвиг на 2 единицы вниз,
2) Отражение части графика, лежащей ниже оси ОХ, в верхнюю полуплоскость. Стандартный прием при построении графика модуля функции.
13. Построим график функции
Ее график получается из графика функции сдвигом на 5 единиц вниз вдоль оси ОУ и симметричным отображением части графика, лежащей ниже оси ОХ, в верхнюю полуплоскость.
– вертикальная асимптота графика,
— горизонтальная асимптота.
Читайте также: Асимптоты. Поведение функции в бесконечности
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Построение графиков функций» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
07.05.2023
п.1. Алгоритм исследования и построения графика функции
1. Найти область определения функции, классифицировать точки разрыва
2. Исследовать функцию на четность и периодичность
3. Провести анализ асимптотического поведения функции (наличие вертикальных, горизонтальных и наклонных асимптот) (см. §41 данного справочника)
4. Взять первую производную. Определить критические точки, интервалы монотонности, точки экстремума
5. Взять вторую производную. Определить критические точки 2-го порядка, интервалы выпуклости и точки перегиба
6. Найти точки пересечения функции с осями координат (если уравнение (f(x)=0) не имеет аналитического решения, указать количество точек пересечения с осью OX)
7. Построить график функции
п.2. Примеры
Пример 1. Постройте график функции (y=2x^3-6x^2-18x+7)
1) Область определения (xinmathbb{R})
Точек разрыва нет
2) Четность begin{gather*} f(-x)=2(-x)^3-6(-x)^2-18(-x)+7ne left[ begin{array}{l} f(x)\ -f(x) end{array} right. end{gather*} Функция ни четная, ни нечетная.
Периодичность: функция не периодическая
3) Асимптоты
1. Вертикальных асимптот нет, т.к. нет точек разрыва 2-го рода
2. Горизонтальные асимптоты: begin{gather*} b_1=lim_{xrightarrow -infty}2x^3-6x^2-18x+7=-infty\ b_2=lim_{xrightarrow +infty}2x^3-6x^2-18x+7=+infty\ end{gather*} Пределы бесконечны, горизонтальных асимптот нет.
3. Наклонные асимптоты: begin{gather*} k_1=lim_{xrightarrow -infty}frac{2x^3-6x^2-18x+7}{x}=+infty\ k_2=lim_{xrightarrow +infty}frac{2x^3-6x^2-18x+7}{x}=+infty\ end{gather*} Пределы бесконечны, наклонных асимптот нет.
4) Первая производная begin{gather*} f'(x)=2cdot 3x^2-6cdot 2x-18cdot 1+0=6x^2-12x-18=6(x^2-2x-3)=\ =6(x-3)(x+1)\ f'(x)=0 text{при} left[ begin{array}{l} x=3\ x=-1 end{array} right. end{gather*} Критические точки: (x=-1) и (x=3)
Составляем таблицу:
| (x) | ((-infty;-1)) | -1 | (-1;3) | 3 | ((3;+infty)) |
| (f'(x)) | >0 | 0 | <0 | 0 | >0 |
| (f(x)) | (nearrow) | max | (searrow) | min | (nearrow) |
Функция возрастает при (xin(-infty;-1)cup(3;+infty))
Функция убывает при (xin(-1;3))
Точка максимума (x=-1; y_{max}=f(-1)=-2-6+18+7=17)
Точка минимума (x=3; y_{min}=f(3)=54-54-54+7=-47)
5) Вторая производная: begin{gather*} f»(x)=(6x^2-12x-18)’=6cdot 2x-12cdot 1-0=12x-12=12(x-1)\ f»(x)=0 text{при} x=1 end{gather*} Критическая точка 2-го порядка: (x=1)
Составляем таблицу:
| (x) | ((-infty;1)) | 1 | ((1;+infty)) |
| (f»(x)) | <0 | 0 | >0 |
| (f(x)) | (cap) | перегиб | (cup) |
Функция выпуклая вверх при (xin(-infty;1))
Функция выпуклая вниз при (xin(1;+infty))
Точка перегиба (x=1; f(1)=2-6-18+7=-15)
6) Точки пересечения с осями координат
Пересечение с осью OY: (x=0, y=7)
Пересечение с осью OX: $$ 2x^3-6x^2-18x+7=0 $$ У кубической параболы точка максимума (-1;17), точка минимума (3;-47).
Т.к. (y_{max}gt 0, y_{min}lt 0) кубическая парабола пересекает ось OX в трех точках: $$ x_1lt -1, -1lt x_2lt 3, x_3gt 3 $$
7) График
Пример 2. Постройте график функции (y=frac3x+frac x3)
1) Область определения
ОДЗ: (xne 0)
(x=0) — точка разрыва. Исследуем односторонние пределы: begin{gather*} lim_{xrightarrow -0}left(frac 3x+frac x3right)=frac{3}{-0}+0=-infty, lim_{xrightarrow +0}left(frac 3x+frac x3right)=frac{3}{+0}+0=+infty end{gather*} Пределы не равны и бесконечны. (x=0) — точка разрыва 2-го рода.
2) Четность $$ f(-x)=frac{3}{-x}+frac{-x}{3}=-left(frac 3x+frac x3right)=-f(x) $$ Функция нечётная.
Периодов нет. Функция не периодическая.
3) Асимптоты
1. Вертикальная асимптота (x=0) – точка разрыва 2-го рода
2. Горизонтальные асимптоты begin{gather*} b_1=lim_{xrightarrow -infty}left(frac 3x+frac x3right)=0+(-infty)=-infty\ b_2=lim_{xrightarrow +infty}left(frac 3x+frac x3right)=0+(+infty)=+infty end{gather*} Пределы бесконечны, горизонтальных асимптот нет.
3. Наклонные асимптоты: begin{gather*} k_1=frac1x lim_{xrightarrow -infty}left(frac 3x+frac x3right)=lim_{xrightarrow -infty}left({3}{x^2}+frac13right)=0+frac13=frac13\ k_1=frac1x lim_{xrightarrow +infty}left(frac 3x+frac x3right)=lim_{xrightarrow +infty}left({3}{x^2}+frac13right)=0+frac13=frac13\ k=k_1=k_2=frac13 end{gather*} Ищем b: $$ b=lim_{xrightarrow infty}(y-kx)=lim_{xrightarrow infty}left(frac3x+frac x3-frac x3right)=lim_{xrightarrow infty}frac 3x=0 $$ Есть одна наклонная асимптота (y=frac 3x)
Кривая стремится к ней на минус и плюс бесконечности.
4) Первая производная: begin{gather*} f'(x)=-frac{3}{x^2}+frac13=frac{x^2-9}{3x^2}=frac{(x+3)(x-3)}{3x^2}\ f'(x)=0 text{при} x=pm 3 end{gather*} Критические точки: (x=left{0;pm 3right})
Составляем таблицу:
| (x) | ((-infty;-3)) | -3 | (-3;0) | 0 | ((0;3)) | 3 | ((3+infty)) |
| (f'(x)) | >0 | 0 | <0 | (varnothing) | <0 | 0 | >0 |
| (f(x)) | (nearrow) | max | (searrow) | (varnothing) | (searrow) | min | (nearrow) |
Функция возрастает при (xin(-infty;-3)cup(-3;+infty))
Функция убывает при (xin(-3;0)cup(0;3))
Точка максимума (x=-3; y_{max}=f(-3)=-1-1=-2)
Точка минимума (x=3; y_{min}=f(3)=1+1=2)
5) Вторая производная: begin{gather*} f»(x)=frac13left(1-frac{9}{x^2}right)’=frac13left(0+frac{9cdot 2}{x^3}right)=frac{6}{x^3} end{gather*} Вторая производная нулей не имеет.
Критическая точка 2-го порядка: (x=0)
Составляем таблицу:
| (x) | ((-infty;0)) | 0 | ((0;+infty)) |
| (f»(x)) | <0 | (varnothing) | >0 |
| (f(x)) | (cap) | (varnothing) | (cup) |
Функция выпуклая вверх при (xin(-infty;0))
Функция выпуклая вниз при (xin(0;+infty))
Точек перегиба нет.
6) Точки пересечения с осями
Пересечение с осью OY: (x=0notin D) — не входит в ОДЗ, пересечений с OY нет
Пересечение с осью OX:
(frac3x+frac x3=0Rightarrow frac{9+x^2}{3x}=0Rightarrow xin varnothing) — решений нет, пересечений с OX нет
7) График
Пример 3*. Постройте график функции (y=frac{x^3-4}{(x-1)^3})
Сколько корней имеет уравнение (frac{x^3-4}{(x-1)^3}=a)?
1) Область определения
ОДЗ: (xne 1)
(x=1) — точка разрыва. Исследуем односторонние пределы: begin{gather*} lim_{xrightarrow 1-0}frac{x^3-4}{(x-1)^3}=frac{1-4}{(1-0-1)^3}=frac{-3}{-0}=+infty\ lim_{xrightarrow 1+0}frac{x^3-4}{(x-1)^3}=frac{1-4}{(1+0-1)^3}=frac{-3}{+0}=-infty end{gather*} Пределы не равны и бесконечны. (x=1) — точка разрыва 2-го рода.
2) Четность $$ f(-x)=frac{(-x)^3-4}{(-x-1)^3}ne left[ begin{array}{l} f(x)\ -f(x) end{array} right. $$ Функция ни четная, ни нечетная.
Периодичность: функция не периодическая
3) Асимптоты
1. Вертикальная асимптота (x=1) – точка разрыва 2-го рода
2. Горизонтальные асимптоты begin{gather*} b_1=lim_{xrightarrow -infty}frac{x^3-4}{(x-1)^3}=left[frac{infty}{infty}right]=lim_{xrightarrow -infty}frac{x^3left(1-frac{4}{x^3}right)}{x^3left(1-frac{1}{x^3}^3right)}=frac{1-0}{(1-0)^3}=1\ b_2=lim_{xrightarrow +infty}frac{x^3-4}{(x-1)^3}=left[frac{infty}{infty}right]=lim_{xrightarrow +infty}frac{x^3left(1-frac{4}{x^3}right)}{x^3left(1-frac{1}{x^3}^3right)}=frac{1-0}{(1-0)^3}=1\ b=b_1=b_2=1 end{gather*} Одна горизонтальная асимптота: (y=1)
Функция стремится к ней на минус и плюс бесконечности.
3. Наклонные асимптоты: begin{gather*} k_1=lim_{xrightarrow infty}frac{x^3-4}{x(x-1)^3}=left[frac{infty}{infty}right]=lim_{xrightarrow infty}frac{x^4left(frac1x-frac{4}{x^4}right)}{x^4left(1-frac{1}{x^3}^3right)}=frac{0-0}{(1-0)^3}=0 end{gather*} Угловой коэффициент (k=0). Наклонных асимптот нет.
4) Первая производная: begin{gather*} f'(x)=left(frac{x^3-4}{(x-1)^3}right)’=frac{3x^2(x-1)^3-(x^3-4)cdot 3(x-1)^2}{(x-1)^6}=frac{3x^2(x-1)-3(x^3-4)}{(x-1)^4}=\ =frac{3x^3-3x^2-3x^3+12}{(x-1)^4}=frac{-3(x^2-4)}{(x-1)^4}=frac{-3(x-2)(x+2)}{(x-1)^4}\ f'(x)=0 text{при} x=pm 2 end{gather*} Критические точки: (x=left{1;pm 2right})
Составляем таблицу:
| (x) | ((-infty;-2)) | -2 | (-2;1) | 1 | ((1;2)) | 2 | ((2+infty)) |
| (f'(x)) | <0 | 0 | >0 | (varnothing) | >0 | 0 | <0 |
| (f(x)) | (searrow) | min | (nearrow) | (varnothing) | (nearrow) | max | (searrow) |
Функция возрастает при (xin(-2;1)cup(1;2))
Функция убывает при (xin(-infty;-2)cup(2;+infty))
Точка максимума (x=2; y_{max}=f(2)=frac{2^3-4}{(2-1)^3}=4)
Точка минимума (x=-2; y_{min}=f(-2)=frac{(-2)^3-4}{(-2-1)^3}=frac{-12}{-27}=frac49)
5) Вторая производная: begin{gather*} f»(x)=left(frac{-3(x^2-4)}{(x-1)^4}right)’=-3left(frac{2x(x-1)^4-(x^2-4)cdot 4(x-1)^3}{(x-1)^8}right)=\ =-3left(frac{2x(x-1)-4(x^2-4)}{(x-1)^5}right)=-3left(frac{2x^2-2x-4x^2+16}{(x-1)^5}right)=\ =-3left(frac{-2x^2-2x+16}{(x-1)^5}right)=frac{6(x^2+x-8)}{(x-1)^5}=frac{6(x-x_1)(x-x_2)}{(x-1)^5}\ D=1^2-4cdot (-8)=33, x_{1,2}=frac{-1pm sqrt{33}}{2}= left[ begin{array}{l} approx -3,37\ approx 2,37 end{array} right.\ f»(x)=0, text{при} x=x_{1,2} end{gather*} Критические точки 2-го порядка: (x=left{1;frac{-1pm sqrt{33}}{2}right})
| (x) | ((-infty;x_1)) | (x_1) | ((x_1;1)) | 1 | ((1;x_2)) | (x_2) | ((x_2;+infty)) |
| (f»(x)) | <0 | 0 | >0 | (varnothing) | <0 | 0 | >0 |
| (f(x)) | (cap) | перегиб | (cup) | (varnothing) | (cap) | перегиб | (cup) |
Функция выпуклая вверх при (xin(-infty;x_1)cup(1;x_2))
Функция выпуклая вниз при (xin(x_1;1)cup (x_2;++infty))
Точки перегиба: $$ begin{cases} x=frac{-1-sqrt{33}}{2}approx -3,37\ yapprox 0,51 end{cases}, begin{cases} x=frac{-1+sqrt{33}}{2}approx 2,37\ yapprox 3,62 end{cases} $$
6) Точки пересечения с осями
Пересечение с OY: (x=0, y=frac{0^3-4}{(0-1)^3}=4)
Пересечение с осью OX:
(frac{x^3-4}{(x-1)^3}=0Rightarrow x=sqrt[3]{4}, y=0)
7) График
Чтобы узнать количество корней уравнения (frac{x^3-4}{(x-1)^3}=a), нужно снизу вверх двигать горизонталь (y=a) и считать количество точек её пересечения с графиком функции.
Последовательно, получаем:
(altfrac{12}{27}) — один корень
(a=frac49) – два корня
(frac49lt alt 1) — три корня
(a=1) – два корня
(1lt alt 4) – три корня
(a=4) — два корня
(agt 4) — один корень
Ответ:
(altfrac49cup agt 4), один корень
(a=left{frac49;1;4right}), два корня
(frac{12}{27}lt 1lt 1cup 1lt alt 4), три корня
Пример 4*. Постройте график функции (y=sin^4x+cos^4x), используя правила преобразования тригонометрических функций и с помощью стандартной процедуры исследования функции
1) Область определения (xinmathbb{R})
2) Четность $$ f(-x)=sin^4(-x)+cos^4(-x)=sin^4x+cos^4x=f(x) $$ Функция четная.
Чтобы найти период, преобразуем тригонометрическое выражение, применяя формулы понижения степени (см. §15 данного справочника): begin{gather*} sin^4x+cos^4x=left(frac{1-cos2x}{2}right)^2+left(frac{1+cos2x}{2}right)^2=\ =frac14(1-2cos2x+cos^2 2x+1+2cos2x+cos^2 2x)=frac{1+cos^2 2x}{2}=\ =frac12left(1+frac{1+cos4x}{2}right)=frac{3+cos4x}{4} end{gather*} Функция периодическая с периодом (T=frac{2pi}{4}=frac pi 2)
Исходя из полученного выражения и применяя правила преобразования графиков тригонометрических функций (см. §8 данного справочника), можно сразу получить результат. $$ y=frac{3+cos4x}{4}=frac34+frac14 cos4x $$ Цепочка преобразований: $$ x xrightarrow1 4xxrightarrow2 cos4x xrightarrow3 frac14xrightarrow4 frac34+frac14 cos4x $$ Пошагово получаем:
1. Умножение аргумента на 4 приводит к уменьшению периода в 4 раза (T=fracpi 2)
2. Косинус – функция четная, при (x=0, cos4x=1), остальные единицы будут через период: (x=frac{pi k}{2}, cos4x=1). Соответственно: (x=fracpi 4+frac{pi k}{2}0 ,cos4x=-1).
Нули функции: (x=fracpi 8+frac{pi k}{4}, cos4x=0).
3. Умножение на (frac14) уменьшает амплитуду косинусоиды в 4 раза: (-frac14leqfrac14 cos4xleq frac14)
4. Прибавление (frac34) перемещает график на (frac34) вверх: (frac12leqfrac34+frac14 cos4xleq 1)
Получаем график:
Продолжим стандартное исследование функции.
3) Асимптоты
1. Вертикальных асимптот нет, т.к. нет точек разрыва 2-го рода.
2. Горизонтальных асимптот нет, т.к. нет пределов на бесконечности.
3. Наклонных асимптот нет, т.к. на бесконечности отношение ограниченной тригонометрической функции к бесконечному x дает (k=0).
4) Первая производная:
Исследуем промежуток, равный одному периоду (T=fracpi 2, 0leq xleqfracpi 2) begin{gather*} f'(x)=(sin^4 x+cos^4 x)’=left(frac{3+cos4x}{4}right)’=0-frac14cdot 4cdot sin4x=-sin4x\ sin4x=0Rightarrow 4x=pi kRightarrow x=frac{pi k}{4} end{gather*} Критические точки: (x=frac{pi k}{4}). На периоде (T=fracpi 2) получаем три точки (x=left{0;fracpi 4;fracpi 2right})
| (x) | 0 | (left(0;fracpi 4right)) | (fracpi 4) | (left(fracpi 4;fracpi 2right)) | (fracpi 2) |
| (f'(x)) | 0 | <0 | 0 | >0 | 0 |
| (f(x)) | 1 max |
(searrow) | (frac12) min |
(nearrow) | 1 max |
Функция убывает при (xinleft(frac{pi k}{2};fracpi 4+frac{pi k}{2}right))
Функция возрастает при (xinleft(fracpi 4+frac{pi k}{2};fracpi 2+frac{pi k}{2}right))
Точки минимума (x=fracpi 4+frac{pi k}{2}; y_{min}=frac12)
Точки максимума (x=frac{pi k}{2}; y_{max}=1)
5) Вторая производная: begin{gather*} f»(x)=(-sin4x)’=-4cos4x\ cos4x=0Rightarrow 4x=fracpi 2+pi kRightarrow x=fracpi 8+frac{pi k}{4} end{gather*} Критические точки 2-го порядка: (x=fracpi 8+frac{pi k}{4}).
На периоде (T=fracpi 2) получаем две точки (x=left{fracpi 8;frac{3pi}{8}right})
| (x) | (left(0;fracpi 8right)) | (fracpi  |
(left(fracpi 8;frac{3pi}{8}right)) | (frac{3pi}{8}) | (left(frac{3pi}{8};fracpi 2right)) |
| (f»(x)) | <0 | 0 | >0 | 0 | <0 |
| (f(x)) | (cap) | перегиб | (cup) | перегиб | (cap) |
Функция выпуклая вниз при (xinleft(fracpi 8+frac{pi k}{2};frac{3pi}{8}+frac{pi k}{2}right))
Функция выпуклая вверх при (xinleft(-fracpi 8+frac{pi k}{2};fracpi 8+frac{pi k}{2}right))
Точки перегиба: ( x=fracpi 8+frac{pi k}{4}, y=frac{3+cos4cdot left(fracpi 8+frac{pi k}{4}right)}{4}=frac{3+0}{4}=frac34 )
6) Точки пересечения с осями
Пересечение с OY: (x=0, y_{max}=1)
Пересечение с осью OX: т.к. функция ограничена (frac12leq yleq 1), пересечений с OX нет.
7) График
График тот же, что и полученный с помощью правил преобразований графиков тригонометрических функций. Добавились только точки перегиба.


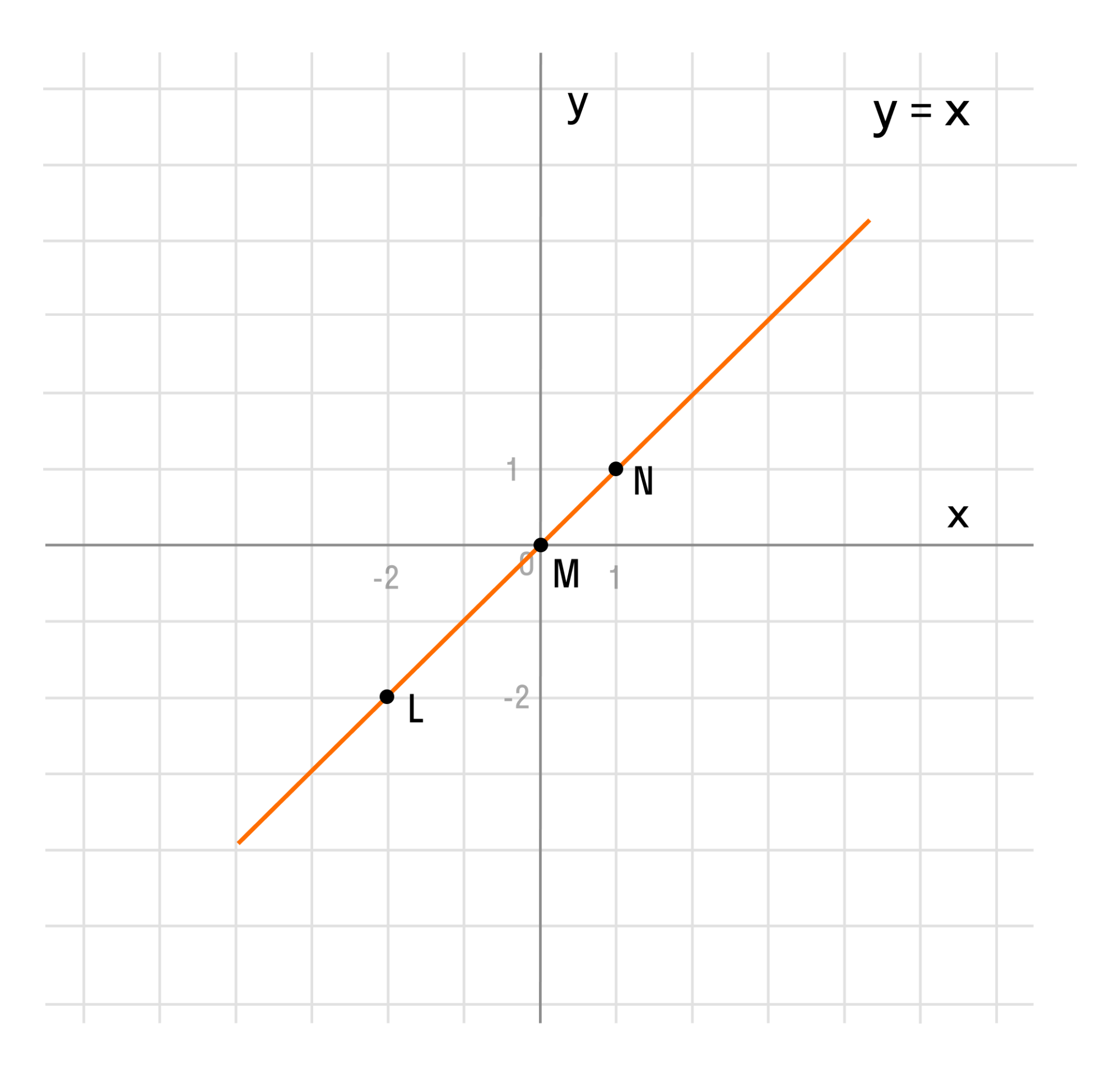
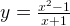
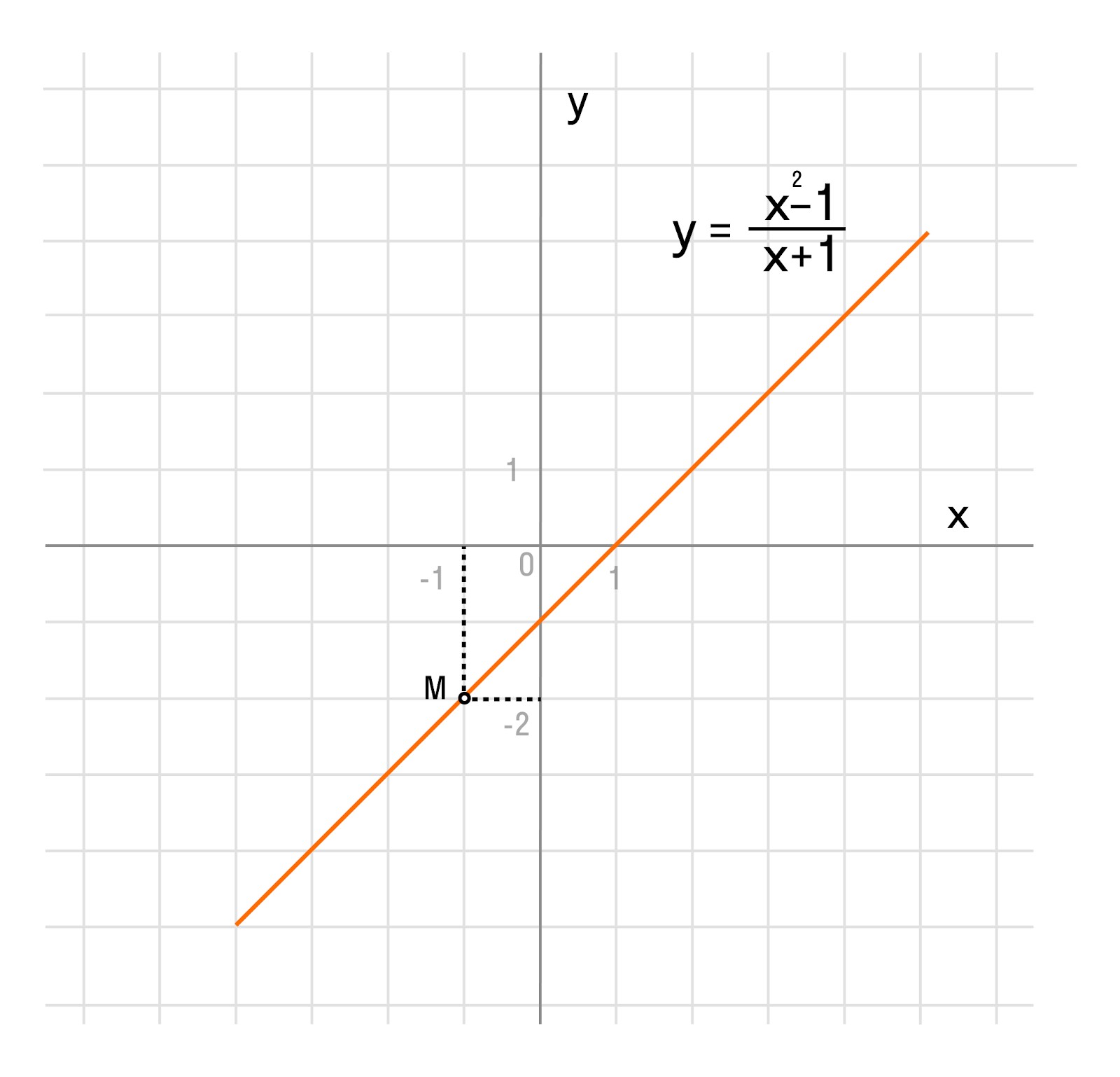
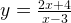
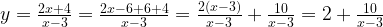
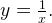
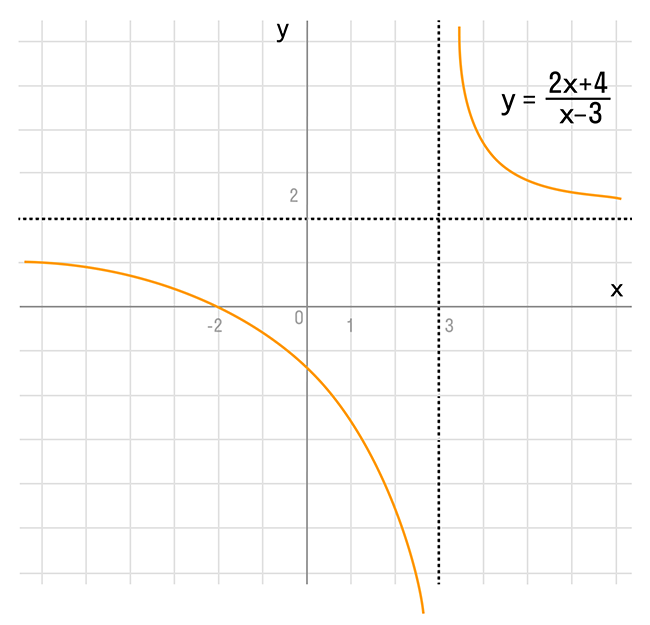
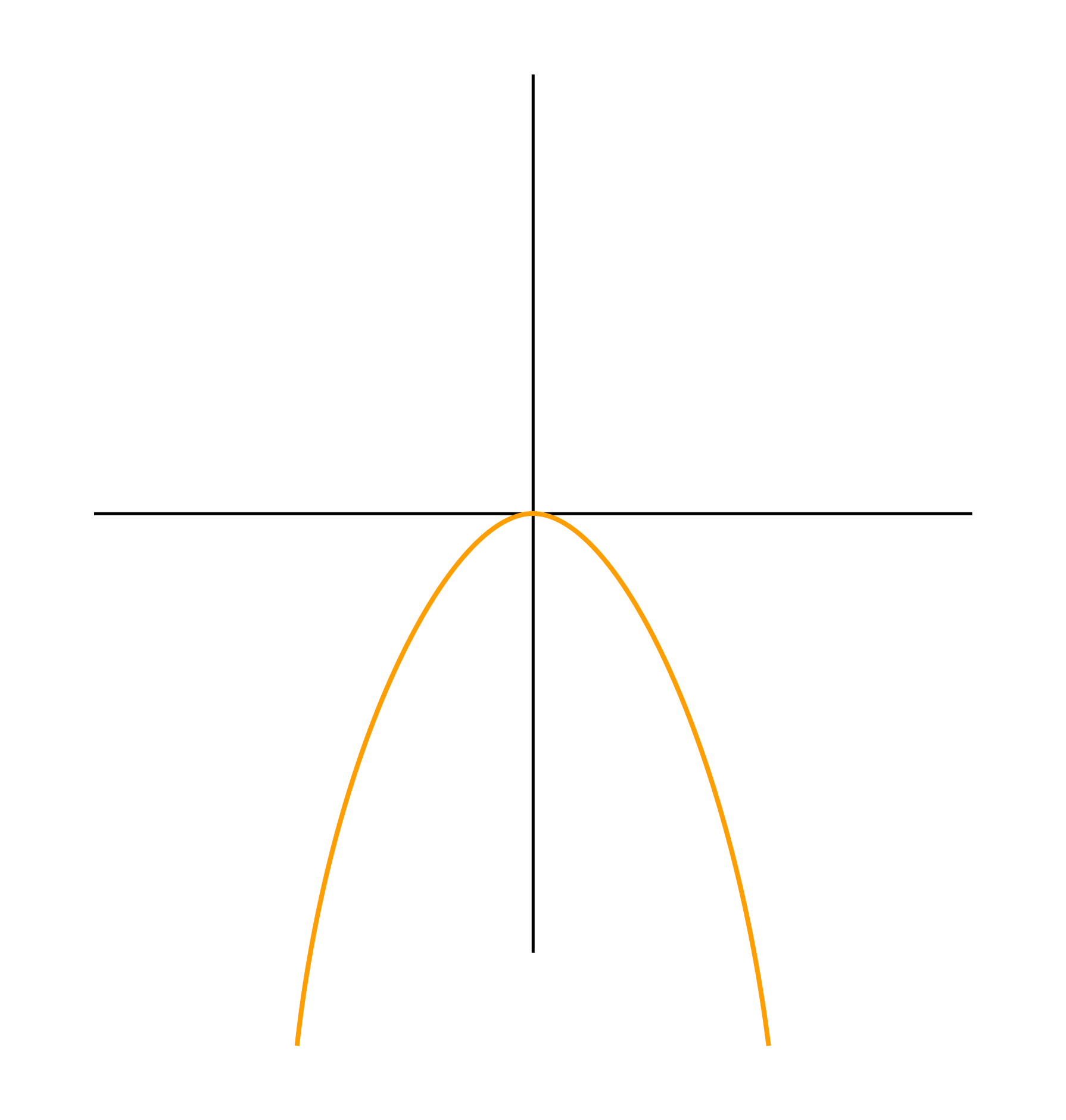
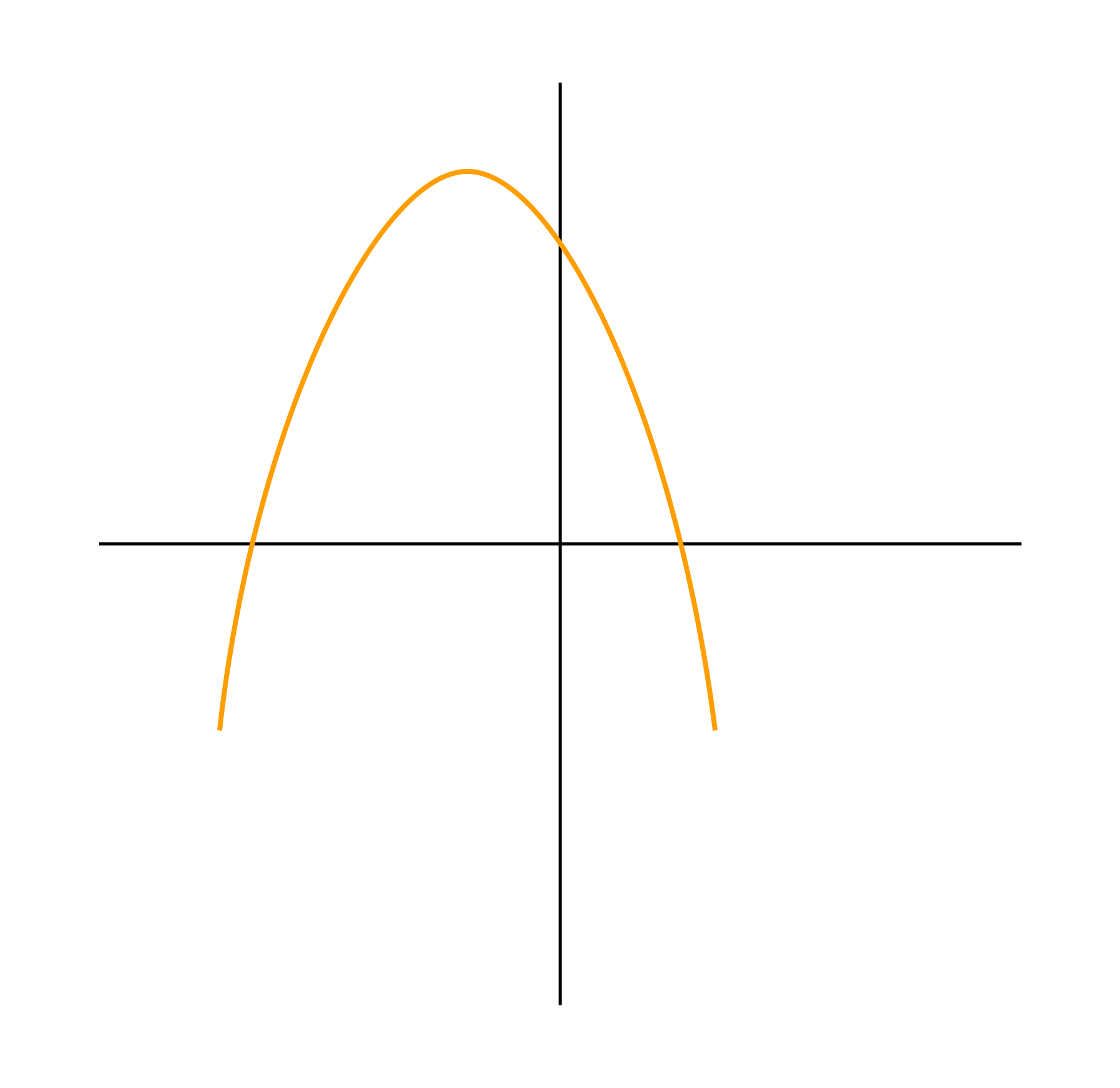
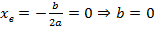
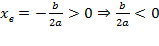 , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.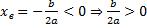 , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.