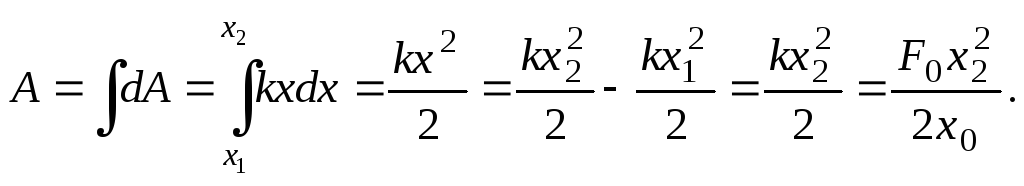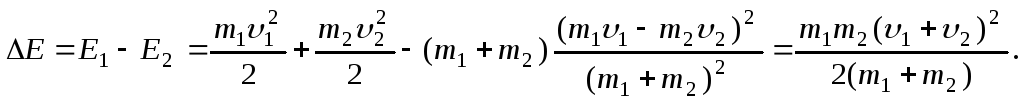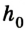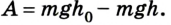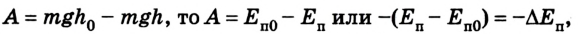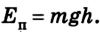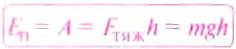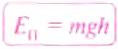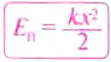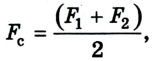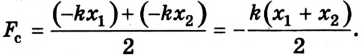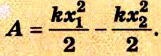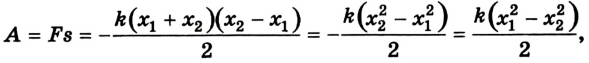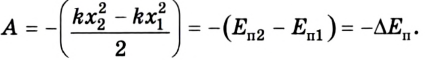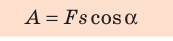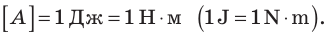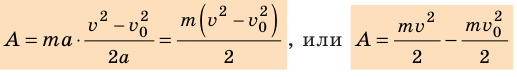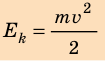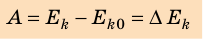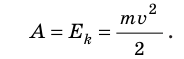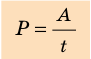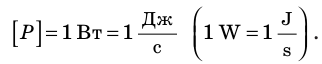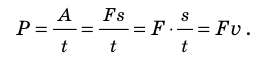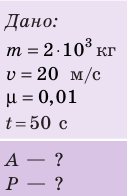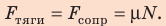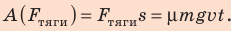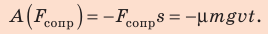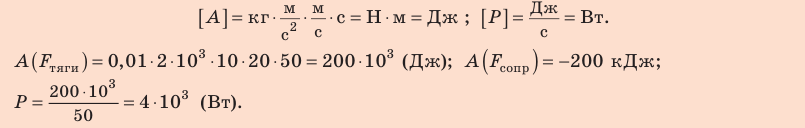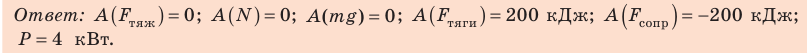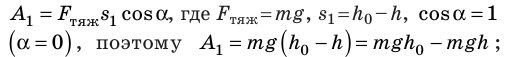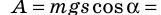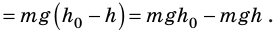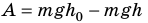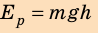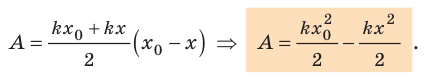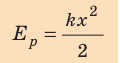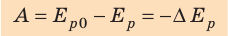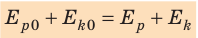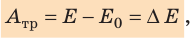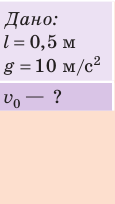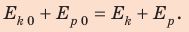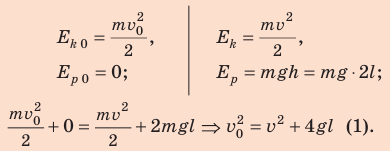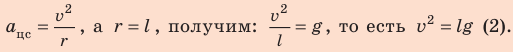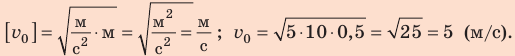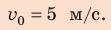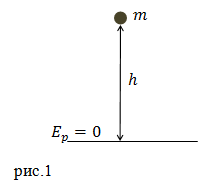Между
потенциальной энергией системы
взаимодействующих тел и консервативной
силой, обусловливающей наличие этой
энергии, существует вполне определенная
связь. Установим эту связь.
1.
Если в каждой точке пространства на
тело действует консервативная сила, то
говорят, что оно находится в потенциальном
поле.
2.
При изменении положения тела в этом
поле потенциальная энергия тела
изменяется, при этом консервативная
сила совершает вполне определенную
работу. Выразим эту работу обычным
образом.
Будем
полагать, что тело переместилось в
произвольном направлении
на бесконечно малое расстояние
(рис.25). Тогда
, (19.1)
где
— проекция вектора силы на направление
.
Но(19.2)
П
правые части выражений (19.1) и (19.2),
получим:,
откуда.
(19.3)
есть
производная потенциальной энергии по
направлению
;
эта величина показывает,насколько
быстро изменяется потенциальная энергия
вдоль этого направления.
Таким
образом, проекция
силы на
произвольное направление равна по
величине и противоположна по знаку
производной
от потенциальной энергии по этому
направлению.
Выясним
смысл знака «минус». Если в направлении
потенциальная энергия возрастает (
>
0), то согласно (19.3)<
0. Это значит, что направление силыобразует с направлением
тупой угол,
следовательно, составляющая этой силы,
действующая вдоль
,
противоположна направлению.
И наоборот, если< 0, то проекция
> 0, угол между силой
и направлением
острый,
со-
ставляющая
этой силы, действующая вдоль
,
совпадает с направлением.
3.
В общем случае потенциальная энергия
может изменяться не только в направлении
,
но и в любом другом направлении. Можно
рассматривать, например, изменениявдоль осей
,
декартовой системы координат.
Тогда (19.4)
(значок
означает, что беретсячастная
производная).
Зная
проекции силы
легко найти вектор силы:
. (19.5)
Учитывая
(19.4) будем иметь:
. (19.6)
Вектор,
стоящий в правой части соотношения
(19.6), называется градиентом
величины
и обозначается
.
Следовательно,
=
—. (19.7)
Консервативная
сила, действующая на тело, равна по
величине и противоположна по направлению
градиенту потенциальной энергии этого
тела. Градиент потенциальной энергии
– это вектор, указывающий направление
быстрейшего возрастания потенциальной
энергии и численно равный изменению
энергии, приходящемуся на единицу длины
этого направления.
При
перемещении тела в направлении
действия
консервативной силы
совершаетсямаксимальная
работа (так как
=1).
Но.
Следовательно, направление силыуказывает направление быстрейшегоуменьшения
потенциальной энергии.
20 Графическое представление потенциальной
ЭНЕРГИИ
1.
Потенциальная энергия является функцией
координат.
В некоторых простейших случаях она
зависит только от одной координаты
(например, в случае поднятого над Землей
тела
зависит только от высоты
).
Зависимость потенциальной энергии
системы от той или иной координаты может
быть представленаграфически.
График,
изображающий зависимость потенциальной
энергии от соответствующей координаты,
называют потенциальной
кривой.
Проанализируем
одну из возможных потенциальных кривых
(рис.26). Кривая
(
),
изображенная на рисунке, показывает,
как изменяется потенциальная энергия
системы частиц, если одна из частиц
перемещается вдоль оси,
а все остальные остаются на своих местах.
Каждая точка графика дает возможность
определитьсистемы, соответствующую координате
частицы.
2.
По наклону потенциальной кривой можно
судить о величине и направлении силы,
действующей на частицу вдоль
соответствующего 
Величина и знак проекции этой силы на
рассматриваемое направление определяется
величиной и знаком тангенса угла наклона
касательной к кривойв соответствующих точках; в нашем
случае,
(20.1)
так
как .
Таким
образом, чем
круче идет
потенциальная кривая, тем больше
сила,
действующая на частицу вдоль
соответствующего направления. На
восходящих участках потенциальной
кривой тангенсы углов наклона касательных
положительны, следовательно, проекция
силы отрицательна.
Это значит, что направление силы,
действующей вдоль
данной оси, противоположно
направлению этой оси, сила препятствует
удалению частицы из системы (рис.26, точка
).
В
точках же, соответствующих нисходящим
участкам потенциальной кривой, проекции
силы
положительны,
сила способствует дви-жению частицы
вдоль данного направления (точка
).
В точках, в которых=0,
сила на частицу не действует (точка).
3.
Если же при удалении одной из частиц (в
любом направлении) потенциальная энергия
системы резко возрастает
(потенциальная кривая «взмывает» вверх),
то говорят о существовании потенциального
барьера.
Говорят о высоте
барьера и
его ширине в соответствую-
щ
местах. Так, если частица находится в
точке с координатой(рис.26), то ее потенциальная энергия
равна,
высота потенциального барьера для нее,
ширина барьера.
Если потенциальный барьер встречается
на пути частицы при ее движении, как в
положительном, так и в отрицательном
направлении выбранной оси, то говорят,
что частица находится впотенциальной
яме. Форма
и глубина потенциальной ямы зависит от
природы сил взаимодействия и конфигурации
системы.
4.
Приведем некоторые примеры. На рис.27
изображена потенци-
альная
кривая тела, поднятого над Землей. Как
известно, потенциальная энергия такого
тела зависит только от одной координаты
– высоты
:
=P
.
Проекция
силы тяжести на ось
равна
.
З
«минус» означает, что направление силы
тяжести противоположно направлению
оси.
На рис.28 изображена потенциальная кривая
тела, скрепленного с пружиной и
совершающего колебания. Как видно из
рисунка, такое тело находится в
потенциальной яме с симметричными
стенками. Потенциальная энергия этого
тела и проекция силы, действующей на
него, равны соответственно:
,
.
Кривая,
изображенная на рис.29, характерна для
взаимодействия атомов и молекул в
твердом теле. Особенностью этой кривой
является то, что она асимметрична; один
край ее крутой, другой – пологий.
Наконец,
кривая на рис.30 характеризует, в первом
приближении, потенциальную энергию
свободных электронов в металле. Стенки
этой ямы почти вертикальны. Это значит,
что сила, действующая на электроны на
границе металла, весьма велика.
Г
горизонтальное дно ямы означает, что
на электроны внутри металла сила не
действует.
ПРИМЕРЫ
РЕШЕНИЯ ЗАДАЧ
Пример
1.
Определить
работу по сжатию пружины железнодорожного
вагона на 5 см,
если под
действием
силы
пружина сжимается на
Решение.
Пренебрегая
массой пружины, можно считать, что при
ее сжатии действует только переменная
сила давления, равная по величине упругой
силе, определяемой по закону Гука
.
Работу этой силы при сжатии пружины на
5см
надо определить. Считая на малом
перемещении
силу
постоянной, определим элементарную
работу как
.
Здесь
коэффициент жесткости пружины равен
.
Всю
работу найдем взяв интеграл от
в пределах отх1
= 0 до
х2
= 5
см.
После вычислений
будем иметь
.
Пример
2. Самолет
массы m=3
т
для взлета должен иметь скорость
=360км/ч и
длину разбега S=600
м.
Какова должна быть минимальная мощность
мотора, необходимая для взлета самолета?
Коэффициент трения k
колес о землю равен 0,2. Движение при
разгоне самолета считать равноускоренным.
Решение.
В задаче
требуется определить мгновенную
мощность мотора в
момент взлета
самолета. Она и будет являться той
минимальной мощностью, при которой
самолет может еще набрать скорость,
необходимую для взлета.
.
Силу
тяги
определим из уравнения (второй закон
динамики)
Ускорение
найдем из уравнения равнопеременного
движения
;
С учетом сделанных
замечаний минимальная мощность равна
.
Пример
3. Скорость
реактивного самолета на некотором
участке меняется с расстоянием по закону
.
Найти работу за промежуток времени (,
если масса самолетаm.
В момент времени
скорость равна
Решение.
Примем, что
работа равна разности кинетических
энергий в моменты времени
и
,
т.е..
Необходимо определить закон изменения
скорости со временем. Ускорение самолетаОткуда
.
После интегрирования и потенцирования
последнего выражения получим, что
скорость в момент времениравна
Таким образом
работа, за заданный промежуток времени,
равна
Пример
4. Тело массой
m
под действием
постоянной силы ветра движется
прямолинейно, причем зависимость
пройденного пути от времени меняется
по закону
.
Найти работу силы ветра за промежуток
времени от 0 доt.
Решение.
Работа силы
ветра при малом перемещении тела равна
,
где перемещение найдем как производную
от пути по времени, т.е.
Сила по второму закону динамики равна
Полная
работа за промежуток времени от 0 до t
равна
интегралу от
Пример
5. Шар массой
движется со скоростью
навстречу
шару массой,
движущемуся со скоростью
.
Найти величину и объяснить причину
изменения кинетической энергии системы
шаров после неупругого центрального
удара.
Решение.
Энергия
системы шаров до удара
После
неупругого удара шары будут двигаться
с одинаковой скоростью u,
которую найдем, применяя закон сохранения
импульса
.
Откуда
Энергия системы
шаров после удара
.
Убыль кинетической
энергии после удара
Изменение
кинетической энергии расходуется на
деформацию и в конечном счете на
нагревание шаров:
Пример
6. Автомобиль
массой
,
движущийся по горизонтальному участку
пути со скоростью,
развивает мощность, равную.
Какую мощность должен развивать
автомобиль при движении его в гору с
уклономс той же скоростью?
Определить
крутизну спуска (угол наклона), по
которому автомобиль будет идти со
скоростью 30 км/час,
при выключенном моторе.
Решение.
1) Мощность
автомобиля при движении в гору будет
определяться силой тяги и скоростью
движения
.
Сила
трения определяется как
,
где сила нормального давления на
наклонной плоскости.
Если считать коэффициент трения
одинаковым на всем пути движения, то на
горизонтальном участке он равен.
Сила трения может быть найдена из
соотношения (при равномерном горизонтальном
движении),
т.е.и
.
Тогда сила трения на наклонной плоскости
Скатывающая
сила равна
.
С учетом сделанных замечаний мощность
автомобиля, движущегося в гору будет
равна
Подставим данные
задачи
2)
При движении
под гору при выключенном двигателе сила
тяги равна нулю. Действуют только
скатывающая сила
и сила трения
С учетом их направления
—
,
откуда
.
Таким
образом, крутизна спуска равна
.
Пример
7. Тяжелый
шарик соскальзывает без трения по
наклонному желобу, образующему ”мертвую
петлю” радиуса R.
С какой высоты шарик должен начать
движение, чтобы не оторваться от желоба
в верхней точке траектории?
Решение.
Дана задача
о неравномерно переменном движении
материальной точки по окружности. Причем
в процессе движения изменяется положение
тела по высоте. Такие задачи решаются
с применением закона сохранения энергии
и составлением уравнения по второму
закону динамики для направления нормали.
Так как для замкнутой системы энергия
остается неизменной, то запишем это в
виде
.
Примем
за начальное положение шарика начало
движения, за конечное – положение в
верхней точке траектории. Уровень
отсчета высоты установим от поверхности
стола.
Энергия
шарика в первом положении
,
во втором положении.
Следовательно,
откуда
. (1)
Для
определения h
необходимо знать скорость шарика в
верхней точке. При этом учтем, что в
верхней точке петли на шарик в общем
случае действуют вниз две силы – сила
тяжести Р и
сила реакции со стороны опоры N.
Под действием этих сил шарик движется
по окружности, т.е.
При
спуске с достаточно большой высоты
шарик приобретает такую скорость, что
в каждой точке петли давит на желоб с
некоторой силой
.
По третьему закону Ньютона желоб
действует на шарик с такой же по величине
силойN
в противоположную сторону и отжимает
его на дугу окружности радиуса R.
По
мере уменьшения начальной высоты
скорость шарика уменьшается и при
некотором значении h
становится такой, что он пролетает
верхнюю точку петли, лишь касаясь желоба.
Для такого предельного случая N
= 0 и уравнение
второго закона динамики примет вид
или
откуда
(2)
Подставив
(2) в (1) и решая последнее уравнение
относительно h,
получим
ВОПРОСЫ
ДЛЯ САМОПРОВЕРКИ.
1.
Что называется энергией? Что называется
кинетической энергией? Что называется
потенциальной энергией?
2.
Что такое работа? Как вычисляется работа
постоянной и переменной силы?
3. Что такое
мощность?
4.
Какова связь между механической работой
и кинетической энергией?
5.
Докажите, что сила тяжести является
консервативной силой.
6.
Какова связь между работой консервативных
сил и потенциальной энергией?
7.Что
такое нулевой уровень потенциальной
энергии? Как он выбирается?
8.
Какова связь между потенциальной
энергией тела и консервативной силой,
действующей на него?
9. Что такое
потенциальная яма и потенциальный
барьер?
ИСПОЛЬЗУЕМАЯ
ЛИТЕРАТУРА
Савельев
И. В. Курс общей физики: в 3 т.; учебное
пособие для вузов. т.1: Механика.
Молекулярная физика. /И.В. Савельев.-4-е
изд. стер.-СПб.: Лань, 2005.
Зисман
Г. А. Курс общей физики. Т.1 /Г.А. Зисман,
О.М.Тодес.– М.:Наука,1972.
Детлаф
А. А. Курс физики: учебное пособие для
втузов. /А.А. Детлаф, Б.М. Яворский.-4-е
изд., испр.- М.: Высш.шк.,2002.- 718 с.
Трофимова
Т.И. Курс физики: учебное пособие для
вузов. /Т.И.Трофимова.- 7-е изд., стер.- М.:
Высш. шк., 2001.- 541 с.
Чертов
А.Г. Задачник по физике: учебное пособие
для втузов./А.Г.Чертов, А.А.Воробьев.- 8-е
изд., перераб. и доп.- М.: Физматлит, 2006.-
640 с.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение потенциальной энергии
Энергия, говоря простым языком, это возможность что-либо сделать, возможность совершить работу. То есть, если какое-либо тело может совершить какую-либо работу, то про это тело можно сказать, что оно обладает энергией. По сути, энергия — это мера различных форм движения и взаимодействия материи, а её изменение происходит при совершении некоторой работы. Таким образом, совершённая работа всегда равна изменению какой-либо энергии. А значит, рассматривая вопрос о совершённой телом работе, мы неизбежно приходим к изменению какого-либо вида энергии. Вспомним также и тот факт, что работа совершается только в том случае, когда тело под действием некоторой силы движется, и при этом сама работа определяется как скалярное произведение вектора этой силы и вектора перемещения, то есть А = F*s*cosa, где а — угол между вектором силы и вектором перемещения. Это нам пригодится в дальнейшем для вывода формул различных видов энергии.
Энергию, связанную с взаимодействием тел, называют ПОТЕНЦИАЛЬНОЙ ЭНЕРГИЕЙ. Иначе говоря, если тело за счёт взаимодействия с другим телом может совершить некоторую работу, то оно будет обладать потенциальной энергией, и при совершении работы будет происходить изменение этой энергии. Обозначают механическую потенциальную энергию чаще всего — Еп.
Виды потенциальной энергии
Существуют различные виды потенциальной энергии. К примеру, любое тело на Земле находится в гравитационном взаимодействии с Землёй, а значит обладает потенциальной энергией гравитационного взаимодействия. И ещё пример — витки растянутой или сжатой пружины находятся в упругом взаимодействии друг с другом, а значит сжатая или растянутая пружина будет обладать потенциальной энергией упругого взаимодействия.
Далее мы рассмотрим только виды механической потенциальной энергии и формулы, по которым их можно рассчитать. Но в дальнейшем вы узнаете и о других видах потенциальной энергии — к примеру, о потенциальной энергии электрического взаимодействия заряженных тел, о потенциальной энергии взаимодействия электрона с атомным ядром.

Знакомьтесь: наш мир. Физика всего на свете.
Книга адресована школьникам старших классов, студентам, преподавателям и учителям физики, а также всем тем, кто хочет понять, что происходит в мире вокруг нас, и воспитать в себе научный взгляд на все многообразие явлений природы. Каждый раздел книги представляет собой, по сути, набор физических задач, решая которые читатель укрепит свое понимание физических законов и научится применять их в практически интересных случаях.
Купить
Формулы потенциальной энергии
Перед тем как приступить к выводу формул потенциальной энергии, ещё раз вспомним, что совершённая телом или над телом работа равна изменению его энергии. При этом, если само тело совершает работу, то его энергия уменьшается, а если над телом совершают работу, то его энергия увеличивается. К примеру, если спортсмен поднимает штангу, то он сообщает ей потенциальную энергию гравитационного взаимодействия, а если он отпускает штангу и она падает, то потенциальная энергия гравитационного взаимодействия штанги с Землёй уменьшается. Также, если вы открываете дверь, растягивая пружину, то вы сообщаете пружине потенциальную энергию упругого взаимодействия, но если потом дверь закрывается, благодаря сжатию пружины в начальное состояние, то и энергия упругой деформации пружины уменьшается до нуля.
А) Чтобы вывести формулу потенциальной энергии гравитационного взаимодействия, рассмотрим, какую работу совершает тело, двигаясь под действием силы тяжести:
А = F*s = mg*s = mg*(h1
— h2) = mgh1
— mgh2
= Eп1
— Еп2, то есть, мы получили, что потенциальная энергия гравитационного взаимодействия тела с Землёй может быть вычислена по формуле: Еп = mgh.
Здесь важно отметить, что поверхность Земли принимается за начало отсчёта высоты, то есть для тела, находящегося на поверхности Земли Еп = 0, для тела, поднятого над Землёй Еп > 0, а для тела, находящегося в яме глубиной h, Еп < 0.
Отметим также и то, что в формуле работы отсутсвовал cosa. Это не случайно. Ведь если тело движется по сложной траектории, то, какой бы сложной она ни была, её можно разбить на множество вертикальных и горизонтальных участков. Но на горизонтальных участках работа силы тяжести будет равна нулю, так как угол между силой тяжести и перемещением будет прямым, а значит работа будет совершаться только на вертикальных участках траектории, для которых cosa = 1 или cosa = −1.
Тогда можно сделать ещё один важный вывод — работа силы тяжести не зависит от формы траектории, а только от расположения начальной и конечной точки. А это не случайность — это свойство любых сил, сообщающих телам потенциальную энергию. Такие силы называют потенциальными и сила тяжести — одна из них. К потенциальным силам относится и сила упругости.
Б) Чтобы вывести формулу потенциальной энергии упругой деформации, рассмотрим, какую работу нужно совершить, чтобы растянуть пружину, изменив её длину на х (х = l — l0):
А = –Fупр(ср.)*s,
Во-первых, знак минус в формуле стоит потому, что угол между силой упругости и перемещением свободного конца пружины равен 180 градусов и cosa = −1.
Во-вторых, возникающая при растяжении пружины сила упругости является переменной силой, в отличие от силы тяжести, поэтому в формуле работы стоит средняя сила упругости. При этом величина силы упругости, в соответствии с законом Гука, прямо пропорциональна изменению длины пружины, а значит её среднее значение можно определить так:
Fупр(ср.) = (Fупр(нач.) + Fупр(конеч.))/2
И так как Fупр(нач.) = 0, а Fупр(конеч.) = kх, то:
А = —kх*s/2
Но s = x, поэтому: А = —kx2/2 = 0 — kх2/2 = Еп1 — Еп2.
В итоге, мы получили формулу потенциальной энергии упругой деформации: Еп = kx2/2.
Методические советы учителям
1) Обязательно обратите внимание учащихся на связь энергии и работы.
2) Не давайте учащимся формулы потенциальной энергии без вывода.
3) Обратите внимание учащихся на то, что оба вида потенциальной энергии зависят от выбора начальной точки, то есть от системы координат.
4) При выводе формул потенциальной энергии обязательно поясните учащимся почему отсутствует cosa в формуле работы.
5) Отметьте, что и работа силы тяжести, и работа силы упругости не зависят от формы траектории и, следовательно равны нулю на замкнутой траектории — это общее и важное свойство всех потенциальных сил.
#ADVERTISING_INSERT#
Содержание:
Потенциальная энергия:
По определению потенциальная энергия — это энергия взаимодействия. Т. е. потенциальную энергию имеют все взаимодействующие тела. Для каждого вида механического взаимодействия можно рассчитать потенциальную энергию, учитывая особенности данного взаимодействия.
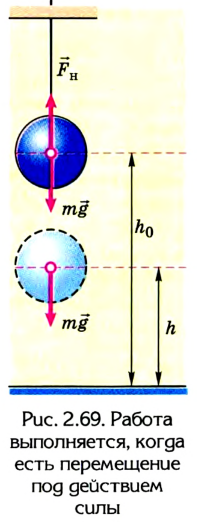
Самым распространенным в природе является гравитационное взаимодействие, проявлением которого является сила тяжести. При определенных условиях эта сила может выполнять работу.
Допустим, тело массой т подвешено над полом на высоте
Если нить перерезать, то тело начнет падать под действием силы тяжести.
По определению работа А = Fs cos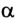
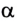
Если учесть, что 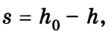
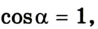
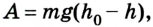
Поскольку работа равна изменению энергии, то можно считать, что выражение mgh определяет потенциальную энергию тела в поле силы тяжести Земли на высоте Л. Движение под действием силы тяжести может происходить по разным траекториям. Выясним, будет ли это влиять на значение работы.
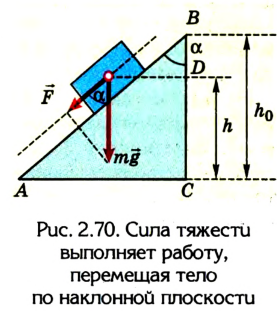
Дадим возможность телу свободно скользить без трения по наклонной плоскости под действием силы тяжести (рис. 2.70).
Если учитывать, что А = mgscos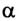
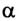
Из треугольника ABC ABcos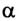
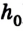
Тогда работа силы тяжести при скольжении тела без трения по наклонной плоскости будет равна А = mg(h — 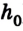
Следовательно, работа силы тяжести по перемещению тела по наклонной плоскости будет такой же, как и при его падении из точки В, расположенной на высоте 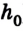
Таким образом, работа силы тяжести определяется положением точек начала и конца движения и не зависит от формы траектории.
В тех случаях, когда работа силы не зависит от формы траектории, а определяется начальным и конечным положением тела, пользуются понятием потенциальной энергии.
Если записать формулу для работы силы тяжести в виде
т. е. работа определяется изменением величины mgh, которая называется потенциальной энергией тела в поле силы тяжести:
Работа силы тяжести равна изменению потенциальной энергии тела с противоположным знаком. Это означает, что при падении тела, когда сила тяжести выполняет положительную работу, его потенциальная энергия уменьшается. И наоборот, при движении тела вверх, когда сила тяжести выполняет отрицательную работу, его потенциальная энергия увеличивается. Эта особенность характерна для всех случаев, когда работа силы не зависит от формы траектории.
Что такое потенциальная энергия
Потенциальная энергия (от латинского слова потенциал — возможность) — это энергия, которая определяется взаимным положением взаимодействующих тел или частей одного тела.
Поскольку любое тело и Земля притягивают друг друга, т. е. взаимодействуют, то потенциальная энергия тела, поднятого над Землей, будет зависеть от высоты подъёма h. Чем больше высота подъёма тела, тем больше его потенциальная энергия.
Опытами установлено, что потенциальная энергия тела зависит не только от высоты, на которую оно поднято, но и от массы тела. Если тела подняты на одинаковую высоту, то тело, у которого масса больше, будет иметь и ббльшую потенциальную энергию. Во время падения поднятого тела на поверхность Земли сила тяжести выполнила работу, соответствующую изменению потенциальной энергии тела со значения её на высоте И до значения на поверхности Земли. Если для удобства принять, что потенциальная энергия тела на поверхности Земли равна нулю, то потенциальная энергия поднятого тела будет равна выполненной во время падения работе:
Итак, потенциальную энергию тела, поднятого на некоторую высоту, будем определять по формуле:
где Еп — потенциальная энергия поднятого тела; m — масса тела; 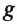
h — высота, на которую поднято тело.
Большой запас потенциальной энергии у воды горных или равнинных рек, поднятых плотинами. Падая с высоты вниз, вода выполняет работу: приводит в движение турбины гидроэлектростанций. В Украине на Днепре построено несколько гидроэлектростанций, в которых используют энергию воды для получения электроэнергии. На рисунке 174 изображено сечение такой станции. Вода с более высокого уровня падает вниз и вращает колесо гидротурбины. Вал турбины соединён с генератором электрического тока.
Потенциальной энергией обладает самолёт, летящий высоко в небе; дождевые капли в туче; молот копра при забивании свай. Открывая двери с пружиной, мы растягиваем её, преодолевая силу упругости, т. е. выполняем работу. Вследствие этого пружина приобретает потенциальную энергию. За счёт этой энергии пружина, сокращаясь, выполняет работу — закрывает двери. Потенциальную энергию пружин используют в часах, разнообразных заводных игрушках. В автомобилях, вагонах пружины амортизаторов и буферов, деформируясь, уменьшают толчки.
Потенциальная энергия пружины зависит от её удлинения (изменения длины при сжатии или растяжении) и жёсткости (зависит от конструкции пружины и упругости материала, из которого она изготовлена). Чем больше удлинение (деформация) пружины, и чем больше её жёсткость, тем большую потенциальную энергию она приобретает при деформации. Такая зависимость свойственна любому упруго деформированному телу.
Потенциальную энергию упругодеформированного тела определяют по формуле:
где 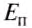
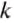
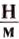
Но тела могут обладать энергией не только потому, что они находятся в определённом положении или деформируются, а и потому, что они находятся в движении.
Определение потенциальной энергии
В повседневной жизни можно обнаружить множество различных тел, при перемещении которых может выполняться работа. Так, выпавший из рук шарик начнет падать под действием силы притяжения, которая будет выполнять работу по перемещению шарика.
Сжатая пружина может поднять на определенную высоту груз. В этом случае сила упругости выполняет работу по перемещению груза.
Что такое энергия
Энергия — это физическая величина, показывающая, какая работа может быть выполнена при перемещении тела.
Можно привести еще много разных примеров из природы, из повседневной жизни, из техники, в которых речь идет о телах, находящихся в таком состоянии, что при определенных условиях может выполняться работа при их перемещении. О таких телах говорят, что они обладают энергией. При различных условиях результат выполнения работы может быть разным. Поэтому и энергия может иметь различные значения и может быть рассчитана.
Единицы энергии
Поскольку речь идет о возможности выполнения работы, то энергию целесообразно измерять в таких же единицах, что и работу. Поэтому единицей энергии есть 1 Дж.
Виды механической энергии
В физике выделяют два вида механической энергии: потенциальную и кинетическую. Если тело неподвижно, но па него действует определенная сила, то говорят, что оно обладает потенциальной энергией.
Потенциальной энергией обладает тело, поднятое над поверх-136 ностью Земли, сжатая пружина, сжатый газ, речная вода в водоеме и другие тела.
Как рассчитывают потенциальную энергию
Рассчитывают потенциальную энергию с учетом природы сил, действующих на эти тела. Проще всего рассчитать потенциальную энергию тела, поднятого над поверхностью Земли, поскольку сила, действующая на него, остается практически постоянной на протяжении всего времени его движения под действием этой силы.
Пусть тело массой 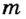
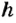
Следовательно, о таком теле можно сказать, что оно обладает потенциальной энергией
Потенциальная энергия тела, поднятого над поверхностью Земли, пропорциональна массе тела и его высоте над поверхностью Земли.
При расчете потенциальной энергии важно помнить, что высота 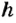
Потенциальная энергия упруго деформированного тела
Расчет работы силы упругости усложняется тем, что в ходе выполнения работы значение силы изменяется. Поскольку изменение силы упругости происходит линейно, то при расчетах работы используют среднее значение силы:
где 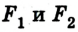
Учитывая, что 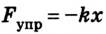
В случае, когда 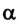
где 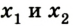
Для потенциальной энергии тела в поле силы тяжести можно записать:
Потенциальная энергия упруго деформированного тела зависит от его деформации.
Работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятой с противоположным знаком.
Как и в случае работы силы тяжести, работа силы упругости зависит не от формы траектории, а только от начальной и конечной деформации тела.
Механическая работа и кинетическая энергия
Чтобы шли механические часы, их нужно завести — закрутить пружину; раскручиваясь, пружина совершит работу. Поднявшись на вершину горы, лыжник создаст «запас работы» и в результате сможет скатиться вниз; при этом работу совершит сила тяжести. Самый простой способ разбить окно в горящем доме — бросить в окно камень. Если скорость движения камня достаточна, он разобьет окно — совершит работу. О теле или системе тел, которые могут совершить работу, говорят, что они обладают энергией.
Когда сила совершает механическую работу
Основная задача механики — определение механического состояния тела (координат тела и скорости его движения) в любой момент времени. Механическое состояние тела не изменяется само по себе — необходимо взаимодействие, то есть наличие силы. Когда тело перемещается (изменяет свое механическое состояние) под действием силы, говорят, что данная сила совершает механическую работу.
Механическая работа (работа силы) A — физическая величина, характеризующая изменение механического состояния тела и равная произведению модуля силы F, модуля перемещения s и косинуса угла a между вектором силы и вектором перемещения:
Единица работы в СИ — джоуль:
1 Дж равен механической работе, которую совершает сила 1 Н, перемещая тело на 1 м в направлении действия этой силы.
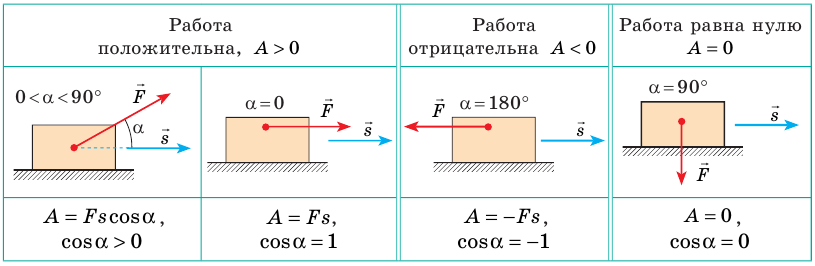
Работа силы — величина скалярная, однако она может быть положительной, отрицательной, равной нулю — в зависимости от того, куда направлена сила относительно направления движения тела (см. таблицу).
Геометрический смысл работы силы
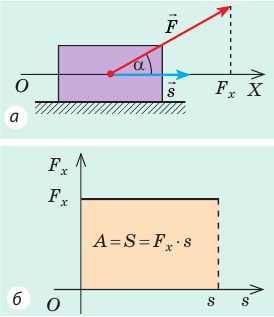
Рассмотрим силу, действующую под некоторым углом α к направлению движения тела. Найдем проекцию этой силы на направление перемещения тела, для чего ось ОХ направим в сторону движения тела (рис. 15.1, а). Из рисунка видим, что 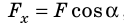
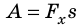
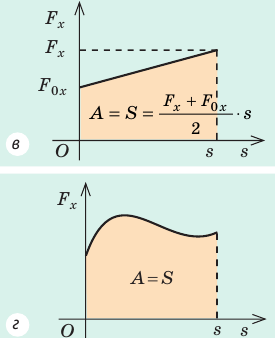
Построим график 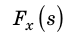
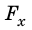
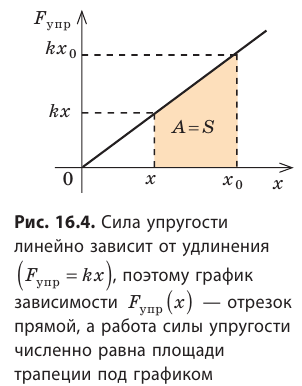
Рис. 15.1. Если направление оси ОХ совпадает с направлением движения тела, то работа A силы численно равна площади S фигуры под графиком зависимости
В этом состоит геометрический смысл работы силы: работа силы численно равна площади фигуры под графиком зависимости проекции силы от модуля перемещения. Это утверждение распространяется и на случаи, когда сила переменная (рис. 15.1, в, г).
Когда тело имеет кинетическую энергию
Рассмотрим тело массой m, которое под действием равнодействующей силы 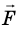
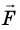
Величину 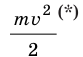
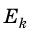
Кинетическая энергия — физическая величина, которая характеризует механическое состояние движущегося тела и равна половине произведения массы m тела на квадрат скорости v его движения:
Теорема о кинетической энергии: работа равнодействующей всех сил, которые действуют на тело, равна изменению кинетической энергии тела:
Если в начальный момент времени тело неподвижно (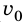
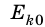
Кинетическая энергия тела, движущегося со скоростью v, равна работе, которую совершает сила, чтобы придать неподвижному телу данную скорость.
Мощность
До сих пор мы говорили о работе силы. Но любая сила характеризует действие определенного тела (или поля). Поэтому работу силы часто называют работой тела (работой поля), со стороны которого действует эта сила. На практике большое значение имеет не только выполненная работа, но и время, за которое эта работа была выполнена. Поэтому для характеристики механизмов, предназначенных для совершения работы, используют понятие мощности.
Мощность P (или N) — физическая величина, характеризующая скорость выполнения работы и равная отношению работы А к интервалу времени t, за который эта работа выполнена:
Единица мощности в СИ — ватт:
(Названа в честь Джеймса Ватта (1736–1819). Как единицу мощности он ввел лошадиную силу, которую иногда используют и сейчас: 1 л. с. = 746 Вт.)
Мощность, которую развивает транспортное средство, удобно определять через силу тяги и скорость движения. Если тело движется равномерно, а направление силы тяги совпадает с направлением перемещения, тяговую мощность двигателя можно вычислить по формуле:
Обратите внимание! Данная формула справедлива для любого движения: мощность, которую развивает двигатель в данный момент времени, равна произведению модуля силы тяги двигателя на модуль его мгновенной скорости: P = Fv (рис. 15.3).
Рис. 15.3. Когда для движения автомобиля требуется большая сила тяги, водитель переходит на меньшую скорость или нажимает на газ, увеличивая таким образом мощность двигателя
Чтобы определить механическую работу и мощность, нужно знать силу, действующую на тело, перемещение тела и время его движения. Поэтому обычно решение задач на определение работы и мощности сводится к решению задач по кинематике и динамике.
Пример №1
Автомобиль массой 2 т движется равномерно со скоростью 20 м/с по горизонтальному участку дороги. Какие силы действуют на автомобиль? Найдите работу каждой силы и тяговую мощность двигателя автомобиля, если коэффициент сопротивления движению равен 0,01, а время движения — 50 с.
Решение:
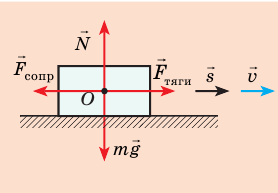
Выполним пояснительный рисунок, на котором укажем силы, действующие на автомобиль: силу тяжести 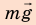
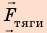
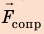
Чтобы определить работу каждой силы, нужно найти::
- угол между направлением этой силы и направлением перемещения;
- модуль силы и модуль перемещения.
1. Автомобиль движется равномерно, поэтому действующие на него силы скомпенсированы: — сила тяжести уравновешена силой нормальной реакции опоры: N = mg; — сила тяги уравновешена силой сопротивления движению:
2. Перемещение автомобиля можно найти по формуле: s = vt .
3. Сила тяжести и сила нормальной реакции опоры перпендикулярны направлению движения автомобиля (α = 90°, cosα = 0). Следовательно, работа этих сил равна нулю. Сила тяги направлена в сторону движения тела: α = 0, cosα = 1, поэтому:
Сила сопротивления противоположна движению: α = 180°, cosα = −1, поэтому:
4. Тяговую мощность двигателя автомобиля определим по формуле 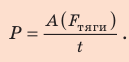
Выводы:
Потенциальная энергия и закон сохранения механической энергии
Поднятый молот не обладает кинетической энергией, так как его скорость равна нулю. Но если молот отпустить, он совершит работу (расплющит металл). Натянутая тетива лука не имеет кинетической энергии, но, выпрямляясь, она придаст скорость стреле, а значит, совершит работу. И деформированное тело, и тело, поднятое над поверхностью Земли, способны совершить работу, то есть обладают энергией. Что это за энергия и как ее рассчитать?
Когда тело обладает потенциальной энергией
Механическая энергия E — физическая величина, характеризующая способность тела (системы тел) совершить работу.
Единица энергии (как и работы) в СИ — джоуль [E] = 1 Дж (J).
Любое движущееся тело может совершить работу, поскольку оно обладает кинетической энергией, или «живой силой», как ее называли раньше. Есть еще один вид механической энергии — ее называли «мертвая сила». Это — потенциальная энергия (от лат. potentia — сила, возможность), — энергия, которую имеет тело в результате взаимодействия с другими телами.
Потенциальная энергия — энергия, которой обладает тело вследствие взаимодействия с другими телами или вследствие взаимодействия частей тела.
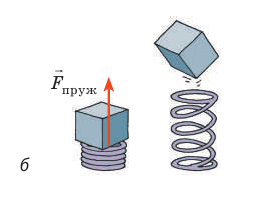
Рис. 16.1. И девочка в результате взаимодействия с Землей (а), и сжатая пружина в результате взаимодействия ее витков (б) обладают потенциальной энергией
Девочка на вершине горки (рис. 16.1, а) обладает потенциальной энергией, поскольку в результате взаимодействия с Землей может начать движение и сила тяжести совершит работу. Но как вычислить эту работу, ведь горка неровная и в течение всего времени движения угол между направлением силы тяжести и направлением перемещения будет изменяться?
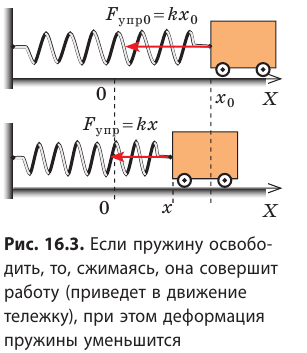
Сжатая пружина (рис. 16.1, б) тоже обладает потенциальной энергией: при распрямлении пружины сила упругости совершит работу — подбросит брусок. Но как вычислить эту работу, ведь во время действия пружины на брусок сила упругости непрерывно уменьшается?
Оказывается, все не так сложно. И сила тяжести, и сила упругости имеют одно «замечательное» свойство — работа этих сил не зависит от формы траектории. Силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным механическими состояниями тела (системы тел), называют потенциальными, или консервативными, силами (от лат. conservare — сохранять, охранять).
Потенциальная энергия поднятого тела
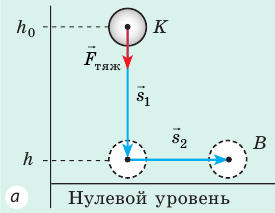
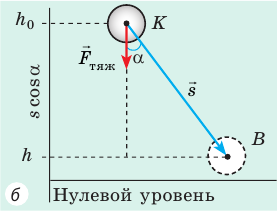
Докажем, что сила тяжести — консервативная сила. Для этого определим работу силы тяжести при движении тела из точки K в точку B по разным траекториям.
Случай 1. Пусть траектория движения тела — «ступенька» (рис. 16.2, а): сначала тело падает с некоторой высоты 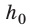
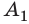
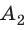
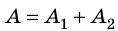
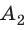
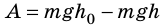
Случай 2. Пусть тело перемещается из точки K в точку В, скользя по наклонной плоскости (рис. 16.2, б). В этом случае работа силы тяжести равна:
Рис. 16.2. При перемещении тела с высоты 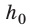
Тот же результат получим и для случаев перемещения тела по произвольной траектории. Следовательно, работа силы тяжести не зависит от траектории движения тела, то есть сила тяжести — консервативная сила. Величину mgh называют потенциальной энергией поднятого тела:
Потенциальная энергия поднятого тела зависит от высоты, на которой находится тело, то есть зависит от выбора нулевого уровня, — уровня, от которого будет отсчитываться высота. Нулевой уровень выбирают из соображений удобства. Так, находясь в комнате, за нулевой уровень целесообразно взять пол, определяя высоту горы — поверхность Мирового океана.
Обратите внимание! Изменение потенциальной энергии, а следовательно, и работа силы тяжести от выбора нулевого уровня не зависят.
- Заказать решение задач по физике
Потенциальная энергия упруго деформированного тела
Пусть имеется упруго деформированное тело — растянутая пружина. Определим работу, которую совершит сила упругости при уменьшении удлинения пружины от 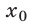
Таким образом, работа силы упругости определяется только начальным и конечным состояниями пружины, то есть сила упругости — консервативная сила. Величину 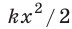
Работа силы упругости (как и силы тяжести) равна изменению потенциальной энергии тела, взятому с противоположным знаком:
Данное выражение — математическая запись теоремы о потенциальной энергии: работа всех консервативных сил, действующих на тело, равна изменению потенциальной энергии тела, взятому с противоположным знаком.
Состояние с меньшей потенциальной энергией является энергетически выгодным; любая замкнутая система стремится перейти в такое состояние, в котором ее потенциальная энергия минимальна, — в этом заключается принцип минимума потенциальной энергии. Действительно, камень, выпущенный из руки, никогда не полетит вверх — он будет падать, стремясь достичь состояния с наименьшей потенциальной энергией. Недеформированная пружина никогда не станет сама растягиваться или сжиматься, а деформированная пружина стремится перейти в недеформированное состояние.
Закон сохранения полной механической энергии
Как правило, тело или система тел обладают и потенциальной, и кинетической энергиями. Сумму кинетических и потенциальных энергий тел системы называют полной механической энергией системы тел: 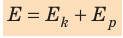
Рассмотрим замкнутую систему тел, взаимодействующих друг с другом только консервативными силами (силами тяготения или силами упругости). По теореме о потенциальной энергии работа A, совершаемая этими силами, равна: 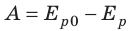
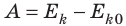
В замкнутой системе тел, взаимодействующих только консервативными силами, полная механическая энергия остается неизменной (сохраняется):
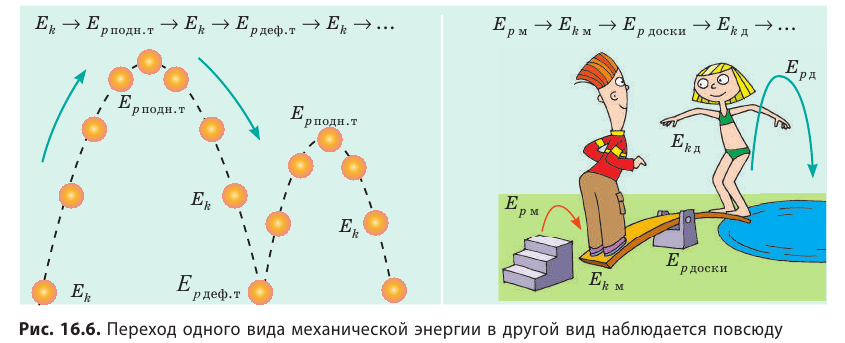
Закон сохранения полной механической энергии предполагает превращение кинетической энергии в потенциальную и наоборот (рис. 16.6). Однако сохраняется ли при этом полная механическая энергия? Наш опыт подсказывает, что нет. И действительно, закон сохранения полной механической энергии справедлив только в случаях, когда в системе отсутствует трение. Однако в природе не существует движений, не сопровождающихся трением. Сила трения всегда направлена против движения тела, поэтому при движении она совершает отрицательную работу, при этом полная механическая энергия системы уменьшается:
где 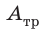
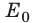
Потери энергии наблюдаются и в случае неупругого удара. Так что, при наличии трения или при неупругой деформации энергия бесследно исчезает? Казалось бы, да. Однако измерения показывают, что в результате и трения, и неупругого удара температуры взаимодействующих тел увеличиваются, то есть увеличиваются внутренние энергии тел. Значит, кинетическая энергия не исчезает, а переходит во внутреннюю энергию.
Энергия никуда не исчезает и ниоткуда не появляется: она только переходит из одного вида в другой, передается от одного тела к другому.
Алгоритм решения задач с применением закона сохранения механической энергии
- Прочитайте условие задачи. Выясните, является ли система замкнутой, можно ли пренебречь действием сил сопротивления. Запишите краткое условие задачи.
- Выполните пояснительный рисунок, на котором укажите нулевой уровень, начальное и конечное состояния тела (системы тел).
- Запишите закон сохранения механической энергии. Конкретизируйте запись, воспользовавшись данными условия задачи и соответствующими формулами для определения энергии.
- Решите полученное уравнение относительно неизвестной величины.
- Проверьте единицу, найдите значение искомой величины.
- Проанализируйте результат, запишите ответ.
Пример №2
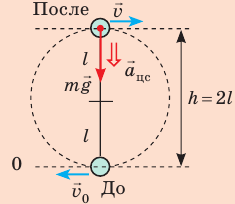
Какую минимальную скорость нужно сообщить шарику, подвешенному на нити длиной 0,5 м, чтобы он смог совершить полный оборот в вертикальной плоскости? Сопротивлением воздуха пренебречь.
Анализ физической проблемы
- Сопротивлением воздуха пренебрегаем, поэтому система «шарик — нить — Земля» является замкнутой и можно воспользоваться законом сохранения механической энергии.
- За нулевой уровень примем самое низкое положение шарика.
- В самой высокой точке траектории шарик имеет некоторую скорость, иначе он не продолжил бы вращаться, а стал бы падать вертикально вниз.
- Для определения скорости движения шарика в наивысшей точке траектории воспользуемся определением центростремительного ускорения и вторым законом Ньютона.
- Нужно найти минимальную скорость движения шарика в момент толчка, поэтому понятно, что в наивысшей точке траектории нить натянута не будет, то есть сила ее натяжения будет равна нулю.
Решение:
На рисунке отметим положения шарика в самой нижней и самой верхней точках траектории; силы, действующие на шарик в верхней точке; направление ускорения. По закону сохранения механической энергии:
Согласно второму закону Ньютона: 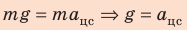
Поскольку
Подставим выражение (2) в выражение (1): 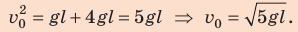
Ответ:
Выводы:
- Кинетическая энергия
- Закон сохранения и превращения механической энергии
- Работа, мощность и энергия
- Движение и силы
- Мощность в физике
- Взаимодействие тел
- Механическая энергия и работа
- Золотое правило механики
Потенциальная энергия, теория и онлайн калькуляторы
Потенциальная энергия
Определение
Определение
Потенциальной энергией ($E_p$) взаимодействующих тел называют энергию, которая зависит от взаимного расположения рассматриваемых тел. Работа ($A$) консервативных сил равна изменению потенциальной энергии системы тел находящихся во взаимодействии:
[A=E_{p1}-E_{p2}left(1right).]
Потенциальную энергию можно вычислить с точностью до произвольной постоянной величины. Добавляя ко всем значениям потенциальной энергии постоянную величину, получают новое значение потенциальной энергии. При таком изменении потенциальной энергии работа (1) не изменяется. Это результат можно сформулировать так: Ноль потенциальной энергии можно выбрать произвольно. При переходе к другому нулевому уровню потенциальной энергии величина потенциальной энергии изменится во всех точках на одну и ту же величину.
Когда говорят о потенциальной энергии тела, всегда следует указывать, в каком поле находится это тело (с каким телом взаимодействует).
Потенциальная энергия разных видов потенциальных сил
Потенциальная энергия упругих сил равна:
[E_{p_u}=frac{k{Delta x}^2}{2}left(2right),]
где $k$ — коэффициент упругости пружины; $Delta x$ — величина удлинения пружины. Потенциальная энергия упругих сил равна нулю,
когда пружина не деформирована $(Delta x=0).$
Потенциальная энергия сил Кулона в системе СИ равна:
[E_{p_k}=frac{q_1q_2}{4pi {varepsilon }_0r}left(3right),]
где $q_1{,q}_2$ — точечные электрические заряды; ${varepsilon }_0$ — электрическая постоянная; $r$ — расстояние между зарядами. Потенциальная энергия приближается к нулю, если расстояние между зарядами увеличивается до бесконечности. Если оба взаимодействующих заряда обладают одинаковыми знаками, то они отталкиваются, при этом потенциальная энергия больше нуля. Если заряды имеют противоположные знаки, то они притягиваются, а потенциальная энергия их взаимодействия отрицательна.
Потенциальную энергию сил гравитации находят как:
[E_{p_G}=-gamma frac{m_1m_2}{r}left(4right),]
где $gamma $ — гравитационная постоянная; $m_1;;m_2$ — массы материальных точек; $r$ — расстояние между точками. В данном случае потенциальная энергия является отрицательной величиной, так как сила гравитации — это сила притяжения. Потенциальная энергия стремится к нулю, если расстояние между массами бесконечно велико.
Потенциальная энергия тела поднятого над поверхностью Земли равна:
[E_{p_G}=гfrac{mMh}{R_Zleft(R_Z+hright)}left(5right),]
где $M$ — масса Земли; $R_Z$ — радиус Земли; $h$ — высота над поверхностью Земли, на которое поднято тело; $m$ — масса тела. Если расстояние от поверхности Земли до рассматриваемого тела невелико ($hll R_Z$), то можно использовать приближенную формулу расчета потенциальной энергии для этого тела в поле Земли:
[E_p=mgh left(6right).]
Единицей измерения потенциальной энергии в Международной системе единиц служит джоуль (Дж):
[left[E_pright]=Дж=Нcdot м=frac{кгcdot м^2}{с^2}.]
Потенциальная энергия и потенциальная сила
В общем случае потенциальная сила, которая действует на тело в некоторой точке потенциального поля и потенциальная энергия тела связывает соотношение:
[overline{F}=-gradE_p=-left(frac{partial E_p}{partial x}overline{i}+frac{partial E_p}{partial y}overline{j}+frac{partial E_p}{partial z}overline{k}right)left(7right),]
где $overline{i}, overline{j},overline{k}$ — единичные векторы (орты). Если поле сил имеет сферическую симметрию, то выражение (7) можно преобразовать к виду:
[F=-frac{dE_p}{dr}left(8right).]
Примеры задач с решением
Пример 1
Задание. При действии некоторой силы $F$ был поднят груз массой $m=10$кг на высоту $h=10$ м. Какой потенциальной силой обладает груз?
Решение. Сделаем рисунок.
Тело поднято над землей на высоту много меньшую, чем радиус Земли, значит для вычисления потенциальной энергии тела поднятого над Землей воспользуемся формулой:
[E_p=mgh left(1.1right).]
Поверхность Земли примем за ноль потенциальной энергии. Проведем вычисления потенциальной энергии нашего тела, принимая во внимание, что ускорение свободного падения равно $g=9,8 frac{м}{с^2}$:
[E_p=10cdot 9,8cdot 10=980 left(Джright).]
Ответ. $E_p=980$Дж
Пример 2
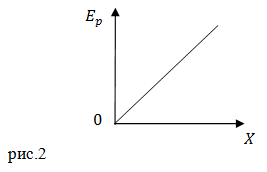
Задание. Материальная точка движется по оси OX в положительном направлении оси в силовом поле, потенциальная энергия которого задана графиком (рис.2). Как изменяется модуль ускорения этой материальной точки?
Решение. Потенциальная энергия задана прямой (рис.2), уравнение которой запишем как:
[E_p=alpha x left(2.1right),]
где $alpha =const$. Материальная точка движется под воздействием потенциальной силы, которая с потенциальной энергией связана выражением:
[overline{F}=-gradE_p=-left(frac{partial E_p}{partial x}overline{i}+frac{partial E_p}{partial y}overline{j}+frac{partial E_p}{partial z}overline{k}right)left(2.2right).]
Так как потенциальная энергия зависит только от координаты x, то формула (2.2) предстанет в виде:
[overline{F}=-frac{dE_p}{dx}overline{i} left(2.3right).]
Из уравнений (2.1) и (2.2), получим:
[overline{F}=-frac{d(alpha x)}{dx}overline{i}=-alpha overline{i} left(2.4right).]
Сила равна:
[overline{F}=moverline{a }left(2.5right),]
где $m$ — масса нашей материальной точки; $overline{a }$ — ее ускорение, тогда:
[moverline{a }=-alpha overline{i}to mleft|aright|=alpha to left|aright|=frac{alpha }{m}.]
Ответ. Модуль ускорения не изменяется.
Читать дальше: сила трения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!