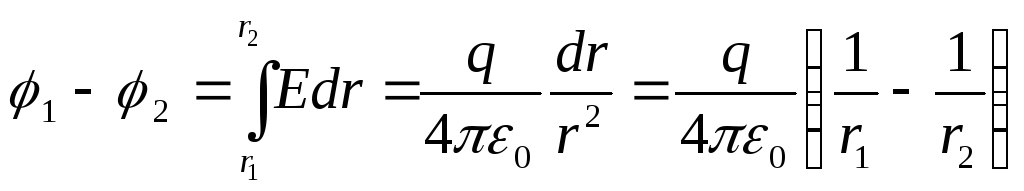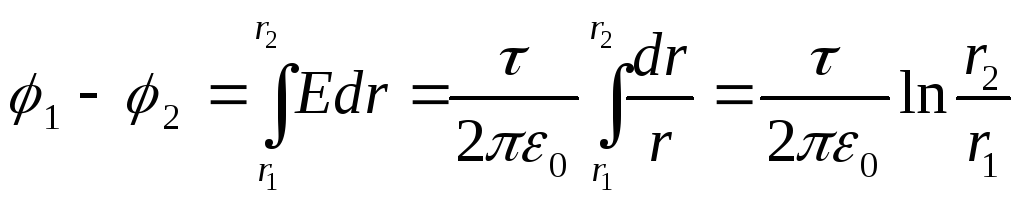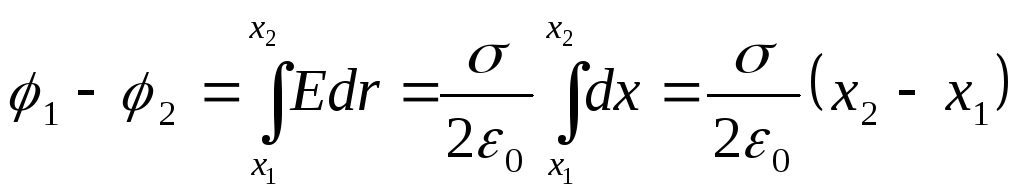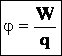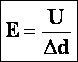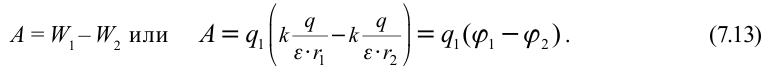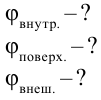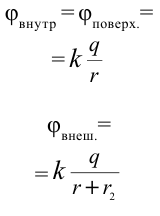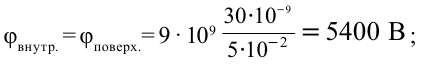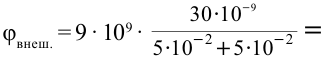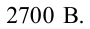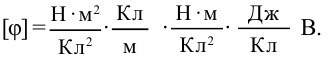Электростатическое
поле имеет две характеристики: силовую
(напряжённость) и энергетическую
(потенциал). Напряжённость и потенциал
– различные характеристики одной и той
же точки поля, следовательно, между ними
должна быть связь.
Работа по
перемещению единичного точечного
положительного заряда из одной точки
в другую вдоль оси х при условии, что
точки расположены бесконечно близко
друг к другу и х1–
х2
= dx
, равна qЕхdx.
Та же работа равна q(φ1
— φ2
)= -dφq.
Приравнивая оба выражения, можем записать
Ехdx
= -dφ
Повторив аналогичные
рассуждения для осей у и z,
можем найти вектор
:
где
— единичные векторы координатных осей
х, у, z.
Из определения
градиента следует, что
или
(12.31)
т.е. напряжённость
поля Е равна градиенту потенциала со
знаком минус. Знак минус определяется
тем, что вектор
напряжённости Е
поля направлен в сторону убывания
потенциала.
Установленная
связь между напряжённостью и потенциалом
позволяет по известной напряжённости
поля найти разность потенциалов между
двумя произвольными точками этого поля.
-
Поле равномерно
заряженной сферы радиусом
R
Напряжённость
поля вне сферы определяется по формуле
(r
>R)
Разность потенциалов
между точками r1
и r2
(r1>R;
r2
>R
) определим, используя соотношение
Потенциал сферы
получим, если r1=
R,
r2
→ ∞:
-
Поле равномерно
заряженного бесконечно длинного
цилиндра
Напряжённость
поля вне цилиндра (r
>R)
определяется формулой
(τ – линейная
плотность).
Разность потенциалов
между двумя точками, лежащими на
расстоянии r1
и r2
(r1>R;
r2
>R
) от оси цилиндра, равна
(12.32)
-
Поле равномерно
заряженной бесконечной плоскости
Напряжённость
поля этой плоскости определяется
формулой
(σ — поверхностная
плотность).
Разность
потенциалов между точками, лежащими на
расстоянии х1
и х2 от
плоскости, равна
(12.33)
-
Поле двух
разноименно заряженных бесконечных
параллельных плоскостей
Напряженность
поля этих плоскостей определяется
формулой
Разность потенциалов
между плоскостями равна
(12.34)
(d
– расстояние между плоскостями).
Примеры решения
задач
Пример 12.1.
Три точечных заряда Q1=2нКл,
Q2
=3нКл и Q3=-4нКл
расположены в вершинах равностороннего
треугольника со стороной длиной a=10см.
Определите потенциальную энергию этой
системы.
Дано:
Q1=2нКл=2∙10-9Кл;
Q2
=3нКл=3∙10-9Кл;
и
Q3=-4нКл=4∙10-9Кл;
a=10см=0,1м.
Найти:
U.
Р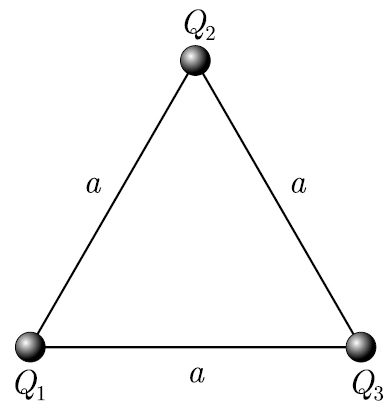
ешение:
Потенциальная
энергия системы зарядов равна
алгебраической сумме энергий взаимодействия
каждой из взаимодействующих пар зарядов,
т.е.
U=U12+U13+U23
где соответственно
потенциальные энергии одного из зарядов,
находящегося в поле другого заряда на
расстоянии а
от него, равны
;
;
(2)
Подставим формулы
(2) в выражение (1), найдём искомую
потенциальную энергию системы зарядов
Ответ:
U=-0,126мкДж.
Пример 12.2.
Определите потенциал в центре кольца
с внутренним радиусом R1=30см
и внешним R2=60см,
если на нём равномерно распределён
заряд q=5нКл.
Дано:
R1=30см=0,3м;
R2=60см=0,6м;
q=5нКл=5∙10-9Кл
Соседние файлы в папке Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
Потенциал. Разность потенциалов. Напряжение. |
|
|
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: — энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. |
|
|
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора. |
|
|
— следствие принципа суперпозиции полей (потенциалы складываютсяалгебраически). |
|
|
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах: |
|
|
Разность потенциалов |
|
|
|
|
|
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат! |
|
|
Единица разности потенциалов
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж. |
|
|
Связь между напряженностью и напряжением. |
|
|
Из доказанного выше: напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d). |
|
|
Из этого соотношения видно:
|
|
|
Эквипотенциальные поверхности. ЭПП — поверхности равного потенциала. Свойства ЭПП: — работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; — вектор напряженности перпендикулярен к ЭПП в каждой ее точке. |
|
|
|
|
|
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр. |
|
|
Потенциальная энергия взаимодействия зарядов. |
|
|
|
|
|
Потенциал поля точечного заряда |
|
|
|
|
|
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда. |
|
|
Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными. |
→ 
— Напряженность поля равна 1 В/м, если между двумя точками поля, находящимися на расстоянии 1 м друг от друга существует разность потенциалов 1 В.
Потенциал. Разность потенциалов.
Разность потенциалов (напряжение) между 2-мя точками поля равняется отношению работы поля по перемещению заряда из начальной точки в конечную к этому заряду:
,
Так как работа по перемещению заряда в потенциальном поле не зависит от формы траектории, то, зная напряжение между двумя точками, мы определим работу, которая совершается полем по перемещению единичного заряда.
Если есть несколько точечных зарядов, значит, потенциал поля в некоторой точке пространства определяется как алгебраическая сумма потенциалов электрических полей каждого заряда в данной точке:
.
Эквипотенциальной поверхностью, или поверхностью равного потенциала, является поверхность, для любых точек которой разность потенциалов равна нулю. Это означяет, что работа по перемещению заряда по такой поверхности равна нулю, следовательно, линии напряженности электрического поля перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности однородного поля представляют собой плоскости, а точечного заряда — концентрические сферы.
Вектор напряженности 
(как и сила 
) перпендикулярен эквипотенциальным поверхностям. Эквипотенциальной является поверхность любого проводника в электростатическом поле, так как силовые линии перпендикулярны поверхности проводника. Внутри проводника разность потенциалов между любыми его точками равна нулю.
Напряжение и напряженность однородного поля .
В однородном электрическом поле напряженность E в каждой точке одинакова, и работа A по перемещению заряда q параллельно на расстояние d между двумя точками с потенциалами φ1, и φ2 равна:
,
.
Т.о., напряженность поля пропорциональна разности потенциалов и направлена в сторону уменьшения потенциала. Поэтому положительный заряд будет двигаться в сторону уменьшения потенциала, а отрицательный — в сторону его увеличения.
Единицей напряжения (разности потенциалов) является вольт. Исходя из формулы , 
, разность потенциалов между двумя точками равна одному вольту, если при перемещении заряда в 1 Кл между этими точками поле совершает работу в 1 Дж.
Электрический потенциал простыми словами: формулы, единица измерения
Электрический потенциал – это скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.
Если вы хотите расширить свои знания об электрическом потенциале или сначала узнать, что такое электрический потенциал, то вы пришли по адресу.
Простое объяснение
В классической механике рассмотрение проблемы с точки зрения энергии может значительно упростить ситуацию по сравнению с рассмотрением ее с точки зрения сил, действующих на систему. В частности, в этом контексте существенную роль играет тот факт, что энергия является сохраняющейся переменной.
Также в классической электродинамике рассмотрение на энергетическом уровне оказывается очень полезным. Поэтому электрический потенциал φ (также называемый электростатическим потенциалом) определяется как отношение потенциальной энергии Eпот пробного электрического заряда и его величины электрического заряда q: φ = Eпот / q .
Возможность определения такого электрического потенциала обусловлена тем, что электрическое поле E распределения заряда и результирующая электростатическая сила Fc на пробном электрическом заряде является консервативной силой, подобной гравитационной силе.
Электрический потенциал имеет единицу измерения вольт В или также джоуль на кулон Дж / Кл .
Формулы
В этом разделе мы познакомим вас с двумя важными формулами для электрического потенциала определенных распределений электрических зарядов. Мы также кратко обсудим аналогию между электрическим потенциалом и гравитацией.
Пластинчатый конденсатор
Мы рассматриваем ситуацию, когда две плоские пластины расположены параллельно на расстоянии d друг от друга. Кроме того, пусть одна из двух пластин заряжена положительно, а другая – отрицательно. Такая комбинация также называется пластинчатым конденсатором. Обозначим точку на положительной пластине через A, а точку на отрицательной пластине через B. Тогда для разности потенциалов между этими двумя точками получим:
Здесь E – величина электрического поля между двумя пластинами, которое предполагается однородным. Такая разность потенциалов также называется электрическим напряжением, которое существует между этими двумя точками.
Из этого уравнения видно, что электрический потенциал на положительно заряженной пластине (пластина A) выше, чем потенциал на отрицательно заряженной пластине (пластина B). Поэтому положительный заряд в пластинчатом конденсаторе перемещается к отрицательной пластине. В общем случае электрическое поле – а значит, и направление движения положительного заряда – направлено в ту сторону, в которой электрический потенциал убывает быстрее всего.
Рис. 1. Пластинчатый конденсатор
Аналогия с гравитационным полем
Если умножить уравнение (приведенное выше в статье) на величину электрического заряда q пробного электрического заряда и предположить, что отрицательно заряженная пластина имеет электрический потенциал, равный нулю, то электрическая потенциальная энергия на расстоянии h от пластины равна:
Eпот. эл = q * φ = q * E * h
Здесь φ обозначает электрический потенциал в точке пробного электрического заряда.
Сравним это уравнение с потенциальной энергией в однородном гравитационном поле:
Eпот. гр = m * g * h .
Мы определяем, что количество заряда электрического q играет роль массы m, а величина электрического поля E играет роль гравитационного ускорения g. Масса, находящаяся на высоте h над землей, ускоряется по направлению к земле под действием земного притяжения.
Таким образом, масса движется в том направлении, в котором уменьшается ее потенциальная энергия. Аналогично, положительный электрический заряд движется в направлении, в котором его электрическая потенциальная энергия будет уменьшаться. Поскольку электрическая потенциальная энергия и электрический потенциал линейно связаны, это наблюдение аналогично тому, что положительно заряженная частица движется в направлении уменьшения электрического потенциала.
Рис. 2. Аналогия с гравитационным полем
Подобно потенциальной энергии, только разность потенциалов имеет физический смысл, поскольку при определении электрического потенциала необходимо произвольно определить точку отсчета, от которой затем можно обозначить другие точки в пространстве. В этом смысле электрический потенциал сам по себе не имеет реального физического смысла, поскольку для данной точки в пространстве его значение можно изменить, выбрав другую точку отсчета. Таким образом, электрический потенциал ведет себя подобно высоте, потому что вы не можете говорить о высоте, пока у вас нет точки отсчета.
На топографической карте – пути, вдоль которых высота не меняется, называются изолиниями. Аналогично, пути, вдоль которых электрический потенциал постоянен, называются эквипотенциальными линиями.
Заряженные частицы
Предположим, что частица с зарядом q находится в начале выбранной нами системы координат. Пусть положение другой точки равно r и пусть r – расстояние между двумя точками. Для электрического потенциала в точке r действует следующее соотношение:
φ (r) = q / 4 * π * ε0 * r ,
здесь ε0 – электрическая постоянная.
В этом уравнении предполагается, что под действием электрического поля положительный пробный электрический заряд переносится из бесконечности в положение r.
Примеры задач
Наконец, давайте вместе рассчитаем небольшой пример. Предположим, что электрон ускоряется от отрицательно заряженной пластины к положительно заряженной через разность потенциалов 2000 В. Как изменяется потенциальная энергия электрона?
Для разности электрических потенциалов между двумя пластинами: φB – φA = ΔEпот / q , преобразованной в искомое изменение потенциальной энергии, получаем:
Величина электрического заряда электрона равна qe = e = – 1,6 * 10 -19 Кл и поэтому получаем:
ΔEпот = e * ( φB – φA ) = – 1,6 * 10 -19 Кл * 2000 В = -3,2 * 10 -19 Дж.
Обратите внимание, что [ В ] = Дж / Кл. Кроме того, мы предположили, что пластина с точкой B заряжена положительно, поэтому перед 2000 В нет знака минус. Расчет показывает, что потенциальная энергия электрона уменьшается.
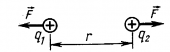
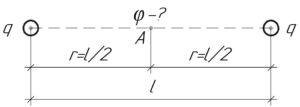
Найти потенциал электрического поля в точке, лежащей посредине между двумя
Найти потенциал электрического поля в точке, лежащей посредине между двумя зарядами по 50 нКл, расположенными на расстоянии 1 м в вакууме.
Задача №6.3.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
Так как заряды одинаковы, и они находятся на одинаковом расстоянии (r) от точки A, в которой нужно определить потенциал, значит потенциалы электрических полей в точке A, создаваемых каждым зарядом, также одинаковы. Это видно из формулы:
Здесь (k) – коэффициент пропорциональности, равный 9·10 9 Н·м 2 /Кл 2 .
Учитывая, что точка A находится посредине между двумя зарядами ((r=frac)), то:
Искомый потенциал (varphi) равен сумме потенциалов электрических полей в точке A, создаваемых каждым зарядом, поскольку потенциал – величина скалярная. Учитывая вышесказанное, имеем:
В итоге решение задачи в общем виде выглядит так:
Ответ: 1,8 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Преподаватель который помогает студентам и школьникам в учёбе.
Потенциал поля точечного заряда в физике — формулы и определение с примерами
Потенциал поля точечного заряда:
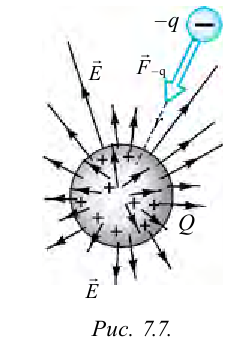
Чтобы определить силу электрического поля, мы ввели в него пробный заряд и определили силу воздействия поля на этот заряд.
Напряженность электрического поля является характеристикой силы поля.
При введении пробного заряда в поле, оно оказывает сопротивление (рис. 7.7). Для преодоления сопротивления необходимо проделать определенную работу.
Как определяется эта выполненная работа?
Эта работа превращается в потенциальную энергию взаимодействия основного заряда и введенного пробного заряда:
Знак минус в формуле показывает, что между зарядами действует сила притяжения.
Потенциальная энергия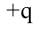 
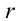
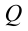
заряда, расположенного на расстоянии 
от положительного неподвижного заряда 
, определяется следующим выражением
Положительный знак в формуле показывает, что между зарядами действует сила отталкивания.
Согласно формуле потенциальная энергия равняется нулю, когда расчет производится для бесконечного расстояния. На таких расстояниях заряды не взаимодействуют.
Таким образом, электрическое поле с приобретением характеристики силы будет иметь и энергетическую характеристику. Энергетическая характеристика поля определяется величиной, которая называется потенциалом поля.
Потенциалом электрического поля точечного заряда называется величина, измеряемая отношением потенциальной энергии взаимодействия основного и введенного в поле пробного заряда к величине пробного заряда:
Потенциал точечного заряда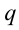 
определяется следующим образом:
Пользуясь понятием потенциала найдем работу, совершаемую при перемещении заряда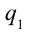 
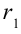
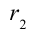
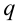
с расстояния 
на расстояние 
от заряда 
, создающего электрическое поле:
В этом выражении разница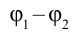 
является разницей потенциалов между точками, называется электрическим напряжением и записывается следующим образом:
Единица измерения потенциала и разность потенциалов называется Вольт (В) в честь итальянского ученого Вольта. Из формулы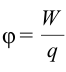 
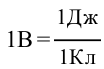
следует, что 
.
Это значит, что разность потенциалов точек равняется 1 вольту, когда заряд, равный 1 кулону, при перемещении из одной точки электрического поля в другую выполняет работу, равную 1 Дж.
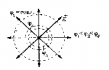
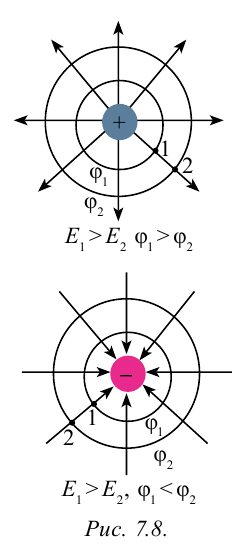
Потенциалы точек, расположенных на одинаковых расстояниях от точечного заряда, равны. Если эти точки соединить между собой, образуется поверхность, которая называется эквипотенциальной поверхностью.
Эквипотенциальная поверхность точечного заряда располагается вокруг заряда в виде сконцентрированных кругов (рис. 7.8). Силовые линии поля проходят перпендикулярно к эквипотенциальной поверхности.
Межу напряженностью электрического поля и разностью потенциалов существует следующее соотношение:
где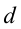 
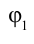
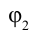
–расстояние между точками, потенциал которых равен 
и 
.
Отсюда получаем единицу измерения напряженности поля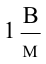 
.
Образец решения задачи:
В металлическую сферу радиусом 5 см, висящую в воздухе, подали заряд 30 нКл. Нужно найти потенциалы поля в точках, находящихся в 2 см от центра заряженной сферы, на поверхности сферы и удаленной от поверхности на расстояние 5 см.
Дано:
Найти:
Формула:
Решение:
Единица измерения: 
Ответ: 5400 В; 2700 В.
- Работа электрического поля при перемещении заряда в физике
- Энергия электрического поля
- Электрическое поле заряженных неподвижных тел
- Напряженность электрического поля
- Электростатика
- Закон сохранения заряда в физике
- Электрическое поле заряженного шара
- Электрические явления в физике
№
37. Связь между напряженностью и разностью потенциалов электрического поля.
Напряженность
электрического поля – величина, численно равная силе, действующей на заряд.
Потенциал φ – величина, численно равная
потенциальной энергии заряда.
Каждой точке
электрического поля соответствуют определенные значения потенциала и напряженности.
Найдем связь напряженности электрического поля с потенциалом.
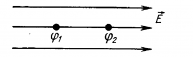
Пусть заряд q перемещается
в направлении вектора напряженности однородного электрического поля 
из точки 1 в точку 2,
находящуюся на расстоянии 
от точки 1 (рис.93, стр. 119).
Электрическое поле совершает работу: A=qEΔd
Эту работу согласно формуле можно выразить через
разность потенциалов в точках 1 и 2: A=qU
Приравнивая выражения для работы, найдем модуль
вектора напряженности поля:
qEΔd=qU
E= 
= 
Где U —
разность потенциалов между точками 1 и 2, которые
связаны вектором перемещения 
, совпадающим по направлению с вектором напряженности .
Формула E=
показывает: чем меньше меняется потенциал на
расстоянии 
, тем меньше напряженность электростатического
поля. Если потенциал не меняется совсем, то напряженность поля равна нулю.
Так как при
перемещении положительного заряда в направлении вектора напряженности 
электростатическое поле совершает
положительную работу 
, то потенциал 
больше потенциала 
.
Следовательно, напряженность
электрического поля направлена в сторону убывания потенциала.
Любое
электростатическое поле в достаточно малой области пространства можно считать
однородным. Поэтому формула E= справедлива
для произвольного электростатического поля, если только расстояние 
настолько мало, что изменением
напряженности поля на этом расстоянии можно пренебречь.
Единица напряженности
электрического поля. Единицу напряженности электрического поля в СИ
устанавливают, используя последнюю формулу . Напряженность
электрического поля численно равна единице, если разность потенциалов между
двумя точками на расстоянии 1 м в однородном поле равна 1
В. Наименование этой единицы — вольт на метр (В/м).
Напряженность можно
также выражать в ньютонах на кулон. Действительно,
Эквипотенциальные поверхности.
Потенциал
электростатического поля представляет собой функцию, меняющуюся от точки к
точке. Однако, во всяком реальном случае можно выделить совокупность точек,
потенциалы которых одинаковы.
Геометрическое
место точек постоянного потенциала называется поверхностью равногопотенциала
или эквипотенциальной поверхностью.
Возьмем
равномерно заряженную бесконечную плоскость. Поле, создаваемое та
кой
плоскостью однородно, а линии напряженности нормальны к плоскости.
Отсюда
следует, что работа перемещения заряда из некоторой точки В1
в любую другую точку В2,
находящуюся на таком же расстоянии от заряженной поверхности, что и точка В1равна
нулю. Действительно, при перемещении некоторого заряда q по прямой В1
В2 сила, действующая на заряд со стороны поля, будет все время
перпендикулярна к перемещению, а, следовательно, ее работа равна нулю. Но
эта работа может быть представлена, с другой стороны, в виде:
A
= q(φ1— φ2)= 0
где
φ1 и φ2 – соответственно
потенциалы точек В1 и В2. Отсюда, так как
А
= 0, то φ1= φ2, т.е., потенциалы
точек, равноудаленных от заряженной
плоскости,
одинаковы. Таким образом, поверхности равного потенциала (эквипотенциальные
поверхности) являются плоскостями, параллельными заряженной плоскости. Если
плоскость заряжена положительно, то значение потенциала убывает по мере
удаления от заряженной плоскости. Очевидно, что поверхности равного потенциала
расположены симметрично по обе стороны от заряженной плоскости.
Эквипотенциальные
поверхности поля точечного заряда это сферы с радиусом
r,
центр которых находится в центре точечного заряда, т.е. φ=
.
На
рисунке 95 вектор напряженности E перпендикулярен эквипотенциальным
поверхностям.
Покажем,
что вектор напряженности перпендикулярен эквипотенциальной поверхности.
Рассмотрим работу по перемещению заряда по поверхности равного потенциала
на малом участке пути ∆d. При этом, работа электрической
силы F=qE на данном пути будет:
A=F∆dcos
α= qE∆dcos
α, где α – угол между направлением силы f
и
перемещением ∆d. С другой стороны, эта работа может
быть выражена как произведение величины перемещающегося заряда на разность
потенциалов в начальном и конечном положениях заряда, т.е. A
= q(φ1— φ2)
Так
как перемещение идет по эквипотенциальной поверхности, то разность потенциалов (φ1—
φ2)=0 и qE∆dcos
α=0, или cosα= 0,
значит α = 900 т.е.
угол
между направлением силы F и
перемещением ∆d равен 900.
Но F и Е совпадают, поэтому угол
между E и ∆d, α=900, т.е.
направление вектора напряженности электростатического поля всегда
перпендикулярно к эквипотенциальной поверхности.
Значит, если провести поверхность,
перпендикулярную в каждой ее точке силовым линиям, то при перемещении заряда
вдоль этой поверхности работа не совершается. А это означает, что все точки
поверхности, перпендикулярной силовым линиям, имеют один и тот же потенциал.
Поверхности равного потенциала называют эквипотенциальными.
Эквипотенциальные
поверхности однородного
поля представляют собой плоскости (рис.94, стр. 120), а поля точечного
заряда — концентрические сферы (рис. 95, стр. 120).
Подобно силовым линиям, эквипотенциальные
поверхности качественно характеризуют распределение поля в пространстве. Вектор напряженности перпендикулярен
эквипотенциальным поверхностям и направлен в сторону уменьшения потенциала.
Эквипотенциальные
поверхности строятся обычно так, что разность потенциалов между двумя соседними
поверхностями постоянна. Поэтому согласно формуле расстояния между соседними
эквипотенциальными поверхностями увеличиваются по мере удаления от точечного
заряда, так как напряженность поля уменьшается.
Эквипотенциальные
поверхности однородного поля расположены на равных расстояниях друг от друга.
Эквипотенциальной является
поверхность любого проводника в электростатическом поле. Ведь силовые
линии перпендикулярны поверхности проводника. Причем не только поверхность, но
и все точки внутри проводника имеют один и тот же потенциал. Напряженность поля
внутри проводника равна нулю, значит, равна нулю и разность потенциалов между
любыми точками проводника.
Модуль напряженности электростатического поля
численно равен разности потенциалов между двумя близкими точками в этом поле,
деленной на расстояние между этими точками.
В однородном электрическом
поле напряженностью Е = 2*105 В/м
переместили заряд q = –20 нКл в направлении
силовой линии поля на расстояние d = 10 см. Найти работу
поля А, изменение потенциальной
энергии поля ΔWп и напряжение (разность
потенциалов) U между начальной и конечной
точками перемещения.
Домашнее
задание
§ 45-46,
вопросы.
