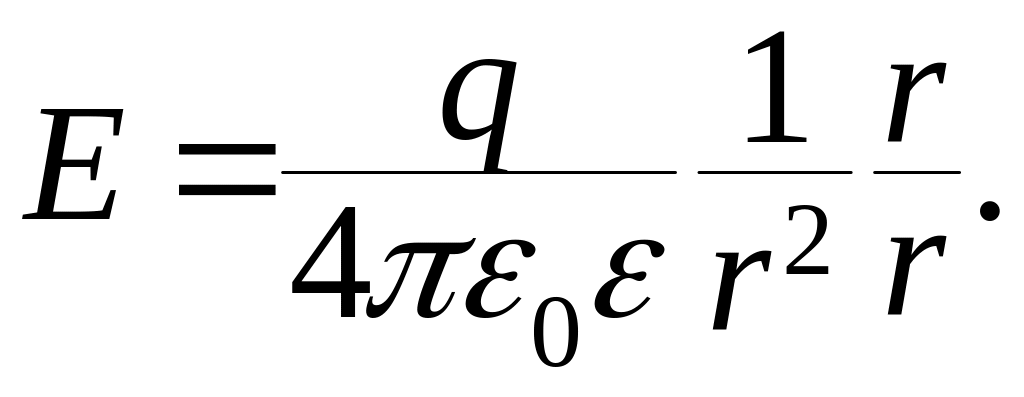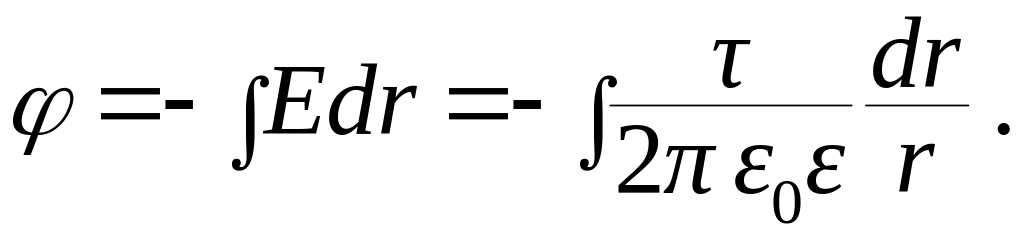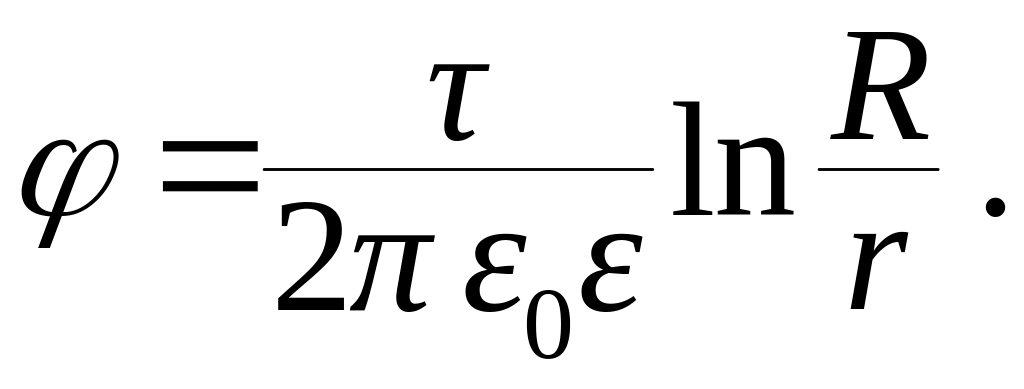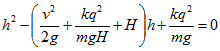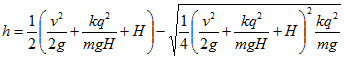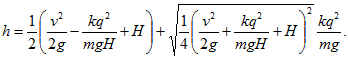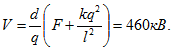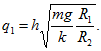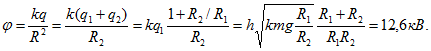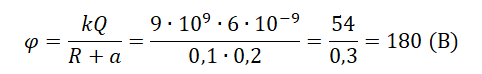Найдем
потенциал, создаваемый проводящей
заряженной сферой радиуса R. Как известно,
внутри сферы (при r
< R)
E
= 0;
вне сферы (при r
> R)
С учетом формулы (13.18), связывающей
напряженность и потенциал, находим:
1.
,
отсюда
= const;
2.
(13.21)
Постоянную
C
выберем из условия, что
при
,
отсюда C
= 0. Потенциал внутри проводящей сферы
имеет одинаковое значение во всех точках
внутри сферы и равен потенциалу на
поверхности:
(13.22)
Потенциал
вне заряженной сферы равен потенциалу
точечного заряда, помещенного в центр
сферы.
На
рис. 13.6 приведен график зависимости
потенциала
от расстояния до центра сферы r.
Для
проводящего шара получим тот же результат,
что и для сферы.
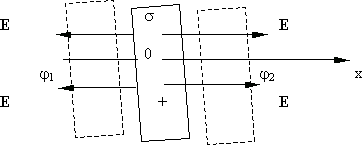
Найдем
теперь потенциал заряженной бесконечной
плоскости с поверхностной плотностью
заряда
(рис. 13.7).
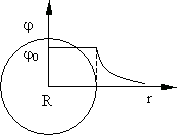
Рис.
13.6.
Напряженность
электрического поля плоскости:
.
Потенциал
получим в виде
(13.23)
Выберем
начало отсчета потенциала так, чтобы
при x
= 0, потенциал был равен 0, тогда C
= 0.
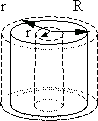
Рис.
13.7. Рис. 13.8.
Потенциал электрического поля заряженной плоскости:
171
(13.24)
Разность
потенциалов между двумя точками поля
(13.25)
Потенциал электрического поля заряженного цилиндра:
Потенциал
заряженного бесконечного цилиндра с
линейной плотностью
найдем из соотношения:
(13.26)
Потенциал
поля внутри цилиндра (рис. 13.8) является
постоянной величиной при r
< R и равен
потенциалу на поверхности цилиндра,
т.к. E = 0
внутри цилиндра. Потенциал вне заряженного
цилиндра (r
> R):
Если принять, что потенциал j
на поверхности цилиндра (при r
= R)
равен нулю, тогда постоянная
Потенциал
вне цилиндра имеет такую же величину,
как и потенциал заряженной нити,
помещенной на оси цилиндра
(13.27)
Глава 14. Диэлектрики в электростатическом поле
14.1. Проводники и диэлектрики
По
электрическим свойствам твердые тела
можно разделить на проводники и
диэлектрики. Основным отличием
диэлектриков от проводников является
отсутствие в диэлектриках свободных
зарядов, способных перемещаться в
электрическом поле. Проводники содержат
свободные заряды, носителями которых
являются электроны, не связанные с
атомами.
Каждое
вещество может проявлять свойства
диэлектрика и проводника, в зависимости
от внешних условий и времени наблюдения.
Так, заряженный шар из диэлектрика,
например из эбонита, подвешенный на
шелковой нити, может долго сохранять
свой заряд, но через длительное время
заряд все же стечет с поверхности шара.
Если
заряженное тело находится вблизи
другого, первоначально незаряженного
тела, то в проводниках и диэлектриках
происходит электростатическая индукция,
и на соседнем теле появятся заряды
противоположного знака. В проводнике
заряд распределится по поверхности,
внутри проводника заряд будет равен
0, поэтому напряженность электрического
поля E
= 0. В диэлектрике связанные заряды
распределяются по всему объему.
Если
проводник поместить во внешнее
электростатическое поле, то на концах
проводника появятся заряды разного
знака. Если разрезать проводник на две
части, то на каждой останется заряд
одного знака.
В
диэлектрике, помещенном в электростатическое
поле, также появятся на концах разноименные
заряды, но эти заряды нельзя отделить.
В разрезанном диэлектрике суммарный
заряд каждой его части будет равен
нулю.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание книги
Предыдующая страница
§9. Электрическое поле и его свойства
9.11 Примеры расчета потенциалов электростатических полей.
Поле равномерно заряженной сферы.
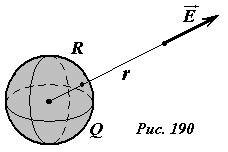
Пусть электрическое поле создается зарядом Q, равномерно распределенным по поверхности сферы радиуса R (Рис. 190). Для вычисления потенциала поля в произвольной точке, находящейся на расстоянии r от центра сферы, необходимо вычислить работу, совершаемую полем при перемещении единичного положительного заряда от данной точки до бесконечности. Ранее мы доказали, что напряженность поля равномерно заряженной сферы вне ее эквивалентно полю точечного заряда, расположенного в центре сферы. Следовательно, вне сферы потенциал поля сферы будет совпадать с потенциалом поля точечного заряда
(~varphi(r) = frac{Q}{4 pi varepsilon_0 r}) . (1)
В частности, на поверхности сферы потенциал равен (~varphi_0 = frac{Q}{4 pi varepsilon_0 R}) . Внутри сферы электростатическое поле отсутствует, поэтому работа по перемещению заряда из произвольной точки, находящейся внутри сферы, на ее поверхность равна нулю A = 0, поэтому и разность потенциалов между этими точками также равна нулю Δφ = —A = 0. Следовательно, все точки внутри сферы имеют один и тот же потенциал, совпадающий с потенциалом ее поверхности (~varphi_0 = frac{Q}{4 pi varepsilon_0 R}) .
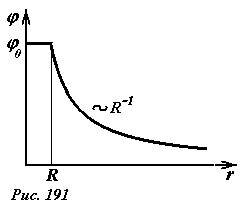
Итак, распределение потенциала поля равномерно заряженной сферы имеет вид (Рис. 191)
(~varphi(r) = left{begin{matrix} frac{Q}{4 pi varepsilon_0 R} , mbox{ npu } r < R \ frac{Q}{4 pi varepsilon_0 r} , mbox{ npu } r > R end{matrix}right.) . (2)
Обратите внимание, поле внутри сферы отсутствует, а потенциал отличен от нуля! Этот пример является яркой иллюстрацией, того, что потенциал определяется значением поля от данной точки до бесконечности.
Поле равномерно заряженного кольца.
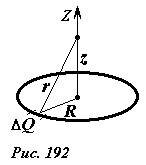
Вычислим потенциал поля, создаваемого зарядом Q, равномерно распределенным по тонкому кольцу радиуса R, причем ограничимся расчетом потенциала поля только на оси кольца (Рис. 192). Ранее мы вычислили напряженность поля на оси кольца, как функцию расстояния до его центра. Поэтому для вычисления потенциала можно, в принципе, подсчитать работу, совершаемую полем при перемещении заряда от данной точки до бесконечности. Однако, в данном случае проще воспользоваться принципом суперпозиции для потенциала поля. Для этого мысленно разобьем кольцо на малые участки, несущие заряд ΔQk. Тогда в точке, находящейся на расстоянии z от его центра, этот заряд создает поле, потенциал которого равен
(~delta varphi_k = frac{Delta Q_k}{4 pi varepsilon_0 r} = frac{Delta Q_k}{4 pi varepsilon_0 sqrt {R^2 + z^2}}) .
Так как все точки кольца находятся на одинаковом расстоянии (~r = sqrt {R^2 + z^2}) от рассматриваемой точки, то суммирование потенциалов полей, создаваемых зарядами ΔQk сводится к суммированию самих зарядов
(~varphi = sum_{k} {delta varphi_k} = sum_{k} {frac{Delta Q_k}{4 pi varepsilon_0 sqrt {R^2 + z^2}}} = frac{1}{4 pi varepsilon_0 sqrt {R^2 + z^2}} sum_{k} {Delta Q_k} = frac{Q}{4 pi varepsilon_0 sqrt {R^2 + z^2}}) . (3)
График этой функции показан на рисунке. Там же повторен график зависимости напряженности поля кольца на его оси от расстояния до центра кольца. Напомним, что значения потенциала φ(z0) в точке с координатой z0 численно равно площади под графиком зависимости E(z) в интервале от z0 до (~z to infty) .
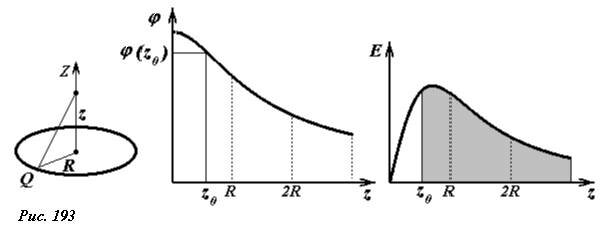
Обратите внимание – так как проекция вектора напряженности не изменяет свой знак, то функция φ(z) является монотонной.
Поле равномерно заряженной бесконечной пластины.
Ранее мы показали, что электрическое поле, создаваемое бесконечной равномерно заряженной пластиной является однородным, то есть напряженность поля одинакова во всех точках, причем вектор напряженности направлен перпендикулярно плоскости, а его модуль равен (~E_0 = frac{sigma}{2 varepsilon_0}) . Семейством силовых линий такого поля явяется набор параллельных прямых, перпендикулярных пластине. На рис. 194 так же изображен график зависимости проекции вектора напряженности поля Ex на ось Z перпендикулярную пластине (начало отсчета этой оси расположим на пластине). Понятно, что потенциал данного поля зависит только от координаты z, то есть эквипотенциальные поверхности в данном случае являются плоскостями, параллельными заряженной пластине.
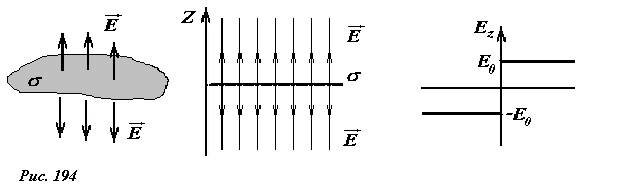
При традиционном выборе нулевого уровня потенциала (~varphi(z to infty) = 0) , потенциал произвольной точки равен работе по перемещению единичного положительного заряда из данной точки на бесконечность. Так как модуль напряженности постоянен, то такая работа (а, следовательно, и потенциал) оказывается равной бесконечности! Следовательно, указанный выбор нулевого уровня потенциала в данном случае непригоден.
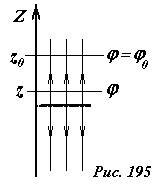
Поэтому следует воспользоваться произволом выбора нулевого уровня. Достаточно выбрать произвольную точку с координатой z = z0, и приписать ей произвольное значение потенциала φ(z0) = φ(0) (Рис. 195). Теперь, чтобы вычислить значение потенциала в произвольной точке φ(z), можно воспользоваться соотношением между напряженностью и потенциалом поля (~Delta varphi = — vec E cdot Delta vec r) . Учитывая, что в данном случае напряженность поля постоянна (при z > 0) это выражение записывается в виде
(~varphi(z_0) — varphi(z) = -E_0 (z_0 — z)) ,
из которого следует искомая зависимость потенциала от координаты (при z > 0)
(~varphi(z) = varphi_0 — E_0 (z — z_0)) . (4)
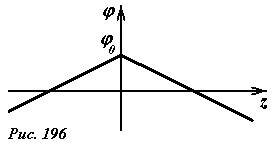
В частности, можно задать произвольное значение потенциала самой пластины, то есть положить при z = z0 = 0 φ = φ(0). Тогда значение потенциала в произвольной точке определяется функцией
(~varphi(z) = varphi_0 — E_0 |z|) , (5)
график которой показан на рисунке 196.
То, что потенциал относительно бесконечности оказался бесконечно большим, вполне очевидно – ведь и бесконечная пластина обладает бесконечно большим зарядом. Как мы уже подчеркивали, такая система является идеализацией – бесконечных пластин не существует. В реальности все тела имеют конечные размеры, поэтому для них традиционный выбор нулевого потенциала возможен, правда в этом случае распределение поля может быть очень сложным. В рамках же рассматриваемой идеализации удобнее воспользоваться использованным нами выбором нулевого уровня.
Задание для самостоятельной работы.
-
Покажите, что при произвольном выборе нулевого уровня потенциала функция (4) может быть обобщена на все значения координаты z (в том числе и отрицательные) следующим образом
-
(~varphi(z) = varphi_0 — E_0 (|z| — z_0)) .
- Постройте график этой функции.
-
Поле двух параллельных равномерно заряженных пластин.
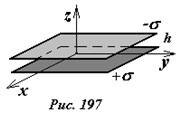
Найдем распределение потенциала поля, создаваемого двумя одинаковыми равномерно заряженными параллельными пластинами, заряды которых равны по модулю и противоположны по знаку [1] (Рис. 197). Обозначим поверхностную плотность заряда на одной пластине +σ, а на другой —σ . Расстояние между пластинами h будем считать значительно меньшим размеров пластин. Введем систему координат, ось z которой перпендикулярна пластинам, начало координат разместим по средине между пластинами. Очевидно, для бесконечно больших пластин все характеристики поля (напряженность и потенциал) зависят только от координаты z. Для расчета напряженности поля в различных точках пространства воспользуемся полученным выражением для напряженности поля, создаваемого бесконечной равномерно заряженной пластиной и принципом суперпозиции.
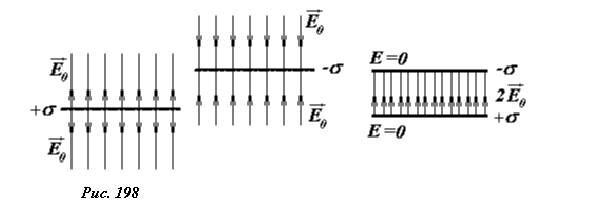
Каждая равномерно заряженная пластина создает однородное поле, модуль напряженности которого равен (~E_0 = frac{sigma}{2 varepsilon_0}) , а направления указаны на рисунке 198.
Складывая напряженности полей по принципу суперпозиции, получим, что в пространстве между пластинами напряженность поля (~E = 2E_0 = frac{sigma}{varepsilon_0}) вдвое превышает напряженность поля одной пластины (здесь поля отдельных пластин параллельны), а вне пластин поле отсутствует (здесь поля отдельных пластин противоположны).
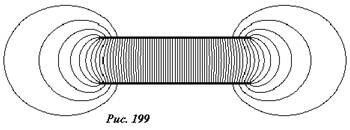
Строго говоря, для пластин конечных размеров поле не является однородным, силовые линии поля пластин конечных размеров показаны на рисунке 199. Наиболее сильные отклонения от однородности наблюдаются вблизи краев пластин (часто эти отклонения называют краевыми эффектами). Однако, в области прилегающей к середине пластин поле с высокой степенью точности можно считать однородным, то есть в этой области можно пренебречь краевыми эффектами. Заметим, что погрешности такого приближения тем меньше, чем меньше отношение расстояния между пластинами к их размерам.
Для однозначного определения распределения потенциала поля, необходимо выбрать уровень нулевого потенциала. Будем считать, что потенциал равным нулю в плоскости расположенной по средине между пластинами, то есть, положим φ = 0 при z = 0.
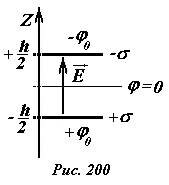
Не смотря на произвол в выборе нулевого уровня потенциала, наш выбор может быть логически обоснован на основании симметрии системы. Действительно, рассматриваемая система зарядов зеркально повторяет себя при зеркальном отражении относительно плоскости z = 0 и одновременном изменении знаков зарядов. Поэтому желательно, чтобы и распределение потенциала обладало такой же симметрией: восстанавливалось при зеркальном отражении с одновременным изменением знака всех функций поля. Выбранный нами способ выбора нулевого потенциала удовлетворяет такой симметрии.
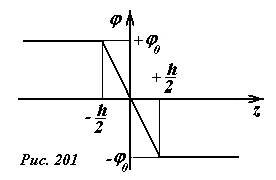
Обозначим потенциал положительно заряженной пластины +φ0, тогда потенциал отрицательно заряженной пластины будет равен —φ0. Эти потенциалы легко определить, используя найденное значение напряженности поля между пластинами и связь между напряженностью и разностью потенциалов электрического поля. Уравнение этой связи в данном случае имеет вид φ0 — (-φ0) = Eh. Из этого соотношения определяем значения потенциалов пластин (~varphi_0 = frac{sigma h}{2 varepsilon_0}) . Учитывая, что между пластинами поле однородное (поэтому потенциал изменяется линейно), а вне пластин поле отсутствует (поэтому здесь потенциал постоянен), зависимость потенциала от координаты z имеет вид (рис. 201)
(~varphi(z) = left{begin{matrix} +varphi_0 , & mbox{ npu } z < — frac{h}{2} \ +2 frac{varphi_0}{h}z , & mbox{ npu } — frac{h}{2} < z < + frac{h}{2} \ -varphi_0 , & mbox{ npu } z > + frac{h}{2} end{matrix}right.) . (6)
Задания для самостоятельной работы.
- Во всех рассмотренных примерах проделайте обратную операцию: по найденному распределению потенциала с помощью формулы (~E_x = -frac{Delta varphi}{Delta x}) рассчитайте напряженности рассмотренных полей.
- Строго выведите формулу (6).
- Качественно объясните следующий «парадокс». В поле плоского конденсатора неоднозначно определен потенциал «бесконечности»: при движении в положительном направлении оси Z потенциал «бесконечности» оказался равным -φ0; при движении в отрицательном направлении оси Z — +φ0 , при движении вдоль осей X или Y- равен нулю. Так чему равен потенциал «бесконечности» в реальной системе двух пластин конечных размеров?
Примечания
- ↑ Такая система называется плоским конденсатором, подробнее эти устройства мы будем изучать позже.
Следующая страница
Примеры решения задач по физике — концентрические проводящие сферы
Суббота, 25 февраля, 2012
Среди школьных задач по физике особняком стоят те, которые связаны с концентрическими проводящими сферами. Эти сферы могут быть заряжены, заземлены, могут находиться в поле внешних зарядов и т. д., вариаций много. В школьном курсе физики эти задачи являются одними из самых сложных. Не в последнюю очередь, конечно, непонимание данного материала связано с неспособностью учителей объяснить его грамотно и доступно. Итак, попробуем разобраться, что это за проводящие сферы и с чем их едят.
Тексты заданий я взял из сборника задач по физике для подготовительных отделений вузов.
Задача 1. Сфера радиуса r, которой сообщен заряд q, окружена концентрической тонкостенной проводящей сферической оболочкой радиуса R, заряд которой равен Q. Определите потенциалы сфер φin (внутренней) и φex (внешней).
Решение. Потенциал на поверхности внутренней сферы φex складывается из двух потенциалов: внешней сферы φ1 и собственно внутренней сферы φ2.
Потенциал внешней сферы φ1 в каждой точке ее внутреннего объема одинаков и равен потенциалу на ее поверхности (подробнее о решении задач на тему «Потенциал» читайте в этой статье):
Потенциал внутренней сферы φ2 определяется известным соотношением:
Тогда общий потенциал φin на поверхности внутренней сферы равен:
Потенциал на поверхности внешней сферы также складывается из двух потенциалов: внутренней сферы φ’1 и собственно внешней сферы φ’2.
Потенциал внутренней сферы φ’1 на расстоянии R от ее центра определяется известным соотношением:
Формула, определяющая потенциал внешней сферы φ’2 на ее поверхности, также хорошо известна:
Тогда общий потенциал на поверхности внешней сферы равен:
Задача 2. Металлический шар радиуса R1, заряженный до потенциала φ, окружают тонкой сферической проводящей оболочкой радиуса R2. Определите потенциал шара φ1 после того, как он будет соединен проводником с оболочкой. Первоначальный заряд оболочки равен нулю, центры оболочки и шара совпадают.
Решение. До соединения сфер проводником заряд первой был равен:
После соединения часть заряда с внутренней сферы перетекло на внешнюю. Ток прекратился в тот момент, когда потенциал шара стал равен потенциалу внешней оболочки. Удобнее поэтому искать не потенциал шара, а равный ему потенциал внешней оболочки. В соответствии с результатами, полученными в предыдущей задаче, этот потенциал определяется выражением:
где q1 и q2 — заряды шара и внешней оболочки после соединения их проводником соответственно. По закону сохранения заряда q = q1 + q2. После несложных преобразований получаем:
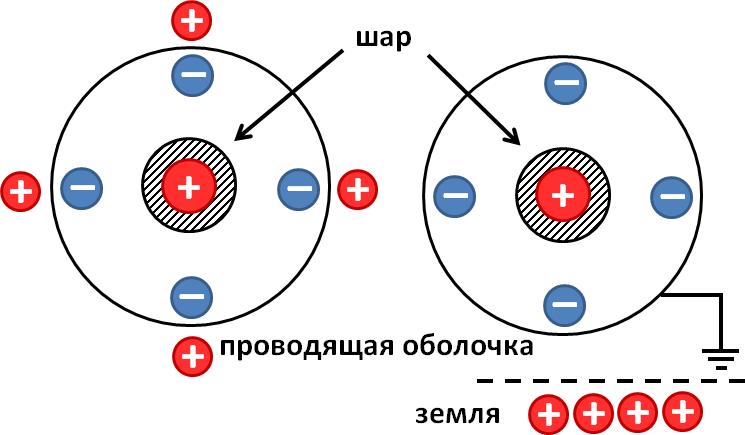
Задача 3. Металлический шар радиуса R1, заряженный до потенциала φ, окружают концентрической сферической проводящей оболочкой радиуса R2. Чему станет равен потенциал шара φ‘, если заземлить оболочку?
Начнем с рисунка к решению задачи:
После заземления проводящей оболочки весь положительный заряд, образовавшийся на ней вследствие явления электростатической индукции, стекает на землю. На ней остается только отрицательный заряд, поскольку он притягивается к положительному заряду внутренней сферы
Решение. Зная потенциал шара в начальный момент времени и его радиус, можно найти заряд на нем:
Вследствие явления электростатической индукции на внешней оболочке должно произойти разделение заряда. Отрицательный заряд перетечет на внутреннюю поверхность оболочки, положительный — на внешнюю (см. рисунок). Это же явление возникало и в предыдущих задачах, но мы не принимали его во внимание. Почему? В условии задач было указано, что оболочка тонкая, и такое «разбегание» зарядов не приводило к сколько-нибудь существенному изменению конфигурации электростатического поля.
В этой задаче учет данного явления важен, поскольку оболочку заземляют. После заземления положительный заряд с оболочки стечет на землю, останется лишь отрицательный q2, поскольку он притягивается к положительному заряду q1 внутренней сферы. Потенциал заземленной оболочки станет равен потенциалу земли, то есть нулю. В этой связи и в соответствии с результатом, полученным при решении первой задачи, получаем равенство:
Используя выражение для расчета потенциала внутренней сферы подобной системы, полученное в первой задаче, находим окончательно требуемый потенциал шара:
Опыт показывает, что редко кто понимает решение этих задач во всех деталях с первого раза. Обычно приходится долго и настойчиво разъяснять ученикам все те мелочи, без осознания которых решение сводится к пустым преобразованиям буквенных выражений с целью получения приведенного в конце учебника ответа. Понять физическую сущность этих задач и научиться применять полученные знания в будущем не просто. Однако в этом и состоит основная методическая ценность данной темы в школьном курсе физики. Лучшим помощником в ее изучении непременно станет профессиональный репетитор, грамотный наставник, который сможет придумать понятное именно вам объяснение и ответит на все возникшие вопросы. Кстати, если таковые имеются, вы можете задать их ниже в комментариях.
Репетитор по физике и математике
Сергей Валерьевич
Учителя только открывают двери, дальше вы идете сами.
© Китайская пословица
Решение:
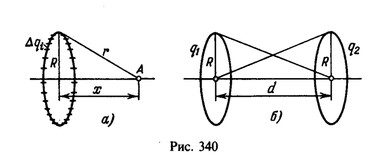
15 Два параллельных тонких кольца радиуса R расположены на расстоянии d друг от друга на одной оси. Найти работу электрических сил при перемещении заряда qo из центра первого кольца в центр второго, если на первом кольце равномерно распределен заряд q1, а на втором — заряд q2.
Решение:
Найдем потенциал, создаваемый зарядом q, находящимся на кольце, в точке А на оси кольца, расположенной на расстоянии
х от его центра (рис. 340, а) и, следовательно, на расстояниях от точек, лежащих на кольце. Разобьем кольцо на отрезки, малые по сравнению с расстоянием r. Тогда заряд
, находящийся на каждом отрезке (i — номер отрезка), можно рассматривать как точечный. Он создает в точке А потенциал
. Потенциал, создаваемый в точке А всеми отрезками кольца (отстоящими от этой точки на одно и то же расстояние r), будет
В скобках стоит сумма зарядов всех отрезков, т. е. заряд всего кольца q; поэтому
Потенциал Ф1 поля в центре первого кольца складывается из потенциала, создаваемого зарядом q1, находящимся на первом кольце, для которого х=0, и потенциала, создаваемого зарядом q2, находящимся на втором кольце, для которого x=d (рис. 340, б). Аналогично находится потенциал в центре второго кольца:
Окончательно для работы имеем
16 На тонком кольце радиуса R равномерно распределен заряд q. Какова наименьшая скорость υ, которую необходимо сообщить находящемуся в центре кольца шарику массы т с зарядом qo, чтобы он мог удалиться от кольца в бесконечность?
Решение:
Если заряды qo и q одного знака, то удалить шарик от кольца в бесконечность можно, сообщив ему бесконечно малую скорость. Если же знаки зарядов разные, то сумма кинетической и потенциальной энергий шарика в центре кольца должна быть равна нулю, так как она равна нулю в бесконечности: , где φ=kq/R — потенциал в центре кольца (см. задачу 17); отсюда
17 На шарик радиуса R=2 см помещен заряд q=4 пКл. С какой скоростью подлетает к шарику электрон, начавший движение из бесконечно удаленной от него точки?
Решение:
18 Между горизонтально расположенными пластинами плоского конденсатора с высоты Н свободно падает незаряженный металлический шарик массы т. На какую высоту h после абсолютно упругого удара о нижнюю пластину поднимется шарик, если в момент удара на него переходит заряд q? Разность потенциалов между пластинами конденсатора равна V, расстояние между пластинами равно d.
Решение:
Внутри конденсатора имеется однородное электрическое поле с напряженностью Е= V/d, направленной вертикально. После удара шарик приобретает заряд того же знака, что и нижняя пластина конденсатора. Поэтому на него будет действовать со стороны электрического поля сила F=qE=qV/d, направленная вверх. Согласно закону сохранения энергии изменение энергии равно работе внешних сил (в данном случае — электрических). Учитывая, что удар абсолютно упругий и что в начальный и конечный моменты шарик имеет лишь потенциальную энергию в поле силы тяжести, получимоткуда
19 Два шарика с одинаковыми зарядами q расположены на одной вертикали на расстоянии Н друг от друга. Нижний шарик закреплен неподвижно, а верхний, имеющий массу m, получает начальную скорость v, направленную вниз. На какое минимальное расстояние h приблизится верхний шарик к нижнему?
Решение:
Согласно закону сохранения энергии
где qV—работа электрических сил, V=kq/H—kq/h — разность потенциалов точек начального и конечного положения верхнего шарика. Для определения h получаем квадратное уравнение:
Решая его, найдем
(знак плюс перед корнем соответствовал бы максимальной высоте, достигнутой шариком, если бы он получил ту же начальную скорость, направленную вверх).
20 Найти максимальное расстояние h между шариками в условиях предыдущей задачи, если неподвижный шарик имеет отрицательный заряд q, а начальная скорость v верхнего шарика направлена вверх.
Решение:
21 Электрон, пролетая в электрическом поле путь от точки а к точке b, увеличил свою скорость с νa=1000 км/с до νab = 3000 км/с. Найти разность потенциалов между точками а и b электрического поля.
Решение:
Работа, совершенная над электроном электрическим полем, идет на увеличение кинетической энергии электрона:
откуда
где γ— удельный заряд электрона. Разность потенциалов отрицательна. Так как электрон имеет отрицательный заряд, то скорость электрона увеличивается при его движении в сторону возрастания потенциала.
22 В плоский конденсатор влетает электрон со скоростью ν = 20 000 000 м/с, направленной параллельно пластинам конденсатора. На какое расстояние h от своего первоначального направления сместится электрон за время пролета конденсатора? Расстояние между пластинами d=2 см, длина конденсатора l=5 см, разность потенциалов между пластинами v=200 В.
Решение:
За время пролета t = l/v электрон смещается в направлении действия силы на расстояние
где γ — удельный заряд электрона.
23 Положительно заряженная пылинка массы г находится в равновесии внутри плоского конденсатора, пластины которого расположены горизонтально. Между пластинами создана разность потенциалов V1=6000 В. Расстояние между пластинами d=5см. На какую величину необходимо изменить разность потенциалов, чтобы пылинка осталась в равновесии, если ее заряд уменьшился на qo=1000 e?
Решение:
На пылинку действуют сила тяжести mg и сила со стороны электрического поля, где
—начальный заряд пылинки и E1 = V1/d—напряженность электрического поля в конденсаторе.
Чтобы пылинка могла находиться в равновесии, верхняя пластина конденсатора должна быть заряжена отрицательно. При равновесии
mg = F, или ; отсюда
.
Так как уменьшение заряда пылинки на qo=1000e равносильно увеличению положительного заряда на qo, то новый заряд пылинки q2 = q1+qo. При равновесии , где V2—новая разность потенциалов между пластинами. Учитывая выражения для q2, q1 и q0, найдем
Таким образом, разность потенциалов нужно изменить на V2— V1 = — 980 В (знак минус показывает, что ее нужно уменьшить, так как заряд пылинки увеличился).
24 Решить предыдущую задачу, считая пылинку заряженной отрицательно.
Решение:
Верхняя пластина конденсатора должна быть заряжена положительно. Новый заряд пылинки q2 = q1-qo, где qo=1000e.
Поэтому (см. задачу 23)
Напряжение между пластинами нужно увеличить на V2— V1 = 1460 В.
25 В электрическое поле плоского конденсатора, пластины которого расположены горизонтально, помещена капелька масла, имеющая заряд q=1 е. Напряженность электрического поля подобрана так, что капелька покоится. Разность потенциалов между пластинами конденсатора V =500 В, расстояние между пластинами d=0,5 см. Плотность масла . Найти радиус капельки масла.
Решение:
При равновесии откуда
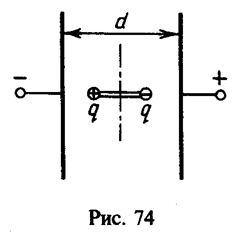
26 Внутри плоского конденсатора, пластины которого расположены вертикально, помещена диэлектрическая палочка длины l=1 см с металлическими шариками на концах, несущими заряды +q и — q(|q|=1 нКл). Палочка может вращаться без трения вокруг вертикальной оси, проходящей через ее середину. Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=10см. Какую работу необходимо совершить, чтобы повернуть палочку вокруг оси на 180° по отношению к тому положению, которое она занимает на рис. 74?
Решение:
Напряженность электрического поля в конденсаторе E=V/d.
Разность потенциалов между точками, где расположены заряды,
где —потенциал в точке расположения заряда + q, а
—потенциал в точке расположения заряда — q; при этом
. При повороте палочки электрические силы совершают работу по переносу заряда — q из точки а в точку b и заряда + q из точки b в точку а, равную
Знак минус означает, что работу должны совершить внешние силы.
27 Внутри плоского конденсатора помещен диэлектрический стержень длины l=3 см, на концах которого имеются два точечных заряда + q и —q (|q|=8нКл). Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=8 см. Стержень ориентирован параллельно пластинам. Найти момент сил, действующий на стержень с зарядами.
Решение:
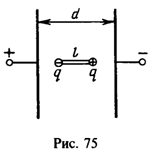
28 На концах диэлектрической палочки длины l=0,5 см прикреплены два маленьких шарика, несущих заряды — q и +q (|q|=10 нКл). Палочка находится между пластинами конденсатора, расстояние между которыми d=10cм (рис.75). При какой минимальной разности потенциалов между пластинами конденсатора V палочка разорвется, если она выдерживает максимальную силу растяжения F=0,01 Н? Силой тяжести пренебречь.
Решение:
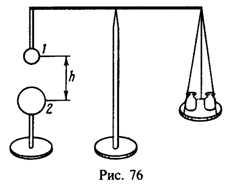
29 Металлический шарик 1 радиуса R1=1 см прикреплен с помощью диэлектрической палочки к коромыслу весов, после чего весы уравновешены гирями (рис. 76). Под шариком 1 помещают заряженный шарик 2 радиуса R2=2 см. Расстояние между шариками h = 20 см. Шарики 1 и 2 замыкают между собой проволочкой, а потом проволочку убирают. После этого оказывается, что для восстановления равновесия надо снять с чашки весов гирю массы m = 4мг. До какого потенциала j был заряжен шарик 2 до замыкания его проволочкой с шариком 1?
Решение:
Если до замыкания шарик 2 имел заряд 0, то сумма зарядов шариков 1 и 2 после замыкания q1+q2 = q. Потенциалы же их после замыкания одинаковы: . Следовательно,
После замыкания шарик 2 действует на шарик 1 с силой
откуда
Начальный потенциал шарика 2
Любые заряженные тела создают вокруг себя электростатическое поле. Рассмотрим особенности электростатического поля, создаваемого точечным зарядом и заряженной сферой.
Электростатическое поле точечного заряда
Направление силовых линий электростатического поля точечного заряда
Модуль напряженности не зависит от значения пробного заряда q0:
E=FKq0=kQq0r2q0=kQr2
Модуль напряженности точечного заряда в вакууме:
E=kQr2
Модуль напряженности точечного заряда в среде:
E=kQεr2
Сила Кулона:
−FKулона=q−E
Потенциал не зависит от значения пробного заряда q0:
φ=Wpqo=±kQq0rq0=±kQr
Потенциал точечного заряда в вакууме:
φ=±kQr
Потенциал точечного заряда в среде:
φ=±kQεr
Внимание! Знак потенциала зависит только от знака заряда, создающего поле.
Эквипотенциальные поверхности для данного случая — концентрические сферы, центр которых совпадает с положением заряда.
Работа электрического поля по перемещению точечного заряда:
A12=±q(φ1−φ2)
Пример №1. Во сколько раз увеличится модуль напряженности электрического поля, созданного точечным зарядом Q в некоторой точке, при увеличении значения этого заряда в 5 раз?
Модуль напряженности электрического поля, созданного точечным зарядом, определяется формулой:
E=kQεr2
Формула показывает, что модуль напряженности и электрический заряд — прямо пропорциональные величины. Следовательно, если заряд, который создает поле, увеличится в 5 раз, то модуль напряженности создаваемого поля тоже увеличится в 5 раз.
Электростатическое поле заряженной сферы
Направление силовых линий электростатического поля заряженной сферы:
Модуль напряженности электростатического поля заряженной сферы:
| Внутри проводника (расстояние меньше радиуса сферы, или r < R) |
E=0 |
| На поверхности проводника (расстояние равно радиусу сферы, или r = R) |
E=kQR2 |
| Вне проводника (расстояние больше радиуса сферы, или r > R) |
E=kQr2=kQ(R+a)2 a — расстояние от поверхности сферы до изучаемой точки. r — расстояние от центра сферы до изучаемой точки. |
Сила Кулона:
−FK=q−E
Потенциал:
| Внутри проводника и на его поверхности (r < R или r = R) |
φ=±kQR |
| Вне проводника (r > R) |
φ=±kQr=±φ=±kQR+a |
Пример №2. Определить потенциал электростатического поля, создаваемого заряженной сферой радиусом 0,1 м, в точке, находящейся на расстоянии 0,2 м от этой сферы. Сфера заряжена положительна и имеет заряд, равный 6 нКл.
6 нКл = 6∙10–9 Кл
Так как сфера заряжена положительно, то потенциал тоже положителен:
Задание EF18107
Два неподвижных точечных заряда действуют друг на друга с силами, модуль которых равен F. Чему станет равен модуль этих сил, если один заряд увеличить в n раз, другой заряд уменьшить в n раз, а расстояние между ними оставить прежним?
Ответ:
а) F
б) nF
в) Fn
г) n2F
Алгоритм решения
1.Записать исходные данные.
3.Применить закон Кулона к обоим зарядам для 1 и 2 случая.
4.Установить, как меняется сила, с которой заряды действуют друг на друга.
Решение
Запишем исходные данные:
• Первая пара зарядов: q1 и q2.
• Вторая пара зарядов: q1’ = nq1 и q2’=q2/n.
• Расстояние между зарядами: r1 = r2 = r.
Закон Кулона:
FK=k|q1||q2|r2
Применим закон Кулона к парам зарядов. Закон Кулона для первой пары:
FK1=k|q1||q2|r2
Закон Кулона для второй пары:
FK2=k|nq1|∣∣q2n∣∣r2=k|q1||q2|r2
Коэффициент n сократился. Следовательно, силы, с которыми заряды взаимодействуют друг с другом, не изменятся:
FK1=FK2
После изменения зарядов модуль силы взаимодействия между ними останется равным F.
pазбирался: Алиса Никитина | обсудить разбор
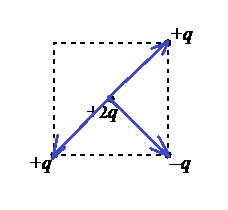
Задание EF18591
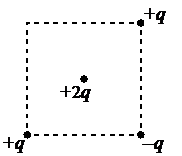
Ответ:
а) ↘
б) →
в) ↖
г) ↓
Алгоритм решения
1.Сделать чертеж. Обозначить все силы, действующие на центральный точечный заряд со стороны остальных точечных зарядов.
2.Найти равнодействующую сил геометрическим способом.
Решение
Сделаем чертеж. В центр помещен положительный заряд. Он будет отталкиваться от положительных зарядов и притягиваться к отрицательным:
Модули всех векторов сил, приложенных к центральному точечному заряду равны, так как модули точечных зарядов, расположенных в вершинах квадрата равны, и находятся они на одинаковом расстоянии от этого заряда.
Складывая векторы геометрически, мы увидим, что силы, с которыми заряд +2q отталкивается от точечных зарядов +q, компенсируют друг друга. Поэтому на заряд действует равнодействующая сила, равная силе, с которой он притягивается к отрицательному точечному заряду –q. Эта сила направлена в ту же сторону (к нижней правой вершине квадрата).
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22574
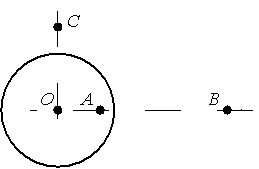
Установите соответствие между физическими величинами и их значениями.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать формулы для нахождения напряженности электростатического поля внутри и снаружи заряженной сферы.
2.Определить величину напряженности поля в указанных точках.
3.Установить соответствие между величинами и их значениями.
Решение
Внутри заряженной сферы напряженность электростатического поля равна 0. Поэтому напряженность в точке А равна 0.
EA=0
Снаружи заряженной сферы напряженность электростатического поля равна:
E=kQr2=kQ(R+a)2
Найдем напряженность электростатического поля в точке В, которая находится на расстоянии 3R от центра заряженной сферы:
EB=kQr2=kQ(3R)2=kQ9R2
Чтобы выразить EB через Eс, найдем напряженность электростатического поля в точке С, которая находится на расстоянии 3R/2 от центра заряженной сферы:
EС=kQr2=kQ(32R)2=4kQ9R2
Найдем отношение EB к Eс:
EBEС=kQ9R2÷4kQ9R2=kQ9R2·9R24kQ=14
Следовательно:
EB=EС4
Ответ: 14
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 7.5k