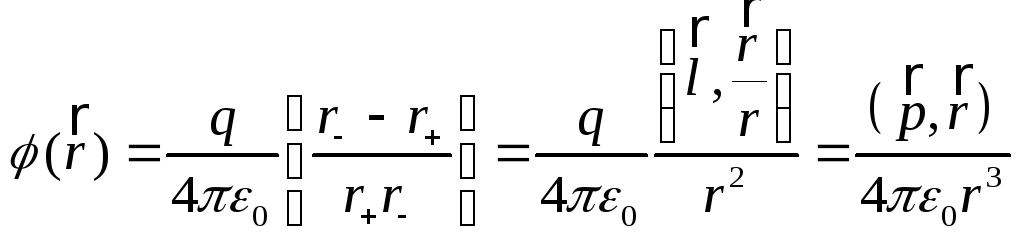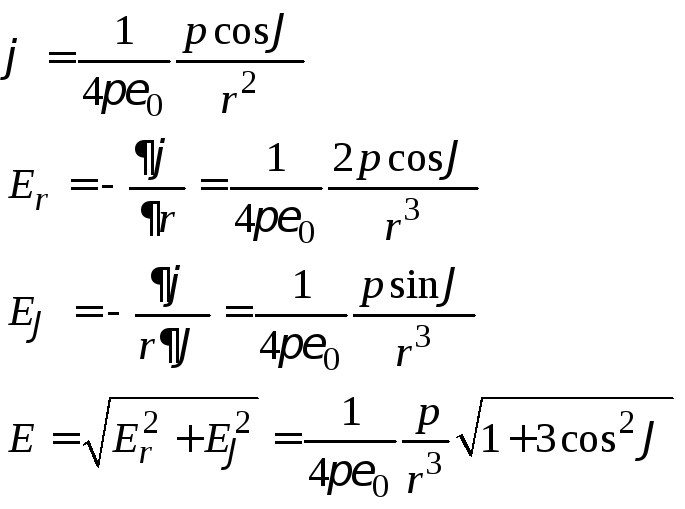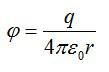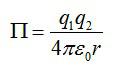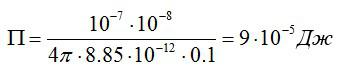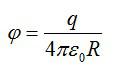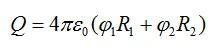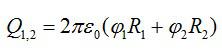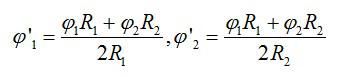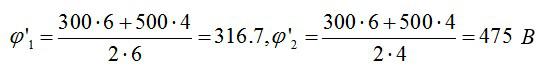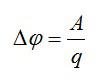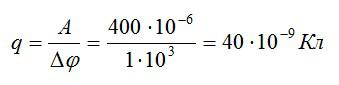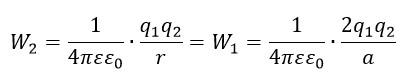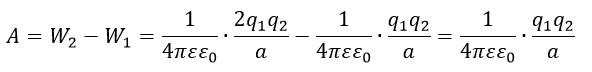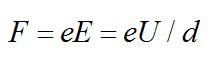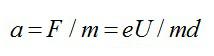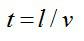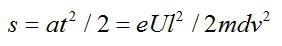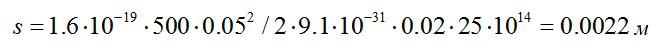Как найти потенциал пример

Рассмотрим
вычисление потенциала поля, созданного
некоторыми заряженными телами.

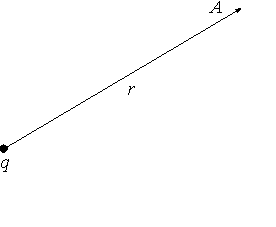
Рис.3.
Расположение точки наблюдения А по
отношению к точечному источнику поля
q

1.
Пример
Точечный
заряд.
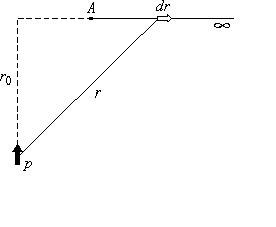
Используя соотношения (1) и (4) и совмещая
точку 1 с точкой наблюдения А
(рис.3), а точку 2 удаляя на бесконечность,
получим

(7)

Замечание.
До сих пор использовалось понятие
векторного поля — поля векторов
(каждой точке пространства ставится в
соответствие вектор).
Представление о потенциале
как
функции точки пространства позволяет
ввести понятие скалярного поля — поля
чисел

(каждой точке пространства ставится в
соответствие, с точностью до произвольной
аддитивной постоянной, число
).
Поэтому в дальнейшем кроме понятий
электростатическое поле и поле
,
будем использовать понятие поля.

2.Пример. Найдем потенциал бесконечной однородно заряженной с линейной плотностью нити.

Наша задача найти

как функцию
.

Как
уже было показано для бесконечно длинной
нити:.

Выберем где-нибудь
точку из которой мы стартуем, к примеру
в точке
,
то

.

Договоримся, что
в точке старта потенциал равен нулю:
,
тогда

.

Это при такой
нормировке. Если в такой задаче нормировать

,
то получим,то
есть все потенциалы во всех точках
бесконечно большие. Кому нужна такая
нормировка? Если Вас интересует какой-то
конкретный пространственный диапазон,
то нормировать надо где-то вблизи этой
области, тогда все потенциалами будут
конечными приятными числами. От
бесконечной нити нельзя уйти на
бесконечность, по этой же причине не
следует ожидать хорошего результата
откак суммы потенциалов точечных фрагментов
нити, каждый из которых нормирован
условием.

3.Пример. Потенциал поля точечного диполя (первый способ).

Итак,
мы рассматриваем точечный диполь и
точку наблюдения достаточно далеко от
этой нашей гантельки.

Давайте искать
потенциал этой точки наблюдения.

Во первых, принцип
суперпозиции.

Во-вторых, как
известно

.

Учтя, что
есть проекция векторанаи то, что расстояние до диполя очень
велико, то

Потенциал поля точечного диполя (второй способ).

Используем готовую
формулу для напряженности поля:

.
Вот такое выражение мы с вами в свое
время вывели. Обопремся на него.

Д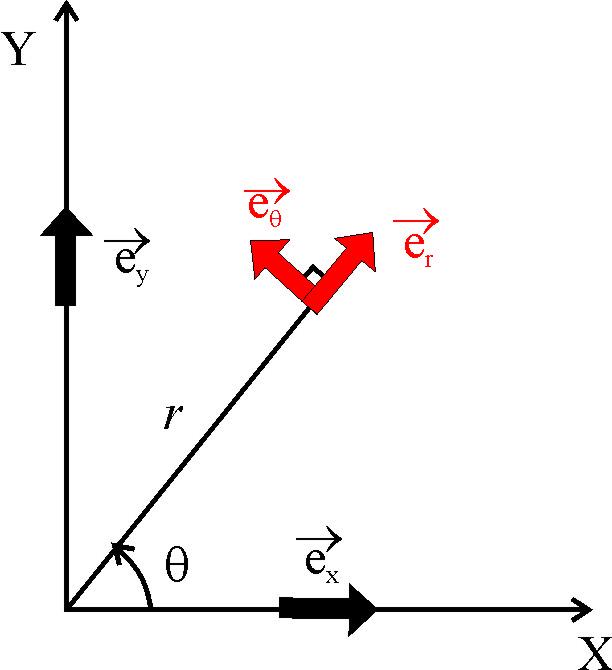авайте
выберем такое направление, чтобы нам
было удобно вычислять этот интеграл,
так как поле потенциальное, то результат
не будет зависеть от вида траектории.
Ориентация диполя, направление движения
и векторпоказаны
на рисунке. С учетом некоторых соотношений
(5) примет вид:

Определение
вектора
точечного
диполя из
в
полярной системе координат.

Оператор
запишется в полярной системе координат
так:

Ортыкоординатных
осей декартовой и полярной систем
координат (см.рис.)

4.Пример

См. Иродов задача
3.38. (часть2)

Показать, что
потенциал диполя с электрическим
моментом может быть представлен как,
где–радиус
вектор. Найти с помощью этого выражения
модуль напряженности электрического
поля диполя как функциюи.

—
это уже показали выше, отсюда, раскрывая
скалярное произведение и продифференцировав
формулу для потенциала, мы получим
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Физические задачи по электростатике мало кто любит. Но что поделать, решать их надо. Разберемся, как это делать по-быстрому и с использованием подробных примеров решений задач на разность потенциалов, задач на работу электрического поля и напряженность.

Наш телеграм – полезная информация для абитуриентов и студентов всех специальностей, присоединяйтесь!

Решение задач на разность потенциалов и работу поля: примеры

Задача №1 на потенциальную энергию системы зарядов

Условие

Два точечных заряда величиной 100 нКл и 10 нКл находятся на расстоянии r=10 см друг от друга. Вычислить потенциальную энергию системы этих зарядов.

Решение

Потенциал поля точечного заряда равен:

Так что, потенциальная энергия зарядов будет равна:

Подставим значения из условия и найдем:

Ответ: П=9*10^-5 Дж.

Задача №2 на определение потенциала заряженных шаров

Условие

Шар радиусом R1=6 см заряжен до потенциала 300 В , а шар радиусом R2=4 см – до потенциала 500 В. Найдите потенциал шаров после того, как их соединили металлическим проводом, емкостью которого можно пренебречь.

Решение

Потенциал шара равен:

Суммарный заряд двух шаров будет равен:

После соединения шаров заряд каждого будет равен:

Тогда суммарный потенциал шаров вычислится по формуле:

Подставим значения и найдем:  

Ответ: 317 В; 475 В.

Задача №3 на разность потенциалов и работу по перемещению заряда

Условие

Заряд переместился между двумя точками с разностью потенциалов 1 кВ, при этом поле совершило работу, равную 40 мкДж. Найдите величину заряда.

Решение

По определению, разность потенциалов равна работе по перемещению заряда, деленной на величину этого заряда:

Отсюда можно выразить заряд и вычислить ответ:

Ответ: 40 нКл.

Задача №4 на работу электрического поля по перемещению заряда

Условие

Два точечных заряда q1=6 мкКл  и  q2=2 мкКл, находятся на расстоянии а=60 см друг от друга. Какую работу необходимо свершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?

Решение

Находясь на расстоянии a, точечные заряды обладали потенциальной энергией:

На вдвое меньшем расстоянии энергия зарядов равна:

Работа, затраченная на сближение зарядов:

Подставляем числовые данные и вычисляем:

Ответ: A=0,18 Дж.

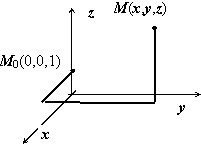
Задача №5 на движение заряженной частицы в поле

Условие

Электрон влетает в плоский воздушный конденсатор параллельно его пластинам со скоростью V=5·107 м/с. Расстояние между пластинами d=2 см, разность потенциалов U=500 В. Найти отклонение электрона, вызванное полем конденсатора, если длина его пластины l=5 см.

Решение

При движении в электрическом поле конденсатора на электрон действует сила:

Ускорение электрона, по 2 закону Ньютона, определяется формулой:

Время движения электрона в конденсаторе вычислим, зная длину пластины и скорость частицы:

Отклонение электрона будет равно:

Найдем:

Ответ: 2.2 мм

Вопросы на тему «Работа электрического поля и разность потенциалов»

Вопрос 1. Что такое потенциал электрического поля?

Ответ. Потенциал – скалярная физическая величина, являющаяся энергетической характеристикой электростатического поля.

Потенциал поля равен отношению потенциальной энергии поля (или работы по перемещению заряда из данной точки на нулевой уровень потенциальной энергии) к величине заряда.

Для потенциала применим принцип суперпозиции.

Вопрос 2. Что такое разность потенциалов?

Ответ. Разность потенциалов – это работа по перемещению заряда из одной точки в другую. Разность потенциалов еще называют напряжением, обозначая его как разность потенциалов в начальной и конечной точках траектории заряда.

Вопрос 3. Что происходит с зарядом, когда он попадает в электрическое поле?

Ответ. На заряд со стороны поля действует сила, способная перемещать заряд в поле и совершать работу.

Вопрос 4. Какую природу имеет сила, действующая на заряд? Зависит ли величина работы от траектории заряда в поле?

Ответ. Сила, действующая со стороны поля на заряд, является проявлением электромагнитного взаимодействия. Величина работы поля не зависит от траектории заряда, так как это работа потенциальных (консервативных) сил.

Для наилучшего понимания сути задач на потенциал и работу поля, можно провести параллель между работой по перемещению заряда, потенциальной энергией в механике и работой силы тяжести.

Вопрос 5. Что такое эквипотенциальная поверхность?

Ответ. Это поверхность, во всех точках которой потенциал электрического поля имеет одинаковое значения.

Какие бы задачи вы не решали и где ни учились, профессиональный образовательный сервис для студентов готов оказать помощь с проблемами по учебе любой сложности.

Потенциал. Разность потенциалов. ЗАДАЧИ с решениями

Формулы, используемые на уроках «Решение задач на тему: Работа перемещения заряда в электрическом поле. Потенциал. Разность потенциалов» для подготовки к ЕГЭ.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
 Металлический шар диаметром d заряжен с поверхностной плотностью зарядов σ. Найти потенциал φ этого шара, если он окружен заземленной проводящей сферой, имеющей общий с шаром центр. Диаметр сферы D. Среда — воздух.

Задача № 2.
 Потенциал заряженного шара φ₁ = 300 В. Чему равен потенциал φ₂ электрического поля этого шара в точке, отстоящей на расстоянии l = 50 см от его поверхности, если радиус шара R = 25 см?

Задача № 3.
 Определить потенциал φ точки поля, находящейся на расстоянии а =  9 см от поверхности заряженного шара радиусом R = 1 см, если поверхностная плотность зарядов на шаре σ = 1 • 10^–11 Кл/см². Среда — воздух.

Задача № 4.
 В точке 1 поля точечного заряда-источника потенциал φ₁ = 40 В, а в точке 2 φ₂ = 10 В. Найти потенциал φ в точке М, лежащей посередине между точками 1 и 2 (рис. 3-6). 

Задача № 5.
 В трех вершинах квадрата со стороной а = 20 см находятся заряды q₁ = 1 • 10^–8 Кл, q₂ = 2 • 10^–8 Кл и q₃ = 2 • 10^–8 Кл (рис. 3-7). Определить потенциал φ электрического поля, созданного этими зарядами в четвертой вершине. 

Задача № 6.
 Четыре одинаковых точечных заряда q расположены на одной прямой на расстоянии r друг от друга. Какую работу А надо совершить, чтобы переместить эти заряды в вершины тетраэдра со стороной r? Среда — вакуум.

Задача № 7.
Два одинаково заряженных шарика диаметрами d = 0,5 см каждый расположены на расстоянии l = 2 см между их поверхностями (рис. 3-14). До какого потенциала φ они заряжены, если сила их отталкивания друг от друга F = 2 мкН? Среда — воздух. 

Задача № 8.
 В однородном электрическом поле напряженностью Е = 2 кВ/см переместили заряд q = –20 нКл в направлении силовой линии поля на расстояние d = 10 см. Найти работу поля А, изменение потенциальной энергии поля ΔW_п и напряжение (разность потенциалов) U между начальной и конечной точками перемещения.

Задача № 9.
 Между двумя горизонтальными плоскостями, заряженными разноименно и расположенными на расстоянии d = 5 мм друг от друга, находится в равновесии капелька масла массой 20 нг (нанограмм) (рис. 3-10). Найти число избыточных электронов N на этой капельке. Среда — воздух. Разность потенциалов между плоскостями U = 2 кВ. 

Задача № 10.
 На пластине М поддерживается потенциал φ₁ = +80 В, а на пластине N – φ₂ = –80 В (рис. 3-11, а). Расстояние между пластинами d = 10 см. На расстоянии d₁ = 4 см от пластины М помещают заземленную пластину Р (рис. 3-11, б). Найти изменение напряженности ΔЕ₁ поля на участке МР и изменение напряженности поля ΔЕ₂ на участке PN при этом. Построить графики зависимостей напряженностей Е = Е(х) и потенциала φ = φ(х) от расстояния между точками поля и пластинами. 

Это конспект по теме «Потенциал. Разность потенциалов. ЗАДАЧИ с решениями». Выберите дальнейшие действия:

• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

Нахождение потенциала

В предыдущем разделе мы доказали, что если выполняются условия потенциальности поля $bar { a } (mathbf { textit { M } } )$, то $varphi (M)=intlimits_ { mathop { M_0 M } limits^cup } { bar { a } dbar { r } } $, где $M_0 in V$ — фиксированная точка. Обычно, если в точке $mathbf { textit { O } } (0,0,0)$ поле не имеет особенностей, то в качестве точки $M_0 (x_0 ,y_0 ,z_0 )$ берётся именно эта точка, если в этой точке поле не определено, берётся другая точка.

Интегрирование ведут по пути, состоящим из отрезков, параллельных координатным осям. В результате получим $varphi (M)=intlimits_ { x_0 } ^x { P(x,y_0 ,z_0 )dx } +intlimits_ { y_0 } ^y { Q(x,y,z_0 )dy } +intlimits_ { z_0 } ^z { R(x,y,z)dz } $.

Пример 1

Доказать, что поле $bar { a } (x,y,z)=frac { ycos (xy) } { z } bar { i } +frac { xcos (xy) } { z } bar { j } -frac { sin (xy) } { z^2 } bar { k } $ потенциально и найти потенциал этого поля.

Решение

Мы будем доказывать, что это поле потенциально в любой односвязной области $mathbf { textit { V } } $, не содержащей точку $mathbf { textit { O } } (0,0,0)$. Условие безвихревости поля $bar { a } $:

$rotbar { a } (M)=left| { begin{array} { l } ,bar { i } ,,,,bar { j } ,,,bar { k } \ frac { partial } { partial x } ,,frac { partial } { partial y } ,,frac { partial } { partial z } \ ,P,,Q,,,R \ end{array} }right|=left( { frac { partial R } { partial y } -frac { partial Q } { partial z } }right)bar { i } +left( { frac { partial P } { partial z } -frac { partial R } { partial x } }right)bar { j } +left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)bar { k } =0$ в координатной форме сводится к равенствам $frac { partial R } { partial y } =frac { partial Q } { partial z } , frac { partial P } { partial z } =frac { partial R } { partial x } , frac { partial Q } { partial x } =frac { partial P } { partial y } $.

В нашем поле $P(x,y,z)=frac { ycos (xy) } { z } , Q(x,y,z)=frac { xcos (xy) } { z } ,R(x,y,z)=-frac { sin (xy) } { z^2 } $. Находим производные:

$frac { partial R } { partial y } =-frac { xcos (xy) } { z^2 } $,

$frac { partial Q } { partial z } =-frac { xcos (xy) } { z^2 } =frac { partial R } { partial y } $,

$frac { partial P } { partial z } =-frac { ycos (xy) } { z^2 } $,

$frac { partial R } { partial x } =-frac { ycos (xy) } { z^2 } =frac { partial P } { partial z } $,

$frac { partial Q } { partial x } =frac { cos (xy)-xysin (xy) } { z } $,

$frac { partial P } { partial y } =frac { cos (xy)-xysin (xy) } { z } =frac { partial Q } { partial x } $ Потенциальность поля доказана.

Ищем потенциал. Интеграл $varphi (M)=intlimits_ { mathop { M_0 M } limits^cup } { bar { a } dbar { r } } $ вычисляем по изображённому на рисунке пути, отправляясь от точки $mathbf { textit { M } } _ { 0 } $(0,0,1). $varphi (x,y,z)=intlimits_0^x { frac { 0cdot cos (xcdot 0) } { 1 } dx } +intlimits_0^y { frac { xcdot cos (xy) } { 1 } dy } -intlimits_1^z { frac { sin (xy) } { z^2 } dz } = =left. { sin (xy) }right|_0^y +left. { frac { sin (xy) } { z } }right|_1^z =sin (xy)+left[ { frac { sin (xy) } { z } -sin (xy) }right]=frac { sin (xy) } { z } $.

Если бы мы взяли в качестве точки $mathbf { textit { M } } _ { 0 } $ другую точку $mathbf { textit { M } } _ { 1 } $, то получили бы выражение, отличающееся на некоторую постоянную { более точно, на $C=intlimits_ { mathop { M_0 M_1 } limits^cup } { bar { a } dbar { r } } )$, поэтому $varphi (x,y,z)= frac { sin (xy) } { z } +C$.