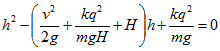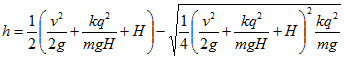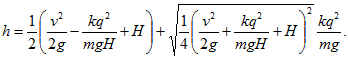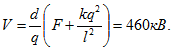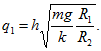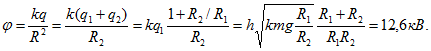Как найти потенциал капли ртути

Разберем сегодня несколько задач по физике, связанных с вычислением потенциала сферы. Так уж сложилось, что новые задачи по физике появляются значительно реже, нежели, к примеру скажем, по математике. Оно и понятно, ведь придумать оригинальную физическую задачу далеко не просто. Из года в год в различных физических олимпиадах, вариантах ЕГЭ по физике и других диагностических работах появляются одни и те же задачи, причем зачастую авторы по разным причинам не меняют даже числовых значений входящих в условие параметров. Решение некоторых таких часто встречающихся (напрашивается назвать их «бородатыми», но мы назовем их лучше «популярными») задач приведено в данной статье.

Задача 1. В одну большую каплю сливают n одинаковых капелек ртути, заряженных до потенциала φ. Каков будет потенциал Φ этой капли? Считать, что капли имеют сферическую форму.

Решение. Потенциал заряженного шара (коим по условию является каждая из капель) определяется по формуле:

где Q — заряд шара, ε₀ = 8,85 · 10^-12 Ф/м — диэлектрическая постоянная, R — радиус шара.

Тогда потенциал образовавшейся после слияния капли можно определить так:

Общий заряд Q, по закону сохранения заряда, определяется суммой зарядов q каждой маленькой капли: Q = n · q. Как связать радиус R получившейся большой капли с радиусом r каждой малой? Используем то, что в результате слияния не изменяется объем ртути, то есть (предполагается, что вы помните формулу для вычисления объема шара, если нет — загляните сюда):

Итак, получаем:

Но

есть по определению потенциал одной маленькой капли, поэтому окончательно получаем ответ:

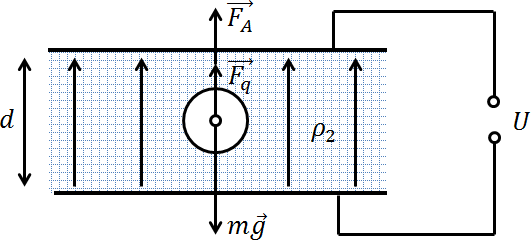
Задача 2. Металлический шар радиусом r помещен в жидкий диэлектрик с плотностью ρ₂. Плотность материала, из которого изготовлен шар, ρ₁ (ρ₁ > ρ₂). Чему равен заряд шара, если в однородном электрическом поле, направленном вертикально вверх, шар оказался взвешенным в жидкости? Электрическое поле создается двумя параллельными пластинами, расстояние между которыми d, а разность потенциалов U.

Решение.

На шар действуют три силы: сила тяжести mg = ρ₁gV (направлена вниз), выталкивающая сила Архимеда F_A = ρ₂gV (направлена вверх), сила Кулона F_q = qE (направлена вверх). То, что сила Кулона направлена вверх следует из того, что плотность материала шара больше плотности жидкого диэлектрика, в котором он плавает. Это означает, что он утонул бы, не будь он заряжен. Спасает его от этого дополнительная сила Кулона, сонаправленная с выталкивающей силой Архимеда.

Шар находится в равновесии, значит векторная сумма всех действующих на него сил равна нулю:

Или в проекции на вертикальную ось:

С учетом написанных выше формул:

С учетом формулы для объема шара (V = 4/3πr³) и формулы, отражающей взаимосвязь напряженности поля с напряжением между двумя точками (U=E·d), получаем окончательный ответ:

Задача 3. Проводник длиной l движется с постоянным ускорением a, направленным вдоль его оси. Определите напряжение, возникающее между концами проводника; m_e — масса электрона, |e| — элементарный заряд.

Решение. В процессе движения стержня часть электронов по инерции смещается к одному из его концов (ситуация напоминает поезд в метро — стержень — и едущих в нем пассажиров — электроны).

Процесс перетекания будет продолжаться до тех пор, пока возникшее в стержне электрическое поле не начнет действовать на электроны с силой |e|E, где E — напряженность этого поля, равной по величине m_ea. Напряженность поля связана с напряжением между концами проводника соотношением: U = E · l. После всех подстановок и преобразований получает ответ:

Задачи взяты из сборника В. И. Васюкова, С. Н. Дмитриева, Ю. А. Струкова «Физика: сборник задач для поступающих в вузы». Все задания в этом сборнике приведены с ответами, поэтому при желании вы можете самостоятельно оценить свои силы в их решении. Присылайте свои вопросы и интересные задачи, и мы обязательно разберем их в одной из следующих статей.

Репетитор по физике на Юго-Западной
Сергей Валерьевич

2017-08-20   

Капля ртути, заряженная до потенциала $phi_{0}$, распадается на $N$ одинаковых капель с одинаковыми зарядами. Капли разлетаются на большое расстояние друг от друга. Определите потенциал $phi$ каждой из образовавшихся капель.

Решение:

Потенциал заряженной капли (проводящего шара) $phi_{0} = k frac{Q}{R}$, заряд каждой, из маленьких капель $q = frac{Q}{N}$. Радиус $r$ маленьких капель найдем из условия неизменности объема ртути:

$frac{4 pi R^{3}}{3} = N frac{4 pi r^{3}}{3}$,

откуда $r = frac{R}{N^{1/3}}$. Тогда потенциал образовавшихся капель составит $phi = k frac{q}{r} =k frac{Q}{N^{2/3}R} = frac{ phi_{0}}{N^{2/5}}$, т. е. уменьшается. Отметим, что этот ответ справедлив только в том случае, когда образовавшиеся капли разлетятся на большое расстояние (чтобы можно было пренебречь энергией их взаимодействия).

Ответ: $phi = frac{ phi_{0}}{ N^{2/3}}$.

Условие задачи:

Тысяча одинаковых шарообразных капелек ртути заряжены до одинакового потенциала 0,1 В. Определите потенциал большой шарообразной капли, получившейся в результате слияния малых капель.

Задача №6.4.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(N=1000), (varphi_0=0,1) В, (varphi-?)

Решение задачи:

Вы должны понимать, что объем большой шарообразной капли (V) равен сумме объемов (V_0) всех маленьких капелек ртути, которых согласно условию всего (N) штук. Поэтому имеет место равенство:

[V = N{V_0};;;(1)]

Пусть радиус большой капли равен (R), радиус маленьких капелек – (r), тогда, вспомнив формулу из математики для определения объема шара, можно записать формулу (1) в следующем виде:

[frac{4}{3}pi {R^3} = N cdot frac{4}{3}pi {r^3}]

[{R^3} = N{r^3}]

Откуда:

[frac{R}{r} = {N^{frac{1}{3}}};;;(2)]

Запишем формулы для определения электроемкостей большой (C) и маленьких (C_0) капель:

[left{ begin{gathered}
C = 4pi {varepsilon _0}R hfill \
{C_0} = 4pi {varepsilon _0}r hfill \
end{gathered} right.]

Поделим верхнее равенство на нижнее:

[frac{C}{{{C_0}}} = frac{R}{r}]

Если учесть ранее полученное (2), имеем:

[frac{C}{{{C_0}}} = {N^{frac{1}{3}}};;;(3)]

Из закона сохранения заряда следует, что между зарядом большой капли (q) и зарядами (q_0) капель в количестве (N) штук существует соотношение:

[q = N{q_0}]

[frac{q}{{{q_0}}} = N;;;(4)]

Запишем формулы для определения потенциалов большой (varphi) и маленьких (varphi_0) капель через заряды и электроемкости:

[left{ begin{gathered}
varphi = frac{q}{C} hfill \
{varphi _0} = frac{{{q_0}}}{{{C_0}}} hfill \
end{gathered} right.]

Поделим верхнее равенство на нижнее, тогда:

[frac{varphi }{{{varphi _0}}} = frac{{q cdot {C_0}}}{{{q_0} cdot C}}]

Учитывая (3) и (4), получим:

[frac{varphi }{{{varphi _0}}} = frac{N}{{{N^{frac{1}{3}}}}}]

[varphi = {varphi _0}{N^{frac{2}{3}}}]

Задача решена в общем виде, считаем ответ:

[varphi = 0,1 cdot {1000^{frac{2}{3}}} = 10;В]

Ответ: 10 В.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.4.5 Проводники, заряженные одинаковым зарядом, имеют потенциалы 40 и 60 В
6.4.7 Шар радиусом 15 см, заряженный до потенциала 300 В, соединяют проволокой
6.4.8 Шарообразная капля, имеющая потенциал 2,5 В, получена в результате слияния двух

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Решение:


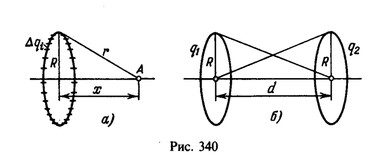
15 Два параллельных тонких кольца радиуса R расположены на расстоянии d друг от друга на одной оси. Найти работу электрических сил при перемещении заряда q_o из центра первого кольца в центр второго, если на первом кольце равномерно распределен заряд q₁, а на втором — заряд q₂.

Решение:

Найдем потенциал, создаваемый зарядом q, находящимся на кольце, в точке А на оси кольца, расположенной на расстоянии
х от его центра (рис. 340, а) и, следовательно, на расстояниях от точек, лежащих на кольце. Разобьем кольцо на отрезки, малые по сравнению с расстоянием r. Тогда заряд , находящийся на каждом отрезке (i — номер отрезка), можно рассматривать как точечный. Он создает в точке А потенциал . Потенциал, создаваемый в точке А всеми отрезками кольца (отстоящими от этой точки на одно и то же расстояние r), будет

В скобках стоит сумма зарядов всех отрезков, т. е. заряд всего кольца q; поэтому

Потенциал Ф₁ поля в центре первого кольца складывается из потенциала, создаваемого зарядом q₁, находящимся на первом кольце, для которого х=0, и потенциала, создаваемого зарядом q₂, находящимся на втором кольце, для которого x=d (рис. 340, б). Аналогично находится потенциал в центре второго кольца:

Окончательно для работы имеем

16 На тонком кольце радиуса R равномерно распределен заряд q. Какова наименьшая скорость υ, которую необходимо сообщить находящемуся в центре кольца шарику массы т с зарядом q_o, чтобы он мог удалиться от кольца в бесконечность?

Решение:
Если заряды q_o и q одного знака, то удалить шарик от кольца в бесконечность можно, сообщив ему бесконечно малую скорость. Если же знаки зарядов разные, то сумма кинетической и потенциальной энергий шарика в центре кольца должна быть равна нулю, так как она равна нулю в бесконечности: , где φ=kq/R — потенциал в центре кольца (см. задачу 17); отсюда

17 На шарик радиуса R=2 см помещен заряд q=4 пКл. С какой скоростью подлетает к шарику электрон, начавший движение из бесконечно удаленной от него точки?

Решение:


18 Между горизонтально расположенными пластинами плоского конденсатора с высоты Н свободно падает незаряженный металлический шарик массы т. На какую высоту h после абсолютно упругого удара о нижнюю пластину поднимется шарик, если в момент удара на него переходит заряд q? Разность потенциалов между пластинами конденсатора равна V, расстояние между пластинами равно d.

Решение:
Внутри конденсатора имеется однородное электрическое поле с напряженностью Е= V/d, направленной вертикально. После удара шарик приобретает заряд того же знака, что и нижняя пластина конденсатора. Поэтому на него будет действовать со стороны электрического поля сила F=qE=qV/d, направленная вверх. Согласно закону сохранения энергии изменение энергии равно работе внешних сил (в данном случае — электрических). Учитывая, что удар абсолютно упругий и что в начальный и конечный моменты шарик имеет лишь потенциальную энергию в поле силы тяжести, получим
откуда

19 Два шарика с одинаковыми зарядами q расположены на одной вертикали на расстоянии Н друг от друга. Нижний шарик закреплен неподвижно, а верхний, имеющий массу m, получает начальную скорость v, направленную вниз. На какое минимальное расстояние h приблизится верхний шарик к нижнему?

Решение:
Согласно закону сохранения энергии

где qV—работа электрических сил, V=kq/H—kq/h — разность потенциалов точек начального и конечного положения верхнего шарика. Для определения h получаем квадратное уравнение:

Решая его, найдем

(знак плюс перед корнем соответствовал бы максимальной высоте, достигнутой шариком, если бы он получил ту же начальную скорость, направленную вверх).

20 Найти максимальное расстояние h между шариками в условиях предыдущей задачи, если неподвижный шарик имеет отрицательный заряд q, а начальная скорость v верхнего шарика направлена вверх.

Решение:


21 Электрон, пролетая в электрическом поле путь от точки а к точке b, увеличил свою скорость с ν_a=1000 км/с до ν_ab = 3000 км/с. Найти разность потенциалов между точками а и b электрического поля.

Решение:
Работа, совершенная над электроном электрическим полем, идет на увеличение кинетической энергии электрона:

откуда

где γ— удельный заряд электрона. Разность потенциалов отрицательна. Так как электрон имеет отрицательный заряд, то скорость электрона увеличивается при его движении в сторону возрастания потенциала.

22 В плоский конденсатор влетает электрон со скоростью ν = 20 000 000 м/с, направленной параллельно пластинам конденсатора. На какое расстояние h от своего первоначального направления сместится электрон за время пролета конденсатора? Расстояние между пластинами d=2 см, длина конденсатора l=5 см, разность потенциалов между пластинами v=200 В.

Решение:
За время пролета t = l/v электрон смещается в направлении действия силы на расстояние

где γ — удельный заряд электрона.

23 Положительно заряженная пылинка массы г находится в равновесии внутри плоского конденсатора, пластины которого расположены горизонтально. Между пластинами создана разность потенциалов V₁=6000 В. Расстояние между пластинами d=5см. На какую величину необходимо изменить разность потенциалов, чтобы пылинка осталась в равновесии, если ее заряд уменьшился на q_o=1000 e?

Решение:
На пылинку действуют сила тяжести mg и сила со стороны электрического поля, где —начальный заряд пылинки и E₁ = V₁/d—напряженность электрического поля в конденсаторе.
Чтобы пылинка могла находиться в равновесии, верхняя пластина конденсатора должна быть заряжена отрицательно. При равновесии
mg = F, или ; отсюда .
Так как уменьшение заряда пылинки на q_o=1000e равносильно увеличению положительного заряда на q_o, то новый заряд пылинки q₂ = q₁+q_o. При равновесии , где V2—новая разность потенциалов между пластинами. Учитывая выражения для q2, q1 и q0, найдем

Таким образом, разность потенциалов нужно изменить на V₂— V₁ = — 980 В (знак минус показывает, что ее нужно уменьшить, так как заряд пылинки увеличился).

24 Решить предыдущую задачу, считая пылинку заряженной отрицательно.

Решение:
Верхняя пластина конденсатора должна быть заряжена положительно. Новый заряд пылинки q₂ = q_1-q_o, где q_o=1000e.
Поэтому (см. задачу 23)

Напряжение между пластинами нужно увеличить на V₂— V₁ = 1460 В.

25 В электрическое поле плоского конденсатора, пластины которого расположены горизонтально, помещена капелька масла, имеющая заряд q=1 е. Напряженность электрического поля подобрана так, что капелька покоится. Разность потенциалов между пластинами конденсатора V =500 В, расстояние между пластинами d=0,5 см. Плотность масла . Найти радиус капельки масла.

Решение:
При равновесии
откуда

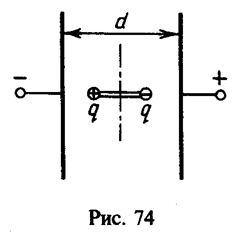
26 Внутри плоского конденсатора, пластины которого расположены вертикально, помещена диэлектрическая палочка длины l=1 см с металлическими шариками на концах, несущими заряды +q и — q(|q|=1 нКл). Палочка может вращаться без трения вокруг вертикальной оси, проходящей через ее середину. Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=10см. Какую работу необходимо совершить, чтобы повернуть палочку вокруг оси на 180° по отношению к тому положению, которое она занимает на рис. 74?

Решение:
Напряженность электрического поля в конденсаторе E=V/d.
Разность потенциалов между точками, где расположены заряды,

где —потенциал в точке расположения заряда + q, а —потенциал в точке расположения заряда — q; при этом . При повороте палочки электрические силы совершают работу по переносу заряда — q из точки а в точку b и заряда + q из точки b в точку а, равную

Знак минус означает, что работу должны совершить внешние силы.

27 Внутри плоского конденсатора помещен диэлектрический стержень длины l=3 см, на концах которого имеются два точечных заряда + q и —q (|q|=8нКл). Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=8 см. Стержень ориентирован параллельно пластинам. Найти момент сил, действующий на стержень с зарядами.

Решение:


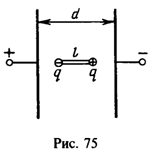
28 На концах диэлектрической палочки длины l=0,5 см прикреплены два маленьких шарика, несущих заряды — q и +q (|q|=10 нКл). Палочка находится между пластинами конденсатора, расстояние между которыми d=10cм (рис.75). При какой минимальной разности потенциалов между пластинами конденсатора V палочка разорвется, если она выдерживает максимальную силу растяжения F=0,01 Н? Силой тяжести пренебречь.

Решение:


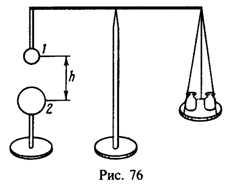
29 Металлический шарик 1 радиуса R₁=1 см прикреплен с помощью диэлектрической палочки к коромыслу весов, после чего весы уравновешены гирями (рис. 76). Под шариком 1 помещают заряженный шарик 2 радиуса R₂=2 см. Расстояние между шариками h = 20 см. Шарики 1 и 2 замыкают между собой проволочкой, а потом проволочку убирают. После этого оказывается, что для восстановления равновесия надо снять с чашки весов гирю массы m = 4мг. До какого потенциала j был заряжен шарик 2 до замыкания его проволочкой с шариком 1?

Решение:
Если до замыкания шарик 2 имел заряд 0, то сумма зарядов шариков 1 и 2 после замыкания q₁+q₂ = q. Потенциалы же их после замыкания одинаковы: . Следовательно, После замыкания шарик 2 действует на шарик 1 с силой
откуда
Начальный потенциал шарика 2