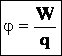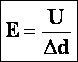Условие задачи:
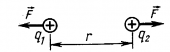
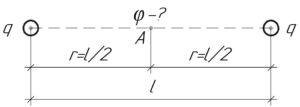
Найти потенциал электрического поля в точке, лежащей посредине между двумя зарядами по 50 нКл, расположенными на расстоянии 1 м в вакууме.
Задача №6.3.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(q=50) нКл, (r=frac{l}{2}), (l=1) м, (varphi-?)
Решение задачи:
[{varphi _0} = frac{{kq}}{r}]
Здесь (k) – коэффициент пропорциональности, равный 9·109 Н·м2/Кл2.
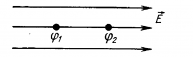
Учитывая, что точка A находится посредине между двумя зарядами ((r=frac{l}{2})), то:
[{varphi _0} = frac{{2kq}}{l}]
Искомый потенциал (varphi) равен сумме потенциалов электрических полей в точке A, создаваемых каждым зарядом, поскольку потенциал – величина скалярная. Учитывая вышесказанное, имеем:
[varphi = {varphi _0} + {varphi _0}]
[varphi = 2{varphi _0}]
В итоге решение задачи в общем виде выглядит так:
[varphi = frac{{4kq}}{l}]
Произведём вычисления:
[varphi = frac{{4 cdot 9 cdot {{10}^9} cdot 50 cdot {{10}^{ – 9}}}}{1} = 1800;В = 1,8;кВ]
Ответ: 1,8 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.8 На расстоянии 1 м от центра заряженного металлического шара радиусом 3 м
6.3.10 Сколько электронов следует передать металлическому шарику радиусом 7,2 см
6.3.11 Определить разность потенциалов (по модулю) между точками, отстоящими
|
Потенциал. Разность потенциалов. Напряжение. |
|
|
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: — энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. |
|
|
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора. |
|
|
— следствие принципа суперпозиции полей (потенциалы складываютсяалгебраически). |
|
|
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах: |
|
|
Разность потенциалов |
|
|
|
|
|
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат! |
|
|
Единица разности потенциалов
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж. |
|
|
Связь между напряженностью и напряжением. |
|
|
Из доказанного выше: напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d). |
|
|
Из этого соотношения видно:
|
|
|
Эквипотенциальные поверхности. ЭПП — поверхности равного потенциала. Свойства ЭПП: — работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; — вектор напряженности перпендикулярен к ЭПП в каждой ее точке. |
|
|
|
|
|
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр. |
|
|
Потенциальная энергия взаимодействия зарядов. |
|
|
|
|
|
Потенциал поля точечного заряда |
|
|
|
|
|
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда. |
|
|
Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными. |
Физика, 10 класс
Урок 27. Напряжённость и потенциал электростатического поля. Разность потенциалов
Перечень вопросов, рассматриваемых на уроке:
1) Теория дальнодействия;
2) Теория близкодействия;
3) Электрическое поле;
4) Скорость электрического поля;
5) Напряжённость электрического поля;
6) Однородное и неоднородное электрическое поле;
7) Принцип суперпозиции полей;

9) Электростатическая защита
10) Работа электрического поля;
11) Потенциал и разность потенциалов.
Глоссарий по теме:
Напряжённость — отношение силы, действующей на помещаемый в данную точку поля точечный заряд, к этому заряду.
Потенциал точки электростатического поля -отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду.
Напряжение – разность потенциалов.
Потенциальное поле – поле, работа которого по перемещению заряда по замкнутой траектории всегда равна нулю.
Напряжённость направлена в сторону убывания потенциала.
Эквипотенциальные поверхности – поверхности равного потенциала.
Свободные заряды — заряженные частицы, способные свободно перемещаться в проводнике под влиянием электрического поля.
Электростатическая индукция – явление разделения зарядов и их распределение по поверхности проводника во внешнем электрическом поле.
Основная и дополнительная литература
Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 290 – 320.
Рымкевич А.П. Сборник задач по физике. 9 – 11 класс. М. Дрофа, 1999 – С. 93 — 102
Теоретический материал для самостоятельного изучения
Согласно идее Фарадея электрические заряды не действуют друг на друга непосредственно. Каждый из них создаёт в окружающем пространстве электрическое поле.
Электрическое поле — это особый вид материи, посредством которой происходит взаимодействие зарядов. Скорость распространения электрического поля в вакууме равна 300000 км/с.
Напряжённость Е — силовая характеристика электрического поля.
Электрическое поле, напряженность которого одинакова во всех точках, называется однородным. Поле между параллельными пластинами однородно
Главное свойство электрического поля – это действие его на электрические заряды с некоторой силой.
Напряжённость-это отношение силы, действующей на помещаемый в данную точку поля точечный заряд, к этому заряду.
Если в данной точке пространства различные заряженные частицы создают поля, напряжённости которых Е1, Е2, то результирующая напряжённость поля в этой точке равна геометрической сумме напряжённостей этих полей. В этом состоит принцип суперпозиции полей.

Заряд, помещенный в электрическое поле обладает потенциальной энергией.
Потенциалом φ точки электростатического поля называют отношение потенциальной энергии Wn заряда, помещённого в данную точку, к этому заряду q.
Напряжение – это работа, совершаемая полем при перемещении заряда 1Кл.


Примеры и разбор решения заданий
1. К каждой позиции первого столбца подберите соответствующую позицию второго
|
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
ФОРМУЛЫ |
|
Напряженность |
|
|
Потенциал |
|
|
Потенциальная энергия заряда в однородном электростатическом поле |
|
|
Разность потенциалов |
qΕd |
Решение: вспомнив формулы величин, можем установить:
|
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
ФОРМУЛЫ |
|
Напряженность |
|
|
Потенциал |
|
|
Потенциальная энергия заряда в однородном электростатическом поле |
qΕd |
|
Разность потенциалов |
|
2. В однородном электрическом поле напряжённостью 1 В/м переместили заряд -25 нКл в направлении силовой линии на 2 см. Найти работу поля, изменение потенциальной энергии заряда и напряжение между начальной и конечной точками перемещения.
Решение.
Работа электрического поля при перемещении заряда вдоль силовой линии:
ΔA = — qΕΔd,
при этом изменение потенциальной энергии равно:

Напряжение между начальной и конечной точками перемещения равно:

Вычисления:
ΔA = -25 · 10-9 Kл · 103 B/м · 0,02 м = -0,5 мкДж;


Ответ: 
Если
в одну и ту же точку данного
электростатического поля помещать
пробные заряды, например, кратные q0:
qо1
= qo,
qo2
= 2qo,
… , qon=
nqo,
то
они будут характеризоваться различным
значением потенциальной энергии:
Wp1=
Wp,
Wp2
= 2Wp,
… , Wpn=
nWp.
Отношение
потенциальной энергии к соответствующей
величине пробного заряда всегда будет
величиной постоянной, т. е.
,
(24)
Величину
называют потенциалом
электростатического поля в данной
точке.
Таким
образом, для описания электростатического
поля, кроме силовой характеристики
напряженности
вектора
,
используют скалярную энергетическую
характеристику этого поля
потенциал
.
Используя
формулу (18), найдем потенциал
электростатического поля точечного
заряда q
на расстоянии r
от него в СИ:
.
(25)
Если
среда, окружающая заряд безграничный
диэлектрик с проницаемостью ,
то потенциал электростатического поля
точечного заряда q
на расстоянии r
.
(26)
Если электростатическое
поле создано системой точечных зарядов:
q1,
q2,
… , qn,
то
на основании (18):
потенциал
результирующего поля равен алгебраической
сумме потенциалов, создаваемых каждым
из зарядов в отдельности,
т. е.
.
(27)
Из
(25) следует, что заряд q0,
находящийся
в произвольной точке электростатического
поля с потенциалом ,
характеризуется потенциальной энергией
Wp
= q0.
(28)
Физический
смысл имеет не сам потенциал поля, а
разность потенциалов, поэтому работа
сил этого поля над зарядом qo
записывается в виде
А=
Wp1
Wp2
= q0(1
2),
(29)
где
1
и 2
потенциалы
электрического поля
начальной и конечной точек перемещения
пробного заряда.
Если
заряд q0
из точки с потенциалом
удаляется на бесконечность, где потенциал
равен нулю (
= 0) или
перемещается из бесконечности в данную
точку поля, то
А
= q0.
(30)
В
СИ за единицу потенциала принят вольт
(В).
7. Связь между е и
Электрическое
поле полностью описывается векторной
функцией
.
В этом случае можно найти силу, действующую
на пробный заряд в любой точке поля, и
вычислить работу поля при любом
перемещении пробного заряда.
Но
электрическое поле также характеризуется
и потенциалом
.
Следовательно,
между ними существует связь. Действительно,
согласно (21) и (29), для единичного,
положительного заряда (qo=
+1 Кл) имеем
.
(31)
Формула
(31) остается справедливой не только для
конечных, но и для элементарных перемещений
,
т. е.
или
.
(32)
Следовательно,
проекция вектора
на направление
равна со знаком минус первой производной
потенциала по данному направлению.
Если
перемещение
параллельно оси Х, то
=
dx,
где
единичный вектор оси Х; dx
приращение координаты х. Исходя из
этого, получим
()
=dx
= Exdx,
где
Ех
проекция вектора
на ось Х.
Значит,
с учетом (1.55) последнее выражение запишем
в виде
,
(33)
где
символ частной производной
свидетельствует о том, что функцию
=
(х,
у, z)
необходимо дифференцировать только по
х, считая у, и z
постоянными.
Аналогично
можно найти выражения для проекций Еу
и Еz,
т. е.
,
,
.
Зная
проекции вектора
на оси координат можно найти и сам
вектор,
.
(34)
В
формуле (34) выражение в скобках является
градиентом потенциала
(grad
или
).
Таким образом,
=
grad
=
.
(35)
Знак
«»
означает,
что вектор
направлен в сторону убывания потенциала;
векторный оператор «набла».
Потенциал электростатического поля как его энергетическая характеристика. Из выражений (21.1) и (21.2) следует, что потенциальная энергия пробного заряда q0 в данной точке поля пропорциональна величине этого заряда. Следовательно, отношение не зависит от заряда и является энергетической характеристикой электростатического поля, получившей название потенциал.
Потенциал электростатического поля в данной точке пространства — физическая скалярная величина, равная отношению потенциальной энергии пробного заряда, помещённого в данную точку поля, к значению этого заряда:
(21.4)
За единицу потенциала в СИ принят вольт (В). Единица названа в честь итальянского учёного Алессандро Вольта (1745–1827), внёсшего большой вклад в изучение электрических явлений. 1 В — потенциал такой точки электростатического поля, в которой заряд 1 Кл обладал бы потенциальной энергией 1 Дж.
Потенциал φ электростатического поля точечного заряда Q на расстоянии r от него в вакууме или в воздухе определяют соотношением
(21.5)
Знак заряда-источника поля определяет знак потенциала этого поля.
Поскольку потенциальная энергия заряда в электростатическом поле зависит от выбора нулевой точки, то эта зависимость сохраняется и для потенциала. Если принять, что на бесконечно большом расстоянии от источника поле отсутствует, т. е. потенциальная энергия системы «заряд ‒ электростатическое поле» на бесконечности равна нулю, то потенциал поля в данной точке можно определить следующим образом:
Если электрическое поле создано в однородной среде с диэлектрической проницаемостью ε, то потенциал поля
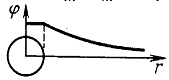
Следует отметить, что потенциал поля, создаваемого положительным зарядом, уменьшается по мере удаления от заряда, а потенциал поля, создаваемого отрицательным зарядом, увеличивается.
Из формулы (21.5) следует, что во всех точках поля, находящихся на расстоянии r от точечного заряда Q, потенциал φ одинаковый. Эти точки расположены на поверхности сферы радиусом R, центр которой находится в той же точке, что и заряд Q.
Потенциал поля, создаваемого равномерно заряженной сферой радиусом R, заряд которой Q, в вакууме в точках вне сферы на расстоянии r > R от её центра, определяют по формуле . В точках, находящихся на поверхности и внутри сферы по формуле
.
От теории к практике
Электростатическое поле создано точечным неподвижным зарядом Q. Потенциал поля в точке, расположенной от заряда Q на расстоянии r = 27 см, φ = 80 В. В эту точку помещают пробный заряд q0. Определите: а) значение заряда, создающего поле; б) значение пробного заряда, если его потенциальная энергия в данной точке поля Wп = –0,8 мкДж.
Потенциал является скалярной величиной. Поэтому, если в данной точке пространства электростатическое поле создано системой точечных зарядов, то потенциал результирующего поля в этой точке равен алгебраической сумме потенциалов полей в этой же точке пространства, создаваемых каждым из точечных зарядов системы в отдельности:
φ = φ1 + φ2 + φ3 + … + φn,
т. е. для потенциала выполняется принцип суперпозиции.
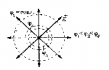
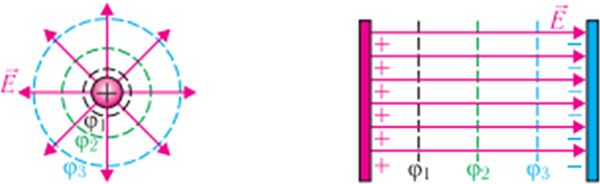
Геометрическое место точек в электростатическом поле, потенциалы которых одинаковы, называют эквипотенциальной поверхностью.
Используя эквипотенциальные поверхности, можно представлять графически электростатические поля. Через каждую точку поля проходят только одна линия напряжённости и одна эквипотенциальная поверхность. В каждой точке электростатического поля линия напряжённости и эквипотенциальная поверхность взаимно перпендикулярны (рис. 116.1). Представление электростатического поля с помощью эквипотенциальных поверхностей, как и термин «потенциал», ввёл немецкий учёный К. Ф. Гаусс в 1840 г.
1. Как определить работу силы однородного электростатического поля по перемещению электрического заряда?
2. Как вы понимаете утверждение «электростатическое поле потенциально»? Как связана работа силы электростатического поля по перемещению электрического заряда с изменением потенциальной энергии заряда в этом поле?
3. Какие две физические величины характеризуют электростатическое поле в любой его точке?
4. Что называют потенциалом электростатического поля?
5. Чему равен потенциал электростатического поля точечного заряда Q на расстоянии r от него?
6. Как определить потенциал электростатического поля, созданного несколькими точечными зарядами?
7. Докажите, что работа силы электростатического поля по перемещению заряда по замкнутой траектории равна нулю.
8. В чём проявляется сходство электростатического и гравитационного полей?
9. Положительно заряженная частица перемещается под действием только сил электростатического поля на некоторое расстояние. В какой точке траектории движения частицы — начальной или конечной — потенциал поля выше, если модуль её скорости: а) возрастает; б) убывает?
10. Отрицательно заряженная частица перемещается из состояния покоя под действием только сил электростатического поля на некоторое расстояние. В какой точке траектории движения частицы — начальной или конечной — потенциал поля выше?
11. Чему равен потенциал электростатического поля равномерно заряженной сферы радиусом R на расстоянии r от её центра, если: а) r ≤ R; б) r > R, а заряд сферы Q?