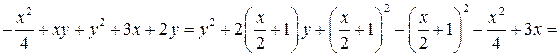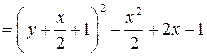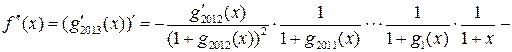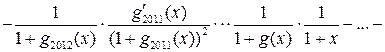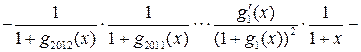Найдите последнюю цифру в десятичной записи числа 1!+2!+…+2017! ( Факториалом натурального числа n называется произведение всех последовательных натуральных чисел от 1 до n , то есть n!=1*2*3*…*(n-2)*(n-1)*n. РАСПИШИТЕ ПОДРОБНО, ПОЖАЛУЙСТА.
Светило науки — 1821 ответ — 10162 помощи
Все слагаемые начиная с 5! будут делиться на 2 и на 5, а значит будут делиться и на 10, т.е. их последняя цифра будет равна 0. Ну и 1!+2!+3!+4!=1+2+6+24=33. Значит итоговое число будет равно 33 плюс очень много чисел оканчивающихся на 0, т.е. посленяя цифра будет 3.
Тема 18.
Задачи на теорию чисел
18
.
09
Последняя цифра числа
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
задачи на теорию чисел
Решаем задачи
Делится ли число на
?
Найдите последнюю цифру числа:
а)
б)
в)
Показать ответ и решение
а) Заметим, что последняя цифра произведения двух натуральных чисел такая же, как последняя
цифра произведения последних цифр этих двух чисел.
То есть предположим, что нам нужно найти последнюю цифру произведения чисел и
.
Для этого нам нужно перемножить последние цифры этих чисел, то есть , и так
последняя цифра у – это
, то последняя цифра произведения чисел
и
тоже
.
Пользуясь этим правилом, составим последовательность последних цифр степеней тройки:
Заметим, что в этой последовательности блоки по четыре цифры повторяются, значит,
последняя цифра числа зависит от того, какой остаток будет давать число
при делении на
(так как блоки по цифры).
Так как остаток при делении на
равен
, то
заканчивается на такую же цифру, как и
. Таким образом, последняя цифра числа
– это
.
б) Аналогично решая данный пункт задачи, найдем, что последняя цифра числа – это
.
в) Аналогично решая данный пункт задачи, найдем, что последняя цифра числа – это
.
Показать ответ и решение
Докажем методом от противного: пусть такие числа ,
существуют. Пусть при этом
,
тогда какой может быть последняя цифра числа ?
Ответ на последний вопрос зависит от последней цифры числа . Рассмотрим все возможные
варианты:
1) последняя цифра числа – это цифра
, тогда последняя цифра числа
– это цифра
, но
не может содержать в своей записи цифру .
2) последняя цифра числа – это цифра
, тогда последняя цифра числа
– это цифра
, но
не может содержать в своей записи цифру .
3) последняя цифра числа – это цифра
, тогда последняя цифра числа
– это цифра
, но
не может содержать в своей записи цифру .
4) последняя цифра числа – это цифра
, тогда последняя цифра числа
– это цифра
, но
не может содержать в своей записи цифру .
Таким образом, подходящих и
не существует.
Найдите последнюю цифру числа, равного , если
– по определению.
Показать ответ и решение
Последняя цифра суммы равна последней цифре суммы последних цифр исходных слагаемых.
Так как при последняя цифра числа
равна
, то все числа вида
при
не дадут
вклада в последнюю цифру исходной суммы.
Таким образом, последняя цифра исходной суммы совпадает с последней цифрой суммы
которая равна последней цифре суммы последних цифр её слагаемых, то есть последней цифре
числа
которой является цифра .
Ответ:
Академик Котовский нашел самое большое простое число: . Не перепутал ли чего
академик?
Показать ответ и решение
Так как последняя цифра числа равна
, то
– чётное, следовательно,
– чётное, тогда
делится на , что равносильно тому, что число, образованное двумя последними цифрами числа
,
делится на .
Не более чем двузначные числа, у которых последняя цифра равна , которые и сами делятся на
:
Таким образом, предпоследняя цифра числа обязательно чётна.
Докажите, что все числа вида при всевозможных натуральных
больших четырёх, оканчиваются на одну и ту же
цифру.
Показать ответ и решение
При имеем:
— делится на 10, следовательно, последняя цифра такого числа равна 0.
Ответ:
Задача на доказательство
Вася записал число, равное , в десятичной системе исчисления. Затем он стёр
последних
цифр записанного числа. Какой цифрой оканчивается число, полученное в итоге Васей?
Показать ответ и решение
Понятно, что несколько последних цифр этого числа будут равны (в произведении
есть множители ,
,
).
Пусть некоторое число делится на , тогда последние
цифр в его десятичной записи равны
.
Число делится на тогда и только тогда, когда оно делится на
и на
.
Чисел, которые делятся на и не превосходят
, ровно
(здесь
– целая часть
).
Чисел, которые делятся на и не превосходят
, ровно
.
Чисел, которые делятся на и не превосходят
, ровно
.
Чисел, которые делятся на и не превосходят
, ровно
.
При чисел, которые делятся на
и не превосходят
нет.
Тогда делится на
, следовательно, последние
цифры этого числа равны
. Таким
образом, число, которое в итоге получил Вася, также оканчивается на .
Ответ:
Найдите все натуральные такие, что к десятичной записи числа
справа можно дописать
две цифры так, что полученное число будет квадратом некоторого натурального числа.
Показать ответ и решение
Дописывание к десятичной записи числа цифр и
эквивалентно умножению исходного числа на
и прибавлению к нему
:
По условию полученное число должно быть равно для некоторого натурального
,
тогда:
Обозначим ,
– натуральное.
Тогда для того, чтобы подходило по условию, необходимо и достаточно, чтобы для некоторого
натурального и некоторого натурального
было выполнено
Первый множитель – натуральное число, так как оно целое и его произведение с
натуральным числом даёт натуральное число.
Так как произведение не превосходит , то
.
Так как (
) и
, то
, тогда
Таким образом, имеет смысл проверить только .
Для достаточно положить
,
.
Легко проверить, что при :
– не
может быть выполнено при ,
.
Для и
– аналогично.
Таким образом, условие задачи выполняется только для .
Для целых чисел все просто, как уже верно заметил Stalker_RED достаточно взять остаток от деления на 10n % 10
Но вот с дробными числами все намного интереснее. Потенциально, можно получить целое представление последовательно умножая число на 10 (сдвигая тем самым десятичную точку вправо), а после воспользоваться предыдущим приемом. Но проблема тут в том, что потенциально такая последовательность может оказаться бесконечной и такой алгоритм зациклится.
Если обратится к стандарту IEEE 754, то можно узнать, что в 64 битах можно точно представить не более 16 десятичных разрядов, а это уже можно использовать как ограничитель, так как при превышении 16 сдвигов десятичной точки значение все равно уже не будет точным
const lastDigit = n => {
// в n совсем не то
if (isNaN(n) || !isFinite(n)) return NaN;
// в n целое
if (n % 1 === 0) return n % 10;
// для дробных проще со строкой работать
const s = String(Math.abs(n));
// неточные значения
if (s.length > 16 || s.includes('e')) return NaN;
return +s.slice(-1);
}РЕШЕНИЯ ЗАДАЧ ДЛЯ СТУДЕНТОВ 1 КУРСА
1.
Последняя цифра в
десятичной записи числа ,
,
равна 4. Найти предпоследнюю цифру.
Решение. Число оканчивается
на 5, следовательно, две его последние цифры – 25. Соответственно, у числа две
последние цифры 24.
2.
На окружности радиуса
1 отмечены 2013 точек. Доказать, что на окружности существует точка, сумма
расстояний от которой до отмеченных точек больше 2013.
Решение. Пусть –
отмеченные точки. Возьмем на окружности две диаметрально противоположные точки и
.
Тогда
,
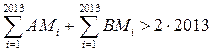
Следовательно, либо 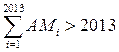
либо 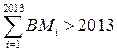
3.
Найти определитель
матрицы ,
если ,
.
Решение. У матрицы пропорциональные
строки, поэтому ее определитель равен нулю.
4.
Найти матрицу,
обратную к квадратной матрице го
порядка с
элементами при
и
при
.
Решение. Запишем матрицу в виде ,
где –
матрица, все элементы которой равны 1. Будем искать обратную матрицу в виде .
Из условия получаем
.
Ясно, что .
Поэтому ,
и
.
5.
Доказать, что для
любого
.
Решение. Из неравенства ,
верного для всех ,
,
при получаем
.
Так как ,
то и,
окончательно, .
6.
Решить уравнение .
Здесь –
целая часть числа –
наибольшее целое число .
Решение. При уравнение
решений не имеет, так как и
.
При
,
поэтому получаем уравнение и
решение .
При
и
получаем уравнение и
решение .
При получаем
уравнение и
решение .
Ясно, что решением
не является. При уравнение
решений не имеет, так как и
.
Итак, решения уравнения: .
7.
Сколько действительных
корней имеет уравнение ?
Решение. Рассмотрим функцию .
Так как ,
то при
и
,
при
и
при ,
при
.
Поэтому на промежутке наименьшее
значение равно
и
уравнение не имеет корней на этом промежутке. На промежутке
возрастает
и меняет знак. Поэтому уравнение имеет единственный корень.
8.
Найти .
Решение. Так как
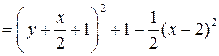
то
, а
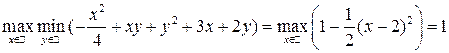
Ответ: 1.
9.
Найти 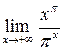
Решение. Используя правило
Лопиталя и неравенство ,
получаем 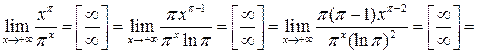
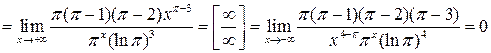
Ответ: 0.
10.
Для функции найти
.
Решение. Обозначим,
,
.
Тогда .
При любом имеем
,
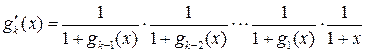
.
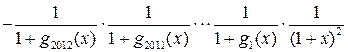
В этой сумме 2013 слагаемых. При каждое
слагаемое равно -1. Следовательно, .
В общем случае здесь обычно применяется теорема Эйлера. Скажем, есть какая-то «высокая» степень, и надо найти последние две десятичные цифры. Это значит, что мы решаем задачу по модулю $%100$%. Тогда показатель степени нас интересует по модулю $%varphi(100)=40$%. Задача нахождения остатка по модулю $%40$% сводится к случаю остатков в показателе по модулю $%varphi(40)=16$%, и так далее. Рано или поздно мы получим задачу по модулю $%1$%, где всё известно, и останется применить «обратный ход».
Скажем, то число, которое здесь указано, оканчивается, если я не ошибаюсь, на $%43$%.