Как найти полярное время - Avtoru.top - решение различных проблем

‍Полярный день

Приложения: мир вокруг нас

Математика: тригонометрические функции, график функции, задачи с параметром

Дни весеннего и осеннего равноденствия геометрически можно определить как моменты, когда ось вращения оказывается в плоскости терминатора. Из этого вытекает житейски привычное определение дней равноденствия: в любой точке Земли, на любой широте продолжительность дня равна продолжительности ночи.

Дни летнего и зимнего солнцестояния — моменты, когда ось Земли максимально отклонена от плоскости терминатора; продолжительность дней и ночей — экстремальна. Шапочки полярных дней и ночей становятся максимальными, их границы, широтные окружности, называются, соответственно, Северным и Южным полярным кругом. Из геометрического определения дней солнцестояния следует, что широта Северного (Южного) полярного круга равна $90°-varepsilon=66° 34’$ ($-66° 34’$). За полярными кругами наблюдаются полярные дни и полярные ночи, а в полосе между Северным и Южным полярными кругами их не бывает.

Чтобы наглядно представить годовую динамику продолжительности светового дня и размеров шапочки полярного дня/ночи, выберем начальную точку отсчёта — день весеннего равноденствия и географическую область — Северное полушарие.

В течение трёх месяцев от весеннего равноденствия до летнего солнцестояния появляется и растёт шапочка полярного дня вокруг Северного полюса, в этой области день становится круглосуточным. Но и вне увеличивающейся шапочки дни становятся всё длиннее. Ось вращения Земли всё больше «смотрит» на Солнце, а землянам кажется, что оно с каждым днём поднимается всё выше над горизонтом. Летнее солнцестояние — время максимумов. Затем долгота дня и размер шапочки начинают уменьшаться, в день осеннего равноденствия день и ночь уравновешиваются, шапочка исчезает. В интервале между осенним и весенним равноденствиями история повторяется, только день и ночь меняются местами.

Динамика продолжительности дня/ночи и размеров полярных шапочек напоминает поведение синуса, но чтобы ассоциации превратить в инструменты, надо правильно выбрать аргументы. Орбита Земли — эллипс, но вытянутый совсем немного, так что в упрощённых расчётах можно заменить его окружностью. Положение точки на окружности задаётся углом в пределах от 0 до $2π$, в задаче о длительности дня естественный параметр — номер этого дня в календаре, от 1 до 365. Угловая метка дня с номером $n$ равна $2πcdotfrac{n}{365}$, а с учётом сдвига точки отсчёта на день весеннего равноденствия (20 марта — 81‐й день в году) приходим к «правильному» аргументу: $2πcdotfrac{n-81}{365}$.

В главной задаче определения длительности дня геометрически дело сводится к нахождению длин двух кусков широтной окружности, на которые она разбивается пересечением с терминатором. Технически решение задачи естественным образом приведёт к использованию тригонометрических функций. Вот итоговая формула для вычисления продолжительности светового дня в точке Земли на широте $s$ ($-90°<s<90°$) в день $n$ ($1le n le 365$):

$$ frac{24}{π}arccos(-{tg s} cdot tgarcsin(sinvarepsilon cdot sin N)), hbox{ где } N=frac{2π}{365}cdot(n-81). $$

В формуле аргументы тригонометрических функций представлены и в градусной мере ($s$ и $varepsilon$), и в радианной ($N$, значения функций arccos и arcsin), результат измеряется в часах.

Чтобы увидеть эту формулу в действии, можно построить график зависимости продолжительности светового дня от номера дня в году, например, для Москвы ($55° 45’$ с. ш.). Каждый вертикальный отрезок (сутки) делится графиком на день (часть под графиком) и ночь (над графиком). В дни равноденствия эти части совпадают (день и ночь по 12 часов), в дни солнцестояния — максимум и минимум функции.

Источник

Довольно интересный способ помогающий определить время ночью. Использование созвездия большой медведицы.

Но данный способ подойдёт лишь для северного полушария, к тому же летом созвездие находится ближе к горизонту что может затруднить определение времени. Не возможно воспользоваться данным способом и в условиях плохой видимости неба, при наличии облаков.

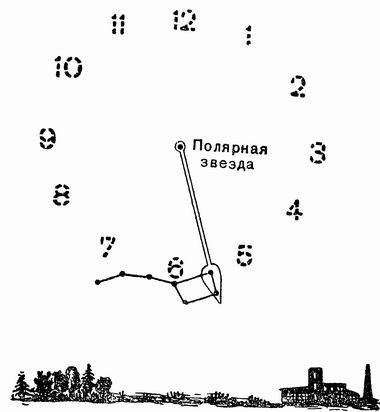
1. Представьте, что часть неба, это часы! Где две первых звезды ковша «большой медведицы» играют роль кончика стрелки, которая также мысленно представляется и крепится в центре воображаемых часов за полярную звезду. Представьте двенадцати часовой циферблат и просто взгляните куда указывает наша стрелка. Всё описанное выше хорошо иллюстрирует приведённый ниже рисунок.

2. Однако полученное время весьма приблизительно, и необходимо скорректировать его добавив по часу к каждому месяцу после даты 7 марта. (в марте + 1 час, в мае + 2 часа, в апреле + 3 и т.д.).

3. Но и это время не совсем точное, следует прибавить или наоборот вычесть ещё и минуты в зависимости от даты наблюдения. То-есть, если до 7 числа месяца, вычитаем по 2 минуты за каждый день, если после седьмого числа — прибавляем.

Пример: если сегодня второе февраля (1 месяц и 5 дней до 7 марта) а время на наших воображаемых часах указывает на 2:30 значит при вычитании мы получим время равное 1.20.

Седьмое марта как ориентир используется не зря, ведь именно в этот день звёздные часы показывают ровно 12:00 в полночь.

Если вы не умеете находить полярную звезду, сделать это довольно просто. Найдите на небе ковш это 7 наиболее ярких звёзд созвездия «большая медведица» визуально напоминающие ковш. Теперь взглянем на начало ковша и возьмём две первых звезды. Между ними мысленно проведём линию, отмерив примерно 5 расстояний. Звезда в которую упрётся взгляд и будет полярной звездой. По которой можно легко сориентироваться и по сторонам света, всё это мы уже описали в другой нашей статье.

4
2
голоса

Рейтинг статьи

Post Views: 10 001

Источник

Как определить время с точностью до нескольких минут, если у вас нет часов, но есть звездное небо над головой

Условный счет звездных часов

Каждая звезда Большой Медведицы в течение суток описывает круг около Полярной звезды (вращается все созвездие целиком).

Прямую линию от Полярной звезды к звездам 1 и 2 Большой Медведицы будем для краткости называть стрелкой Медведицы.

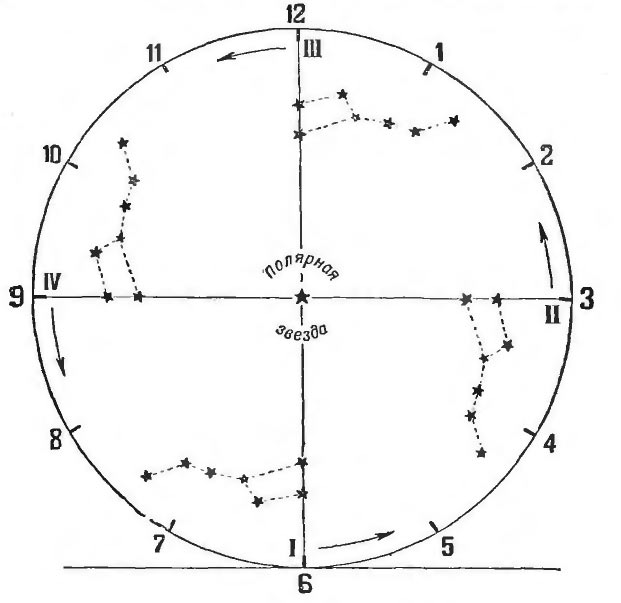
Когда звезды 1 и 2 стоят прямо под Полярой звездой, то стрелка направлена отвесно вниз. Условимся говорить, что она показывает 6 часов, по условному счету. Это будет положение I на рисунке.

Продолжая наблюдение, мы скоро заметим, что в этом положении Большая Медведица движется вправо, т. е. к востоку, и медленно подымается, но кругу, центром которого служит Полярная звезда. Через четверть суток, т. е. через 6 настоящих часов, стрелка Медведицы пройдет четверть оборота окружности, будет теперь располагаться не вертикально, а горизонтально, и мы получим положение II; теперь стрелка Медведицы показывает 3 часа по условному счету и т. д.

«Циферблат звездных часов» и «звездное время»

Так как движение Большой Медведицы вокруг Полярной звезды совершается равномерно, то можно сказать, что Большая Медведица вместе с Полярной звездой— это условные звездные часы. Стрелкой у этих небесных часов служит воображаемая линия, проходящая от Полярной звезды к звездам 1 и 2 Большой Медведицы, но циферблата совсем нет. Но ведь циферблат и не особенно нужен. Когда мы смотрим на часы, мы очень часто определяем время просто по направлению стрелок и вовсе не стараемся рассмотреть цифру, на которую стрелка указывает.

Стрелка небесных часов поворачивается в направлении, обратном движению стрелки обычных часов. После положения II она будет проходить воображаемые цифры, соответствующие условным 2 ч., 1 ч., 12 ч., 11 ч. и т. д. Будем крепко помнить, что это не настоящие часы, а условные показания нашей воображаемой стрелки.

Ниже описано, какие задачи можно решать с помощью этих воображаемых небесных часов.

Как по Большой Медведице узнать, сколько времени прошло?

3адача 1. Вообразим себе, что боец, не имеющий часов, вышел в ночную разведку, когда Большая Медведица еще не дошла до самого низкого положения. На глаз он определил, что стрелка Медведицы стоит показывает на 6,5 условных часов. После выполнения задания он взглянул на Большую Медведицу и увидел, что теперь ее стрелка показывала 4,0 условных часа. Сколько времени он провел в разведке?

Для ответа на вопрос надо из 6,5 вычесть 4,0. В итоге мы получим 2,5 (условных часа).

Чтобы перевести условные часы в истинные, нужно умножить результат на 2. Итак, 2,5 х 2 = 5 часов (истинных).

Следовательно, разведка продолжалась приблизительно 5 часов.

Задача 2. Сколько времени прошло, если в начале стрелка Медведицы показывала 2,0 условных часа, а в конце 10,5 условных часов?

Чтобы из 2 часов можно было вычесть10,5, нужно сначала прибавить к 2 часам 12 часов (не забывайте, «условные часы» идут в обратную сторону по отношению к истинным):

2 условных часа +12 условных часов=14 условных часов. Вычитаем:

14 условных часов – 10,5 условных часов = З,5 условных часа. Для перевода условных часов в истинные, умножаем 3,5 условных часа на 2 и получаем 7 истинных часов.

Отсюда получаем такое правило:

Чтобы по Большой Медведице определить, сколько времени прошло, надо:

1) заметить, сколько показывала стрелка Медведицы на воображаемых небесных часах вначале и в конце.

2) из первого числа вычесть второе (если первое число меньше второго, то прибавить к первому 12 и после этого вычесть второе).

3) полученное число умножить на два.

Как по Большой Медведице узнать, что наступила полночь?

Эта задача труднее предыдущей потому, что звезды Большой Медведицы (как и все другие звезды) совершают полное обращение не ровно в 24 часа, а на 4 минуты скорее.

Другими словами, наши звездные часы каждый день уходят вперед против обыкновенных часов на 4 минуты. Поэтому самое низкое положение Большой Медведицы по обыкновенным часам завтра придется на 4 минуты раньше, чем было сегодня, послезавтра — на 8 минут раньше и так далее. Через 30 дней оно наступит раньше, чем сегодня, уже на 120 минут, т. е. на целых 2 часа. Несмотря на всю эту сложность, в названной задаче легко разобраться при помощи следующих сведений.

22 сентября стрелка Медведицы в полночь (т. е. в 0 час. 00 мин. по нашим часам) направлена отвесно вниз и показывает на небесных часах 6 условных часов.

Через месяц после 22 сентября, т. е. 22 октября, это отвесное положение стрелки наступит уже за два истинных часа до полуночи. Поэтому в полночь 22 октября небесная стрелка уже не будет стоять отвесно, а отклонится к востоку (вправо) на такой угол, как будто она направлена к цифре 5 на воображаемых небесных часах. Рассуждая таким же образом дальше, получим следующую табличку.

Стрелка Большой Медведицы в полночь показывает:

22 сентября	6 часов (условных)
22 октября	5 часов (условных)
22 ноября	4 часа (условных)
22 декабря	3 часа (условных)
22 января	2 часа (условных)
22 февраля	1 час (условных)
22 марта	12 часов (условных)
22 апреля	11 часов (условных)
22 мая	10 часов (условных)
22 июня	9 часов (условных)
22 июля	8 часов (условных)
22 августа	7 часов (условных)
22 сентября	6 часов (условных)

Числа эти нетрудно рассчитать и без таблички, если помнить первую строку и знать, что каждый месяц показание условных часов уменьшается на один условный час.

Решим, например, такую задачу:

Задача 3. Как узнать по Большой Медведице, что наступила полночь 7 ноября?

7 ноября приходится посредине между 22 октября и 22 ноября. Поэтому из таблицы мы найдем, что в этот день в полночь стрелка Медведицы должна покапывать 4,5 условных часа.

Значит, полночь наступит в то время, когда Большая Медведица займет положение как раз посредине между положением I (6 условных часов) и II (3 условных часа) на рис. 10.

Как по Большой Медведице узнать, который час?

Узнать который час — это значит определить, сколько времени прошло от полуночи. При помощи вышеприведенной таблицы это сделать легко.

Задача 4. 7 ноября стрелка Медведицы показывала условных часа. Который час на самом деле?

В прошлой задаче мы уже определили из таблицы, что в полночь стрелка Медведицы 7 ноября показывает 4,5 условных часа. Чтобы узнать искомое время, надо из 4,5 условных часов вычесть 2 условных часа в результат умножить на 2: 4,5-2=2,5 условных часа.

Умножаем результат на 2: 2,5 х 2 = 5 истинных часов (утра).

3адача 5. 20 октября стрелка Медведицы показывала 7 условных часов. Который час на самом деле?

Из таблицы для 20 октября получим, что в полночь стрелка Медведицы показывает приблизительно 5 условных часов. Чтобы вычесть из 5 часов 7 часов, сначала к 5 часам прибавим 12 часов:

5+12=17 условных часов; 17 условных часов – 7 условных часов=10 условных часов. Умножаем результат на 2:

10 х 2 = 20 истинных часов (вечера).

Отсюда ещё одно правило:

Чтобы по положению стрелки Большой Медведицы узнать который час, надо:

1) из таблицы определить, что показывает стрелка Медведицы для полуночи данного дня;

2) вычесть из этого числа показание стрелки, определенное из наблюдений (если первое число меньше второго, то прибавить к первому 12 часов и после этого вычесть второе число);

3) полученное число удвоить.

Источник

Найти длительность периода белых ночей и продолжительность полярного дня и полярной ночи в Амдерме, географическая широта которой φ=+69°41′.

Данные: φ=+69°41’=+69°,7.

Решение. Подставляя в формулу (8) hн=-7° и φ=+69°,7, вычисляем склонение Солнца δ, при котором наступают белые ночи:

δ =h_н + (90°-φ) = -7°+(90°-69°,7) = + 13°,3.

Та же формула при h_н=-0°,9 дает для незаходяще-го Солнца δ = + 19°,4, а формула (4)—для невосходя-щего Солнца

δ = φ—z_в = 69°,7—90°,9 = — 21°,2.

По астрономическому календарю-ежегоднику устанавливаем, что Солнце имеет склонение δ = + 13°,3 26 апреля и 18 августа, δ= + 19°,4—18 мая и 27 июля, а δ = —21°,2 —28 ноября и 15 января.

Следовательно, в Амдерме с 26 апреля до 18 мая и с 27 июля до 18 августа длятся белые ночи, с 18 мая до 27 июля продолжается полярный день, а с 28 ноября до 15 января — полярная ночь.

Источник

Во время боевых операций часто бывает необходимо определять направления и время.

Определение направлений называется ориентировкой. Для ориентировки пользуются компасом. При обучении бойцов и командиров указывается, как пользоваться компасом. Однако, может случиться, что одиночный боец или группа бойцов окажется без компаса. Для определения времени служат часы. Однако, боец может оказаться без часов.

В этой книжке как раз для таких случаев даются способы, с помощью которых можно приблизительно определить направление без компаса и время без часов. В конце книжки даются дополнительные сведения о Луне и планетах, могущие оказаться полезными для той же цели.

Находясь во всяком месте, нужно уметь быстро найти стороны горизонта— север (С), юг (Ю), восток (В), запад (3).

Запомните твердо взаимное расположение сторон горизонта по рис. 1. Боец стоит лицом к югу с раскинутыми в стороны руками. Сзади будет север, справа будет запад, слева — восток. Достаточно определить направление на одну из сторон горизонта; остальные найдем, зная их взаимное расположение. Так, если повернуться лицом к северу, то юг окажется сзади, запад — слева, а восток — справа. Если встать липом к западу, сзади будет восток, справа — север, слева — юг. И наконец, если встать лицом к востоку, то сзади окажется запад, слева — север, справа — юг. Научитесь делать это быстро.

Рис. 1

Рис. 2

Промежуточные направления (рис. 2), лежащие между направлениями на север, на юг, на восток и на запад, называют так:

Направление посредине между севером и востоком называют северо- восточным направлением (СВ).
Направление посредине между востоком и югом называют юго-восточным направлением ЮВ).
Направление посредине между югом и западом называют юго-западным направлением (ЮЗ).
Направление посредине между западом и севером называют северо-западным направлением (СЗ).

Ориентировка около полудня. Каждый день ровно в 12 часов по солнечному времени Солнце бывает точно на юге. То время, по которому мы живем, которое показывают наши часы, это — не солнечное время. Для разных городов солнечное время по-разному отличается от времени, показываемого часами. В среднем наши часы идут на 1 час впереди солнечного времени. Поэтому по нашим часам Солнце бывает на юге не в 12 часов, а около 13 часов.

Следовательно, получается такое правило:

Если около 13 часов встать лицом к Солнцу, то впереди будет юг, справа — запад, слева — восток и сзади — север.

Когда, Солнце бывает на юге, оно стоит выше всего над горизонтом, и в это время тени от предметов самые короткие. Поэтому можно обойтись без часов и совершенно точно определить положение сторон горизонта, наблюдая за изменением длины тени какого-нибудь предмета.

Около 12 часов дня воткните в землю палку отвесно (вертикально). Проверьте правильность установки отвесом (груз, подвешенный на тонкой веревке). Следите за тенью палки и отмечайте время от времени положение тени колышком, камешком и т. п.; вы увидите, что тень поворачивается, и при этом сначала она будет укорачиваться, потом станет удлиняться.

Направление самой короткой тени есть направление точно на север (рис. 3).

Заметьте себе это направление по какому-нибудь предмету, стоящему далеко от вас (дом, дерево, кусты и т. п.).

Рис. 3 | Рис. 4

Если момент, когда тень была самой короткой, будет по какой-либо причине пропущен, то можно поступить так: отметьте два положения тени от отвесно стоящей палки — одно до полудня, другое после полудня, когда длина тени будет одинаковой. Направления на север лежат посредине между направлениями этих одинаковых теней (рис. 4).

Ориентировка по месту восхода и захода Солнца. Около 22 марта и около 22 сентября Солнце восходит на востоке и заходит на западе. Зимой (в декабре) Солнце восходит на юго-востоке и заходит на юго-западе. Летом (в июне) Солнце восходит на северо-востоке и заходит на северо-западе.

Зная это, можно найти стороны горизонта по месту восхода или захода Солнца. Чтобы запомнить это место горизонта, следует заметить какой-нибудь предмет, находящийся по направлению к месту восхода или захода.

Ориентировка по положению Солнца. Если у вас есть часы и видно Солнце, то можно воспользоваться следующим способом. Часы поворачивают так, чтобы часовая стрелка была направлена к Солнцу (рис. 5). Прямая, проведенная через центр циферблата и делящая пополам угол между часовой стрелкой и 1 часом на циферблате, показывает на юг.

Рис. 5

Для приближенной ориентировки по положению Солнца полезно запомнить следующее:

около 7 часов Солнце бывает на востоке;
около 10 часов Солнце бывает на юго-востоке;
около 13 часов Солнце бывает на юге;
около 16 часов Солнце бывает на юго-западе;
около 19 часов Солнце бывает па западе.

Примечание.

Зимой Солнце не бывает видно на востоке, так как оно восходит позже 7 часов, и не бывает видно на западе, так как оно заходит раньше 19 часов.

Ночью бывает видно много звезд. Если внимательно проследить за их восходом и заходом, за их движением относительно горизонта, то можно научиться ориентироваться по ним. Точнее всего ориентироваться по звездам можно так.

Найдите на небе созвездие Большой Медведицы, которое называют иногда Возом. Оно изображено на рис. 6. Это созвездие состоит из семи довольно ярких звезд, образующих фигуру, похожую на ковш.

Рис. 6

Обратите внимание на то, что в разное время ночи и в разные дни положение Большой Медведицы относительно поверхности Земли (относительно горизонта) может быть различным, но форма созвездия не меняется. На рис. 7 показано положение ковша Большой Медведицы для конца августа и начала сентября в 21 час, в 1 час и в 5 часов.

Рис. 7

Через две крайние звезды ковша Большой Медведицы (они обозначены на рис. 6 цифрами 1 и 2) проведите мысленно линию и продолжите ее на расстояние примерно в пять раз большее, чем расстояние между этими крайними звездами.

Вы найдете довольно яркую звезду, называемую Полярной. Смотрите ее на рис. 6 и 7.

Если встать лицом к Полярной звезде, то будем смотреть на север.

Отыскать Полярную звезду нетрудно, так как на линии между двумя крайними звездами Большой Медведицы и Полярной нет ярких звезд. Кроме того следует иметь в виду следующее:

Полярная звезда не меняет своего положения в течение всей ночи.
Чем севернее место на Земле, тем выше над горизонтом Полярная звезда.

Когда найдены стороны горизонта, то нужно уметь указать направление на любой предмет, находящийся где-нибудь в отдалении от вас.

Если стороны горизонта найдены приближенно, то достаточно указать, что предмет находится, например, на севере или на северо-западе. Если направление на предмет лежит между направлениями на север и на северо-запад, то такое направление называют северо-северо-западным (краткое обозначение ССЗ). Подобным же образом можно отмечать направления, расположенные между двумя другими смежными сторонами горизонта. Если же направление на стороны горизонта установлено достаточно надежно (например по Полярной звезде), то можно с большей точностью определить и угол между направлением на север (или любую другую сторону горизонта) и направлением на предмет.

Для глазомерной оценки углов можно пользоваться следующими способами.

Вытяните руку ладонью от себя: тогда ширина четырех пальцев у ладони представится углом в 7° (1—20 по счету углов в артиллерии).
Вытяните руку и раздвиньте возможно шире большой и указательный пальцы (рис. 8). Угол между направлениями на концы этих пальцев равен 15° (2—50 по счету углов в артиллерии).

Рис. 8

Чтобы воспользоваться вторым способом для глазомерного определения угла между направлением на север и направлением на предмет, направляем большой палец на север и смотрим, совпадает ли направление на указательный палец хотя бы приблизительно с направлением на предмет. Если да, то угол равен 15°. Пример показан на рис. 8. Если угол окажется больше или меньше 15°, то придется использовать и первый способ.

Требуется измерить угол между направлением на юг и направлением на окоп противника. Направляем большой палец вытянутой руки на юг, а конец указательного пальца в сторону окопа; окоп оказывается заметно правее. Это значит, что нужный нам угол больше 15°. На конце указательного пальца приходится отдаленное дерево. Передвигаем руку направо и наводим большой палец на дерево; смотрим на указательный палец, — окоп оказывается левее указательного пальца. Это значит, что угол между направлениями на дерево и окоп заметно меньше 15°.

Применяем первый способ. Наводим на дерево левый край ладони (правой руки) и смотрим на правый край. Если он закрывает окоп, то значит угол между направлениями на дерево и на окоп приблизительно равен 7°. Сложив 15° и 7°, получаем, что угол между направлением на юг и направлением на окоп приблизительно равен 22° (см. рис. 9).

Рис. 9

Примечания:

При таких оценках надо выбирать сторону горизонта, ближайшую к предмету.
Если один из углов окажется меньше 7°, то можно определить приблизительно, какую долю 7° он составляет.

Каждая звезда Большой Медведицы в течение суток описывает круг около Полярной звезды.

Прямую линию от Полярной звезды к звездам 1 и 2 Большой Медведицы будем для краткости называть стрелкой Медведицы.

Рис. 10

Когда звезды 1 и 2 стоят прямо под Полярной звездой, то стрелка направлена отвесно вниз. Условимся говорить, что она показывает 6 часов по условному счету. Это будет положение I на рис. 10^*. Продолжая наблюдение, мы скоро заметим, что в этом положении Большая Медведица движется вправо, т. е. к востоку, и медленно подымается по кругу, центром которого служит Полярная звезда. Через четверть суток, т. е. через 6 настоящих часов, стрелка Медведицы пройдет четверть оборота окружности, будет теперь располагаться не вертикально, а горизонтально, и мы получим положение II; ее стрелка показывает теперь 3 часа по условному счету и т. д.

_________
^*

Римские цифры I, II, III и IV на рис. 10 не имеют ничего общего с часами. Эти цифры обозначают «первое», «второе», «третье» и «четвертое» положения воображаемой стрелки описываемых «звездных часов».

Так как движение Большой Медведицы вокруг Полярной звезды совершается равномерно, то можно сказать, что Большая Медведица вместе с Полярной звездой — это условные звездные часы. Стрелкой у этих небесных часов служит воображаемая линия, проходящая от Полярной звезды к звездам 1 и 2 Большой Медведицы, но циферблата совсем нет. Но ведь циферблат и не особенно нужен. Когда мы смотрим на часы, мы очень часто определяем время просто по направлению стрелок и вовсе не стараемся рассмотреть цифру, на которую стрелка указывает.

Стрелка небесных часов поворачивается в направлении, обратном движению стрелки обычных часов. После положения II она будет проходить воображаемые цифры, соответствующие условным 2 ч., 1 ч., 12 ч., 11 ч. и т. д. Будем крепко помнить, что это не настоящие часы, а условные показания нашей воображаемой стрелки. Ниже описано, какие задачи можно решать с помощью этих воображаемых небесных часов.

3 а д а ч а 1.

Вообразим себе, что боец, не имеющий часов, вышел в ночную разведку, когда Большая Медведица еще не дошла до самого низкого положения (рис. 11). На-глаз он определил, что стрелка Медведицы стоит на 6¹/₂ условных часах. После выполнения задания он взглянул на Большую Медведицу и увидел, что ее стрелка показывала 4 условных часа. Сколько времени он провел в разведке?

Рис. 11

Для ответа на вопрос надо из 6¹/₂ часов вычесть 4 часа:

6¹/₂ часа — 4 часа=2¹/₂ часа (это — условные часы).

Для перевода условных часов в истинные нужно полученное число умножить на 2:

2¹/₂ условных часа Х 2=5 истинных часов.

Следовательно, разведка продолжалась приблизительно 5 часов.

З а д а ч а 2.

Сколько времени прошло, если в начале стрелка Медведицы показывала 2 условных часа (см. рис. 11), а в конце 10¹/₂ условных часов?

Чтобы из 2 часов можно было вычесть 10¹/₂, нужно сначала прибавить к 2 часам 12 часов:

2 условных часа +12 условных часов=14 условных часов.

Вычитаем:

14 условных час. — 10¹/₂ условных час.—3¹/₂ условных часа.

Для перевода условных часов в истинные, умножаем на 2:

3¹/₂ условных часа Х 2=7 истинных часов.

Отсюда получаем такое правило:

Чтобы по Большой Медведице определить, сколько времени прошло, надо:

заметить, сколько показывала стрелка Медведицы на воображаемых небесных часах вначале и в конце,
из первого числа вычесть второе (если первое число меньше второго, то прибавить к первому 12 и после этого вычесть второе),
полученное число умножить на два.

Эта задача труднее предыдущей потому, что звезды Большой Медведицы (как и все другие звезды) совершают полное обращение не ровно в 24 часа, а на 4 минуты скорее. Другими словами, наши звездные часы каждый день уходят вперед против обыкновенных часов на 4 минуты. Поэтому самое низкое положение Большой Медведицы (положение I на рис. 10) по обыкновенным часам завтра придется на 4 минуты раньше, чем было сегодня, послезавтра — на 8 минут раньше и так далее. Через месяц (через 30 дней) оно наступит раньше, чем сегодня, уже па 120 минут, т. е. на целых 2 часа. Несмотря на всю эту сложность, в названной задаче легко разобраться при помощи следующих сведений.

Около 22 сентября стрелка Медведицы в полночь (т. е. в 0 час. 00 мин. по нашим часам) направлена отвесно вниз и показывает на небесных часах 6 условных часов.

Числа эти нетрудно рассчитать и без таблички, если помнить первую строку и знать, что каждый месяц показание условных часов уменьшается на один условный час.

Решим, например, такую задачу:

З а д а ч а 3.

Как узнать по Большой Медведице, что наступила полночь 7 ноября?

7 ноября приходится посредине между 22 октября и 22 ноября. Поэтому из таблицы мы найдем, что в этот день в полночь стрелка Медведицы должна показывать 4¹/₂ условных часа. Значит, полночь наступит в то время, когда Большая Медведица займет положение как раз посредине между положением I (6 условных часов) и II (3 условных часа) на рис. 10.

З а д а ч а 4.

7 ноября стрелка Медведицы показывала 2 условных часа. Который час на самом деле?

В прошлой задаче мы уже определили из таблицы, что в полночь стрелка Медведицы 7 ноября показывает 4¹/₂ условных часа. Чтобы узнать искомое время, надо из 4¹/₂ условных часов вычесть 2 условных часа и результат умножить на 2:

4¹/₂ условных часа — 2 условных часа=2¹/₂ условных часа.

Умножив результат на 2, получим:

2¹/₂ условных часа Х 2=5 истинных часов (утра).

З а д а ч а 5.

20 октября стрелка Медведицы показывала 7 условных часов. Который час на самом деле?

5 условных часов+12 условных часов=17 условных часов;
17 условных часов—7 условных часов=10 условных часов.

Умножаем результат на 2:

10 условных часов Х 2=20 истинных часов (или 8 часов вечера).

Отсюда получаем такое правило:

Чтобы по положению стрелки Большой Медведицы узнать который час, надо:

из таблицы определить, что показывает стрелка Медведицы для полуночи данного дня;
вычесть из этого числа показание стрелки, определенное из наблюдений (если первое число меньше второго, то прибавить к первому 12 часов и после этого вычесть второе число);
полученное число удвоить.

Изменения вида Луны ученые называют сменой лунных фаз. Основные фазы Луны это — новолуние, первая четверть, полнолуние и последняя четверть. В новолуние Луна не видна. Через 2—3 дня после новолуния Луна в виде узкого серпа недолго видна на западе после захода Солнца. С каждым днем ширина серпа увеличивается, и Луна принимает вид половины кружка [) — это первая четверть. Еще через 7—8 дней Луна принимает вид полного кружка О— это полнолуние. Потом с правой стороны Луны появляется ущерб, который увеличивается и через 7—8 дней после полнолуния Луна снова принимает вид половинки кружка (] — это последняя четверть. Еще несколько дней Луна видна в виде серпа, обращенного выпуклостью налево, а затем наступает новолуние, после которого все фазы Луны повторяются вновь.

В полнолуние Луна восходит вечером, а заходит утром и, следовательно, она светит всю ночь. В первой четверти Луна видна в первой половине ночи (она заходит в середине ночи), а в последней четверти Луна видна во второй половине ночи (она восходит в середине ночи).

Осенью в первой четверти Луна поднимается невысоко над горизонтом и светит слабо. В последней четверти она поднимается высоко и ярко светит начиная с 22—23 часов. Зимой полная Луна поднимается очень высоко над горизонтом.

Каждый день восход и заход Луны и ее движение по небу происходят по-разному, и потому ориентироваться по Луне труднее, чем по Солнцу и звездам. Однако, бывают случаи, когда звезд не видно, а Луна просвечивает сквозь облака. Поэтому надо уметь хотя бы приближенно ориентироваться по Луне.

Для ориентировки по положению Луны служит следующая табличка, которая показывает, в котором часу (приблизительно) Луна бывает на востоке, на юге и на западе.

Продолжительность ночи считается от появления на небе ярких звезд до их исчезновения.

Продолжительность ночи меняется в течение года. Самая короткая ночь бывает летом — 22 июня, а самая длинная ночь бывает зимой — 22 декабря. Кроме того, продолжительность ночи разная для разных мест — зимой продолжительность ночи больше в том месте, которое расположено севернее (у которого широта, больше). В местностях, имеющих одинаковую широту, продолжительность ночи одинаковая.

В табличке приведены данные о продолжительности ночи в часах для широт 60° (Ленинград, Таллин, Выборг), 68° (Дно, Остров, Псков, Тарту), 64° (Смоленск, Орша, Могилев, Минск, Белосток), 50° (Киев, Житомир, Ровно, Львов), 46° (Одесса, Кишинев, Тирасполь). Эти данные годятся не только для названных городов, но и для других пунктов, имеющих близкую широту.

________

Настоящая брошюра составлена коллективом сотрудников Государственного астрономического института им. П. К. Штернберга в составе: проф. С. В. Орлова, проф. И. Ф. Полака, проф. Б. М. Щиголева и доц. П. Г. Куликовского под общей редакцией директора ГАИШ проф. Н. Д. Моисеева и преследует цель изложить простейшие способы астрономической ориентировки и приближенного определения времени, могущие оказаться полезными для бойцов Красной Армии и партизан.

Государственное издательство
Технико-Теоретической Литературы
МОСКВА 1941 ЛЕНИНГРАД

Источник

‍Полярный день

Условный счет звездных часов

Как по Большой Медведице узнать, сколько времени прошло?

Как по Большой Медведице узнать, что наступила полночь?

Как по Большой Медведице узнать, который час?

Не пропустите также: