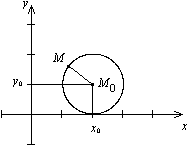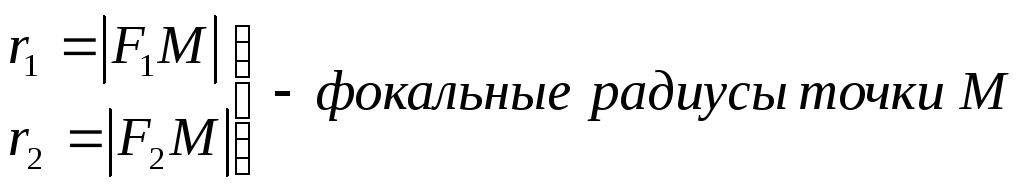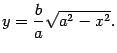Окружностью называется замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности). Расстояние от любой точки окружности (Pleft( right)) до ее центра называется радиусом . Центр окружности и сама окружность лежат в одной и той же плоскости. Уравнение окружности радиуса (R) с центром в начале координат ( каноническое уравнение окружности ) имеет вид
( + = ).
Уравнение окружности радиуса (R) с центром в произвольной точке (Aleft( right)) записывается как
( <left( right)^2> + <left( right)^2> = ).
Уравнение окружности, проходящей через три точки , записывается в виде: (left| <begin<*<20>> <+ > & x & y & 1\ & <> & <> & 1\ & <> & <> & 1\ & <> & <> & 1 end> right| = 0.\)
Здесь (Aleft( <,> right)), (Bleft( <,> right)), (Cleft( <,> right)) − три точки, лежащие на окружности.
Уравнение окружности в параметрической форме
( left < beginx &= R cos t \ y &= Rsin t end right., ;;0 le t le 2pi),
где (x), (y) − координаты точек окружности, (R) − радиус окружности, (t) − параметр.
Общее уравнение окружности
(A + A + Dx + Ey + F = 0)
при условии (A ne 0), (D^2 + E^2 > 4AF).
Центр окружности расположен в точке с координатами (left( right)), где
(a = — largefrac<<2A>>normalsize,;;b = — largefrac<<2A>>normalsize.)
Радиус окружности равен
(R = sqrt <largefrac<<+ — 4AF>><<2left| A right|>>normalsize> )
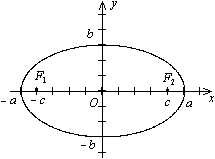
Эллипсом называется плоская кривая, для каждой точки которой сумма расстояний до двух заданных точек ( фокусов эллипса ) постоянна. Расстояние между фокусами называется фокусным расстоянием и обозначается через (2c). Середина отрезка, соединяющего фокусы, называется центром эллипса . У эллипса есть две оси симметрии: первая или фокальная ось, проходящая через фокусы, и перпендикулярная ей вторая ось. Точки пересечения этих осей с эллипсом называются вершинами . Отрезок, соединяющий центр эллипса с вершиной, называется полуосью эллипса . Большая полуось обозначается через (a), малая полуось − через (b). Эллипс, центр которого находится в начале координат, а полуоси лежат на координатных прямых, описывается следующим каноническим уравнением :
(largefrac<<>><<>>normalsize + largefrac<<>><<>>normalsize = 1.)
Сумма расстояний от любой точки эллипса до его фокусов постоянна:
( + = 2a),
где (), () − расстояния от произвольной точки (Pleft( right)) до фокусов () и (), (a) − большая полуось эллипса.
Соотношение между полуосями эллипса и фокусным расстоянием
( = + ),
где (a) − большая полуось эллипса, (b) − малая полуось, (c) − половина фокусного расстояния.
Уравнение эллипса в параметрической форме
( left < beginx &= acos t \ y &= bsin t end right., ;;0 le t le 2pi),
где (a), (b) − полуоси эллипса, (t) − параметр.
Общее уравнение эллипса
(A + Bxy + C + Dx + Ey + F = 0),
где ( — 4AC Общее уравнение эллипса, полуоси которого параллельны осям координат
(A + C + Dx + Ey + F = 0),
где (AC > 0).
Периметр эллипса
(L = 4aEleft( e right)),
где (a) − большая полуось эллипса, (e) − эксцентриситет, (E) − полный эллиптический интеграл второго рода.
Площадь эллипса
(S = pi ab)
Эллипс — определение и вычисление с примерами решения
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно Согласно определению эллипса имеем Из треугольников и по теореме Пифагора найдем
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим Раскроем разность квадратов Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно перейдет в уравнение Вновь возведем обе части равенства в квадрат Раскрывая все скобки в правой части уравнения, получим Соберем не- известные в левой части, а все известные величины перенесем в правую часть уравнения, получим Введем обозначение для разности, стоящей в скобках Уравнение принимает вид Разделив все члены уравнения на получаем каноническое уравнение эллипса: Если то эллипс вытянут вдоль оси Ох, для противоположного неравенства — вдоль оси Оу (при этом фокусы тоже расположены на этой оси). Проанализируем полученное уравнение. Если точка М(х; у) принадлежит эллипсу, то ему принадлежат и точки следовательно, эллипс симметричен относительно координатных осей, которые в данном случае будут называться осями симметрии эллипса. Найдем координаты точек пересечения эллипса с декартовыми осями:
- т.е. точками пересечения эллипса с осью абсцисс будут точки
- т.е. точками пересечения эллипса с осью ординат будут точки (Рис. 30).
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если то параметр а называется большой, а параметр b — малой полуосями эллипса.
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству Кроме того, эта характеристика описывает форму эллипса. Для демонстрации этого факта рассмотрим квадрат отношения малой полуоси эллипса к большой полуоси
Если и эллипс вырождается в окружность. Если и эллипс вырождается в отрезок
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр Зная параметр с, можно вычислить малую полуось эллипса Следовательно, каноническое уравнение заданного эллипса имеет вид:
Пример:
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса а третья вершина — в центре окружности
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
Следовательно, большая полуось эллипса а малая полуось Так как то эллипс вытянут вдоль оси ординат Оу. Определим расположение фокусов данного эллипса Итак, Окружность: Выделим полные квадраты по переменным Следовательно, центр окружности находится в точке О(-5; 1).
Построим в декартовой системе координат треугольник Согласно школьной формуле площадь треугольника равна Высота а основание Следовательно, площадь треугольника равна:
Эллипс в высшей математике
где и —заданные положительные числа. Решая его относительно , получим:
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное по абсолютной величине меньше , подкоренное выражение положительно, корень имеет два значения. Каждому значению , удовлетворяющему неравенству соответствуют два значения , равных по абсолютной величине. Значит, геометрическое место точек, определяемое уравнением (2), симметрично относительно оси . Так же можно убедиться в том, что оно симметрично и относительно оси . Поэтому ограничимся рассмотрением только первой четверти.
При , при . Кроме того, заметим, что если увеличивается, то разность уменьшается; стало быть, точка будет перемещаться от точки вправо вниз и попадет в точку . Из соображений симметрии изучаемое геометрическое место точек будет иметь вид, изображенный на рис. 34.
Полученная линия называется эллипсом. Число является длиной отрезка , число —длиной отрезка . Числа и называются полуосями эллипса. Число эксцентриситетом.
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом (рис. 35). В каждой из этих плоскостей возьмем систему координат, причем за ось примем прямую пересечения плоскостей, стало быть, ось будет общей для обеих систем. Оси ординат различны, начало координат общее для обеих систем. В плоскости возьмем окружность радиуса с центром в начале координат, ее уравнение .
Пусть точка лежит на этой окружности, тогда ее координаты удовлетворяют уравнению .
Обозначим проекцию точки на плоскость буквой , а координаты ее—через и . Опустим перпендикуляры из и на ось , это будут отрезки и . Треугольник прямоугольный, в нем , ,, следовательно, . Абсциссы точек и равны, т. е. . Подставим в уравнение значение , тогда cos
а это есть уравнение эллипса с полуосями и .
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей с коэффициентами деформации, равными
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам (х, у, z) с текущими координатами х, у, г, причем
Иными словами, линейные размеры сферы в направлении оси Ох уменьшаются в раз, если , и увеличиваются в раз, если и т. д.
Подставляя эти формулы в уравнение (1), будем иметь
где Уравнение (2) связывает текущие координаты точки М’ эллипсоида и, следовательно, является уравнением трехосного эллипсоида.
Величины называются полуосями эллипсоида; удвоенные величины называются осями эллипсоида и, очевидно, представляют линейные размеры его в направлениях деформации (в данном случае в направлениях осей координат).
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
окружность
Определение: Окружность — это линия второго порядка, которая представляет собой геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром.
Если центр находится в начале координат, то окружность задается каноническим уравнением второй степени вида: х2+у2=R2 , где R — радиус окружности; х,у — текущие координаты точек, лежащих на окружности.
Для вывода данного уравнения возьмем на окружности произвольную точку М(х;у). Отрезок ОМ=R является гипотенузой в прямоугольном треугольнике ОМР, а катеты определяются координатами х и у точки М. Уравнение окружности получается по теореме Пифагора: х2+у2=R2, которое называется каноническим уравнением окружности с несмещенным центром.
Если центр окружности находится в точке С(х0;у0), то уравнение окружности со смещенным центром будет иметь
Построение окружности выполняется с помощью циркуля.
эллипс
Определение: Эллипс — это линия второго порядка, которая представляет собой геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная и равная большой оси эллипса.
Эллипс с несмещенным центром задается каноническим уравнением второй степени вида:
где а и в — полуоси, х,у — текущие координаты точек, лежащих на эллипсе. Центр симметрии находится в начале координат. Осями симметрии служат координатные оси.
При рассмотрении эллипса возможны два случая:
- 1. Если ав, то а называется большая полуось, лежащая на координатной оси Ох, а в — малая полуось, лежащая на координатной оси Оу;
- 2. Если ав, то а называется малая полуось, лежащая на координатной оси Ох, а в-большая полуось, лежащая на координатной оси Оу.
Фокусы F1 и F2 всегда лежат на большой оси эллипса, причем симметрично относительно центра симметрии на расстоянии:
где величина «с» определяет фокусное расстояние.
Для характеристики формы эллипса вводится эксцентриситет.
Определение: Эксцентриситетом эллипса называется отношение фокусного расстояния к длине его большой полуоси:
=, если ав и =, если ва.
Значение эксцентриситета меняется в пределах 0??1. При этом форма эллипса изменяется от окружности (е=0, при а=в=R) и, вытягиваясь, вырождается в прямую (е=1, при а>>в).
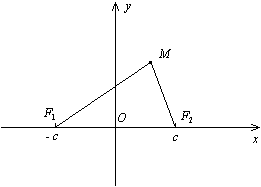
Уравнение эллипса выводится из его основного свойства, представленного в определении. Возьмём на эллипсе произвольную точку М(х;у). Расстояния r1 и r2 от фокусов F1 и F2 до точки М(х;у) называются фокальными радиусами.
В соответствии с определением сумма фокальных радиусов есть величина постоянная, равная большой оси эллипса: r1 + r2 = 2а (при ав) — основное свойство эллипса. Для вывода уравнения эллипса необходимо выразить фокальные радиусы r1 и r2 через координаты точки М(х;у) и фокусов F1(с;0) и F2(-с;0)и подставить в это равенство.
Если центр симметрии смещен и находится в точке С(х0;у0), то уравнение эллипса со смещенным центром имеет вид:
Построение эллипса рассмотрим ниже на примерах.
Пример. Определить вид, параметры и построить линию, заданную уравнением:
Решение: 1. Это эллипс с несмещенным центром вида:
2. Найдем параметры: — большая полуось на оси Ох;
— малая полуось на оси Оу;
Фокусы F1(4.6;0) и F2(-4.6;0) лежат на большой оси, совпадающей с осью Ох, симметрично, на расстоянии с=4.6 относительно начала координат.
- 3. Построение эллипса (см. рисунок выше) выполним по этапам:
- 1) строим систему координат Оху;
- 2) на координатных осях симметрично относительно начала координат откладываем большую и малую полуоси (а=5, в=2) и показываем вершины эллипса А1,А2,В1,В2;
- 3) через вершины эллипса параллельно координатным осям строим осевой прямоугольник;
- 4) вписываем эллипс в осевой прямоугольник;
- 5) на большой оси, совпадающей с осью Ох, симметрично относительно начала координат показываем фокусы F1(4.6;0) и F2(-4.6;0).
Алгебраической кривой второго порядка
называется линия, уравнение которой в
декартовой системе координат имеет вид
,
в котором А, В и С не могут быть одновременно
равны нулю, т.е.
.
1. Окружность и её уравнения.
Окружностью называется
геометрическое место точек, равноудалённых
от точки, называемой центром окружности.
Теорема Окружность радиуса Rс
центром в точкеMo(x0,y0)
имеет уравнение
(1)
Доказательство. Пусть
—
текущая точка окружности. По определению
окружности расстояние
равно
R(рис.1)
Рис.
1.Окружность
Выразив расстояние между точками
получим
Обе части уравнения неотрицательны.
Поэтому после возведения их в квадрат
получим эквивалентное уравнение
Пример1 Определить координаты
центра и радиус окружности
.
Решение. Выделив полные квадраты,
получим
Итак, центр окружности —
,
радиус равен 2
Эллипс
Эллипсом называется геометрическое
место точек плоскости, для каждой из
которых сумма расстояний до двух данных
точек той же плоскости, называемых
фокусами эллипса, есть величина
постоянная.
В отличие от окружности, записать в
«удобном» виде уравнение эллипса
в произвольной системе координат не
удается. Поэтому для фиксированного
эллипса приходится подбирать систему
координат так, чтобы его уравнение было
достаточно простым.
Пусть F1
и F2—
фокусы эллипса. Начало т.О
системы координат расположим на
середине отрезка
.
Ось
направим
вдоль этого отрезка, ось —
перпендикулярно к этому отрезку.
т.
,
т.
,
Тогда по определению эллипса
Перенесем один из корней вправо и обе
части возведем в квадрат:
После того, как раскроем скобки и приведем
подобные члены, приходим к выражению
Разделим обе части этого уравнения на
4 и возведем в квадрат
Раскроем скобку и приведем подобные
члены
Учитывая, что
,
имеем равенство
Наконец, разделив обе части на
,
получим уравнение
(2)
Уравнение(2) называется каноническим
уравнением эллипса.
Исследование полученного уравнения
показывают:
-
Эллипс имеет оси симметрии (Ох, Оу);
-
начало координат- центр симметрии
Проведем построение эллипса, заданного
уравнением (2). Заметим, что из-за симметрии
достаточно нарисовать часть эллипса,
лежащую в верхней полуплоскости.
Уравнение этой линии мы получим, выразив
у из уравнения
(2)
и взяв перед корнем знак «+»,
Построим график этой функции. Область
определения — отрезок
,
y(0) = b, при
увеличении переменного
от
0 до
функция
монотонно убывает. В силу симметрии
графика относительно оси
функция
y
монотонно растет при изменении
от
–a
до 0. Производная
определена во всех точках интервала
и, следовательно, график является
гладким (не содержит изломов, касательная
есть в любой точке). Вторая производная
отрицательна во всех точках интервала
,
следовательно, график — выпуклый вверх.
Осталось не исследованным поведение
кривой вблизи концов отрезка
.
Выразим из уравнения (2)
переменное
через
y:
.
Очевидно, что в точке y
= 0 эта функция имеет производную,
то есть касательная к этому графику в
точке
существует. Легко проверить, что она
параллельна оси Oy.
Из симметрии эллипса делаем вывод, что
это гладкая кривая и строим ее с учетом
полученных данных (рис. 3).
Рис.3.Эллипс
Точки пересечения эллипса с его осями
симметрии называются вершинами
эллипса, центр симметрии центром
эллипса, отрезок между двумя вершинами,
содержащий фокусы, называется большой
осью эллипса, половина его длины —
большой полуосью эллипса. Отрезок
между вершинами на оси симметрии, не
содержащей фокусов, называется малой
осью эллипса, половина его длины —
малой полуосью. . Величина
,
являющаяся половиной расстояния между
фокусами, определяется из формулы (12.5)
для величины
,
а именно,
(3).
Величина
называется эксцентриситетом
эллипса. Эксцентриситет
эллипса
характеризует степень вытянутости
эллипса. Чем ближе эксцентриситет к
нулю, тем больше эллипс похож на
окружность. Чем ближе эксцентриситет
к 1, тем сильнее вытянут эллипс. Отметим,
что по определению для эллипса
.
Пример 2 Постройте кривую
.
Найдите фокусы и эксцентриситет.
Решение. Разделим обе части уравнения
на 36. Получаем уравнение
Это — каноническое уравнение эллипса,
,
.
Делаем чертеж (рис. 4)
Рис.4.Эллипс,
заданный уравнением
Из соотношения (3)
находим
,
.
Фокусы —
,
,
эксцентриситет —
.
Пример 3 Построить эллипс
.
Найти его фокусы и эксцентриситет.
Решение. Уравнение запишем в виде
Это уравнение не является каноническим
уравнением эллипса, так как в соответствии
с уравнением (2)
в нем
,
,
,
а должно быть
.
Однако, если переобозначить оси, то есть
положить
,
,
то уравнение (2)
в координатах
примет
вид
Это — каноническое уравнение эллипса
при
,
.
Делаем чертеж (рис. 5).
Рис.12.8.Эллипс,
заданный уравнением
Из соотношения (3)
находим
.
Значит, фокусы в системе координат
имеют координаты
,
,
а в системе координат
— координаты,
.
Эксцентриситет равен
.
Из примера 3 ясно, что построение кривой
(эллипса) с уравнением (2)
при
можно
вести так же, как и для эллипса, заданного
каноническим уравнением: отложить
полуось
на
оси
,
полуось
—
на оси Оу и
через получившиеся вершины провести
эллипс. Различие заключается в том, что
фокусы теперь располагаются на оси
ординат (большой оси), величину
нужно
вычислять по формуле
,
и
.
Соседние файлы в папке модуль2
- #
- #
- #
Уравнение линии второго порядка:

Рассмотрим некоторые виды линий второго порядка.
1. Окружность – это геометрическое место точек, равноудаленных от данной точки, называемой центром.
В случае окружности уравнение 4.15 примет вид:

Если центр окружности находится в точке 


Если центр окружности находится в точке 


Например, запишем уравнение окружности с центром в точке 


2. Эллипс – это геометрическое место точек, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная. Расстояние от точки эллипса до фокуса называют фокальным радиусом.
На рисунке 4.3 изображен эллипс: точка 







Каноническое уравнение эллипса:

где 

Фокусы имеют координаты


где

Эксцентриситет эллипса находят по формуле:

3. Гипербола – это геометрическое место точек, для каждой из которых модуль разностей расстояний до двух данных точек, называемых фокусами, есть величина постоянная.
На рисунке 4.4 изображена гипербола: точки 






Каноническое уравнение гиперболы:

где 

Фокусы имеют координаты 


Эксцентриситет гиперболы находят по формуле:

Уравнения асимптот гиперболы:

4. Парабола – это геометрическое место точек, равноудаленных от фокуса и прямой, называемой директрисой.
Каноническое уравнение параболы:

где ось 


Фокус имеет координаты:

Уравнение директрисы параболы имеет вид:

Если осью симметрии параболы является ось 

В этом случае фокус имеет координаты:

Уравнение директрисы 

Пример 1. Найдите большую и меньшую полуоси, фокусы и эксцентриситет эллипса 
Решение. 1. С учетом 4.18, зная, что 



2. По формуле 4.19.1 получим: 


3. По формуле 4.20 найдем эксцентриситет: 
Пример 2. Найдите действительную и мнимую полуоси, фокусы, эксцентриситет и асимптоты гиперболы 
Решение. 1. С учетом 4.21, зная, что 



2. По формуле 4.22 получим: 


3. По формуле 4.23 найдем эксцентриситет: 
4. По формуле 4.24 запишем уравнения асимптот: 
Пример 3. Найдите фокус и директрису параболы 
Решение. С учетом 4.25, так как 



Пример 4. Найдите фокус и директрису параболы 
Решение. С учетом 4.26, так как 




1. Окружность.
Окружностью называется геометрическое место точек плоскости, равноудаленных от одной и той же точки этой плоскости (рис.1).
Рис.1
Уравнение окружности с центром в точке (а;b) и радиусом r имеет вид:
В частном случае, когда центр окружности лежит в начале координат, ее уравнением является
Общее уравнение кривой второго порядка
представляет окружность, если коэффициенты при квадратах координат равны между собой, А=С, и если отсутствует член с произведением координат ху, т.е. В=0.
2. Эллипс.
Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, равная 2а.
Каноническое уравнение эллипса имеет вид:
Координаты фокусов эллипса F(с;0) и F₁(-с;0). Расстояние между фокусами эллипса равно 2с. Точки пересечения эллипса с осями координат А(а;0), А₁(-а;0), B(0;b), B₁(0;-b) — называются вершинами.
Отрезки AA₁=2a, BB₁=2b называются осями эллипса. Эксцентриситет эллипса
Расстояния r и r₁ точки М(х;у) эллипса до его фокусов называются фокальными радиусами этой точки и определяются формулами
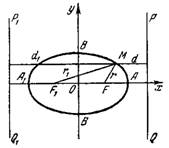
Две прямые PQ и P₁Q₁, параллельные малой оси эллипса и отстоящие от нее на расстоянии a/e называются директрисами эллипса. Их уравнения:
или
Отношение расстояний любой точки эллипса до фокуса и соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса:
Уравнение эллипса с осями, параллельными координатным осям, имеет вид
где (x₀,y₀) — координаты центра эллипса.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Эллипс.
Эллипс с каноническим уравнением $frac{x^2}{a^2}+frac{y^2}{b^2}=1, ageq b>0,$ имеет форму изображенную на рисунке.
Параметры $a$ и $b$ называются полуосями эллипса (большой и малой соответственно). Точки $A_1(-a, 0),$ $A_2(a, 0), $ $B_1(0, -b), $ и $B_2(0, b), $ его вершинами. Оси симметрии $Ox$ и $Oy$ — главными осями а центр симметрии $O -$ центром эллипса.
Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt{a^2-b^2}geq 0,$ называются фокусами эллипса векторы $overline{F_1M}$ и $overline{F_2M} -$ фокальными радиус-векторами, а числа $r_1=|overline{F_1M}|$ и $r_2=|overline{F_2M}| -$ фокальными радиусами точки $M,$ принадлежащей эллипсу. В частном случае $a=b$ фокусы $F_1$ и $F_2$ совпадают с центром, а каноническое уравнение имеет вид $frac{x^2}{a^2}+frac{y^2}{a^2}=1,$ или $x^2+y^2=a^2,$ т.е. описывает окружность радиуса $a$ с центром в начале координат.
Число $e=frac{c}{a}=sqrt{1-frac{b^2}{a^2}} ,, (0leq e<1)$ называется эксцентриситетом эллипса и является мерой его «сплюснутости» (при $e=0$ эллипс является окружностью.)
Прямые $D_1: x=-a/e$ и $D_2: x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами эллипса.
Теорема. (Директориальное свойство эллипса)
Эллипс является множеством точек, отношение расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно $e.$
Примеры.
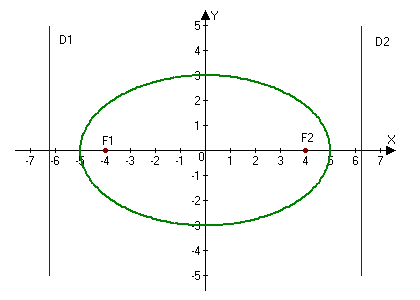
2.246. Построить эллипс $9x^2+25y^2=225.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.
Решение.
Приведем уравнение эллипса к каноническому виду:
$$ 9x^2+25y^2=225 |:225Rightarrowfrac{9x^2}{225}+frac{25y^2}{225}=1Rightarrow$$
$$Rightarrowfrac{x^2}{25}+frac{y^2}{9}=1Rightarrowfrac{x^2}{5^2}+frac{y^2}{3^2}=1.$$
а) Находим полуоси $a=5,$ $b=3.$
б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt{a^2-b^2}:$
$c=sqrt{5^2-3^2}=sqrt{16}=4Rightarrow F_1(-4, 0),qquad F_2(4, 0).$
в) Эксцентриситет $e=frac{c}{a}=frac{4}{5}.$
г) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac{5}{4/5}=-frac{25}{4}$ и $D_2: x=frac{5}{4/5}=frac{25}{4}.$
Сделаем рисунок:
Ответ: а) $a=5,$ $b=3;$ б) $ F_1(-4, 0),qquad F_2(4, 0);$ в) $e=frac{4}{5};$ г) $D_1: x=-frac{25}{4}$ и $D_2: x=frac{25}{4}.$
{jumi[*3]}
2.249 (a). Установить, что уравнение $5x^2+9y^2-30x+18y+9=0$ определяет эллипс, найти его центр $C,$ полуоси, эксцентриситет и уравнения директрис.
Решение.
Приведем уравнение эллипса к каноническому виду, для этого выделим полные квадраты:
$$5x^2+9y^2-30x+18y+9=(5x^2-30x)+(9y^2+18y)+9=$$
$$5(x^2+6x+9-9)+9(y^2+2y+1-1)+9=5(x+3)^2-45+9(y+1)^2-9+9=$$
$$5(x+3)^2+9(y+1)^2-45=0Rightarrow5(x+3)^2+9(y+1)^2=45|:45Rightarrow$$
$$ frac{(x+3)^2}{9}+frac{(y+1)^2}{5}=1Rightarrowfrac{(x+3)^2}{3^2}+frac{(y+1)^2}{(sqrt 5)^2}=1.$$
Это уравнение эллипса. Центр имеет координаты $C=(x_0, y_0)=(-3, -1);$ полуоси $a=3,$ $b=sqrt 5.$
$c=sqrt{a^2-b^2}Rightarrow c=sqrt{9-5}=sqrt 4=2Rightarrow e=frac{c}{a}=frac{2}{3}.$
Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac{3}{2/3}=-frac{9}{2} $ и $D_2: x=frac{3}{2/3}=frac{9}{2}.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$
$$D_1: x=3-frac{9}{2}=frac{6-9}{2}=-frac{3}{2}Rightarrow 2x+3=0 $$ $$D_2: x=3+frac{9}{2}=frac{6+9}{2}=frac{15}{2}Rightarrow2x-15=0.$$
Ответ: $C=(x_0, y_0)=(-3, -1);$ $a=3,$ $b=sqrt 5;$ $ e=frac{2}{3}.$ $D_1:2x+3=0, $ $D_2: 2x-15=0.$
2.252. Эллипс, главные оси которого совпадают с координатными осми, проходят через точки $M_1(2, sqrt 3)$ и $M_2(0, 2).$ Написать его уравнение, найти фокальные радиусы точки $M_1$ и расстояния этой точки до директрис.
Решение.
Поскольку оси эллипса совпадают с координатными осями, то центр эллипса совпадает с началом координат. Следовательно, из того, что точка $(0, 2)$ принадлежит эллипсу, можно сделать вывод, что $b=2.$
Далее, чтобы найти $a,$ подставим найденное значение $b$ и координаты точки $M_1(2, sqrt 3)$ в каноническое уравнение эллипса $frac{x^2}{a^2}+frac{y^2}{b^2}=1:$
$$frac{2^2}{a^2}+frac{(sqrt 3)^2}{2^2}=1Rightarrow frac{4}{a^2}+frac{3}{4}=1Rightarrow frac{4}{a^2}=frac{1}{4}Rightarrow a^2=16Rightarrow a=4.$$
Таким образом, уравнение эллипса $frac{x^2}{16}+frac{y^2}{4}=1.$
Далее найдем координаты фокусов:
$c=sqrt{a^2-b^2}=sqrt{16-4}=2sqrt 3Rightarrow F_1(-2sqrt 3, 0),,,, F_2(2sqrt 3, 0).$
Отсюда находим $overline {F_1M_1}=(2+2sqrt 3, sqrt 3),$ $overline{F_2M_1}=(2-2sqrt 3, sqrt 3).$
Соответственно, $r_1=|overline {F_1M_1}|=sqrt{(2+2sqrt 3)^2+ (sqrt 3)^2}=sqrt{4+8sqrt 3+12+3}=$ $=sqrt{16+8sqrt 3+3}=sqrt{(4+sqrt 3)^2}=4+sqrt 3,$
$r_2=|overline {F_2M_1}|=sqrt{(2-2sqrt 3)^2+ (sqrt 3)^2}=sqrt{4-8sqrt 3+12+3}=$ $=sqrt{16-8sqrt 3+3}=sqrt{(4-sqrt 3)^2}=4-sqrt 3.$
Чтобы найти расстояния от точки $M_1$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$e=frac{c}{a}=frac{2sqrt 3}{4}=frac{sqrt 3}{2};$
$D_1: x=-frac{4}{frac{sqrt 3}{2}}=-frac{8}{sqrt 3}Rightarrow sqrt 3 x+8=0;$
$D_2: x=frac{4}{frac{sqrt 3}{2}}=frac{8}{sqrt 3}Rightarrow sqrt 3 x-8=0.$
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac{Ax_0+By_0+C}{sqrt{A^2+B^2}}right|.$$
Таким образом, расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_1: sqrt 3 x+8=0$
$$d_1=left|frac{2sqrt 3+8}{sqrt{(sqrt 3)^2}}right|=frac{2sqrt 3+8}{sqrt 3};$$
расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_2: sqrt 3 x-8=0$
$$d_2=left|frac{2sqrt 3-8}{sqrt{(sqrt 3)^2}}right|=frac{8-2sqrt 3}{sqrt 3}.$$
Ответ: $frac{x^2}{16}+frac{y^2}{4}=1,$ $r_1=4+sqrt 3,$ $r_2=4-sqrt 3,$ $d_1=frac{8+2sqrt 3}{sqrt 3},$ $d_2=frac{8-2sqrt 3}{sqrt 3}.$
Гипербола.
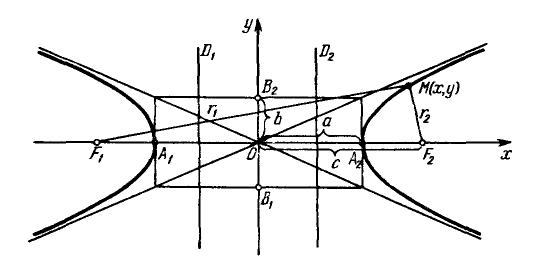
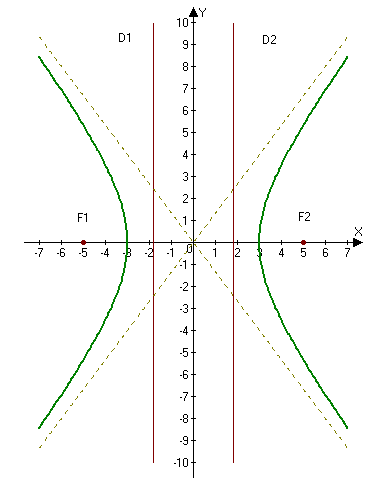
Гипербола с каноническим уравнением $frac{x^2}{a^2}-frac{y^2}{b^2}=1, a,b>0,$ имеет форму изображенную на рисунке.
Параметры $a$ и $b$ называются полуосями гиперболы. Точки $A_1(-a, 0),$ $A_2(a, 0) — $ ее вершинами. Оси симметрии $Ox$ и $Oy$ — действительной и мнимой осями а центр симметрии $O -$ центром гиперболы.
Прямые $y=pmfrac{b}{a}x$ являются асимптотами гиперболы.
Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt{a^2+b^2}geq 0,$ называются фокусами гиперболы, векторы $overline{F_1M}$ и $overline{F_2M} -$ фокальными радиус-векторами, а числа $r_1=|overline{F_1M}|$ и $r_2=|overline{F_2M}| -$ фокальными радиусами точки $M,$ принадлежащей гиперболе.
Число $e=frac{c}{a}=sqrt{1+frac{b^2}{a^2}} ,, (1<e<+infty)$ называется эксцентриситетом гиперболы и является мерой ее «сплюснутости». В частном случае $a=b$ гипербола называется равносторонней; ее эксцентриситет равен $e=sqrt{2},$ а угол между асимптотами равен $pi/2.$
Прямые $D_1: x=-a/e$ и $D_2:x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами гиперболы.
Теорема. (Директориальное свойство гиперболы).
Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно $e.$
Примеры.
2.265. Построить гиперболу $16x^2-9y^2=144.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.
Решение.
Приведем уравнение гиперболы к каноническому виду:
$$ 16x^2-9y^2=144 |:144Rightarrowfrac{16x^2}{144}-frac{9y^2}{144}=1Rightarrow$$
$$Rightarrowfrac{x^2}{9}-frac{y^2}{16}=1Rightarrowfrac{x^2}{3^2}+frac{y^2}{4^2}=1.$$
а) Находим полуоси $a=3,$ $b=4.$
б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt{a^2+b^2}:$
$c=sqrt{3^2+4^2}=sqrt{25}=5Rightarrow F_1(-5, 0),qquad F_2(5, 0).$
в) Эксцентриситет $e=frac{c}{a}=frac{5}{3}.$
г) Асимптоты гиперболы находим по формулам $y=pmfrac{b}{a}x:$
$$y=pmfrac{4}{3}x.$$
д) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac{3}{5/3}=-frac{9}{5}$ и $D_2: x=frac{3}{5/3}=frac{9}{5}.$
Сделаем рисунок:
Ответ: а) $a=3,$ $b=4;$ б) $ F_1(-5, 0),qquad F_2(5, 0);$ в) $e=frac{5}{3};$ г) $y=pmfrac{4}{3}x;$ д) $D_1: x=-frac{9}{5}$ и $D_2: x=frac{9}{5}.$
2.269 (a). Установить, что уравнение $16x^2-9y^2-64x-54y-161=0$ определяет гиперболу, найти ее центр $C,$ полуоси, эксцентриситет, уравнения асимптот и директрис.
Решение.
Приведем заданное уравнение к каноническому виду, для этого выделим полные квадраты:
$$16x^2-9y^2-64x-54y-161=(16x^2-64x)-(9y^2+54y)-161=$$
$$16(x^2-4x+4-4)-9(y^2+6y+9-9)-161=16(x-2)^2-64-9(y+3)^2+81-161=$$
$$16(x-2)^2-9(y+3)^2-144=0Rightarrow16(x-2)^2-9(y+3)^2=144|:144Rightarrow$$
$$ frac{(x-2)^2}{9}-frac{(y+3)^2}{16}=1Rightarrowfrac{(x-2)^2}{9}-frac{(y+3)^2}{16}=1.$$
Это уравнение гиперболы. Центр имеет координаты $C=(x_0, y_0)=(2,-3);$ полуоси $a=3,$ $b=4.$
$c=sqrt{a^2+b^2}Rightarrow c=sqrt{9+16}=sqrt {25}=5Rightarrow e=frac{c}{a}=frac{5}{3}.$
Асимптоты гиперболы c центром в начале координат, находим по формулам $y=pmfrac{b}{a}x,$ а с центром в точке $C=(x_0, y_0) -$ по формуле $y-y_0=pmfrac{b}{a}(x-x_0),$
$$y+3=frac{4}{3}(x-2)Rightarrow 3y+9=4x-8Rightarrow 4x-3y-17=0.$$
$$y+3=-frac{4}{3}(x-2)Rightarrow 3y+9=-4x+8Rightarrow 4x+3y+1=0.$$
Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac{3}{5/3}=-frac{9}{5} $ и $D_2: x=frac{3}{5/3}=frac{9}{5}.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$
$$D_1: x=2-frac{9}{5}=frac{10-9}{5}=frac{1}{5}Rightarrow 5x-1=0 $$
$$D_2: x=2+frac{9}{5}=frac{10+9}{5}=frac{19}{5}Rightarrow 5x-19=0 $$
Ответ: $C=(2, -3);$ $a=3,$ $b=4;$ $ e=frac{5}{3},$ $4x-3y-17=0,$ $4x+3y+1=0,$ $D_1:5x-1=0, $ $D_2: 5x-19=0.$
2.272. Убедившись, что точка $M(-5, 9/4)$ лежит на гиперболе $frac{x^2}{16}-frac{y^2}{9}=1,$ найти фокальные радиусы этой точки и расстояния этой точки до директрис.
Решение.
Проверим, что заданная точка лежит на гиперболе:
$$frac{x^2}{16}-frac{y^2}{9}=1Rightarrow frac{(-5)^2}{16}-frac{(9/4)^2}{9}=frac{25}{16}-frac{81}{16cdot 9}=frac{25cdot 9-81}{144}=frac{144}{144}=1.$$
Следовательно, точка $M(-5, 9/4)$ лежит на гиперболе $frac{x^2}{16}-frac{y^2}{9}=1.$
Для того, чтобы найти фокальные радиусы, найдем фокусы гиперболы:
$c=sqrt{a^2+b^2}Rightarrow c=sqrt{16+9}=sqrt {25}=5$ Следовательно, фокусы имеют координаты $F_1(-5, 0), F_2(5, 0).$
Фокальные радиусы точки, можно найти по формулам $r_1=|overline{F_1M}|$ и $r_2=|overline{F_2M}|.$
$$overline{F_1M}=(-5-(-5), 9/4)=(0, 9/4)Rightarrow |overline{F_1M}=sqrt{(9/4)^2}|=9/4.$$
$$overline{F_2M}=(-5-5, 9/4)=(-10, 9/4)Rightarrow |overline{F_1M}=sqrt{10^2+(9/4)^2}|=$$ $$=sqrt{100+81/16}=sqrtfrac{1681}{16}=frac{41}{4}.$$
Чтобы найти расстояния от точки $M$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$e=frac{c}{a}=frac{5}{4};$
$D_1: x=-frac{4}{5/4}Rightarrow x=-frac{16}{5}Rightarrow 5x+16=0;$
$D_2: x=frac{4}{5/4}Rightarrow x=frac{16}{5}Rightarrow 5x-16=0;$
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac{Ax_0+By_0+C}{sqrt{A^2+B^2}}right|.$$
Таким образом, расстояние от точки $M(5, 9/4)$ до прямой $D_1: sqrt 5x+16=0$
$$d_1=left|frac{5cdot 5+16}{sqrt{5^2}}right|=frac{41}{5};$$
расстояние от точки $M(5, 9/4)$ до прямой $D_2: sqrt 5x-16=0$
$$d_2=left|frac{5cdot 5-16}{sqrt{5^2}}right|=frac{9}{5}.$$
Ответ: $r_1=9/4,$ $r_2=frac{41}{4};$ $d_1=frac{41}{5};$ $d_2=frac{9}{5}.$
2.273. Найти точки гиперболы $frac{x^2}{9}-frac{y^2}{16}=1,$ находящиеся на расстоянии $7$ от фокуса $F_1.$
Решение.
Из уравнения гиперболы находим полуоси: $a=3, , b=4.$ Следовательно, $c=sqrt{a^2+b^2}Rightarrow c=sqrt{9+16}=sqrt {25}=5.$
Отсюда находим $F_1=(-5, 0).$
Геометрическое место точек, расположенных на расстоянии $7$ от фокуса $F_1,$ это окружность с центром в точке $F_1=(-5, 0)$ и радиусом $r=7:$
$$(x+5)^2+y^2=7^2.$$
Чтобы найти точки гиперболы $frac{x^2}{9}-frac{y^2}{16}=1,$ находящиеся на расстоянии $7$ от фокуса $F_1,$ решим систему уравнений
$$left{begin{array}{lcl}frac{x^2}{9}-frac{y^2}{16}=1\(x+5)^2+y^2=7^2end{array}right.$$
$$Rightarrowleft{begin{array}{lcl}frac{x^2}{9}-frac{y^2}{16}=1\y^2=7^2-(x+5)^2end{array}right.Rightarrowleft{begin{array}{lcl}frac{x^2}{9}-frac{7^2-(x+5)^2}{16}=1\y^2=7^2-(x+5)^2end{array}right.$$
$$Rightarrowleft{begin{array}{lcl}16x^2-9(49-x^2-10x-25)=144\y^2=7^2-(x+5)^2end{array}right.Rightarrow$$ $$Rightarrowleft{begin{array}{lcl}16x^2-216+9x^2+90x=144\y^2=7^2-(x+5)^2end{array}right.Rightarrow$$
$$Rightarrowleft{begin{array}{lcl}25x^2+90x-360=0\y^2=7^2-(x+5)^2end{array}right.Rightarrowleft{begin{array}{lcl}5x^2+18x-72=0\y^2=7^2-(x+5)^2end{array}right.$$
Решим уравнение $5x^2+18x-72=0:$
$D=18^2+4cdot5cdot72=324+1440=1764=42^2.$
$x_1=frac{-18+42}{10}=frac{24}{10}=2,4;$ $x_2=frac{-18-42}{10}=-6.$
Находим соответствующие координаты $y:$ $y_1=pmsqrt{24-2,4^2-10cdot 2,4}=sqrt{-5,76}$ — нет корней.
$y_2=pmsqrt{24-6^2+10cdot5}=pm4sqrt{3}.$
Ответ: $(-6, pm4sqrt 3).$
Парабола.
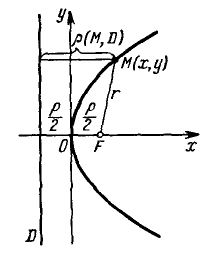
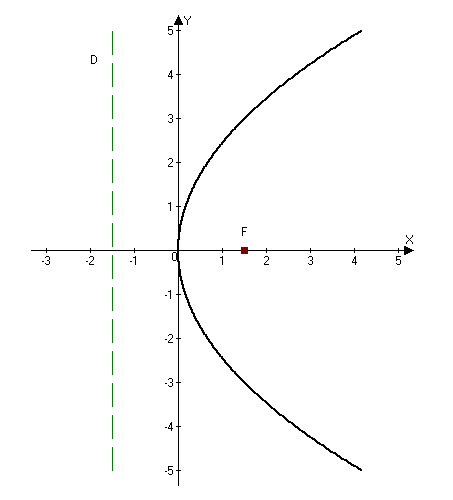
Парабола с каноническим уравнением $y^2=2px, p>0,$ имеет форму изображенную на рисунке.
Число $p$ называется параметром параболы. Точка $O -$ ее вершиной, а ось $Ox$ — осью параболы.
Точка $Fleft(frac{p}{2}, 0right)$ называется фокусом параболы, вектор $overline{FM} -$ фокальным радиус-векторам, а число $r=|overline{FM}| -$ фокальным радиусом точки $M,$ принадлежащей параболе.
Прямая $D: x=-p/2$ перпендикулярная оси и проходящая на расстоянии $p/2$ от вершины параболы, называется ее директрисой.
Примеры.
2.285 (а). Построить параболу $y^2=6x$ и найти ее параметры.
Решение.
Параметр $p$ параболы можно найти из канонического уравнения $y^2=2px: $
$$y^2=6xRightarrow y^2=2cdot 3xRightarrow p=2.$$
Сделаем рисунок:
Ответ: $p=3.$
{jumi[*4]}
2.286 (а). Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси $Ox$ и $p=1/2.$
Решение.
Поскольку парабола расположена в левой полуплоскости, симметрично относительно оси $Ox,$ то уравнение параболы будет иметь вид $y^2=-2px.$ Подставляя заданное значение параметра, находим уравнение параболы:
$$y^2=-2cdotfrac{1}{2}x=-x.$$
Ответ: $y^2=-x.$
2.288 (а). Установить, что уравнение $y^2=4x-8$ определяет параболу, найти координаты ее вершины $A$ и величину параметра $p.$
Решение.
Уравнение параболы, центр которой сдвинут в точку $(x_0, y_0),$ имеет вид $(y-y_0)^2=2p(x-x_0)^2.$
Приведем заданное уравнние к такому виду:
$y^2=4(x-2).$
Таким образом, $y^2=4(x^2-2)$ — парабола с центром в точке $(0, 2).$ Параметр $p=2.$
Ответ: $C(0, 2),$ $p=2.$
2.290. Вычислить фокальный параметр точки $M$ параболы $y^2=12x,$ если $y(M)=6.$
Решение.
Чтобы найти фокальный параметр точки $M,$ найдем ее координаты. Для этого подставим в уравнение параболы координату $y:$ $$6^2=12xRightarrow 36=12xRightarrow x=3.$$
Таким образом, точка $M$ имеет координаты $(3, 6).$
Из уравнения параболы $y^2=12x$ находим параметр параболы: $y^2=2cdot 6xRightarrow p=6.$ Следовательно фокус параболы имеет координаты $F(3, 0).$
Далее находим фокальный параметр точки:
$r=|FM|=sqrt{(3-3)^2+(6-0)^2}=6.$
Ответ: $6.$
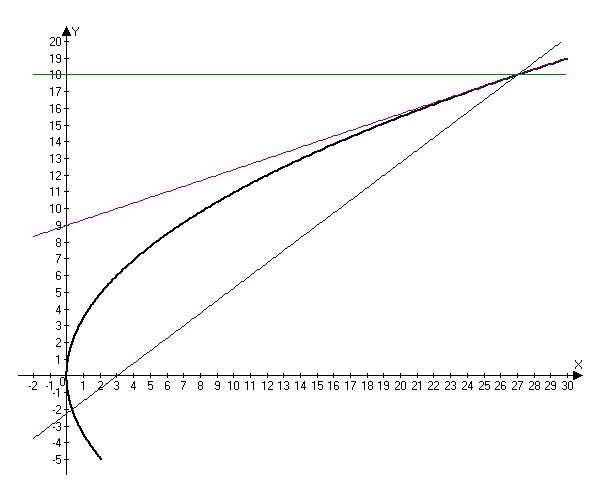
2.298. Из фокуса параболы $y^2=12x$ под острым углом $alpha$ к оси $Ox$ направлен луч света, причем $tgalpha=frac{3}{4}.$ Написать уравнение прямой, на которой лежит луч, отраженный от параболы.
Решение.
Найдем координаты фокуса. Из канонического уравнения параболы $y^2=2px$ находим параметр: $y^2=12x=2cdot 6xRightarrow p=6.$
Координаты фокуса $F(p/2, 0)Rightarrow F(3,0).$
Далее находим уравнение прямой, которая проходит через точку $(3, 0)$ под углом $alpha: tgalpha=frac{3}{4}$ к оси $OX.$ Уравнение ищем в виде $y=kx+b,$ где $k=tgalpha=frac{3}{4}.$
$y=frac{3}{4}x+b$
Чтобы найти $b,$ в уравнение прямой подставим координаты точки $(3, 0):$
$0=frac{3}{4}cdot 3+bRightarrow b=-frac{9}{4}.$ Таким образом, уравнение луча, направленного из фокуса $y=frac{3}{4}x-frac{9}{4}.$
Далее, найдем точку пересечения найденной прямой с параболой:
$$left{begin{array}{lcl}y=frac{3}{4}x-frac{9}{4}\y^2=12xend{array}right.Rightarrowleft{begin{array}{lcl}3x-4y-9=0\x=frac{y^2}{12}end{array}right.Rightarrowleft{begin{array}{lcl}frac{3y^2}{12}-4y-9=0\x=frac{y^2}{12}end{array}right.Rightarrow$$ $$left{begin{array}{lcl}y^2-16y-36=0\x=frac{y^2}{12}end{array}right.$$
$$y^2-16y-36=0$$
$$D=256+4cdot1cdot36=256+144=400.$$
$$y_1=frac{16+20}{2}=18qquad y_2=frac{16-20}{2}=-2.$$
Поскольку по условию луч падает под острым углом, то мы рассматриваем только положительную координату $y=18.$ Соответствующее значение $x=frac{18^2}{12}=frac{324}{12}=27.$
Таким образом, луч пересекает параболу в точке $(27, 18).$
Далее найдем уравнение касательной к параболе в найденной точке $(27, 18)$ по формуле $(y-y_0)=y'(x_0)(x-x_0):$
$$y=sqrt{12x}Rightarrow y’=sqrt {12}frac{1}{2sqrt x}=frac{sqrt 3}{sqrt{x}}Rightarrow$$
$$Rightarrow y'(27)=frac{sqrt 3}{sqrt{ 27}}=frac{1}{3}.$$
$$y(27)=18.$$
Подставляем все найденные значения в уравнение касательной:
$y-18=frac{1}{3}(x-27)Rightarrow 3y-54=x-27Rightarrow x-3y+27=0.$
Далее, найдем угол $beta$ между лучем $y=frac{3}{4}x-frac{9}{4}$ и касательной $x-3y+27=0.$ Для этого оба уравнения запишем в виде $y=k_1x+b_1$ и $y=k_2+b_2$ угол вычислим по формуле $tg(L_1, L_2)=frac{k_1-k_2}{1+k_1cdot k_2}$
$$L_1: y=frac{3}{4}x-frac{9}{4}Rightarrow k_1=frac{3}{4};$$
$$L_2: x-3y+27=0Rightarrow y=frac{1}{3}x+9Rightarrow k_2=frac{1}{3}.$$
$$tg beta=tg(L_1, L_2)=frac{frac{3}{4}-frac{1}{3}}{1+frac{3}{4}frac{1}{3}}=frac{frac{5}{12}}{frac{5}{4}}=frac{1}{3}.$$
Легко увидеть, что угол между лучем $L_1,$ направленным из фокуса и его отражением равен $pi-2beta,$ а угол между отраженным лучем и осью $Ox$ $pi-(pi-2beta)-alpha=2beta-alpha.$
Зная $tgbeta=frac{1}{3}$ и $tgalpha=k_1=frac{3}{4}$ и вспоминая формулы для двойного угла тангенса и тангенс разности, находим $tg(2beta-alpha):$
$$tg 2beta=frac{2tgbeta}{1-tg^2beta}=frac{frac{2}{3}}{1-frac{1}{9}}=frac{frac{2}{3}}{frac{8}{9}}=frac{3}{4}.$$
$$tg(2beta-alpha)=frac{tg2beta-tgalpha}{1+tg2beta tgalpha}=frac{frac{3}{4}-frac{3}{4}}{1+frac{3}{4}frac{3}{4}}=0.$$ Следовательно, прямая, содержащая отраженный луч параллельна оси $Ox.$ Так как она проходит через точку $(27, 18),$ то можно записать ее уравнение $y=18.$
Ответ: $y=18.$