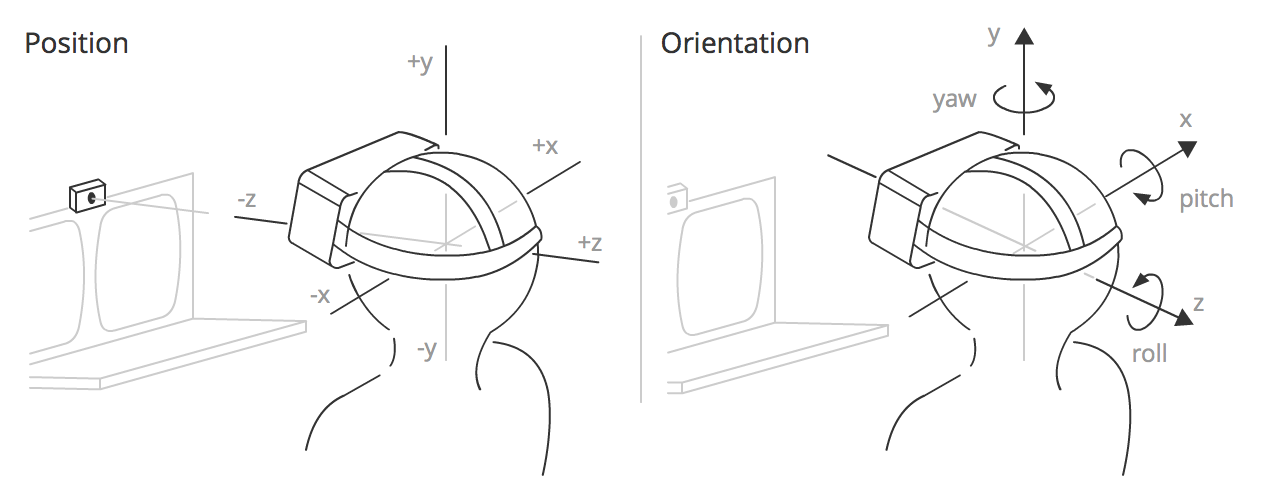
Отслеживание положения (positional tracking) представляет собой сочетание аппаратных средств и программного обеспечения, которое позволяет определить абсолютное положение объекта в пространстве. Данная технология является критически важной для достижения эффекта погружения в виртуальную реальность. В сочетании с отслеживанием ориентации становится возможным измерять и передавать в ВР все 6 степеней свободы (6-DoF) реального мира. В ходе работы с технологиями виртуальной реальности в нашей компании мы получили определенный опыт в данном вопросе и хотели бы им поделиться, рассказав про существующие способы отслеживания положения для виртуальной реальности, а также о плюсах и минусах того или иного решения.
Небольшая классификация
Совокупность методов и подходов к решению данной задачи можно поделить на несколько групп:
- Акустические
- Радиочастотные
- Магнитные
- Оптические
- Инерциальные
- Гибридные
Человеческое восприятие предъявляет высокие требования к точности (~1мм) и задержкам (< 20 мс) в ВР оборудовании. Оптические и инерционные методы наиболее близки к данным требованиям, и чаще всего используются совместно, дополняя друг друга. Рассмотрим базовые принципы, на которых построены вышеперечисленные методы.
Акустические методы
Акустические приборы слежения используют ультразвуковые (высокочастотные) звуковые волны для измерения положения и ориентации целевого объекта. Для определения положения объекта измеряется время пролёта (time-of-arrival) звуковой волны от передатчика к приёмникам, либо разность фаз синусоидальной звуковой волны при приёмо-передаче. Компания Intersense разрабатывает устройства отслеживания позиции на основе ультразвука.
Акустические трекеры, как правило, имеют низкую скорость обновления, вызванную низкой скоростью звука в воздухе. Другая проблема состоит в том, что скорость звука в воздухе зависит от таких факторов внешней среды, как температура, барометрическое давление и влажность.
Радиочастотные методы
Методов основанных на радиочастотах множество. Во многом по принципам определения положения они схожи с акустическими методами отслеживания (отличие лишь в природе волны). Наиболее перспективными на данный момент являются UWB (Ultra-Wide Band) методы, но даже в лучших решениях на основе UWB точность достигает только порядка сантиметров (DW1000 от DecaWave, Dart от Zebra Technologies, Series 7000 от Ubisense и другие). Возможно, в будущем стартапам вроде Pozyx или IndoTraq удастся достичь суб-миллиметровой точности. Однако пока UWB решения для отслеживания позиции не применимы для виртуальной реальности.
Другие методы позиционирования на радиочастотах более подробно описаны в данной статье.
Магнитные методы
Магнитный трекинг основан на измерении интенсивности магнитного поля в различных направлениях. Как правило, в таких системах есть базовая станция, которая генерирует переменное или постоянное магнитное поле. Так как сила магнитного поля уменьшается с увеличением расстояния между точкой измерения и базовой станцией, можно определить местоположение контроллера. Если точка измерения вращается, распределение магнитного поля изменяется по различным осям, что позволяет определить ориентацию. Наиболее известными продуктами на основе магнитного трекинга являются контроллер Razer Hydra и система STEM от компании Sixense.
Точность данного метода может быть достаточна высока в контролируемых условиях (в спецификациях Hydra говорится о 1 мм позиционной точности и 1 градусе точности ориентации), однако магнитное отслеживание подвержено помехам от токопроводящих материалов вблизи излучателя или датчика, от магнитных полей, создаваемых другими электронными устройствами и ферромагнитными материалами в пространстве отслеживания.
Оптические методы
Оптические методы представляют собой совокупность алгоритмов компьютерного зрения и отслеживающих устройств, в роли которых выступают камеры видимого или инфракрасного диапазона, стерео-камеры и камеры глубины.
В зависимости от выбора системы отсчёта выделяют два подхода для отслеживания положения:
- Outside-in подход подразумевает присутствие неподвижного внешнего наблюдателя (камера), определяющего положение движущегося объекта по характерным точкам. Используется в Oculus Rift (Constrellation), PSVR, OSVR и множестве Motion Capture систем.
- Inside-out подход предполагает наличие на движущемся объекте оптического сенсора, благодаря которому возможно отслеживать движение относительно неподвижных точек в окружающем пространстве. Используется в Microsoft Hololens, Project Tango (SLAM), SteamVR Lighthouse (гибридный вариант, т.к. есть базовые станции).
Также в зависимости от наличия специальных оптических маркеров выделяют отдельно:
- Безмаркерный трекинг как правило строится на сложных алгоритмах с использованием двух и более камер, либо стерео камер с сенсорами глубины.
- Трекинг с использованием маркеров предполагает заранее заданную модель объекта, которую можно отслеживать даже с одной камерой. Маркерами обычно служат источники инфракрасного излучения (как активные, так и пассивные), а также видимые маркеры наподобие QR-кодов. Такой вид трекинга возможен только в пределах прямой видимости маркера.
Задача Perspective-n-Point (PnP)
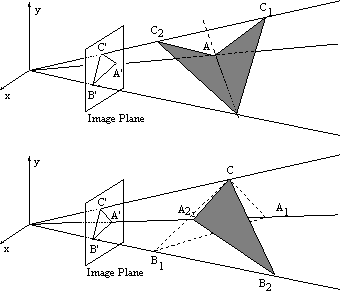
При оптическом отслеживании для определения положения объекта в пространстве решается так называемая задача PnP (Perspective-n-Point), когда по перспективной проекции объекта на плоскость сенсора камеры необходимо определить положение объекта в 3D-пространстве.
Для заданной 3D-модели объекта и 2D-проекции объекта на плоскость камеры решается система уравнений. В результате чего получается множество возможных решений. Количество решений зависит от числа точек в 3D-модели объекта. Однозначное решение для определения 6-DoF положения объекта можно получить как минимум при 4 точках. Для треугольника получается от 2 до 4 возможных решений, то есть положение не может быть определено однозначно:
Решение предлагается достаточно большим количеством алгоритмов, реализованных в виде библиотек:
- POSIT
- posest
- OpenCV (solvePnP)
SLAM — Simultaneous Localization and Mapping
Метод одновременной локализации и построения карты (SLAM) — это наиболее популярный способ позиционирования в робототехнике (и не только), который применяется для отслеживания положения в пространстве.
Алгоритм состоит из двух частей: первая — составление карты неизвестного окружающего пространства на основе измерений (данные с одометра или стерео-камеры), вторая — определение своего местоположения (локализация) в пространстве на основе сравнения текущих измерений с имеющейся картой пространства. Данный цикл непрерывно перевычисляется, при этом результаты одного процесса участвуют в вычислениях другого процесса. Наиболее популярные методы решения задачи включают в себя фильтр частиц и расширенный фильтр Калмана. На самом деле SLAM — это довольно обширная тема, а не только один определенный алгоритм, и разбор всех существующих решений на данную тему тянет на отдельную статью.
SLAM удобен для мобильных решений виртуальной и дополненной реальности. Однако недостатком данного подхода является большая вычислительная сложность, что в купе с требовательными VR/AR приложениями будет сильно загружать производительные ресурсы аппарата.
Project Tango от Google и Microsoft Hololens являются наиболее известными проектами на основе SLAM для мобильных устройств. Также ожидается поддержка трекинга на основе SLAM в недавно анонсированных продуктах от Intel (Project Alloy) и Qualcomm (VR820).
Среди open-source решений можно выделить ORB-SLAM, LSD-SLAM, PTAM-GPL.
Инерциальный трекинг
Современные инерциальные измерительные системы (IMU) на основе MEMS-технологии позволяют отслеживать ориентацию (roll, pitch, yaw) в пространстве с большой точностью и минимальными задержками.
Благодаря алгоритмам «sensor fusion» на основе комплементарного фильтра или фильтра Калмана данные с гироскопа и акселерометра успешно корректируют друг друга и обеспечивают точность как для кратковременных измерений, так и для длительного периода.
Однако определение координат (перемещения) за счёт двойного интегрирования линейного ускорения (dead reckoning), вычисленного из сырых данных с акселерометра, не удовлетворяет требованиям по точности на длительных периодах времени. Акселерометр сам по себе даёт сильно зашумленные данные, и при интегрировании ошибка увеличивается со временем квадратично.
Решить данную проблему помогает комбинирование инерциального подхода к трекингу с другими методами, которые периодически корректируют, так называемый, дрифт акселерометра.
Гибридные методы
Так как ни один из методов не является безупречным, и все они имеют свои слабые места, наиболее разумно комбинировать различные методы отслеживания. Так инерциальный трекинг (IMU) может обеспечить высокую частоту обновления данных (до 1000 Гц), в то время как оптические методы могут дать стабильную точность в длительные периоды времени (корректирование дрифта).
Гибридные методы отслеживания основаны на алгоритмах «Sensor Fusion», наиболее популярным из которых является расширенный фильтр Калмана (EKF — Extended Kalman Filter).
Как работает SteamVR Lighthouse?
Система трекинга HTC Vive состоит из двух базовых станций, оптических сенсоров и инерциальных измерительных блоков (IMU) в контроллерах и шлеме. Базовые станции состоят из двух вращающихся лазеров и массива инфракрасных светодиодов. Один из лазеров вращается вертикально, второй — горизонтально. Таким образом лазеры по очереди «сканируют» окружающее пространство. Базовые станции работают синхронно: в определенный момент времени только один из четырёх лазеров «сканирует» пространство трекинга. Для синхронизации работы всей системы между каждыми включением лазеров всё окружающее пространство освещается инфракрасным световым импульсом.
Сенсоры на контроллерах и шлеме фиксируют все оптические импульсы с базовых станций и измеряют время между ними. Так как частота вращения лазеров заранее известна (60 Гц), по времени между импульсами можно вычислить углы поворота каждого из лучей. Что даёт нам 2D-координаты оптического сенсора, зная взаимное расположение сенсоров на контроллере можно легко восстановить 3D-положение контроллера в пространстве (задача PnP). При одновременной видимости двух базовых станций 3D-положение контроллера может быть вычислено из пересечения двух лучей, что даёт более точные результаты и при этом требует меньше вычислений. Более наглядно процесс трекинга продемонстрирован ниже.
Месяц назад компания Valve объявила о том, что открывает свою систему трекинга для сторонних разработчиков. Более подробно об этом можно прочитать здесь.
Какой из методов отслеживания позиции в пространстве наиболее перспективен для виртуальной/дополненной реальности по вашему мнению?
Это первая статья из цикла про технологи ВР, если будет интерес, то мы продолжим писать их и дальше.
P.S. Почему нет хаба виртуальная реальность?
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Интересны ли Вам материалы затрагивающие технические подробности при создании технологий виртуальной реальности?
4.35%
нет, эта тема нам не интересна
4
Проголосовали 92 пользователя.
Воздержались 6 пользователей.
В PowerPoint есть довольно много инструментов для создания визуально интересной презентации. Вы можете создавать в нем всевозможные диаграммы и графики, и вы даже можете связать его с листом Excel при построении диаграммы. Отчасти он особенно хорош тем, что вставляемые фигуры можно связывать и группировать вместе, чтобы их было легче выровнять. Помимо группировки и направляющих выравнивания / привязки, вы также можете скопировать точное положение объектов и применить его к другим объектам, чтобы упростить выравнивание. Вот как.
Положение объектов
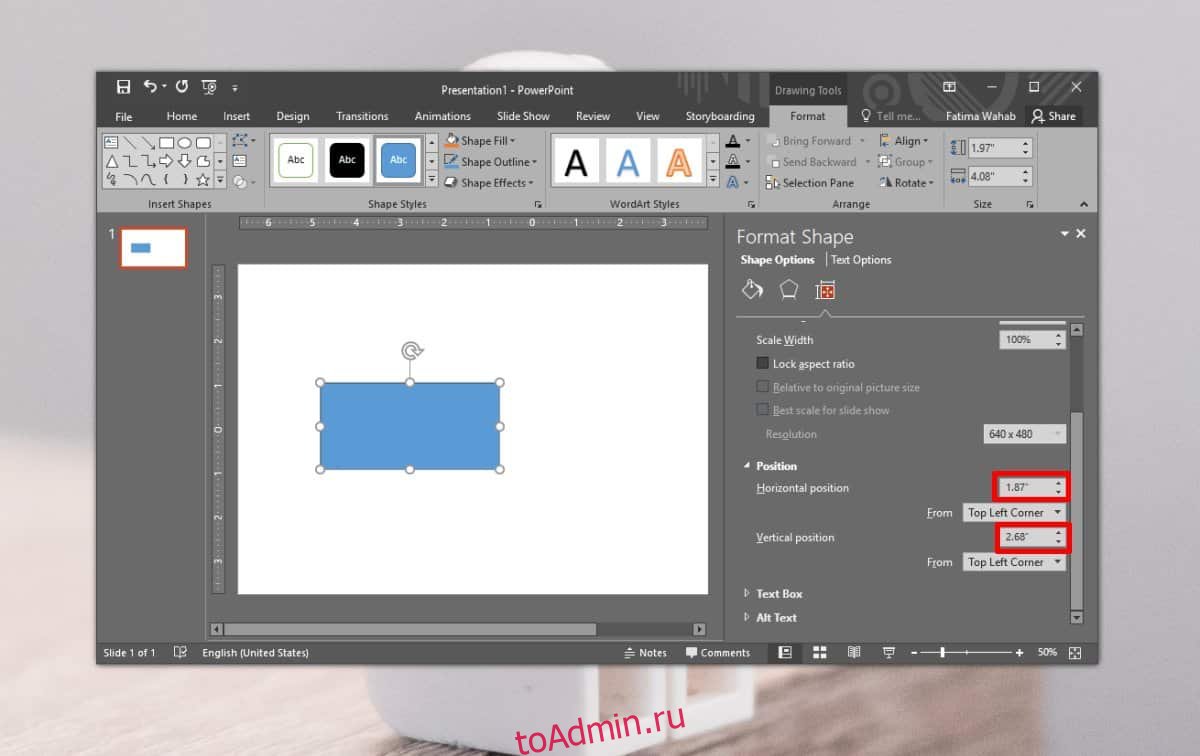
Откройте PowerPoint и вставьте любой объект. Мы возьмем простой заполненный прямоугольник и разместим его где-нибудь на пустом слайде. Вы можете использовать любую форму или другой объект, который захотите. Щелкните его правой кнопкой мыши и выберите в меню «Размер и положение».
Это откроет панель свойств справа с выделенным разделом для позиции. Положение указывается в сантиметрах, поскольку это единица измерения по умолчанию, которую использует линейка в PowerPoint (и во всех других приложениях Microsoft Office). На скриншоте ниже синий прямоугольник расположен на 1,87 ″ на горизонтальной линейке или оси x и на 2,68 ″ на вертикальной линейке или оси y.
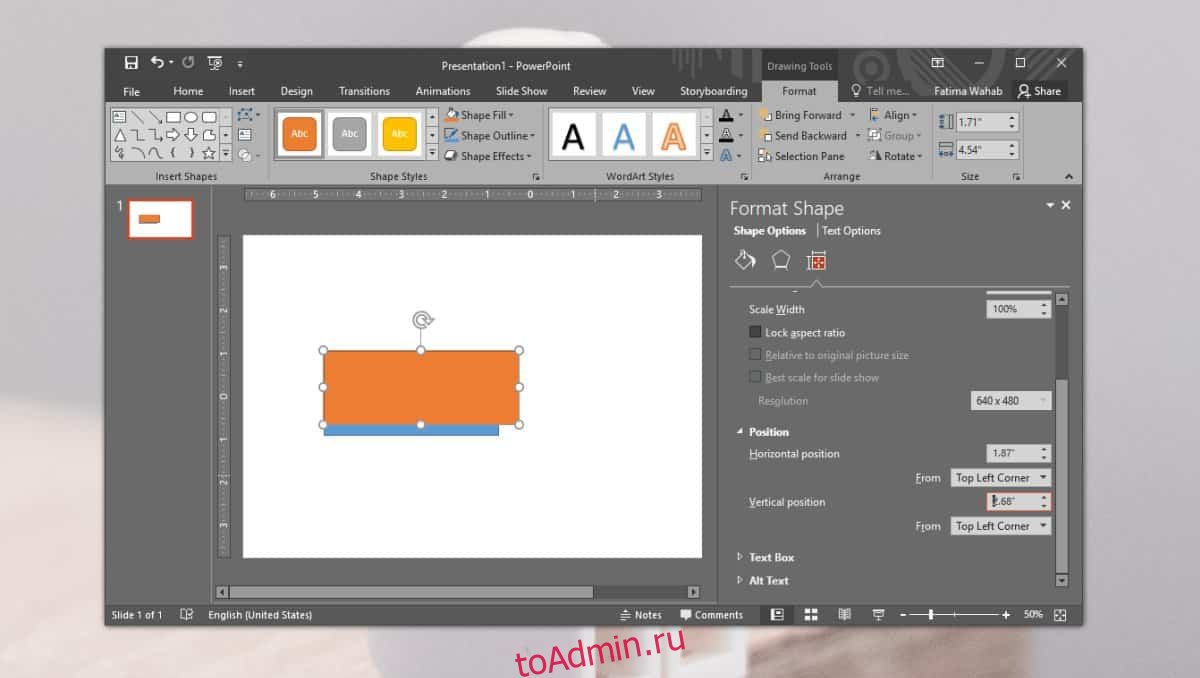
Чтобы скопировать это точное положение и применить его к другому объекту, вам нужно сначала записать значения. Затем вставьте второй объект. Я добавляю еще один прямоугольник, но он не того же размера, что и первый.
Щелкните объект правой кнопкой мыши и выберите в меню «Размер и положение». Объект будет иметь свои собственные координаты положения в зависимости от того, где вы его установили. Щелкните внутри поля Горизонтальное положение и введите положение, в которое вы хотите его переместить. Коснитесь Enter. Повторите это для вертикального положения, и элемент будет идеально совмещен с предыдущим.
Два объекта, которые я выстроил в линию, имеют разный размер, и когда вы выровняете их, вы увидите, что объекты «начинаются» из верхнего левого угла, т.е. из верхнего левого угла прямоугольника. Вот что определяет его позицию.
С прямоугольниками выстраивать элементы легко, но если у вас есть форма или объект, у которого нет прямой линии для края, например, круга, это может быть лучшим способом выровнять их.
В PowerPoint есть направляющие, но иногда из-за размера объекта направляющие не всегда идеально выстраивают элементы. Если вы выстроили предметы в ряд, но они вам не подходят, вы можете проверить их положение, чтобы определить, правильно они выстроены или нет.
В Photoshop есть похожая функция, хотя его руководства намного умнее, чем в PowerPoint.
Что вы думаете об этой статье?
Свойства тонкой линзы определяются главным образом расположением ее главных фокусов. Поэтому, зная расстояние от источника света до линзы, а также ее фокусное расстояние (положение фокусов), мы можем определить расстояние до изображения, опустив описание хода лучей внутри самой линзы. Поэтому в изображении на чертеже точного вида сферических поверхностей линзы необходимость отсутствует.
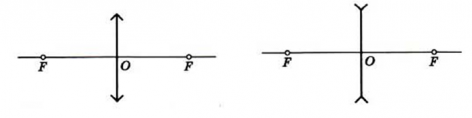
Схематически тонкие линзы обозначают отрезком со стрелками на конце. Они смотрят от центра в противоположные стороны, если линза собирающая, и они направлены к центру отрезка, если линза рассеивающая.
Внимание!
Напомним, что линзы могут давать действительные и мнительные изображения. Причем, собирающая линза может давать как действительные, так и мнимые изображения. Рассеивающая линза всегда дает только мнимые изображения.
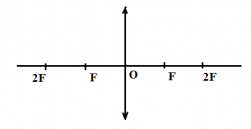
Способ построения изображений, а также вид самих изображений в линзе зависит от того, где расположен изображаемый предмет. Он может располагаться за двойным фокусным расстоянием, в фокальной плоскости второго фокуса, между вторым и первым фокусом, в фокальной плоскости главного фокуса и на расстоянии меньше фокусного расстояния линзы.
Определение
Вторым фокусом называют точку, которая расположена на главной оптической оси от главного фокуса на расстоянии, равном фокусному расстоянию линзы. Относительно линзы он располагается на расстоянии, равном двойному фокусному расстоянию линзы.
Построение изображения в собирающей линзе
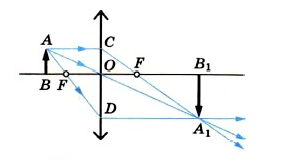
Предметы схематично изображаются в виде стрелки. Чтобы построить изображение предмета в собирающей линзе, нужно найти положение верхней и нижней точки этого изображения. Сначала находят положение точки изображения, соответствующей верхней точки предмета (точки А). Для этого из этой точки нужно пустить два луча:
Два вида лучей при построении изображений в линзе
Первый луч проходит из верхней точки предмета (точки А) параллельно главной оптической оси. На линзе (в точке С) луч преломляется и проходит через точку фокуса (точку F).
Второй луч необходимо направить из верхней точки предмета (точки А) через оптический центр линзы (точку О). Он пройдет, не преломившись.
На пересечении двух лучей обозначаем точку А1. Это и будет изображение верхней точки предмета. Таким же образом нужно поступить с нижней точкой предмета. Но на пересечении вышедших из линзы лучей нужно поставить точку В1. Изображение предмета при этом — А1 В1.
В зависимости от того, где расположен предмет, изображение может получиться действительным или мнимым, увеличенным или уменьшенным, перевернутым или прямым. Построим изображения для каждого из таких случаев.
| Схема построения изображения | Расположение предмета относительно линзы + характеристика изображение |
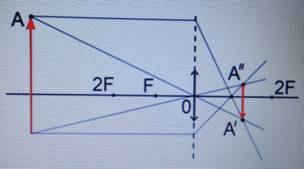 |
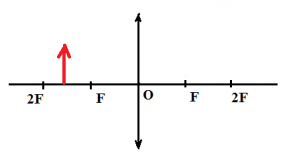
Предмет располагается за двойным фокусом.
Изображение:
|
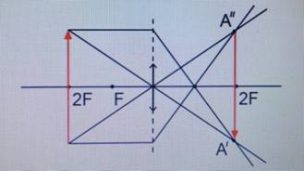 |
Предмет располагается в фокальной плоскости второго фокуса.
Изображение:
|
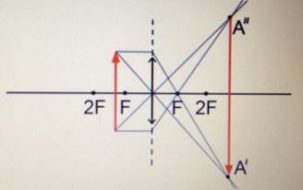 |
Предмет располагается в пространстве между фокусом и двойным фокусом.
Изображение:
|
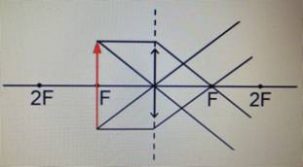 |
Предмет находится в фокальной плоскости.
Изображения нет, поскольку лучи идут параллельно друг другу и не пересекаются. |
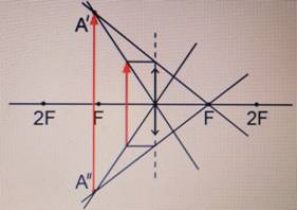 |
Предмет располагается между линзой и фокусом.
Изображение:
|
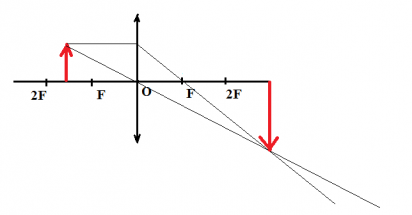
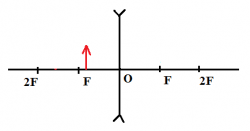
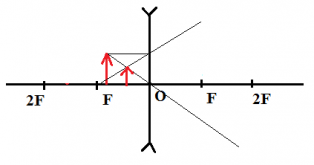
Пример №1. Построить изображение предмета, изображенного на рисунке. Определить тип изображения.
Чтобы построить изображение предмета, достаточно определить его положение одной точки — верхней. Поскольку предмет расположен параллельно линзе, для построения изображения, достаточно будет соединить найденную точку изображения для верхней точки предмета перпендикуляром, проведенным к главной оптической оси.
Чтобы построить изображение верхней точки, пустим от нее два луча — побочную оптическую ось через оптический центр и перпендикуляр к линзе. Затем найдем пересечение побочной оптической оси с преломленным лучом. Теперь пустим перпендикуляр к главной оптической оси и получим изображение. Оно является действительным, увеличенным и перевернутым.
Частный случай — построение изображения точки
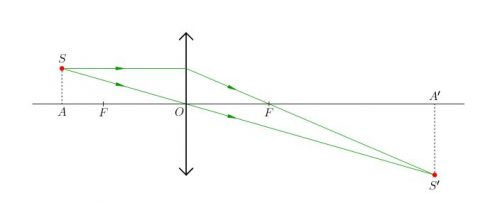
Положение изображения точки можно найти тем же способом, описанным выше. Нужно лишь построить два луча и найти их пересечение после выхода из линзы (см. рисунок ниже). Так, изображению точки S соответствует точка S´.
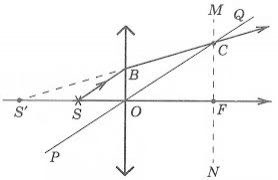
Особую сложность составляет случай, когда точка расположена на главной оптической оси. Сложность заключается в том, что все лучи, которые можно построить, будут совпадать с главной оптической осью. Поэтому возникает необходимость в определении хода произвольного луча. Направим луч от точки S (луч SB) к собирающей линзе. Затем построим побочную оптическую ось PQ такую, которая будет параллельна лучу SB. После этого построим фокальную плоскость и найдем точку пересечения (точка С) фокальной плоскости с побочной оптической осью. Теперь соединим полученную точку С с точкой В. Это будет преломленный луч. Продолжим его до пересечения с главной оптической осью. Точка пересечения с ней и будет изображением точки S. В данном случае оно является мнимым.
Пример №2. Построить изображение точки, расположенной на главной оптической оси.
Чтобы построить изображение, пустим произвольный луч к линзе. Затем построим параллельную ему побочную оптическую ось и фокальную плоскость. Из места пересечения этой оси с фокальной плоскостью пустим луч, также проходящий через точку пересечения линзы с произвольным лучом. Построим продолжение луча до получения точки пересечения с главной оптической осью. Отметим точку пересечения — она является действительным изображением точки.
Построение изображения в рассеивающей линзе
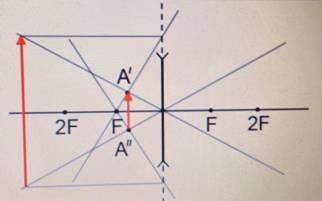
Чтобы построить изображение предмета в рассеивающей линзе, нужно определить положения точек изображения, соответствующих верхней и нижней точкам предмета. Вот как определить положение точки изображения для верхней точки предмета:
- Нужно пустить луч, перпендикулярный главной оптической оси. Этот луч после преломления отклонится. Но его продолжение обязательно пересечет главный фокус линзы.
- Нужно пустить луч от верхней точки предмета через оптический центр линзы (построить побочную оптическую ось).
- Точку пересечения продолжения луча, полученного в шаге 1, с побочной оптической осью, нужно обозначить за изображение верхней точки предмета (на рисунке это точка А´).
Точно такие же действия нужно выполнить для нижней точки предмета. В результате получится точка пересечения, соответствующая изображению нижней точки предмета (на рисунке это точка А´´).
Внимание! Независимо от расположения предмета относительно рассеивающей линзы, изображение всегда получается прямым, уменьшенным, мнимым.
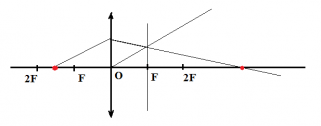
Пример №3. Построить изображение предмета в рассеивающей линзе.
Чтобы построить изображение, пустим от верхней точки предмета побочную оптическую ось через оптический центр и проведем перпендикуляр к линзе. Затем из точки главного фокуса проведем луч через точку пересечения линзы с перпендикуляром. Пересечение этого луча с побочной оптической осью есть изображение верхней точки предмета. Теперь проведем от нее перпендикуляр к главной оптической оси. Это и будет являться изображением предмета. Оно является мнимым, уменьшенным и прямым.
Построение изображений в плоском зеркале
Определение
Плоское зеркало — это плоская поверхность, зеркально отражающая свет.
Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света. Продемонстрируем это с помощью рисунка ниже.
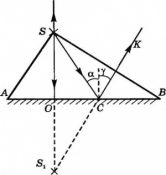
Построим изображение точечного источника S. От точечного источника света лучи распространяются во все стороны. На зеркало падает пучок света ASB, и изображение создается всем пучком сразу. Но для построения изображения достаточно взять любые два луча из этого пучка. Пусть это будут лучи SO и SC. Луч SO падает перпендикулярно поверхности зеркала АВ. Поскольку угол между ним и перпендикуляром, восстановленным в точке падения, равен 0, то угол падения принимаем равным за 0. поэтому отраженный пойдет в обратном направлении OS. Луч SC отразится под углом γ=α. Отраженные лучи OS и СК расходятся и не пересекаются, но если они попадают в глаз человека, то человек увидит изображение S1, которое представляет собой точку пересечения продолжения отраженных лучей.
Таким образом, чтобы получить изображение в плоском зеркале, нужно:
- Пустить от источника света луч, перпендикулярный к плоскости зеркала (падающий луч совпадает с отраженным лучом).
- Пустить от источника света к плоскости зеркала еще один луч под произвольным углом.
- Построить отраженный луч от падающего луча, построенного в шаге 2, используя закон отражения света.
- Найти пересечение продолжений отраженных от зеркала лучей (пущенного под прямым углом и произвольным углом).
Внимание!
Изображение в зеркале всегда является мнимым. Это связано с тем, что изображение строится на пересечении продолжении лучей, а не на самих лучах.
Изображение в плоском зеркале находится от зеркала на таком же расстоянии, как предмет от этого зеркала. Это легко доказать тем, что треугольники SOC и S1OC равны по стороне и двум углам. Следовательно SO = S1O. Отсюда делаем вывод, что для построения изображения точечного источника света достаточно знать расстояние, на котором он находится от зеркала. Останется только провести к зеркалу перпендикулярную прямую и отложить на ней точку на нужном расстоянии.
При построении изображения какого-либо предмета последний представляют как совокупность точечных источников света. Поэтому достаточно найти изображение крайних точек предмета. Так, изображение А1В1 соответствует предмету АВ.
Изображение и сам предмет всегда симметричны относительно зеркала.
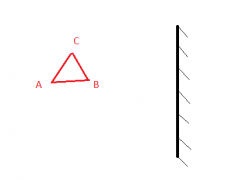
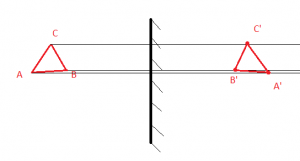
Пример №4. Построить изображение треугольника ABC в плоском зеркале.
Чтобы построить изображение, пустим к плоскому зеркалу перпендикулярные прямые. Затем измерим расстояние от каждой точки до зеркала и отложим их по перпендикуляру от зеркала в обратную сторону. Так для точки А мы находим точку А´, для В — В´, для С — С´.
Видно, что треугольник отразился зеркально (изображение и предмет симметричны друг другу). Так и должно быть в случае с зеркалом.
Задание EF17760

Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Сделать рисунок — построить изображение в линзе.
3.Записать формулу для нахождения площади полученной фигуры.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Оптическая сила линзы: D = 2,5 дптр.
• Сторона треугольника AC = 4 см.
4 см = 0,04 м
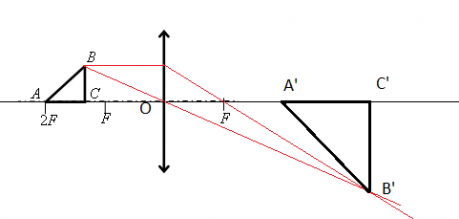
Построим изображение в линзе. Для этого достаточно построить изображение точки В. Сначала пустим луч, параллельный главной оптической оси, к плоскости линзы. Он будет преломляться, после чего пройдет через фокус. Затем пустим луч через оптический центр. На месте пересечения двух лучей поставим точку и обозначим ее за B´.
Так как точки B и C предмета лежат на одной прямой, перпендикулярной главной оптической оси, для нахождения точки изображения C´ достаточно пустить перпендикуляр от B´ этой оси. На месте пересечения поставим точку и обозначим ее C´.
Рассматривать ход лучей для построения точки A´ тоже не будем. Точка A лежит в плоскости второго фокуса. Значит, она будет находиться в этой же точке и с противоположной стороны линзы. Это легко доказать с помощью формулы тонкой линзы:
1d+1f=1F
Если расстояние от предмета до линзы равно 2F, то и расстояние от линзы до его изображения будет 2F:
12F+1f=1F
1f=1F−12F=2−12F=12F
f=2F
Теперь соединим все найденные точки и получим треугольник A´ B´ C´. Найдем его площадь. Поскольку это прямоугольный треугольник, его площадь будет равна половине произведения двух катетов — B´ C´и A´ C´:
S=A´C´·B´C´2
Из формулы оптической силы линзы найдем фокусное расстояние:
F=1D=12,5=0,4 (м)
Известно, что точка A находится в точке двойного фокусного расстояния. И ее изображение тоже находится на таком же расстоянии от линзы. Следовательно, чтобы найти длину катета A´ C´, нужно найти расстояние от точки C до ее изображения. Расстояние от этой точки до линзы равно разности двойного фокусного расстояния и длины отрезка AC:
dC=2F−AC=2·0,4−0,04=0,76 (м)
Используя формулу тонкой линзы, вычислим расстояние от линзы до изображения этой точки:
10,76+1f=1F
1fC=1F−10,76=0,76−F0,76F=0,76−0,40,76·0,4
fC=0,76·0,40,76−0,4=0,844 (м)
Тогда длина катета A´ C´ будет равна:
A´C´=fC−fA=fC−2F=0,844−0,4·2=0,044 (м)
Треугольники BCO и B´ C´O подобны по 3 углам. Углы O равны как вертикальные. Углы C и C´ как прямые, а B и B´ как накрест лежащие (полученные при пересечении секущей в виде луча через оптический центр и параллельных фокальных плоскостей). Следовательно BC относится к B´ C´ так же, как OC относится к C´O:
BCB´C´=ACA´C´
Треугольник ABC равнобедренный, поэтому BC = AС. Тогда:
ACB´C´=ACA´C´
Следовательно:
B´C´=A´C´
Отсюда площадь треугольника равна:
S=A´C´·A´C´2=(0,044)22=0,000968 (м2)=9,68 (см2)
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18181
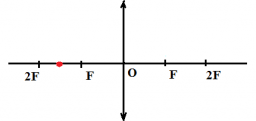
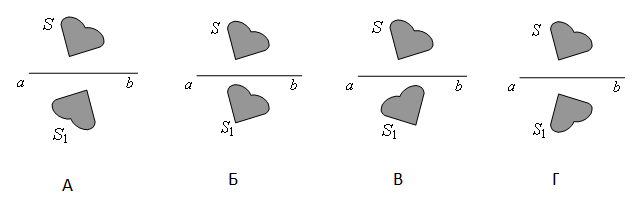
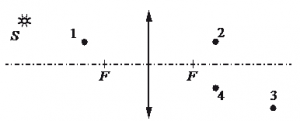
Предмет S отражается в плоском зеркале ab. На каком рисунке верно показано изображение S1 этого предмета?
Ответ:
Алгоритм решения
- Записать, какое изображение дает плоское зеркало.
- Выбрать изображение, которое соответствует типу описанного изображения.
Решение
Зеркало дает мнимое изображение предмета без увеличения в зеркальном отражении. Это значит, что предмет и его изображение должны быть симметричны относительно плоскости зеркала. Симметричными являются только предмет и его изображение на последнем рисунке — Г.
Ответ: Г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18876
Алгоритм решения
1.Построить изображение точки.
Решение
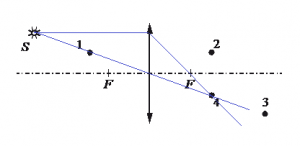
Построим изображение точки с учетом того, что линза собирающая. Для этого пустим из этой точки луч света, параллельный главной оптической оси. После прохождения через линзу луч преломится и пройдет через фокус. Затем пустим луч от этой точки через оптический центр линзы. Точка, в которой оба луча пересекутся, будет искомой. В данном случае это точка 4.
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 32.4k
Тема:
«Определение
месторасположения предметов в пространстве: близко, далеко, вверху, вниз.»
Цель:
1.
Образовательная: формировать пространственные понятия: далеко- близко, дальше-
ближе, к, от; учить ориентироваться в пространстве, использовать изученные
понятия в речи.
2.
Коррекционно-развивающая: развивать мышление, произвольное внимание.
3.
Воспитательная: воспитывать интерес к учению, умение слушать друг друга, культуру
поведения на уроке.
Ход
урока
Здравствуйте,
ребята. Посмотрите, чтобы у вас на партах было все приготовлено.
Самомассаж
и позитивный эмоциональный настрой на работу:
—
С помощью массажа настроимся на работу.
—
Соедините ладони вместе и потрите их друг о друга (10 сек).
—Вы готовы глазки?
(поглаживание век)
-Вы
готовы ушки? (растирание мочек ушек)
-Вы
готовы ручки? (поглаживание)
-Вы
готовы? (развести руки в стороны и обнять себя)
-Улыбнулись
друг другу и гостье. Я желаю вам успеха.
Дыхательное
упражнение:
«Варим
кашу» После сделанного глубокого вдоха, на каждом выдохе произносить слово пых
и так 8 раз.
Изучение
нового материала
Игра,
подготавливающая к сообщению темы и задач урока:
-На
доске символы.
Предмет
в /внутри
на/сверху
около/близко, рядом
под/внизу.
-У
вас на партах картинки животных, возьмите их в руки и покажите мне действия:
—
Смотрите на символы, показываете действие и проговариваете его друг за другом —
«цепочкой».
Кот
на парте;
кот
под парту;
кот в портфеле;
кот
около парты;
возьмите
картинку в правую руку, положите на парту справа;
возьмите
картинку в левую руку, положите на парту слева;
картинка—-на
середину парты;
поднимите
картинку вверх, опустите вниз.
-Ребята,
какие слова мы употребляли сейчас?
—
Это слова-помощники помогают понять, как именно нужно перемещать предмет в
пространстве или перемещаться самому. Вот мы и подошли к теме сегодняшнего
урока.
Сообщение
темы и целей:
—
Сегодня на уроке будем тренироваться определять положение предметов в
пространстве и вместе с тем правильно учиться говорить, выражать свои мысли.
-А
сейчас мне понадобятся помощники.
1.
Встань …(имя ребенка) близко к доске.
2.
Встань … (имя ребенка) далеко от…(имя ребенка).
3.
Встань (имя ребенка) ближе к (имя ребенка).
4.
Встань (имя ребенка) дальше от …(имя ребенка).
5.
Встань (имя ребенка) ближе к ….,и дальше от…
6.
Встать близко ко- мне
Давайте
обнимемся и пожелаем удачи друг другу.
Зрительная
гимнастика
1.
Плотно закрыть и широко открыть глаза. (3 раза).
2.
Посмотреть вверх, вниз, вправо, влево, не поворачивая головы..
3.
Вращение глазами по кругу. (3 раза под счёт в одну и в другую сторону).
4.
Посмотреть на кончик пальца (30 см от глаз), затем вдаль. (5 раз).
Игра
«Верно – не верно»
Правила
игры. Ведущий называет признак весны и кидает мяч ребенку. Ребенок, получивший
мяч должен ответить «Верно», «Не верно».
Солнце
светит ярко и греет сильно
Снег
падает большими хлопьями
Дети
надевают шубы, шапки, валенки
Медведь
вышел из берлоги
Дети
ходят в валенках по лужам
В
небе летают ласточки
Дети
убирают территория школы
На
деревьях лежат шапки снега
На
деревьях распускаются почки
Дни
короткие, солнце светит мало
—
Молодцы.
Ребята
у вас на партах лежат геометрические фигуры
Расположите
их так, чтобы:
1.
Круг лежал близко к квадрату.
2.
Квадрат лежал близко к треугольнику.
3.
Треугольник лежал дальше от квадрата, но ближе к кругу.
4.
Треугольник лежал далеко от квадрата и круга.
5.
Круг лежал далеко от треугольника, но близко к квадрату.
6.
Круг лежит под квадратом, а треугольник на квадрате
Физминутка
(аудиозапись-
«Солнышко лучистое»)
Игра
«Далеко -близко»
—Нарисуй кружок рядом с
дверью
—
Нарисуй квадратик дальше от домика
—
Нарисуй треугольник над домом
—
Нарисуй цветочек в доме
—
Нарисуй прямоугольник справа от дома
-Нарисуй
овал слева от дома
-Молодцы!!
Ориентировка
на собственном теле.
-А
сейчас давайте проверим , как вы ориентируетесь с собственным телом.
-Давайте
вспомним, где у нас правая рука. Левая нога! Молодцы!
А
сейчас будут задания посложнее, вы готовы?
Дотронуться:
1.
Левой рукой до правой ноги
2.
Правой рукой до правого колена
3.
Левой рукой до левого плеча
4.
Правой рукой до левого локтя
5.
Левой рукой до правого уха
6.
Правой рукой до левого уха
7.
Правой рукой до носа.
8..Правой
рукой до правого локтя.
Молодцы
ребята! Я вижу, как вы стараетесь.
V.
Итог занятия
—
Чем мы занимались сегодня?
-Что
вы запомнили из сегодняшнего урока?
-Что
вам понравилось особенно?
VI.
Рефлексия.
—Какое у вас стало
настроение? Покажите
Анализировать движение может быть непросто. Но знание точных определений поможет нам в этом вопросе.
Что означает термин «положение»?
В физике мы просто обожаем точные описания движения объекта. Серьезно, первые несколько глав практически каждого учебника по физике посвящены объяснениям того, как точно описывать движение, поскольку это чрезвычайно важно для всего, что мы делаем в физике.
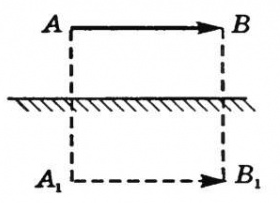
Для того чтобы описать движение объекта, мы должны научиться описывать его положение — где он находится в каждый конкретный момент времени. Точнее, мы должны определить его положение относительно определённой системы отсчёта. В качестве такой системы отсчёта, как правило, используется Земля, и мы чаще всего описываем положение предмета относительно других неподвижных предметов в данной системе отсчёта. Например, положение учительницы можно описать, объяснив, где она находится по отношению к классной доске (рисунок 1). В некоторых случаях мы можем использовать системы отсчета, которые не являются стационарными, а находятся в движении относительно Земли. Например, для описания положения пассажира в самолёте удобнее взять в качестве системы отсчёта не Землю, а самолёт (рисунок 2).
Переменная x, как правило, используется для указания горизонтального положения, а переменная y — для вертикального.
Что означает термин «перемещение»?
Если объект перемещается относительно системы отсчета, например, если учительница идёт вправо относительно доски или пассажир пошёл в хвост самолёта, тогда мы говорим, что изменилось положение объекта. Изменение положения называется перемещением. Термин перемещение подразумевает, что объект переместился или был перемещен.
Перемещение понимают, как изменение положения объекта. Его также можно определить при помощи следующей математической формулы:
start text, П, е, р, е, м, е, щ, е, н, и, е, end text, equals, delta, x, equals, x, start subscript, к, end subscript, minus, x, start subscript, 0, end subscript
x, start subscript, к, end subscript обозначает конечное положение объекта.
x, start subscript, 0, end subscript обозначает начальное положение.
delta, x символ, используемый для обозначения перемещения.
Перемещение — это векторная величина. Это значит, что у него есть величина и направление. Обозначается оно стрелкой, указывающей в направлении от начального до конечного положения. Например, на рисунке 1 показано перемещение учительницы относительно классной доски.
Рисунок 1. Учительница во время урока ходит влево и вправо. Перемещение учительницы на plus, 2, comma, 0, start text, м, end text относительно доски представлено стрелкой, указывающей вправо. (Изображение предоставлено Openstax College Physics)
Начальное положение учительницы — x, start subscript, 0, end subscript, equals, 1, comma, 5, start text, м, end text, а конечное положение составляет x, start subscript, к, end subscript, equals, 3, comma, 5, start text, м, end text. Таким образом, её перемещение может быть найдено следующим образом:,
delta, x, equals, x, start subscript, к, end subscript, −, x, start subscript, 0, end subscript, equals, 3, comma, 5, start text, space, м, end text, −, 1, comma, 5, start text, space, м, end text, equals, plus, 2, comma, 0, start text, space, м, end text.
В этой системе координат движение вправо имеет положительный знак, тогда как движение влево отрицательно.
Теперь рассмотрим пассажира, который ходит относительно координатной системы, связанной с самолётом. Рисунке 2.
Рисунок 2. Пассажир проходит от своего места в хвост самолёта. Перемещение пассажира на −, 4, comma, 0, start text, м, end text относительно самолёта обозначено стрелкой, направленной в сторону хвостовой части самолёта. (Изображение предоставлено Openstax College Physics)
Начальное положение пассажира самолета x, start subscript, 0, end subscript, equals, 6, comma, 0, start text, space, м, end text, а его конечное положение x, start subscript, к, end subscript, equals, 2, comma, 0, start text, space, м, end text, поэтому его перемещение находится по формуле: delta, x, equals, x, start subscript, к, end subscript, −, x, start subscript, 0, end subscript, equals, 2, comma, 0, start text, space, м, end text, −, 6, comma, 0, start text, space, м, end text, equals, minus, 4, comma, 0, start text, space, м, end text.
Перемещение получилось отрицательным, поскольку пассажир шёл в хвостовую часть самолёта, то есть в отрицательном направлении оси х в нашей системе координат.
Перемещение при прямолинейном движении может быть положительным и отрицательным. Приступая к решению задачи, сначала определитесь, какое направление считать положительным, обычно это вправо или вверх, но вы можете выбрать любое, какое вам удобно.
Что такое расстояние и пройденное расстояние?
В физике термин «расстояние» используется в двух случаях, поэтому нужно осторожно его использовать. Мы можем говорить о расстоянии между двумя точками или о расстоянии, пройденном объектом.
Расстояние определяется как величина перемещения между двумя точками. Обратите внимание, что расстояние между двумя точками и пройденное расстояние — разные вещи.
Пройденное же расстояние — это общая длина пути, преодолённого
объектом при движении из одной точки в другую. Пройденное расстояние не является вектором. У него нет направления, а следовательно, оно не может быть отрицательным. Например, учительница прошла расстояние 2, comma, 0, start text, space, м, end text, а пассажир самолёта — 4, comma, 0, start text, space, м, end text.
Важно отметить, что пройденное расстояние не всегда равно модулю перемещения (то есть расстоянию между двумя точками). В частности, если объект во время движения меняет направление, общее пройденное расстояние будет больше модуля перемещения между этими двумя точками. Ниже вы увидите примеры решения задач на эту тему.
Чем перемещение может сбить с толку?
Ученики часто забывают, что пройденное расстояние может быть больше модуля вектора перемещения. Под величиной или модулем мы понимаем длину вектора перемещения без учета его направления, то есть просто число и единицу измерения. Например, учительница могла несколько раз во время урока пройти туда-сюда перед доской, возможно, пройдя в общей сложности 150 метров, но в итоге оказаться всего в двух метрах справа от своей отправной точки. В этом случае ее перемещение будет равно plus, 2, start text, м, end text, величина или модуль ее перемещения будет составлять 2, start text, м, end text, а пройденное расстояние — 150, start text, м, end text. В кинематике чаще всего приходится иметь дело с перемещением и модулем перемещения, а пройденное расстояние встречается довольно редко. Представьте, что вы отметили начальное и конечное положение некоего объекта. Перемещение — это разница между этими точками, она не зависит от того, каким путём объект попал из первой точки во вторую. Пройденное же расстояние — это общая длина пути, пройденного объектом, пока он двигался от одной точки в другую.
Многие ученики, решая задачи на перемещение, часто забывают о минусе. Это иногда случается из-за того, что они случайно вычитают конечное положение из начального вместо того, чтобы вычесть начальное из конечного.
Как выглядят решение задач на нахождение перемещения?
Пример 1: Перемещение четырёх движущихся объектов
Четыре объекта движутся в соответствии с направлениями, показанными на диаграмме ниже. Предположим, что единицы измерения горизонтальной шкалы даны в метрах. (Изображение предоставлено: с Openstax College Physics, отредактировано)
Чему равно перемещение каждого объекта?
Начальное положение объекта А было 0, start text, space, м, end text, а конечное — 7, start text, space, м, end text. Перемещение объекта A находится по следующей формуле:
delta, x, start subscript, A, end subscript, equals, 7, start text, space, м, end text, minus, 0, start text, space, м, end text, equals, plus, 7, start text, space, м, end text
Начальное положение объекта B было 12, start text, space, м, end text, а конечное — 7, start text, space, м, end text. Перемещение объекта B находится по следующей формуле:
delta, x, start subscript, B, end subscript, equals, 7, start text, space, м, end text, minus, 12, start text, space, м, end text, equals, minus, 5, start text, space, м, end text
Начальное положение объекта C было 2, start text, space, м, end text, а конечное — 10, start text, space, м, end text. Перемещение объекта C находится по следующей формуле:
delta, x, start subscript, C, end subscript, equals, 10, start text, space, м, end text, minus, 2, start text, м, end text, equals, plus, 8, start text, м, end text
Начальное положение объекта D было 9, start text, space, м, end text, а конечное — 5, start text, space, м, end text. Перемещение объекта D находится по следующей формуле:
delta, x, start subscript, D, end subscript, equals, 5, start text, space, м, end text, minus, 9, start text, space, м, end text, equals, minus, 4, start text, space, м, end text
Пример 2: Расстояние, пройденное каждым из четырёх движущихся объектов
Четыре объекта движутся в соответствии с направлениями, показанными на диаграмме ниже. Предположим, что единицы измерения горизонтальной шкалы даны в метрах. (Изображение предоставлено: с Openstax College Physics, отредактировано)
Какое расстояние преодолел каждый из объектов?
Расстояние, пройденное объектом A, составляет 7, start text, space, м, end text.
Расстояние, пройденное объектом B, составляет 5, start text, space, м, end text.
Расстояние, пройденное объектом C, составляет 8, start text, space, м, end text, plus, 2, start text, space, м, end text, plus, 2, start text, space, м, end text, equals, 12, start text, space, м, end text.
Расстояние, пройденное объектом D, составляет 6, start text, space, м, end text, plus, 2, start text, space, м, end text, equals, 8, start text, space, м, end text.