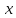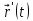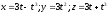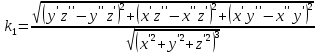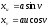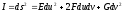Как найти полную кривизну поверхности

Рассматриваем
регулярную поверхность

в окрестности точки
.
Дифференциалы
,

из (3.7.1) подставим в выражение (3.6.4) для
нормальной кривизны поверхности. После
сокращение на

приходим к равенству

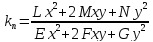
Отсюда
получаем

Дифференцируем
это равенство по

и по
:

Главные
направления в касательной плоскости
определяются этой системой уравнений,
если она имеет ненулевые решения, т.е.
в случае
.

Значение
определителя

Главные
кривизны
,

есть корни выписанного уравнения.
Воспользуемся теоремой Виетта:

,
.

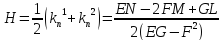
Полная
и средняя кривизны поверхности найдены
без вычисления главных кривизн.

Практическая
часть.

4.Кривая.

Кривая
задана следующим образом:

Найдем
производные первого, второго и третьего
порядков.

4.1.Найдем
уравнение касательной по формуле:

Возьмем
=0;

Найдем
производную

При
подставлении

в

получим точку Р =(0,0,0);

При
подставлении

в

получим точку
=(3,0,3);

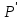
Составим
уравнение касательной для кривой
:

4.2.Найдем
уравнение нормальной плоскости для
кривой

по формуле:

Подставляя
уже найденные ранее данные, получаем:

4.3.Найдем
уравнение соприкасающейся плоскости
по формуле:

Раскроем
определитель по первой строке

—+=0;

Примем

Подставим
значения в уравнение соприкасающейся
плоскости:

Уравнение
соприкасающейся плоскости имеет вид:

8x+6y-3z-1=0.

4.4.Сосчитаем
кривизну кривой

по следующей формуле:

Подставляя
ранее полученные значения производных
первого и второго порядков в основную
формулу нахождения кривизны кривой в
координатах, получим нужную нам кривизну.
Из-за сложности в подсчетах разделим
вычисление на несколько этапов:

Вычисление
числителя без извлечения корня

Приведем
подобные слагаемые и извлечем корень
из получившегося выражения:

2)Вычисление
знаменателя без извлечения корня.

Извлечем
корень

Подставим
все в итоговую формулу

4.5.Вычислим кручение кривой :

Примем
t=0;

Получим
.

4. 6. Изображение кривой.

5. Поверхность.

Поверхность
задана следующим образом:

Вычислим
производные:

5.1. Найдем уравнение касательной плоскости, используя формулу:

Подставляя
в нее значения производных, получим:

Раскроем
определители и получим общее уравнение
искомой поверхности:

Найдем
уравнение касательной плоскости в
конкретной точке:

Выберем
произвольную точку Р(1,2,1).

Зададим
u=1,v=;

Примем
a=2,k=;

Подставляя
в формулу, получим:

5.2. Найдем уравнение нормали для искомой поверхности.

Раскроем
определители:

Подставляя
уже найденные ранее производные и
приводя подобные слагаемые, получим:

Найдем
уравнение нормали в конкретной точке:

Выберем
произвольную точку Р (1,1,2).

Зададим
a=2
,k=,
u=1,v=
;

Подставим
заданные значения в уравнение:

5.3.Вычисление
первой квадратичной формы.

Найдем
частные производные:

Вычисляем
коэффициенты первой квадратичной формы
поверхности:

Детерминант
первой квадратичной формы:

Корень
из детерминанта первой квадратичной
формы:

Первая
квадратичная форма имеет вид:

Подставим
получившиеся значения в эту формулу и
получим

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

From Wikipedia, the free encyclopedia

From left to right: a surface of negative Gaussian curvature (hyperboloid), a surface of zero Gaussian curvature (cylinder), and a surface of positive Gaussian curvature (sphere).

Some points on the torus have positive, some have negative, and some have zero Gaussian curvature.

In differential geometry, the Gaussian curvature or Gauss curvature Κ of a smooth surface in three-dimensional space at a point is the product of the principal curvatures, κ₁ and κ₂, at the given point:

${displaystyle K=kappa _{1}kappa _{2}.}$

The Gaussian radius of curvature is the reciprocal of Κ.
For example, a sphere of radius r has Gaussian curvature 1/r² everywhere, and a flat plane and a cylinder have Gaussian curvature zero everywhere. The Gaussian curvature can also be negative, as in the case of a hyperboloid or the inside of a torus.

Gaussian curvature is an intrinsic measure of curvature, depending only on distances that are measured “within” or along the surface, not on the way it is isometrically embedded in Euclidean space. This is the content of the Theorema egregium.

Gaussian curvature is named after Carl Friedrich Gauss, who published the Theorema egregium in 1827.

Informal definition[edit]

Saddle surface with normal planes in directions of principal curvatures

At any point on a surface, we can find a normal vector that is at right angles to the surface; planes containing the normal vector are called normal planes. The intersection of a normal plane and the surface will form a curve called a normal section and the curvature of this curve is the normal curvature. For most points on most “smooth” surfaces, different normal sections will have different curvatures; the maximum and minimum values of these are called the principal curvatures, call these κ₁, κ₂. The Gaussian curvature is the product of the two principal curvatures Κ = κ₁κ₂.

The sign of the Gaussian curvature can be used to characterise the surface.

If both principal curvatures are of the same sign: κ₁κ₂ > 0, then the Gaussian curvature is positive and the surface is said to have an elliptic point. At such points, the surface will be dome like, locally lying on one side of its tangent plane. All sectional curvatures will have the same sign.
If the principal curvatures have different signs: κ₁κ₂ < 0, then the Gaussian curvature is negative and the surface is said to have a hyperbolic or saddle point. At such points, the surface will be saddle shaped. Because one principal curvature is negative, one is positive, and the normal curvature varies continuously if you rotate a plane orthogonal to the surface around the normal to the surface in two directions, the normal curvatures will be zero giving the asymptotic curves for that point.
If one of the principal curvatures is zero: κ₁κ₂ = 0, the Gaussian curvature is zero and the surface is said to have a parabolic point.

Most surfaces will contain regions of positive Gaussian curvature (elliptical points) and regions of negative Gaussian curvature separated by a curve of points with zero Gaussian curvature called a parabolic line.

Relation to geometries[edit]

When a surface has a constant zero Gaussian curvature, then it is a developable surface and the geometry of the surface is Euclidean geometry.

When a surface has a constant positive Gaussian curvature, then the geometry of the surface is spherical geometry. Spheres and patches of spheres have this geometry, but there exist other examples as well, such as the football.

When a surface has a constant negative Gaussian curvature, then it is a pseudospherical surface and the geometry of the surface is hyperbolic geometry.

Relation to principal curvatures[edit]

The two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions from that point. We represent the surface by the implicit function theorem as the graph of a function, f, of two variables, in such a way that the point p is a critical point, that is, the gradient of f vanishes (this can always be attained by a suitable rigid motion). Then the Gaussian curvature of the surface at p is the determinant of the Hessian matrix of f (being the product of the eigenvalues of the Hessian). (Recall that the Hessian is the 2×2 matrix of second derivatives.) This definition allows one immediately to grasp the distinction between a cup/cap versus a saddle point.

Alternative definitions[edit]

It is also given by

${displaystyle K={frac {{bigl langle }(nabla _{2}nabla _{1}-nabla _{1}nabla _{2})mathbf {e} _{1},mathbf {e} _{2}{bigr rangle }}{det g}},}$

where ∇_i = ∇_{e_i} is the covariant derivative and g is the metric tensor.

At a point p on a regular surface in R³, the Gaussian curvature is also given by

where S is the shape operator.

A useful formula for the Gaussian curvature is Liouville’s equation in terms of the Laplacian in isothermal coordinates.

Total curvature[edit]

The sum of the angles of a triangle on a surface of negative curvature is less than that of a plane triangle.

The surface integral of the Gaussian curvature over some region of a surface is called the total curvature. The total curvature of a geodesic triangle equals the deviation of the sum of its angles from π. The sum of the angles of a triangle on a surface of positive curvature will exceed π, while the sum of the angles of a triangle on a surface of negative curvature will be less than π. On a surface of zero curvature, such as the Euclidean plane, the angles will sum to precisely π radians.

${displaystyle sum _{i=1}^{3}theta _{i}=pi +iint _{T}K,dA.}$

A more general result is the Gauss–Bonnet theorem.

Important theorems[edit]

Theorema egregium[edit]

Gauss’s Theorema egregium (Latin: «remarkable theorem») states that Gaussian curvature of a surface can be determined from the measurements of length on the surface itself. In fact, it can be found given the full knowledge of the first fundamental form and expressed via the first fundamental form and its partial derivatives of first and second order. Equivalently, the determinant of the second fundamental form of a surface in R³ can be so expressed. The «remarkable», and surprising, feature of this theorem is that although the definition of the Gaussian curvature of a surface S in R³ certainly depends on the way in which the surface is located in space, the end result, the Gaussian curvature itself, is determined by the intrinsic metric of the surface without any further reference to the ambient space: it is an intrinsic invariant. In particular, the Gaussian curvature is invariant under isometric deformations of the surface.

In contemporary differential geometry, a «surface», viewed abstractly, is a two-dimensional differentiable manifold. To connect this point of view with the classical theory of surfaces, such an abstract surface is embedded into R³ and endowed with the Riemannian metric given by the first fundamental form. Suppose that the image of the embedding is a surface S in R³. A local isometry is a diffeomorphism f : U → V between open regions of R³ whose restriction to S ∩ U is an isometry onto its image. Theorema egregium is then stated as follows:

The Gaussian curvature of an embedded smooth surface in R³ is invariant under the local isometries.

For example, the Gaussian curvature of a cylindrical tube is zero, the same as for the «unrolled» tube (which is flat).^[1]^{[page needed]} On the other hand, since a sphere of radius R has constant positive curvature R⁻² and a flat plane has constant curvature 0, these two surfaces are not isometric, not even locally. Thus any planar representation of even a small part of a sphere must distort the distances. Therefore, no cartographic projection is perfect.

Gauss–Bonnet theorem[edit]

The Gauss–Bonnet theorem links the total curvature of a surface to its Euler characteristic and provides an important link between local geometric properties and global topological properties.

Surfaces of constant curvature[edit]

Two surfaces which both have constant positive Gaussian curvature but with either an open boundary or singular points.

Minding’s theorem (1839) states that all surfaces with the same constant curvature K are locally isometric. A consequence of Minding’s theorem is that any surface whose curvature is identically zero can be constructed by bending some plane region. Such surfaces are called developable surfaces. Minding also raised the question of whether a closed surface with constant positive curvature is necessarily rigid.
Liebmann’s theorem (1900) answered Minding’s question. The only regular (of class C²) closed surfaces in R³ with constant positive Gaussian curvature are spheres.^[2] If a sphere is deformed, it does not remain a sphere, proving that a sphere is rigid. A standard proof uses Hilbert’s lemma that non-umbilical points of extreme principal curvature have non-positive Gaussian curvature.^[3]
Hilbert’s theorem (1901) states that there exists no complete analytic (class C^ω) regular surface in R³ of constant negative Gaussian curvature. In fact, the conclusion also holds for surfaces of class C² immersed in R³, but breaks down for C¹-surfaces. The pseudosphere has constant negative Gaussian curvature except at its singular cusp.^[4]

There are other surfaces which have constant positive Gaussian curvature. Manfredo do Carmo considers surfaces of revolution where , and ${textstyle psi (v)=int _{0}^{v}{sqrt {1-C^{2}sin ^{2}v'}} dv'}$ (an incomplete Elliptic integral of the second kind). These surfaces all have constant Gaussian curvature of 1, but, for either have a boundary or a singular point. do Carmo also gives three different examples of surface with constant negative Gaussian curvature, one of which is pseudosphere.^[5]

There are many other possible bounded surfaces with constant Gaussian curvature. Whilst the sphere is rigid and can not be bent using an isometry, if a small region removed, or even a cut along a small segment, then the resulting surface can be bent. Such bending preserves Gaussian curvature so any such bending of a sphere with a region removed will also have constant Gaussian curvature.^[6]

Alternative formulas[edit]

Gaussian curvature of a surface in R³ can be expressed as the ratio of the determinants of the second and first fundamental forms II and I:

${displaystyle K={frac {det(mathrm {I!I} )}{det(mathrm {I} )}}={frac {LN-M^{2}}{EG-F^{2}}}.}$
The Brioschi formula (after Francesco Brioschi) gives Gaussian curvature solely in terms of the first fundamental form:

${displaystyle K={frac {{begin{vmatrix}-{frac {1}{2}}E_{vv}+F_{uv}-{frac {1}{2}}G_{uu}&{frac {1}{2}}E_{u}&F_{u}-{frac {1}{2}}E_{v}\F_{v}-{frac {1}{2}}G_{u}&E&F\{frac {1}{2}}G_{v}&F&Gend{vmatrix}}-{begin{vmatrix}0&{frac {1}{2}}E_{v}&{frac {1}{2}}G_{u}\{frac {1}{2}}E_{v}&E&F\{frac {1}{2}}G_{u}&F&Gend{vmatrix}}}{left(EG-F^{2}right)^{2}}}}$
For an orthogonal parametrization (F = 0), Gaussian curvature is:

${displaystyle K=-{frac {1}{2{sqrt {EG}}}}left({frac {partial }{partial u}}{frac {G_{u}}{sqrt {EG}}}+{frac {partial }{partial v}}{frac {E_{v}}{sqrt {EG}}}right).}$
For a surface described as graph of a function z = F(x,y), Gaussian curvature is:^[7]

${displaystyle K={frac {F_{xx}cdot F_{yy}-F_{xy}^{2}}{left(1+F_{x}^{2}+F_{y}^{2}right)^{2}}}}$
For an implicitly defined surface, F(x,y,z) = 0, the Gaussian curvature can be expressed in terms of the gradient ∇F and Hessian matrix H(F):^[8]^[9]

${displaystyle K=-{frac {begin{vmatrix}H(F)&nabla F^{mathsf {T}}\nabla F&0end{vmatrix}}{|nabla F|^{4}}}=-{frac {begin{vmatrix}F_{xx}&F_{xy}&F_{xz}&F_{x}\F_{xy}&F_{yy}&F_{yz}&F_{y}\F_{xz}&F_{yz}&F_{zz}&F_{z}\F_{x}&F_{y}&F_{z}&0\end{vmatrix}}{|nabla F|^{4}}}}$
For a surface with metric conformal to the Euclidean one, so F = 0 and E = G = e^σ, the Gauss curvature is given by (Δ being the usual Laplace operator):

${displaystyle K=-{frac {1}{2e^{sigma }}}Delta sigma .}$
Gaussian curvature is the limiting difference between the circumference of a geodesic circle and a circle in the plane:^[10]

${displaystyle K=lim _{rto 0^{+}}3{frac {2pi r-C(r)}{pi r^{3}}}}$
Gaussian curvature is the limiting difference between the area of a geodesic disk and a disk in the plane:^[10]

${displaystyle K=lim _{rto 0^{+}}12{frac {pi r^{2}-A(r)}{pi r^{4}}}}$
Gaussian curvature may be expressed with the Christoffel symbols:^[11]

${displaystyle K=-{frac {1}{E}}left({frac {partial }{partial u}}Gamma _{12}^{2}-{frac {partial }{partial v}}Gamma _{11}^{2}+Gamma _{12}^{1}Gamma _{11}^{2}-Gamma _{11}^{1}Gamma _{12}^{2}+Gamma _{12}^{2}Gamma _{12}^{2}-Gamma _{11}^{2}Gamma _{22}^{2}right)}$

References[edit]

^ Porteous, I. R. (1994). Geometric Differentiation. Cambridge University Press. ISBN 0-521-39063-X.
^ Kühnel, Wolfgang (2006). Differential Geometry: Curves, Surfaces, Manifolds. American Mathematical Society. ISBN 0-8218-3988-8.
^ Gray, Alfred (1997). «28.4 Hilbert’s Lemma and Liebmann’s Theorem». Modern Differential Geometry of Curves and Surfaces with Mathematica (2nd ed.). CRC Press. pp. 652–654. ISBN 9780849371646..
^ «Hilbert theorem», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
^ Carmo, Manfredo Perdigão do (2016) [First published 1976]. Differential geometry of curves and surfaces (2nd ed.). Mineola, NY: Dover Publications. p. 171. ISBN 978-0-486-80699-0 – via zbMATH.
^ Hilbert, David; Cohn-Vossen, Stephan (1952). Geometry and the Imagination (2nd ed.). Chelsea. p. 228. ISBN 0-8284-1087-9.
^ «General investigations of curved surfaces of 1827 and 1825». [Princeton] The Princeton university library. 1902.
^ Goldman, R. (2005). «Curvature formulas for implicit curves and surfaces». Computer Aided Geometric Design. 22 (7): 632–658. CiteSeerX 10.1.1.413.3008. doi:10.1016/j.cagd.2005.06.005.
^ Spivak, M. (1975). A Comprehensive Introduction to Differential Geometry. Vol. 3. Boston: Publish or Perish.
^ ^a ^b Bertrand–Diquet–Puiseux theorem
^ Struik, Dirk (1988). Lectures on Classical Differential Geometry. Courier Dover Publications. ISBN 0-486-65609-8.

Books[edit]

Grinfeld, P. (2014). Introduction to Tensor Analysis and the Calculus of Moving Surfaces. Springer. ISBN 978-1-4614-7866-9.
Rovelli, Carlo (2021). General Relativity the Essentials. Cambridge University Press. ISBN 978-1-009-01369-7.

External links[edit]

«Gaussian curvature», Encyclopedia of Mathematics, EMS Press, 2001 [1994]

Источник

произведение главных кривизны поверхности Слева направо: поверхность с отрицательной гауссовой кривизной (гиперболоид ), поверхность с нулевой гауссовой кривизной (цилиндр ) и поверхность с положительной гауссовой кривизной (сфера ). Некоторые точки на торе имеют положительные, некоторые отрицательные, а некоторые имеют нулевую гауссову кривизну.

В дифференциальной геометрии, гауссова кривизна или гауссова кривизна Κ поверхности поверхности в точке равна произведение главных кривизны, κ 1 и κ 2 в данной точке:

K = κ 1 κ 2. { displaystyle K = kappa _ {1} kappa _ {2}.} ${ displaystyle K = kappa _ {1} kappa _ {2}. }$

Например, сфера радиуса r имеет гауссову кривизну 1 / r всюду, а плоская плоскость и цилиндр всюду имеют нулевую гауссову кривизну. также может быть отрицательным, как в случае гиперболоида или внутренней части тора.

Гауссия n кривизна — это внутренняя мера кривизны, зависящая только от расстояний, которые измеряются на поверхности, а не от того, как она изометрически встроена в евклидово пространство. Это содержание Теорема egregium.

Гауссова кривизна названа в честь Карла Фридриха Гаусса, опубликовавшего Теорема egregium в 1827 году.

Содержание

1 Неформальное определение
2 Отношение к геометрии
3 Отношение к основным кривизнам
4 Альтернативные определения
5 Полная кривизна
6 Важные теоремы
- 6.1 Теорема egregium
- 6.2 Теорема Гаусса – Бонне
7 Поверхности постоянной кривизны
8 Альтернативные формулы
9 См. Также
10 Ссылки
11 Книги
12 Внешние ссылки

Неофициальное определение

Седловая поверхность с нормальные плоскости в направлениях главных кривизны

В любой точке поверхности мы можем найти вектор нормали , который находится под прямым углом к поверхности; плоскости, содержащие вектор нормали, называются нормальными плоскостями. Пересечение нормальной плоскости и поверхности образует кривую, называемую нормальным сечением, а кривизна этой кривой равна нормальной кривизне. Для большинства точек на большинстве поверхностей разные нормальные сечения будут иметь разную кривизну; их максимальное и минимальное значения называются главными кривизнами, назовем их κ 1, κ 2. Гауссова кривизна является произведением двух основных кривизны Κ = κ 1κ2.

Знак гауссовой кривизны может использоваться для характеристики поверхности.

Если обе главные кривизны имеют один и тот же знак: κ 1κ2>0, то гауссова кривизна положительна и поверхность называется эллиптической. В таких точках поверхность будет иметь куполообразную форму, локально лежащую по одну сторону от своей касательной плоскости. У всех секционных изгибов будет один и тот же знак.
Если главные изгибы имеют разные знаки: κ 1κ2< 0, then the Gaussian curvature is negative and the surface is said to have a hyperbolic or седловая точка. В таких местах поверхность будет иметь форму седла. Поскольку одна основная кривизна отрицательна, другая положительна, а нормальная кривизна непрерывно изменяется, если вы поворачиваете плоскость, ортогональную к поверхности, вокруг нормали к поверхности в двух направлениях, нормальные кривизны будут равны нулю, давая асимптотические кривые для этой точки.
Если одна из главных кривизн равна нулю: κ 1κ2= 0, гауссова кривизна равна нулю и поверхность считается параболической точкой.

Большинство поверхностей будут содержат области положительной гауссовой кривизны (эллиптические точки) и области отрицательной гауссовой кривизны, разделенные кривой точек с нулевой гауссовой кривизной, называемой параболической линией.

Связь с геометрией

Когда поверхность имеет постоянная нулевая гауссова кривизна, тогда это развивающаяся поверхность, а геометрия поверхности — евклидова геометрия.

Когда поверхность имеет постоянную положительную гауссову кривизну, то это сфера и геометрия поверхности сферическая геометрия.

Когда поверхность имеет постоянную отрицательную гауссову кривизну, то это псевдосферическая поверхность, а геометрия поверхности — гиперболическая геометрия.

Отношение к главной кривизне

две основные кривизны в данной точке поверхности являются собственными значениями оператора формы в этой точке. Они измеряют, как поверхность изгибается на разную величину в разных направлениях в этой точке. Мы представляем поверхность по теореме о неявной функции как график функции f двух переменных таким образом, что точка p является критической точкой, то есть градиент f обращается в нуль ( этого всегда можно добиться подходящим жестким движением). Тогда гауссова кривизна поверхности в точке p является определителем матрицы Гессе функции f (являющейся произведением собственных значений гессиана). (Напомним, что гессиан — это матрица вторых производных 2 × 2.) Это определение позволяет сразу уловить различие между чашкой / крышкой и седловой точкой.

Альтернативные определения

Он также задается как

K = ⟨(∇ 2 ∇ 1 — ∇ 1 ∇ 2) e 1, e 2⟩ det g, { displaystyle K = { frac {{ bigl langle} ( nabla _ {2} nabla _ {1} — nabla _ {1} nabla _ {2}) mathbf {e} _ {1}, mathbf { e} _ {2} { bigr rangle}} { det g}},} ${ displaystyle K = { frac {{ bigl langle} ( nabla _ {2} nabla _ { 1} - nabla _ {1} nabla _ {2}) mathbf {e} _ {1}, mathbf {e} _ {2} { bigr rangle}} { det g}},}$

где ∇ i = ∇ ei- ковариантная производная и g — метрический тензор .

В точке p на регулярной поверхности в R гауссова кривизна также определяется как

K (p) = det S (p), { displaystyle K ( mathbf {p}) = det S ( mathbf {p}),}

, где S — оператор формы..

Полезная формула для гауссовой кривизны это уравнение Лиувилля в терминах лапласиана в изотермических координатах.

Полная кривизна

Сумма углов треугольника на поверхности отрицательной кривизны меньше, чем у плоского треугольника.

Поверхностный интеграл гауссовой кривизны по некоторой области поверхности называется общей кривизной . Полная кривизна геодезического треугольника равна отклонению суммы его углов от π. Сумма углов треугольника на поверхности положительной кривизны будет превышать π, а сумма углов треугольника на поверхности отрицательной кривизны будет меньше π. На поверхности нулевой кривизны, такой как евклидова плоскость, сумма углов будет точно равна π радиан.

i = 1 3 θ i = π + ∬ T K d A. { displaystyle sum _ {i = 1} ^ {3} theta _ {i} = pi + iint _ {T} K , dA.} $sum _ {i = 1} ^ {3} theta _ {i} = pi + iint _ {T} K , dA.$

Более общий результат — Gauss –Теорема Бонне.

Важные теоремы

Теорема egregium

Теорема Гаусса egregium (лат. «Замечательная теорема») утверждает, что гауссову кривизну поверхности можно определить по измерениям длины на поверхность сама. Фактически, его можно найти, зная о первой фундаментальной форме , и выразить его через первую фундаментальную форму и ее частные производные первого и второго порядка. Эквивалентно, так может быть выражен детерминант второй фундаментальной формы поверхности в R . «Замечательная» и удивительная особенность этой теоремы состоит в том, что, хотя определение гауссовой кривизны поверхности S в R определенно зависит от того, как поверхность расположена в пространстве, конечный результат, сама гауссова кривизна, определяется внутренней метрикой поверхности без какой-либо дополнительной ссылки на окружающее пространство: это внутренний инвариант. В частности, гауссова кривизна инвариантна относительно изометрических деформаций поверхности.

В современной дифференциальной геометрии «поверхность», рассматриваемая абстрактно, представляет собой двумерное дифференцируемое многообразие. Чтобы связать эту точку зрения с классической теорией поверхностей, такая абстрактная поверхность вложена в R и наделена римановой метрикой дана первая основная форма. Предположим, что образ вложения — это поверхность S в R . Локальная изометрия — это диффеоморфизм f: U → V между открытыми областями R, ограничение которого на S ∩ U является изометрией на его образ. Теорема egregium формулируется следующим образом:

Гауссова кривизна вложенной гладкой поверхности в R инвариантна относительно локальных изометрий.

Например, кривизна по Гауссу цилиндрической трубки равна нулю, так же, как и для «развернутой» трубки (которая является плоской). С другой стороны, поскольку сфера радиуса R имеет постоянную положительную кривизну R, а плоская плоскость имеет постоянную кривизну 0, эти две поверхности не изометричны даже локально. Таким образом, любое плоское изображение даже части сферы должно искажать расстояния. Следовательно, никакая картографическая проекция не идеальна.

Теорема Гаусса – Бонне

Теорема Гаусса – Бонне связывает полную кривизну поверхности с ее эйлеровой характеристикой и обеспечивает важную связь между локальными геометрическими свойствами и глобальной топологической свойства.

Поверхности постоянной кривизны

Теорема Миндинга (1839) утверждает, что все поверхности с одинаковой постоянной кривизной K локально изометричны. Следствием теоремы Миндинга является то, что любую поверхность, кривизна которой тождественно равна нулю, можно построить путем изгибания некоторой плоской области. Такие поверхности называются развертывающимися поверхностями. Миндинг также поднял вопрос, обязательно ли замкнутая поверхность с постоянной положительной кривизной жесткой.
Теорема Либмана (1900) ответила на вопрос Миндинга. Единственные регулярные (класса C) замкнутые поверхности в R с постоянной положительной гауссовой кривизной — это сферы. Если сфера деформируется, она не остается сферой, что доказывает, что сфера жесткая. Стандартное доказательство использует лемму Гильберта о том, что не омбилические точки крайней главной кривизны имеют неположительную гауссову кривизну.
Теорема Гильберта (1901) утверждает, что не существует полной аналитической (класса C) регулярной поверхности в R постоянной отрицательной гауссовой кривизны. Фактически, вывод также верен для поверхностей класса C, погруженных в R, но неверен для C-поверхностей. Псевдосфера имеет постоянную отрицательную гауссову кривизну, за исключением ее сингулярной вершины.

. Альтернативные формулы

гауссовой кривизны поверхности в R можно выразить как отношение детерминанты второй и первой фундаментальных форм II и I:

K = det (II) det (I) = LN — M 2 EG — F 2. { Displaystyle К = { гидроразрыва { det ( mathrm {I ! I})} { det ( mathrm {I})}} = { frac {LN-M ^ {2}} {EG- F ^ {2}}}.} ${ displaystyle K = { frac { det ( mathrm {I ! I})} { det ( mathrm {I})}} = { frac {LN-M ^ {2}} {EG-F ^ {2}}}.}$

Формула Бриоски дает гауссову кривизну исключительно в терминах первой фундаментальной формы:

K = | — 1 2 E v v + F u v — 1 2 G u u 1 2 E u F u — 1 2 E v F v — 1 2 G u E F 1 2 G v F G | — | 0 1 2 E v 1 2 G u 1 2 E v E F 1 2 G u F G | (Пример — F 2) 2 { displaystyle K = { frac {{ begin {vmatrix} — { frac {1} {2}} E_ {vv} + F_ {uv} — { frac {1} { 2}} G_ {uu} { frac {1} {2}} E_ {u} F_ {u} — { frac {1} {2}} E_ {v} \ F_ {v} — { frac {1} {2}} G_ {u} E F \ { frac {1} {2}} G_ {v} F G end {vmatrix}} — { begin {vmatrix} 0 { frac {1} {2}} E_ {v} и { frac {1} {2}} G_ {u} \ { frac {1} {2}} E_ {v} и E F \ { frac {1} {2 }} G_ {u} F G end {vmatrix}}} { left (EG-F ^ {2} right) ^ {2}}}} ${ displaystyle K = { frac {{ begin {vmatrix} - { frac {1} {2} } E_ {vv} + F_ {uv} - { frac {1} {2}} G_ {uu} { frac {1} {2}} E_ {u} и F_ {u} - { frac {1 } {2}} E_ {v} \ F_ {v} - { frac {1} {2}} G_ {u} E F \ { frac {1} {2}} G_ {v} F G end {vmatrix}} - { begin {vmatrix} 0 { frac {1} {2}} E_ {v} { frac {1} {2}} G_ {u} \ { frac {1} { 2}} E_ {v} E F \ { frac {1} {2}} G_ {u} F G end {vmatrix}}} { left (EG-F ^ {2} right) ^ {2} }}}$

Для ортогонального параметризация (F = 0), гауссова кривизна:

K = — 1 2 EG (∂ ∂ u G u EG + ∂ ∂ v E v EG). { displaystyle K = — { frac {1} {2 { sqrt {EG}}}} left ({ frac { partial} { partial u}} { frac {G_ {u}} { sqrt {EG}}} + { frac { partial} { partial v}} { frac {E_ {v}} { sqrt {EG}}} right).} $K = - { frac {1} {2 { sqrt {EG}}}} left ({ frac { partial} { partial u}} { frac {G_ {u}} { sqrt {EG}}} + { frac { partial} { частичный v}} { frac {E_ {v}} { sqrt {EG}}} right).$

Для поверхности, описанной как график функции z = F (x, y), гауссова кривизна:

K = F xx ⋅ F yy — F xy 2 (1 + F x 2 + F y 2) 2 { displaystyle K = { гидроразрыв {F_ {xx} cdot F_ {yy} -F_ {xy} ^ {2}} { left (1 + F_ {x} ^ {2} + F_ {y} ^ {2} right) ^ { 2}}}} ${ displaystyle K = { frac {F_ {xx} cdot F_ {yy} -F_ {xy} ^ {2}} { left (1 + F_ {x} ^ {2} + F_ { y} ^ {2} right) ^ {2}}}}$

Для неявно определенной поверхности F (x, y, z) = 0 гауссова кривизна может быть выражена через градиент ∇F и матрицу Гессе H (F):

K = — | H (F) ∇ F T ∇ F 0 | | ∇ F | 4 = — | F x x F x y F x z F x F x y F y y F y z F y F x z F y z F z z F z F x F y F z 0 | | ∇ F | 4 { displaystyle K = — { frac { begin {vmatrix} H (F) nabla F ^ { mathsf {T}} \ nabla F 0 end {vmatrix}} {| nabla F | ^ {4}}} = — { frac { begin {vmatrix} F_ {xx} F_ {xy} F_ {xz} F_ {x} \ F_ {xy} F_ {yy} F_ {yz} F_ {y} \ F_ {xz} F_ {yz} F_ {zz} F_ {z} \ F_ {x} F_ {y} F_ {z} 0 \ end {vmatrix}} {| nabla F | ^ {4 }}}} ${ displaystyle K = - { frac { begin {vmatrix} H (F) nabla F ^ { mathsf {T}} \ nabla F 0 end {vmatrix}} {| nabla F | ^ {4}}} = - { frac { begin {vmatrix} F_ {xx} F_ {xy} F_ {xz} F_ {x} \ F_ {xy} F_ {yy} F_ {yz} F_ {y} \ F_ {xz} F_ {yz} F_ {zz} F_ {z} \ F_ {x} F_ {y} F_ {z} 0 \ end {vmatrix}} {| nabla F | ^ {4}}}}$

Для поверхности с метрикой, конформной евклидовой, поэтому F = 0 и E = G = e, кривизна Гаусса определяется выражением (Δ — обычный оператор Лапласа ):

K = — 1 2 e σ Δ σ. { Displaystyle K = — { frac {1} {2e ^ { sigma}}} Delta sigma.} ${ displaystyle K = - { frac {1} {2e ^ { sigma}}} Delta sigma.}$

Гауссова кривизна — это предельная разница между окружность геодезической окружности и окружности на плоскости:

K = lim r → 0 + 3 2 π r — C (r) π r 3 { displaystyle K = lim _ {r to 0 ^ {+}} 3 { frac {2 pi rC (r)} { pi r ^ {3}}}} $K = lim _ {r to 0 ^ {+}} 3 { frac {2 pi rC (r)} { pi r ^ {3}}}$

Гауссова кривизна — это предельная разница между область геодезического диска и диска на плоскости:

K = lim r → 0 + 12 π r 2 — A (r) π r 4 { displaystyle K = lim _ { r to 0 ^ {+}} 12 { frac { pi r ^ {2 } -A (r)} { pi r ^ {4}}}} ${ displaystyle K = lim _ {r to 0 ^ {+}} 12 { frac { pi r ^ { 2} -A (r)} { pi r ^ {4}}}}$

Гауссова кривизна может быть выражена с помощью символов Кристоффеля :

K = — 1 E (∂ ∂ u Γ 12 2 — ∂ ∂ v Γ 11 2 + Γ 12 1 Γ 11 2 — Γ 11 1 Γ 12 2 + Γ 12 2 Γ 12 2 — Γ 11 2 Γ 22 2) { displaystyle K = — { frac {1} { E}} left ({ frac { partial} { partial u}} Gamma _ {12} ^ {2} — { frac { partial} { partial v}} Gamma _ {11} ^ {2} + Gamma _ {12} ^ {1} Gamma _ {11} ^ {2} — Gamma _ {11} ^ {1} Gamma _ {12} ^ {2} + Gamma _ { 12} ^ {2} Gamma _ {12} ^ {2} — Gamma _ {11} ^ {2} Gamma _ {22} ^ {2} right)} $K = - { frac { 1} {E}} left ({ frac { partial} { partial u}} Gamma _ {12} ^ {2} - { frac { partial} { partial v}} Gamma _ { 11} ^ {2} + Gamma _ {12} ^ {1} Gamma _ {11} ^ {2} - Gamma _ {11} ^ {1} Gamma _ {12} ^ {2} + Гамма _ {12} ^ {2} Gamma _ {12} ^ {2} - Gamma _ {11} ^ {2} Gamma _ {22} ^ {2} right)$

См. Также

Ссылки

Книги

Гринфельд, П. (2014). Введение в тензорный анализ и исчисление движущихся поверхностей. Springer. ISBN 1-4614-7866-9.

Внешние ссылки

Источник

4.Кривая.

4.5.Вычислим кручение кривой :

4. 6. Изображение кривой.

5. Поверхность.

5.1. Найдем уравнение касательной плоскости, используя формулу:

5.2. Найдем уравнение нормали для искомой поверхности.

Informal definition[edit]

Relation to geometries[edit]

Relation to principal curvatures[edit]

Alternative definitions[edit]

Total curvature[edit]

Important theorems[edit]

Theorema egregium[edit]

Gauss–Bonnet theorem[edit]

Surfaces of constant curvature[edit]

Alternative formulas[edit]

See also[edit]

References[edit]

Books[edit]

External links[edit]

Содержание

Неофициальное определение

Связь с геометрией

Отношение к главной кривизне

Альтернативные определения

Полная кривизна

Важные теоремы

Теорема egregium

Теорема Гаусса – Бонне

Поверхности постоянной кривизны

. Альтернативные формулы

См. Также

Ссылки

Книги

Внешние ссылки

Не пропустите также: