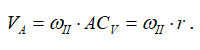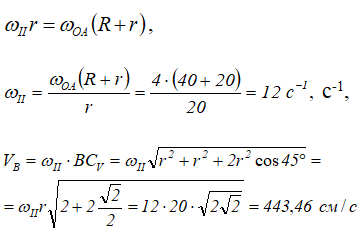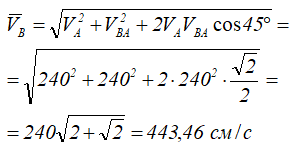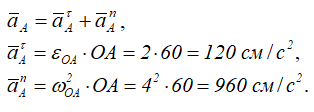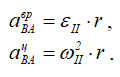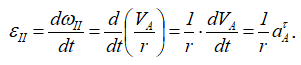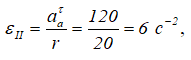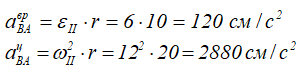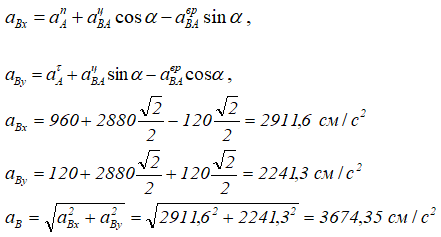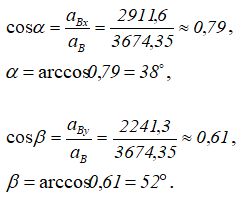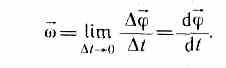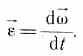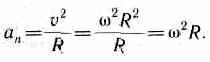Как найти полное ускорение точки на ободе

Пример решения задачи по определению величины и направления скорости и полного ускорения точки колеса, для момента времени, когда угол будет равен заданному значению.

Задача

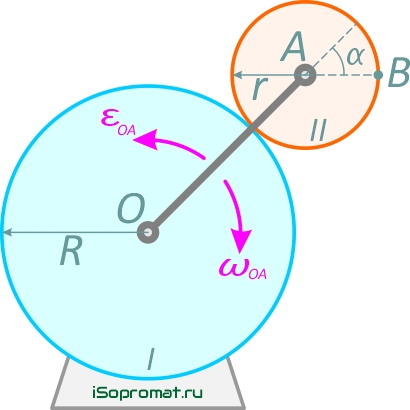
Кривошип ОА, вращаясь вокруг оси, перпендикулярной плоскости чертежа и проходящей через точку О, приводит в движение колесо II, которое катится без скольжения по неподвижному колесу I.

Рис. 2

Найти скорость и ускорение точки В колеса II, для момента времени, когда угол α=45°,
если R=40 см, r=20 см, ω_OA=4 с^-1, ε_OA=2 с^-2 (рис. 2).

Другие примеры решений >
Помощь с решением задач >

Решение

Теория по теме

Колесо II движется в плоскости чертежа, т.е. совершает плоскопараллельное движение.

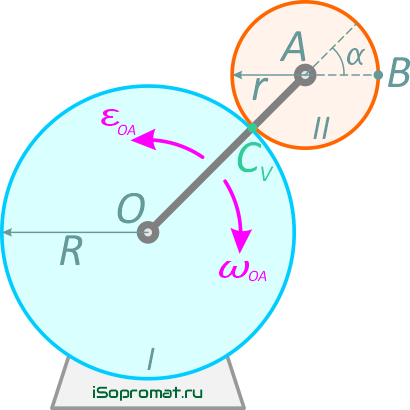
По условию, колесо I неподвижно, значит, точка соприкосновения колес является МЦС для колеса II.

Рис. 2.10

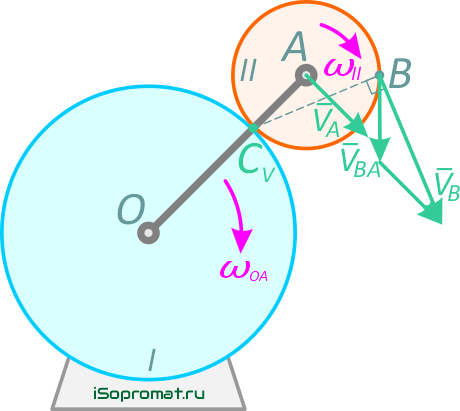
Обозначим ее как C_V (эта точка не принадлежит кривошипу ОА). Скорость точки В определяется выражением

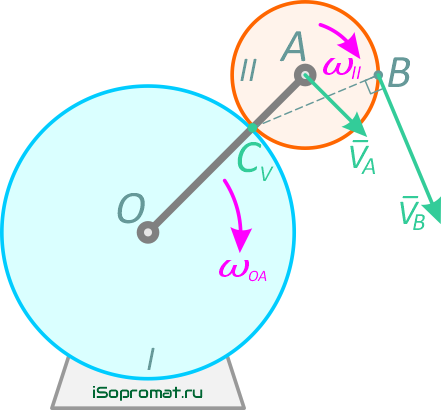
и направлена перпендикулярно отрезку ВС_V, в сторону вращения колеса II (рис. 2.11)

Рис. 2.11

Для определения угловой скорости ω_II запишем выражение для скорости точки А.

С другой стороны, точка А принадлежит кривошипу ОА. Скорость точки А, принадлежащей кривошипу, определяется выражением

и направлена ⊥ОА в сторону вращения кривошипа ОА. Из этих рассуждений следует:

Найдем скорость точки В, используя теорему о скоростях точек плоской фигуры. Для этого примем точку А за полюс.

Тогда

Величина и направление скорости точки А определяются из условий движения кривошипа ОА.
V_A=ω_OA×OA
и вектор V_A⊥ОА и направлен в сторону вращения кривошипа (рис. 2.12).

Рис. 2.12

Скорость V_BA — это скорость точки В во вращательном движении вокруг полюса А.

Величина скорости
V_BA=ω_II×r=12×20=240 см/с
и этот вектор направлен ⊥ отрезку АВ в сторону вращения колеса II.

Чтобы сложить V_A и V_BA, перенесем вектор V_A в конец вектора V_BA. Соединяя начало вектора V_BA с концом вектора V_A, получим вектор V_B. Из построения:

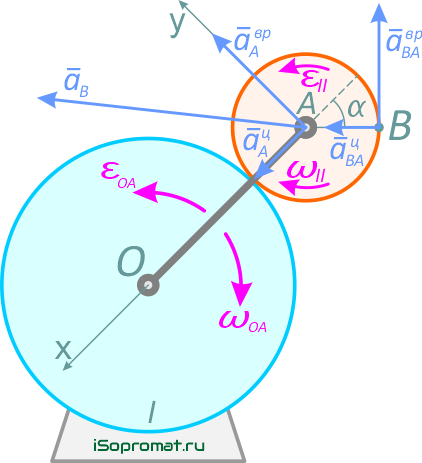
Определим ускорение точки В.

Согласно теореме об ускорении точки плоской фигуры, ускорение точки В можно определить из выражения

где a_A — ускорение точки А, принятой за полюс;

a_BA — ускорение точки В во вращательном движении, вокруг полюса А.

Рис. 2.13

Точка А – принадлежит колесу II и кривошипу ОА, движение которого известно, тогда

Ускорение a_BA (ускорение во вращательном движении) состоит из двух слагаемых:

где

Найдем ε_II по определению:

Подставляя числовые значения, получим

тогда

Ускорение точки В найдем, спроецировав все векторы уравнения

на выбранные оси координат ОХ и OY.

Углы, которые составляют вектор ускорения a_B с осями ОХ и OY, определим через направляющие косинусы.

Скорость и ускорение точки В колеса II, для момента времени, когда угол α=45° найдены.

Другие примеры решения задач >

0 Пользователей и 1 Гость просматривают эту тему.

Прошло 8 месяцев, и родилось решение.

В формуле f = 0,5 + 1,5t + 0,5t² не указано время измерения t. Пусть время измеряется в секундах.

Обозначения: v — линейная скорость, a — линейное ускорение (которое необходимо найти); a_tang — тангенциальное ускорение, a_norm — центростремительное ускорение, f — угол поворота (в радианах), w — угловая скорость, e — угловое ускорениe, f’ (t) — производная от f по t, f» (t) — вторая производная, R — радиус вращательного движения.

Тогда:   w = f’ (t) = 1,5 + t;

e = f» (t) = 1;

a_tang = wR;

a_norm = v²/R.

Далее вычислены значения величин при t = 3 с:

w = 4,5 рад/с;

e = 1 рад/с²;

a_tang = 1 м/с²;

a_norm = 4,5² × 1 = 20,25 м/с².

Поскольку a_tang и a_norm — значения векторов, направленных перпендикулярно друг к другу, значение полного ускорения находим по формуле теоремы Пифагора:
a = √(2,25² + 1) = 20,27 м/с².

Ответ: через 3 с полное ускорение будет равно 20,27 м/с².

Рассмотрим
твердое тело, которое враща­ется
вокруг неподвижной оси. Тогда от­дельные
точки этого тела будут описывать
окружности разных радиусов, центры
ко­торых лежат на оси вращения. Пусть
не­которая точка движется по окружности
радиуса R
(рис.6).
Ее положение через промежуток времени
t
зададим
углом .
Элементарные (бесконечно малые) углы
поворота рассматривают как векторы.
Мо­дуль вектора d
равен
углу поворота, а его направление совпадает
с направле­нием поступательного
движения острия винта, головка которого
вращается в на­правлении движения
точки по окружности, т. е. подчиняется
правилу
правого, винта (рис.6).
Векторы, направления которых связываются
с направлением вращения, называются
псевдовекторами
или
акси­альными
векторами. Эти
векторы не имеют определенных точек
приложения: они мо­гут откладываться
из любой точки оси вращения.

Угловой
скоростью называется
вектор­ная величина, равная первой
производной угла поворота тела по
времени:

Вектор
«в направлен вдоль оси вращения по
правилу правого винта, т. е. так же, как
и вектор d
(рис. 7). Размерность угловой скорости
dim=T^-1,
a .
ее единица — радиан в секунду (рад/с).

Линейная скорость
точки (см. рис. 6)

В векторном виде
формулу для линейной скорости можно
написать как вектор­ное произведение:

При
этом модуль векторного произведе­ния,
по определению, равен

,
а
направление совпадает с
направлением
поступательного движения правого винта
при его вращении от 
к R.

Если
=const,
то
вращение равномер­ное и его можно
характеризовать перио­дом
вращения Т
—
временем, за которое точка совершает
один полный оборот, т. е. поворачивается
на угол 2.
Так как промежутку времени t=T
соответствует =2,
то =
2/Т,
откуда

Число
полных оборотов, совершаемых телом при
равномерном его движении по окружности,
в единицу времени называет­ся частотой
вращения:

Угловым
ускорением называется
век­торная величина, равная первой
производ­ной угловой скорости по
времени:

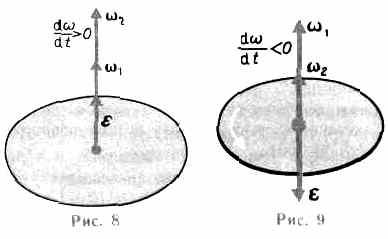
При вращении тела
вокруг неподвижной оси вектор углового
ускорения направлен вдоль оси вращения
в сторону вектора элементарного
приращения угловой ско­рости. При
ускоренном движении вектор

13

 сонаправлен
вектору 
(рис.8),
при замедленном.— противонаправлен
ему (рис. 9).

Тангенциальная
составляющая ускорения

Нормальная
составляющая ускорения

Таким
образом, связь между линейны­ми (длина
пути s,
пройденного
точкой по дуге окружности радиуса R,
линейная
ско­рость v,
тангенциальное
ускорение а_,
нор­мальное ускорение а_n)
и угловыми величи­нами (угол поворота
,
угловая скорость (о, угловое ускорение
)
выражается сле­дующими формулами:

В
случае равнопеременного движения точки
по окружности (=const)

где
₀
— начальная угловая скорость.

Контрольные
вопросы

• Что
называется материальной точкой? Почему
в механике вводят такую модель?

• Что
такое система отсчета?

• Что
такое вектор перемещения? Всегда ли
модуль вектора перемещения равен отрезку
пути,

пройденному точкой?

• Какое
движение называется поступательным?
вращательным?

• Дать
определения векторов средней скорости
и среднего ускорения, мгновенной
скорости

и мгновенного
ускорения. Каковы их направления?

• Что
характеризует тангенциальная
составляющая ускорения? нормальная
составляющая

ускорения? Каковы
их модули?

• Возможны
ли движения, при которых отсутствует
нормальное ускорение? тангенциальное

ускорение? Приведите
примеры.

• Что
называется угловой скоростью? угловым
ускорением? Как определяются их
направления?

• Какова
связь между линейными и угловыми
величинами?

Задачи

1.1.
Зависимость
пройденного телом пути от времени
задается уравнением s
= A+Вt+Сt²+Dt³
(С
= 0,1 м/с²,
D
= 0,03 м/с³).
Определить: 1) через какое время после
начала движения ускорение а тела будет
равно 2 м/с²;
2) среднее ускорение <а>
тела за этот промежуток времени. [ 1) 10
с; 2) 1,1 м/с²]

1.2.
Пренебрегая сопротивлением воздуха,
определить угол, под которым тело брошено
к гори­зонту, если максимальная высота
подъема тела равна 1/4 дальности его
полета. [45°]

1.3.
Колесо
радиуса R
=
0,1 м вращается так, что зависимость
угловой скорости от времени задается
уравнением 
= 2At+5Вt⁴
(A=2
рад/с²
и B=1
рад/с⁵).
Определить полное ускорение точек обода
колеса через t=1
с после начала вращения и число оборотов,
сделан­ных колесом за это время. [а =
8,5 м/с²;
N
= 0,48]

14

1.4.
Нормальное ускорение точки, движущейся
по окружности радиуса r=4
м,
задается уравнением а_n=А+-Bt+Ct²
(A=1
м/с²,
В=6
м/с³,
С=3
м/с⁴).
Определить: 1) тангенциальное ускорение
точки; 2) путь, пройденный точкой за время
t₁=5
с после начала движения; 3) полное
ускорение для момента времени t₂=1
с. [ 1) 6 м/с²;
2) 85 м; 3) 6,32 м/с²]

1.5.
Частота
вращения колеса при равнозамедленном
движении за t=1
мин
уменьшилась от 300 до 180 мин^-1.
Определить: 1) угловое ускорение колеса;
2) число полных оборотов, сделанных
колесом за это время. [1)
0,21 рад/с²;
2) 360]

1.6.
Диск
радиусом R=10
см вращается вокруг неподвижной оси
так, что зависимость угла поворота
радиуса диска от времени задается
уравнением =A+Bt+Ct²+Dt³
(B
= l рад/с,
С=1
рад/с²,
D=l
рад/с³).
Определить для точек на ободе колеса к
концу второй секунды после начала
движения: 1) тангенциальное ускорение
а_;
2) нормальное ускорение а_n;
3) полное ускорение а. [ 1) 0,14 м/с²;
2) 28,9 м/с²;
3) 28,9 м/с²]

Соседние файлы в папке Трофимова

• #
• #
• #
• #
• #
• #

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Определить полное ускорение точки (29 ноября 2009)

Механика. Молекулярная физика. Термодинамика. Б. А. Фёдоров.

• версия для печати
• Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Комментарии

• Войдите или зарегистрируйтесь, чтобы отправлять комментарии

• Войдите или зарегистрируйтесь, чтобы отправлять комментарии

• Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Начальная скорость точки равна нулю, поэтому изменение ее скорости:

Средняя скорость точки равна:

С другой стороны, v_cp = (v − v_o) / 2 = (1/2) v.

Тогда Δt = 2пR / v.

Нормальное ускорение равно:

Полное ускорение точки:

Подставляя числовые данные, получим:

• Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Можно было найти скорость в конечной точке через

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.

Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

Если угол поворота мал, то ∆ l ≈ ∆ s .

Угловая скорость

При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.

Определение. Угловая скорость

Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .

ω = ∆ φ ∆ t , ∆ t → 0 .

Единица измерения угловой скорости — радиан в секунду ( р а д с ).

Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:

Нормальное ускорение

При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.

При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.

a n = ∆ v → ∆ t , ∆ t → 0

Модуль центростремительного ускорения можно вычислить по формуле:

a n = v 2 R = ω 2 R

Докажем эти соотношения.

Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .

В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.

По определению ускорения:

a → = ∆ v → ∆ t , ∆ t → 0

Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .

Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:

R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R

При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:

a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .

При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.

Запись центростремительного ускорения в векторной форме выглядит следующим образом:

Здесь R → — радиус вектор точки на окружности с началом в ее центре.

Тангенциальное ускорение

В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.

Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.

a τ = ∆ v τ ∆ t ; ∆ t → 0

Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t

Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .

Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω