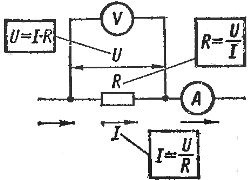
Как найти полное напряжение всего участка цепи - Avtoru.top

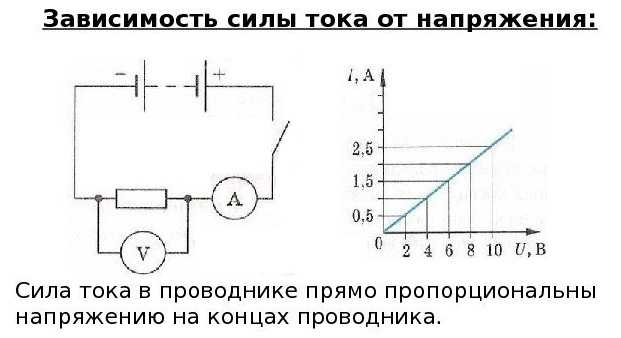
Закон Ома для участка цепи и полной цепи: формулы и определения

Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.

Закон Ома для участка цепи:

Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.

I — сила тока (в системе СИ измеряется — Ампер)
- Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
- Формула: I=frac
- U — напряжение (в системе СИ измеряется — Вольт)
  - Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
  - Формула: U=IR
- R— электрическое сопротивление (в системе СИ измеряется — Ом).
  - Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
  - Формула R=frac

Определение единицы сопротивления — Ом

1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1 (Вольт) протекает ток 1 (Ампер).

Закон Ома для полной цепи

Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника

Формула I=frac <varepsilon>

varepsilon — ЭДС источника напряжения, В;
I — сила тока в цепи, А;
R — сопротивление всех внешних элементов цепи, Ом;
r — внутреннее сопротивление источника напряжения, Ом.

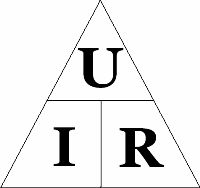
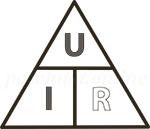
Как запомнить формулы закона Ома

Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.

U — электрическое напряжение;
I — сила тока;
P — электрическая мощность;
R — электрическое сопротивление

Смотри также:

Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.

Источник

Закон Ома для участка цепи

Основным законом электротехники, при помощи которого можно изучать и рассчитывать электрические цепи, является закон Ома, устанавливающий соотношение между током, напряжением и сопротивлением. Необходимо отчетливо понимать его сущность и уметь правильно пользоваться им при решении практических задач. Часто в электротехнике допускаются ошибки из-за неумения правильно применить закон Ома.

Закон Ома для участка цепи гласит: ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.

Если увеличить в несколько раз напряжение, действующее в электрической цепи, то ток в этой цепи увеличится во столько же раз. А если увеличить в несколько раз сопротивление цепи, то ток во столько же раз уменьшится. Подобно этому водяной поток в трубе тем больше, чем сильнее давление и чем меньше сопротивление, которое оказывает труба движению воды.

В популярной форме этот закон можно сформулировать следующим образом: чем выше напряжение при одном и том же сопротивлении, тем выше сила тока и в то же время чем выше сопротивление при одном и том же напряжении, тем ниже сила тока.

Чтобы выразить закон Ома математически наиболее просто, считают, что сопротивление проводника, в котором при напряжении 1 В проходит ток 1 А, равно 1 Ом.

Ток в амперах можно всегда определить, если разделить напряжение в вольтах на сопротивление в омах. Поэтому закон Ома для участка цепи записывается следующей формулой:

Любой участок или элемент электрической цепи можно охарактеризовать при помощи трёх характеристик: тока, напряжения и сопротивления.

Как использовать треугольник Ома: закрываем искомую величину — два других символа дадут формулу для её вычисления. Кстати, законом Ома называется только одна формула из треугольника – та, которая отражает зависимость тока от напряжения и сопротивления. Две другие формулы, хотя и являются её следствием, физического смысла не имеют.

Расчеты, выполняемые с помощью закона Ома для участка цепи, будут правильны в том случае, когда напряжение выражено в вольтах, сопротивление в омах и ток в амперах. Если используются кратные единицы измерений этих величин (например, миллиампер, милливольт, мегаом и т. д.), то их следует перевести соответственно в амперы, вольты и омы. Чтобы подчеркнуть это, иногда формулу закона Ома для участка цепи пишут так:

Можно также рассчитывать ток в миллиамперах и микроамперах, при этом напряжение должно быть выражено в вольтах, а сопротивление — в килоомах и мегаомах соответственно.

Другие статьи про электричество в простом и доступном изложении:

Закон Ома справедлив для любого участка цепи. Если требуется определить ток в данном участке цепи, то необходимо напряжение, действующее на этом участке (рис. 1), разделить на сопротивление именно этого участка.

Рис 1. Применение закона Ома для участка цепи

Приведем пример расчета тока по закону Ома . Пусть требуется определить ток в лампе, имеющей сопротивление 2,5 Ом, если напряжение, приложенное к лампе, составляет 5 В. Разделив 5 В на 2,5 Ом, получим значение тока, равное 2 А. Во втором примере определим ток, который будет протекать под действием напряжения 500 В в цепи, сопротивление которой равно 0,5 МОм. Для этого выразим сопротивление в омах. Разделив 500 В на 500 000 Ом, найдем значение тока в цепи, которое равно 0,001 А или 1 мА.

Часто, зная ток и сопротивление, определяют с помощью закона Ома напряжение. Запишем формулу для определения напряжения

Из этой формулы видно, что напряжение на концах данного участка цепи прямо пропорционально току и сопротивлению . Смысл этой зависимости понять нетрудно. Если не изменять сопротивление участка цепи, то увеличить ток можно только путем увеличения напряжения. Значит при постоянном сопротивлении большему току соответствует большее напряжение. Если же надо получить один и тот же ток при различных сопротивлениях, то при большем сопротивлении должно быть соответственно большее напряжение.

Напряжение на участке цепи часто называют падением напряжения . Это нередко приводит к недоразумению. Многие думают, что падение напряжения есть какое-то потерянное ненужное напряжение. В действительности же понятия напряжение и падение напряжения равнозначны. Потери и падение напряжения — в чем различие?

Падение напряжения — постепенное падение потенциала вдоль цепи, по которой течет ток, обусловленное тем, что цепь обладает активным сопротивлением. По закону Ома падение напряжения в каком-либо участке цепи U равно произведению сопротивления этого участка цепи R на силу тока в нем I , т. е. U — RI. Таким образом, чем больше сопротивление участка цепи, тем больше падение напряжения в этом участке цепи при данной силе тока.

Расчет напряжения с помощью закона Ома можно показать на следующем примере. Пусть через участок цепи с сопротивлением 10 кОм проходит ток 5 мА и требуется определить напряжение на этом участке.

Умножив I = 0,005 А на R — 10 000 Ом, получим напряжение,равное 5 0 В. Можно было бы получить тот же результат, умножив 5 мА на 10 кОм: U = 50 В

В электронных устройствах ток обычно выражается в миллиамперах, а сопротивление — в килоомах. Поэтому удобно в расчетах по закону Ома применять именно эти единицы измерений.

По закону Ома рассчитывается также сопротивление, если известно напряжение и ток. Формула для этого случая пишется следующим образом: R = U/I.

Сопротивление всегда представляет собой отношение напряжения к току. Если напряжение увеличить или уменьшить в несколько раз, то ток увеличится или уменьшится в такое же число раз. Отношение напряжения к току, равное сопротивлению, остается неизменным.

Не следует понимать формулу для определения сопротивления в том смысле, что сопротивление данного проводника зависит оттока и напряжения. Известно, что оно зависит от длины, площади сечения и материала проводника. По внешнему виду формула для определения сопротивления напоминает формулу для расчета тока, но между ними имеется принципиальная разница.

Ток в данном участке цепи действительно зависит от напряжения и сопротивления и изменяется при их изменении. А сопротивление данного участка цепи является величиной постоянной, не зависящей от изменения напряжения и тока, но равной отношению этих величин.

Когда один и тот же ток проходит в двух участках цепи, а напряжения, приложенные к ним, различны, то ясно, что участок, к которому приложено большее напряжение, имеет соответственно большее сопротивление.

А если под действием одного и того же напряжения в двух разных участках цепи проходит различный ток, то меньший ток всегда будет на том участке, который имеет большее сопротивление. Все это вытекает из основной формулировки закона Ома для участка цепи, т. е. из того, что ток тем больше, чем больше напряжение и чем меньше сопротивление.

Расчет сопротивления с помощью закона Ома для участка цепи покажем на следующем примере. Пусть требуется найти сопротивление участка, через который при напряжении 40 В проходит ток 50 мА. Выразив ток в амперах, получим I = 0,05 А. Разделим 40 на 0,05 и найдем, что сопротивление составляет 800 Ом.

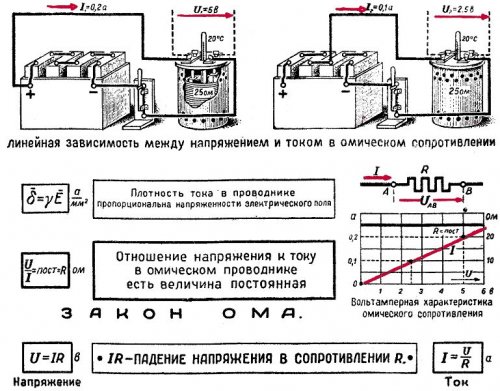
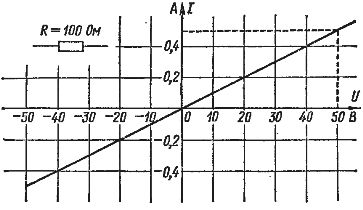
Закон Ома можно наглядно представить в виде так называемой вольт-амперной характеристики . Как известно, прямая пропорциональная зависимость между двумя величинами представляет собой прямую линию, проходящую через начало координат. Такую зависимость принято называть линейной .

На рис. 2 показан в качестве примера график закона Ома для участка цепи с сопротивлением 100 Ом. По горизонтальной оси отложено напряжение в вольтах, а по вертикальной оси — ток в амперах. Масштаб тока и напряжения может быть выбран каким угодно. Прямая линия проведена так, что для любой ее точки отношение напряжения к току равно 100 Ом. Например, если U = 50 В, то I = 0,5 А и R = 50 : 0,5 = 100 Ом.

Рис. 2 . Закон Ома (вольт-амперная характеристика)

График закона Ома для отрицательных значений тока и напряжения имеет такой же вид. Это говорит о том, что ток в цепи проходит одинаково в обоих направлениях. Чем больше сопротивление, тем меньше получается ток при данном напряжении и тем более полого идет прямая.

Приборы, у которых вольт-амперная характеристика является прямой линией, проходящей через начало координат, т. е. сопротивление остается постоянным при изменении напряжения или тока, называются линейными приборами . Применяют также термины линейные цепи, линейные сопротивления.

Существуют также приборы, у которых сопротивление изменяется при изменении напряжения или тока. Тогда зависимость между током и напряжением выражается не по закону Ома, а более сложно. Для таких приборов вольт-амперная характеристика не будет прямой линией, проходящей через начало координат, а является либо кривой, либо ломаной линией. Эти приборы называются нелинейными .

Источник

Закон Ома для участка цепи: формула. Зависимость силы тока от напряжения

Закон Ома для участка цепи — одна из основ электротехники. Данный закон указывает на соотношение между током, напряжением и сопротивлением.

Сам Закон Ома для участка цепи гласит так:

Сила тока в проводнике (участке электрической цепи) прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника (участка электрической цепи)

Из этого определения Георг Ом вывел следующую формулу:

Формула, вытекающая из закона Ома, также известна в просторечии как формула URI. Такое название появилось от последовательности букв в формуле:

R — сопротивление проводника (Ом);
I — сила тока в проводнике (Ампер);
U — напряжение приложенное к проводнику (Вольт).

Электрическая цепь и закон Ома

Три величины — напряжение, электрический ток и сопротивление — могут быть четко представлены в электрической цепи. В простейшем случае она состоит из источника постоянного напряжения и резистора. Резистор подключен к источнику напряжения, а для упрощения возьмем, что сопротивление проводов равно 0 Ом.

Рис. 1. Электрическая цепь

Направление электрического тока.

В электротехнике ток течет от плюса до минуса (смотрите рисунок 1). Другими словами, как только возникает замкнутая цепь, ток начинает течь от положительного полюса к отрицательному полюсу источника напряжения. Мы говорим о замкнутой цепи, когда два полюса источника напряжения соединены друг с другом сопротивлением.

Как и чем измерять ток и напряжение?

Есть два способа определения силы тока и напряжения. С одной стороны, их можно определить арифметически с помощью закона Ома для участка цепи. С другой стороны, две переменные также могут быть определены путем измерения.

Однако для арифметического определения тока или напряжения должны быть известны две другие величины (напряжение и сопротивление либо ток и сопротивление).

С другой стороны, метрологический метод также работает с любой электрической цепью. Для этого в электрическую цепь необходимо вставить амперметр и вольтметр . Они используются для измерения силы тока и напряжения. Но здесь также применяется закон Ома, поскольку сопротивление нельзя измерить напрямую, но его можно будет рассчитать, когда будут измерены значения тока и напряжения.

Итак, ток измеряется так амперметром, который последовательно подключается к потребителю (резистору, лампе накаливания и т. д.), Через который нужно определять ток. На принципиальной схеме он изображен как A внутри круга (см. рисунок 1). Амперметр имеет очень низкое внутреннее сопротивление, чтобы не влиять на ток, который должен протекать через потребителя. В идеале, внутреннее сопротивление амперметра принимается равным 0 Ом и поэтому просто опускается.

Измерение напряжения производится с помощью вольтметра, который замеряет разность потенциалов между двумя его точками подключения. На электрической схеме он обозначен буквой V внутри круга (см. рисунок 1). В отличие от амперметра, вольтметр подключается параллельно нагрузке, на которой измеряется напряжение. Добавление вольтметра параллельно некоторому потребителю (например, резистору) создает току еще один «обходной» путь, что резко изменяет параметры цепи. Чтобы избежать этих нежелательных последствий, надо применять вольтметры с максимально большим сопротивлением.

Вольт-амперная характеристика (ВАХ).

Вольт-амперная характеристика или характеристика UI резистора может быть записана путем приложения к нему различных напряжений и последующего измерения тока. Обычно при омическом сопротивлении достаточно одной точки измерения, которая затем соединяется с началом системы координат. Однако на практике, для целей контроля, выполняют серию измерений с тремя точками измерения.

Затем эти точки измерения отмечаются в системе координат и соединяются. Напряжение откладывают по оси абсцисс, а ток — по оси ординат. Пример ВАХ смотрите на рисунке ниже

ВАХ может быть использована для определения тока через резистор при определенном напряжении.

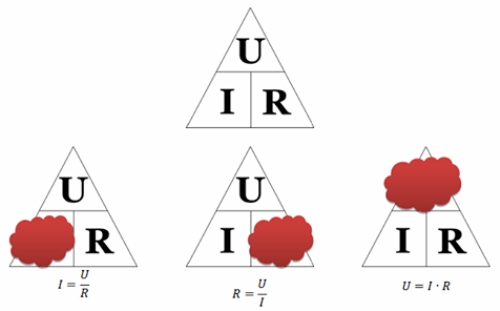
«Треугольник Ома»

Связь между отдельными величинами из закона Ома может быть показана в так называемом «треугольнике Ома».

Вверху треугольника вы найдете напряжение U, слева — сопротивление R, а справа — ток I.

Треугольник Ома

Если вы хотите определить недостающую величину, то прикройте эту величину мысленно или пальцем, а затем посмотрите на две другие величины. Если две «не закрытые» величины находятся рядом друг с другом, то они умножаются. С другой стороны, если они расположены друг над другом, то верхняя величина делится на нижнюю.

Например, вы «закрываете» напряжение U в вершине «треугольника Ома». Две оставшиеся величины, то есть сопротивление R и ток I, находятся рядом. Соответственно, чтобы получить напряжение U, нужно умножить сопротивление R на ток I. Это в точности соответствует формуле закона Ома для участка электрической цепи.

Калькулятор, который основан на законе Ома

Используйте этот калькулятор, который основан на законе Ома для расчета соотношений между током, напряжением, сопротивлением и мощностью в электрических цепях. Чтобы воспользоваться калькулятором, введите значения в 2 любых поля и нажмите кнопку «рассчитать».

Источник

Закон
Ома для участка цепи: сила
тока I
на участке электрической цепи прямо
пропорциональна напряжению U
на концах участка и обратно пропорциональна
его сопротивлению
R.

Формула
закона:

I=.
Отсюда запишем формулыU= IR
и R
=.

Рис.1.Участок
цепи
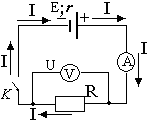
Рис.2.Полная
цепь

Закон
Ома для полной цепи: сила
тока I
полной электрической цепи равна
ЭДС
(электродвижущей силе) источника тока
Е,
деленной на полное сопротивление цепи
(R
+ r). Полное
сопротивление цепи равно сумме
сопротивлений внешней цепи R
и внутреннего r
источника тока.
Формула
закона I
=

.
На
рис. 1 и 2 приведены схемы электрических
цепей.

3. Последовательное и параллельное соединение проводников

Проводники
в электрических цепях могут соединяться
последовательно
и параллельно.
Смешанное соединение сочетает оба эти
соединения.

Сопротивление,
при
включении которого
вместо всех других проводников,
находящихся между двумя точками цепи,
ток и напряжение остаются неизменными,
называют
эквивалентным
сопротивлением
этих
проводников.

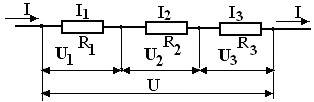
Последовательное соединение

Последовательным
называется соединение, при котором
каждый
проводник соединяется только с одним
предыдущим и одним последующим
проводниками.

Как
следует из первого правила
Кирхгофа,
при последовательном
соединении проводников сила электрического
тока, протекающего по всем проводникам,
одинакова (на основании закона сохранения
заряда).

1.
При последовательном соединении
проводников
(рис. 1)
сила
тока во всех проводниках одинакова:
I₁ = I₂ =
I₃=
I

Рис.
1.
Последовательное
соединение двух проводников.

2.
Согласно закону Ома, напряжения
U₁
и
U₂
на
проводниках равны U₁ = IR₁, U₂ = IR₂,
U₃ = IR₃.

Напряжение
при последовательном соединении
проводников равно сумме напряжений на
отдельных участках (проводниках)
электрической цепи.

U = U₁+U₂ + U₃

По
закону
Ома, напряжения U_1,
U₂
на
проводниках равны
U₁ = IR₁, U₂ = IR₂,
В
соответствии вторым правилом Кирхгофа
напряжение на всем участке:

U = U₁+U₂ =
IR₁+ IR₂
=
I(R₁+
R₂)=
I·R.

Получаем:
R =
R₁ + R₂

Общее
напряжение U
на проводниках равно сумме напряжений
U₁,
U_{2

,}U₃
равно: U =
U₁ + U₂ + U₃ = I·(R₁ + R₂+ R₃)
= IR

где
R_ЭКВ
–
эквивалентное
сопротивление всей цепи. Отсюда: R_ЭКВ=
R₁ + R₂ + R₃

При
последовательном соединении эквивалентное
сопротивление цепи равно сумме
сопротивлений отдельных участков цепи:
R _ЭКВ=
R₁ + R₂ + R₃+…

Этот
результат справедлив для
любого числа
последовательно соединенных проводников.

Из
закона Ома
следует:
при равенстве сил тока при последовательном
соединении:

I = ,I = .
Отсюда
= или

=,
т. е. напряжения на отдельных участках
цепи прямо пропорциональны сопротивлениям
участков.

При
последовательном соединении n
одинаковых
проводников общее напряжение равно
произведению напряжению одного U₁на
их количество n:

U_ПОСЛЕД=
n
·U₁.
Аналогично
для сопротивлений:

R_ПОСЛЕД
= n·
R₁

При размыкании
цепи одного из последовательно
соединенных потребителей ток исчезает
во всей цепи, поэтому последовательное
соединение на практике не всегда удобно.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Чтобы хоть немного разбираться в электрике, необходимо знать основополагающие законы. Один из них — закон Ома. С него начинают изучение электрики и не зря. Он иллюстрирует зависимость параметров электрической цепи друг от друга.

Содержание статьи

1 Как звучит закон Ома для участка цепи
2 Разбираемся что такое ток и сопротивление
3 Говорим о напряжении
4 Что изменится для полной цепи
5 Как найти сопротивление, напряжение
6 Параллельное и последовательное соединение
- 6.1 Последовательное соединение
- 6.2 Параллельное соединение
- 6.3 Что нам дает параллельное и последовательное соединение?

Как звучит закон Ома для участка цепи

Есть говорить об официальной формулировке, то закон Ома можно озвучить так:

Сила тока имеет прямую зависимость от напряжения и обратную от сопротивления. Это высказывание справедливо для участка цепи с каким-то определенным и стабильным сопротивлением.

Формула этой зависимости на рисунке. Тут I — это сила тока, U — напряжение, R — сопротивление.

Формула закона Ома

Чем больше напряжение, тем больше ток.

Чем больше сопротивление, тем ток меньше.

Не так легко представить себе смысл этого выражения. Ведь электричество нельзя увидеть. Мы только приблизительно знаем что это такое. Попытаемся уяснить себе смысл этого закона при помощи аналогий.

Разбираемся что такое ток и сопротивление

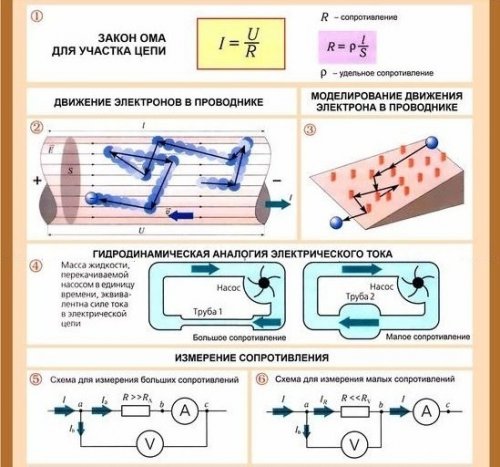
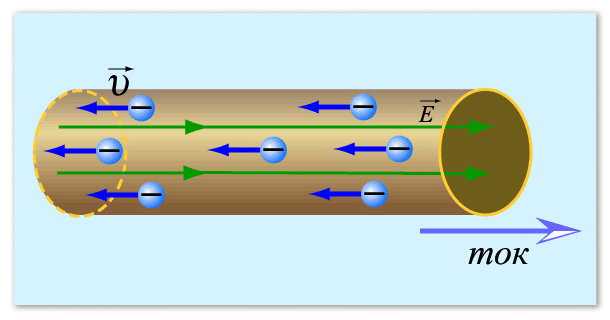
Начнем с понятия электрического тока. Если говорить коротко, электрический ток применительно к металлам — это направленное движение электронов — отрицательно заряженных частиц. Их обычно представляют в виде небольших кружочков. В спокойном состоянии они передвигаются хаотически, постоянно меняя свое направление. При определенных условиях — возникновении разницы потенциалов — эти частицы начинают определенное движение в какую-то сторону. Вот это движение и есть электрический ток.

Чтобы было понятнее, можно сравнить электроны с водой, разлитой на какой-то плоскости. Пока плоскость неподвижна, вода не движется. Но, как только появился наклон (возникла разница потенциалов), вода пришла в движение. С электронами примерно так же.

Примерно так можно себе представить электрический ток

Теперь надо понять, что такое сопротивление и почему с силой тока у них обратная связь: чем выше сопротивление, тем меньше ток. Как известно, электроны движутся по проводнику. Обычно это металлические провода, так как металлы обладают хорошей способностью проводить электрический ток. Мы знаем, что металл имеет плотную кристаллическую решетку: много частиц, которые расположены близко и связаны между собой. Электроны, пробираясь между атомами металла, на них наталкиваются, что затрудняет их движение. Это помогает проиллюстрировать сопротивление, которое оказывает проводник. Вот теперь становится понятным, почему, чем выше сопротивление, тем меньше сила тока — чем больше частиц, тем электронам сложнее преодолевать путь, делают они это медленнее. С этим, вроде, разобрались.

Если у вас есть желание проверить эту зависимость опытным путем, найдите переменный резистор, соедините последовательно резистор — амперметр — источник тока (батарейка). Еще желательно в цепь вставить выключатель — обычный тумблер.

Цепь для проверки зависимости силы тока от сопротивления

Крутя ручку резистора вы изменяете сопротивление. При этом показания на амперметре, который измеряет силу тока, тоже меняются. Причем чем больше сопротивление, тем меньше отклоняется стрелка — меньше ток. Чем сопротивление меньше — тем сильнее отклоняется стрелка — ток больше.

Вместо стрелочного прибора можно использовать цифровой мультиметр в режиме измерения постоянного тока. В этом случае отслеживаются показания на жидкокристаллическом цифровом табло.

Зависимость тока от сопротивления почти линейная, то есть на графике отражается почти прямой линией. Почему почти — об этом надо говорить отдельно, но это другая история.

Говорим о напряжении

Не менее важно понять что такое напряжение. Давайте сразу начнем с аналогии и снова используем воду. Пусть в воронке находится вода. Она просачивается через узкое горлышко, которое создает сопротивление. Если представить, что на воду уложили груз, движение воды ускорится. Этот груз — и есть напряжение. И теперь тоже понятно, почему чем выше напряжение, тем сильнее ток — чем сильнее давление, тем быстрее будет двигаться вода. То есть, зависимость прямая: больше напряжение — больше ток. И именно это положение отражает закон Ома — «давление» стоит в числителе (в верхней части дроби).

Можно попробовать представить напряжение по-другому. Есть все те же электроны, которые скопились на одном краю источника питания. На втором краю их мало. Так как каждый из электронов имеет какой-то заряд, там, где их много, суммарный заряд больше, где мало — меньше. Разница между зарядами и есть напряжение. Это тоже несложно представить. С точки зрения электричества — это более корректное представление, хоть и не точное.

На тему закона Ома есть немало забавных картинок, позволяющих чуть лучше понять все эти явления. Одна из них перед вами и иллюстрирует, как ток зависит от напряжения и сопротивления. Смотрите что получается: сопротивление старается уменьшить ток (обратная зависимость), а с ростом напряжения он увеличивается (прямая зависимость). Это и есть закон Ома, но переданный простыми словами.

Благодаря картинке просто понять зависимость тока от напряжения и сопротивления

Если вы хотите убедиться и в этой зависимости, тоже надо создать простенькую цепь. Но нужен будет либо регулируемый источник питания, либо несколько батареек, которые выдают разное напряжение. Или можно последовательно включать несколько батареек — тоже вариант. Но менять/подпаивать батарейки надо при разорванной цепи (выключенном тумблере).

В этой схеме используются два измерительных прибора: амперметр включается последовательно с нагрузкой (резистор на схеме ниже), вольтметр параллельно нагрузке.

Схема для иллюстрации закона Ома

Так как другие параметры цепи остаются в норме, при увеличении напряжения мы увидим увеличение силы тока. Чем больше напряжение подаем, тем больше отклоняются стрелки вольтметра и амперметра. Если задаться целью построить график, он будет в виде прямой. Если поставить другое сопротивление, график также будет в виде прямой, но угол наклона ее изменится.

Что изменится для полной цепи

В ситуации выше рассмотрен только некоторый участок цепи, обладающий каким-то фиксированным сопротивлением. Мы предполагаем, что при определенных условиях электроны начнут движение. Причина этого движения — тот самый груз на картинке. В реальных условиях это — источник тока. Это может быть батарейка, генератор постоянного тока, подключенный шнур блока питания и т.д. При подключении источника питания к проводнику в нем начинает протекать ток. Это мы тоже знаем и наблюдаем, когда включаем лампу в сеть, ставим заряжаться мобильный телефон и т.д.

Полная цепь включает в себя источник питания

Участок цепи имеет какое-то сопротивление. Это понятно. Но источник питания тоже имеет сопротивление. Его обычно обозначают маленько буквой r. Так как ток бежит по кругу, ему приходится преодолевать сопротивление провода и сопротивление источника тока. Вот это суммарное сопротивление цепи и источника питания — называют импеданс. Говорят еще что это комплексное сопротивление. В формуле Ома для полной цепи его отображают при помощи суммы. В знаменателе стоит сумма сопротивлений цепи и внутреннего сопротивления источника тока (R + r).

Всем, наверное, понятно, что именно источник тока создает нужные условия для движения электронов. Все благодаря тому, что он обладает ЭДС — электродвижущей силой. Эта величина обозначается обычно E. Чем больше эта сила, тем больше ток. Это тоже, вроде, понятно. Поэтому обозначение ЭДС — латинскую букву E — ставят в числитель. Таким образом, формулировка закона Ома для полной цепи звучит так:

Сила тока прямо пропорциональна ЭДС источника тока и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника тока.

Вроде не слишком сложно, но можно попробовать еще проще:

Чем выше ЭДС источника тока, тем больше ток.
Чем больше суммарное сопротивление, тем ток меньше.

Как найти сопротивление, напряжение

Зная формулу закона Ома для участка цепи, мы можем рассчитать напряжение и сопротивление. Напряжение находится как произведение силы тока и сопротивления.

Формула напряжения и сопротивления по закону Ома

Сопротивление можно найти, разделив напряжение на ток. Все действительно несложно. Если мы знаем, что к участку цепи было проложено определенное напряжение и знаем какой при этом был ток, мы можем рассчитать сопротивление. Для этого напряжение делим на ток. Получаем как раз величину сопротивления этого куска цепи.

С другой стороны, если мы знаем сопротивление и силу тока, которая должна быть, мы сможем рассчитать напряжение. Надо всего лишь перемножить силу тока и сопротивление. Это даст напряжение, которое необходимо подать на этот участок цепи чтобы получить требуемый ток.

Параллельное и последовательное соединение

В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.

Закон Ома для параллельного и последовательного соединения

Последовательное соединение

Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.

Последовательное соединение и параметры этого участка цепи

При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.

Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.

Параллельное соединение

Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.

Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.

Законы для параллельного соединения

Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.

Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.

Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.

Что нам дает параллельное и последовательное соединение?

Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:

Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга. Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя. Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.

Практическое применение закона Ома: можно создавать источники питания с нужным напряжением и силой тока

В общем, это наиболее распространенные варианты использования этих соединений.

Источник

Закон Ома

Главная
/
Физика
/
Закон Ома

Чтобы посчитать Закон Ома воспользуйтесь нашим очень удобным онлайн калькулятором:

Закон Ома для участка цепи

Закон Ома для участка цепи гласит, что сила тока (I) на участке электрической цепи прямо пропорциональна напряжению (U) на концах участка цепи и обратно пропорциональна его сопротивлению (R).

Онлайн калькулятор

Найти силу тока

Напряжение: U =В
Сопротивление: R =Ом

Сила тока: I =

Формула

I = ^U/_R

Пример

Если напряжение на концах участка цепи U = 12 В, а его электрическое сопротивление R = 2 Ом, то:

Сила тока на этом участке I = ¹²/₂= 6 А

Найти напряжение

Сила тока: I =A
Сопротивление: R =Ом

Напряжение: U =

Формула

U = I ⋅ R

Пример

Если сила тока на участке цепи I = 6 А, а электрическое сопротивление этого участка R = 2 Ом, то:

Напряжение на этом участке U = 6⋅2 = 12 В

Найти сопротивление

Напряжение: U =В
Сила тока: I =A

Сопротивление: R =

Ом

Формула

R = ^U/_I

Пример

Если напряжение на концах участка цепи U = 12 В, а сила тока на участке цепи I = 6 А, то:

Электрическое сопротивление на этом участке R = ¹²/₆ = 2 Ом

Закон Ома для полной цепи

Закон Ома для полной цепи гласит, что сила тока в цепи пропорциональна действующей в цепи электродвижущей силе (ЭДС) и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.

Онлайн калькулятор

Найти силу тока

ЭДС: ε =В
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =Ом

Сила тока: I =

Формула

I = ^ε/_R+r

Пример

Если ЭДС источника напряжения ε = 12 В, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:

Сила тока I = ¹²/₄₊₂ = 2 А

Найти ЭДС

Сила тока: I =А
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =Ом

ЭДС: ε =

Формула

ε = I ⋅ (R+r)

Пример

Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:

ЭДС ε = 2 ⋅ (4+2) = 12 В

Найти внутреннее сопротивление источника напряжения

Сила тока: I =А
ЭДС: ε =В
Сопротивление всех внешних элементов цепи: R =Ом

Внутреннее сопротивление источника напряжения: r =

Ом

Формула

r = ^ε/_I — R

Пример

Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а ЭДС источника напряжения ε = 12 В, то:

Внутреннее сопротивление источника напряжения r = 12/2 — 4 = 2 Ом

Найти сопротивление всех внешних элементов цепи

Сила тока: I =А
ЭДС: ε =В
Внутреннее сопротивление источника напряжения: r =Ом

Сопротивление всех внешних элементов цепи: R =

Ом

Формула

R = ^ε/_I — r

Пример

Если сила тока в цепи I = 2A, внутреннее сопротивление источника напряжения r = 2 Ом, а ЭДС источника напряжения ε = 12 В, то:

Сопротивление всех внешних элементов цепи: R = 12/2 — 2 = 4 Ом

См. также

Источник

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
Сторонняя сила
Закон Ома для полной цепи
КПД электрической цепи
Закон Ома для неоднородного участка

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд :

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила $vec{F_E}$ , направленная против движения заряда (т.е. против направления тока).

к оглавлению ▴

Сторонняя сила

Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила $vec{F_{CT}}$ не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через $A_{CT}$ работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы $A_{CT}$ называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, $A_{CT}$ — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа $A_{CT}$ прямо пропорциональна перемещаемому заряду . Поэтому отношение $A_{CT}/q$ уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :

$mathcal E = frac{displaystyle A_{CT}}{displaystyle q vphantom{1^a}}.$ (1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

к оглавлению ▴

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь

Наша задача — найти силу тока в цепи и напряжение на резисторе .

За время по цепи проходит заряд q = It . Согласно формуле (1) источник тока совершает при этом работу:

$A_{CT} = Eq = EIt.$ (2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:

(3)

Итак, $A_{CT} = Q$ , и мы приравниваем правые части формул (2) и (3):

После сокращения на получаем:

Вот мы и нашли ток в цепи:

$I = frac{displaystyle mathcal E}{displaystyle R + r vphantom{1^a}}.$ (4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления (R = 0) , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

$I_{K3} = frac{displaystyle mathcal E}{displaystyle r vphantom{1^a}}.$

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:

$U = IR = frac{displaystyle mathcal E R}{displaystyle R + r vphantom{1^a}}.$ (5)

Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При r = 0 формула (5) даёт .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина R + r неотличима от , и формула (5) снова даёт нам .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

к оглавлению ▴

КПД электрической цепи

Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим $Q_{polezn}$ .

Если сила тока в цепи равна , то

$Q_{polezn} = I^2Rt.$

Некоторое количество теплоты выделяется также на источнике тока:

$Q_{ist} = I^2rt.$

Полное количество теплоты, которое выделяется в цепи, равно:

$Q_{poln} = Q_{polezn} + Q_{ist} = I^2Rt + I^2rt = I^2(R + r)t.$

КПД электрической цепи — это отношение полезного тепла к полному:

$eta = frac{displaystyle Q_{polezn}}{displaystyle Q_{poln} vphantom{1^a}} = frac{displaystyle I^2Rt}{displaystyle I^2(R+r)t vphantom{1^a}} = frac{displaystyle R}{displaystyle R+r vphantom{1^a}}.$

КПД цепи равен единице лишь в том случае, если источник тока идеальный (r = 0) .

к оглавлению ▴

Закон Ома для неоднородного участка

Простой закон Ома U = IR справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3 показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно , можно просто заменить резистор на резистор R + r ).

Рис. 3. ЭДС «помогает» току:

Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: . За время через участок проходит заряд q = It , при этом стационарное электрическое поле совершает работу:

$A_{POL} = Uq = UIt.$

Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):

$A_{CT} = mathcal Eq = mathcal EIt.$

Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло: $A_{POL} + A_{CT} = Q$ .

Подставляем сюда выражения для $A_{POL}$ , $A_{CT}$ и закон Джоуля–Ленца:

Сокращая на , получаем закон Ома для неоднородного участка цепи:

(6)

или, что то же самое:

(7)

Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то . Тогда из формулы (6) получаем U = IR — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на R + r :

Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

$A_{CT} = mathcal E q = mathcal EIt.$

Тогда закон Ома для неоднородного участка примет вид:

(8)

или:

где по-прежнему — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Повторим основные понятия и определения по теме «Закон Ома».

Напомним, что напряжение измеряется в вольтах.

Сила тока измеряется в амперах.

Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.

Основные определения, которые мы используем в решении задач:

Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.

Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.

Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.

Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.

По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).

Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.

Сопротивление измеряют в омах (Ом).

Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).

Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:

Сопротивление проводника тем больше, чем больше его длина.
Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.

Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм²/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:

Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.

Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм² от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм²/м.

Решение:

Из закона Ома для проводника или участка цепи без источника следует:

$displaystyle I=frac{U}{R};$

$displaystyle R=frac{U}{I}.$

По графику: при

Из формулы сопротивления выражаем и находим длину проводника:

Ответ: 10.

Задача 2. Через поперечное сечение проводников за 8 с прошло 10²⁰ электронов. Какова сила тока в проводнике? Ответ дайте в амперах.

Решение:

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Заряд всех электронов: где е — модуль заряда электрона, $e=1,6cdot 10^{-19}$ Кл.

Тогда $displaystyle I=frac{Ncdot e}{t}=frac{10^{20}cdot 1,6cdot 10^{-19}}{8}=2 A.$

Ответ: 2.

Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)

Решение:

По закону Ома для полной цепи:

Тогда $displaystyle I=frac{5}{66+4}=0,07 A.$

Ответ: 0,07.

Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.

Решение:

Сила тока короткого замыкания определяется следующим образом:

Отсюда выражаем и находим внутреннее сопротивление источника:

При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:

Отсюда выражаем сопротивление резистора и находим его:

Ответ: 1,9.

Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.

Решение:

Выражаем время в секундах: t = 10 минут = 600 с.

Определяем силу тока по закону Ома для полной цепи:

Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Отсюда Кл.

Ответ: 1500.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Закон Ома для участка цепи и полной цепи: формулы и определения

Закон Ома для участка цепи:

Определение единицы сопротивления — Ом

Закон Ома для полной цепи

Как запомнить формулы закона Ома

Закон Ома для участка цепи

Закон Ома для участка цепи: формула. Зависимость силы тока от напряжения

Электрическая цепь и закон Ома

«Треугольник Ома»

Калькулятор, который основан на законе Ома

3. Последовательное и параллельное соединение проводников

Последовательное соединение

Как звучит закон Ома для участка цепи

Разбираемся что такое ток и сопротивление

Говорим о напряжении

Что изменится для полной цепи

Как найти сопротивление, напряжение

Параллельное и последовательное соединение

Последовательное соединение

Параллельное соединение

Что нам дает параллельное и последовательное соединение?

Закон Ома

Закон Ома для участка цепи

Онлайн калькулятор

Найти силу тока

Формула

Пример

Найти напряжение

Формула

Пример

Найти сопротивление

Формула

Пример

Закон Ома для полной цепи

Онлайн калькулятор

Найти силу тока

Формула

Пример

Найти ЭДС

Формула

Пример

Найти внутреннее сопротивление источника напряжения

Формула

Пример

Найти сопротивление всех внешних элементов цепи

Формула

Пример

См. также

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

Сторонняя сила

Закон Ома для полной цепи

КПД электрической цепи

Закон Ома для неоднородного участка

Не пропустите также: