Речь в статье пойдет о КПД различных циклов, проводимых с газом. При этом давайте помнить, что внутренняя энергия изменяется тогда, когда изменяется температура, а в адиабатном процессе передачи тепла не происходит, то есть для совершения работы в таком процессе газ «изыскивает внутренние резервы». Кроме того, работа численно равна площади под кривой процесса, а работа за цикл — площади внутри цикла.
Задача 1.
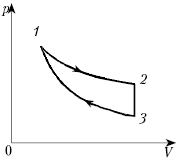
На рисунке представлена диаграмма цикла с одноатомным идеальным газом. Участки и
— адиабаты. Вычислите КПД
данной тепловой машины и максимально возможный КПД
.
К задаче 1
КПД тепловой машины можно вычислить как
Машина получает тепло только на участке AB, и, так как работы здесь не совершается, то можно вычислить количество теплоты, полученное газом, как увеличение его внутренней энергии:
Работа численно равна площади, ограниченной циклом. Поэтому
Участк и
по условию – адиабаты, то есть передачи тепла газу на этих участках не происходит, следовательно, работа будет совершена за счет «внутренних резервов» — то есть внутренней энергии. Нужно, следовательно, найти, как она изменилась.
Задачу можно решить двумя способами. Во-первых, просто определить температуры в точках и
,
и
, это легко сделать из данных графика с помощью уравнения Менделеева-Клапейрона, и затем посчитать
. Но, так как
, а
,то изменение внутренней энергии будет равно
Определим максимальный КПД. Посчитаем его как КПД цикла Карно. Максимальная температура газа будет достигнута в точке , а минимальная – в точке
:
Ответ: ,
.
Задача 2.
Над идеальным одноатомным газом проводят цикл, включающий изобару, изохору, изотерму, при этом работа газа за цикл равна кДж. В процессе изотермического сжатия (3-1) внешние силы совершают над газом положительную работу
кДж. Найдите КПД данной тепловой машины.
К задаче 2
Работа газа в процессе 1-2– площадь под линией процесса 1-2. Работа внешних сил – площадь под циклом (под линией 3-1). Поэтому полная работа за цикл – это разность работы газа и работы внешних сил, площадь, ограниченная линиями цикла. Она будет равна 5 кДж.
Работа газа в процессе 1-2, таким образом, равна 8 кДж. А поскольку процесс изобарный, то кДж. Тогда КПД
Ответ: .
Задача 3.
КПД тепловой машины, работающей по циклу, включающему изотермический (1-2) и адиабатный (3-1) процессы, равен , причем работа, совершенная 2 моль одноатомного идеального газа в изотермическом процессе
кДж. Найдите разность
максимальной и минимальной температур газа в цикле.
К задаче 3
Полная площадь под кривой процесса 1-2 равна кДж. При этом, так как КПД машины 25%, то площадь внутри цикла равна
, а под кривой 3-1 —
. В процессе 1-2 изменения внутренней энергии не было, так как температура не менялась, а в процессе 3-1 газу не передавали тепло, следовательно, работа совершена за счет внутренней энергии. Т.е.
Ответ: 500 K.
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505

Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
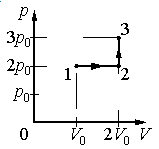
Задание EF17966
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.1k
Первый закон термодинамики.
Аналитическое
выражение I
закона т/д-ки.
Если к 1кг рабочего
тела подвести некоторое элементарное
количество теплоты dQ,
то его температура изменится на величину
dT,
а внутренняя энергия на dU.
При изменении температуры, объем
увеличится на величину dV,
а с увеличением объема увеличивается
его потенциальная энергия и будет
совершена внешняя работа расширения
dL.
И если в рабочем теле не происходит
каких-либо других явлений и отсутствует
кинетическая энергия видимого движения,
то согласно закону сохранения энергии
можно записать:
dq=dU+dl;
q=ΔU+l;
ΔU=q-l;
U2-U1=q-l.
(23)
Энергия, подведенная
в форме теплоты к рабочему телу расходуется
на изменение внутренней энергии ΔU
и на совершение работы расширения (l).
Внутренняя
энергия.
Внутренняя энергия
включает в себя:
1 кинетическую
энергию поступательного,
вращательного и колебательного движения
частиц.
2 потенциальную
энергию взаимодействия частиц.
3 энергию электронных
оболочек.
4 внутриядерную
энергию.
Т.к. в большинстве
случаев 3 и 4 являются постоянными, то в
дальнейшем под внутренней энергией
будем понимать энергию хаотического
движения молекул и атомов. Для реальных
газов необходимо учитывать потенциальную
энергию. Поэтому внутренняя энергия
есть некоторая однозначная функция
состояния тела, т.е. любых двух независимых
параметров.
U=f(P,T);
U=f(υ,P);
U=
f(υ,T).
Изменение внутренней
энергии не зависит от характера процесса,
а определяет только начальное и конечное
состояние тела.
(24)
Внутренняя
энергия идеального газа, в которой
отсутствуют силы межмолекулярного
взаимодействия не зависит от V
тела или Р, а определяется только конечной
температурой
ΔU=f(T).
(25)
А для реального
нужно учитывать все силы.
Для идеального
газа
Рис. 3.
Изменение внутренней энергии идеального
газа.
ΔU=U2-U1=
U21-U11=
U2’-U1’
(26)
ΔU=f(T2)-f(T1)
(27).
Работа газа. Рабочая диаграмма p-V. Работа расширения и полезная работа газа.
Передача энергии
от одного тела к другому, связанная с
изменением объема рабочего тела, с
перемещением его во внешнем пространстве
или с изменением его положения называется
работой. В этом процессе участвуют два
или более тел. 1-ое тело, производящее
работу – отдает энергию; 2– ое тело
получает энергию. Совершенная газом
работа зависит от p,
V,
T.
Рассмотрим частный
случай: работа расширения 1кг газа в
равновесном процессе при постоянном
давлении. Давление рабочего тела равно
давлению окружающей среды.
Pdf
– сила, действующая на поршень
Элементарная
работа
Работа dl=p·df·dS
(28).
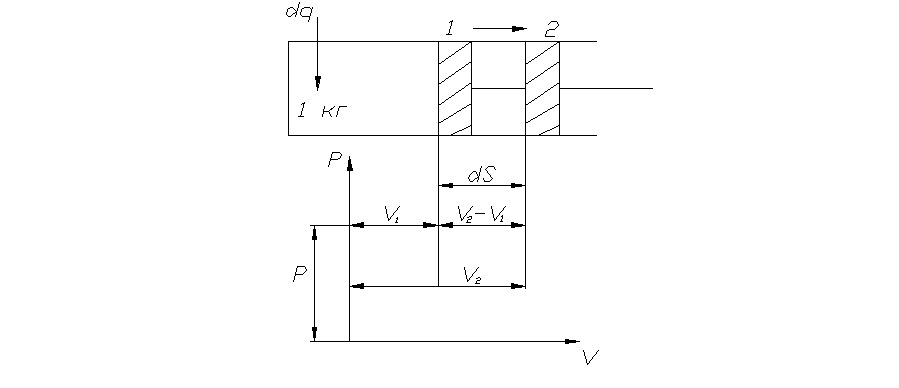
Рис. 4.
Работа l,
совершаемая системой при конечном
изменении объема
от V1
до V2
в произвольном равновесном процессе.
В реальном
произвольном процессе р≠const
и изменяется с
изменением удельного
объема υ, т.е. является функцией объема
p=f(υ)
Рисунок
5. Рисунок
6.
Из рисунка 5 видно,
что S1,2,3,4
под процессом 1- 2 = работе расширения l,
что следует из уравнения 30. Графическое
представление процесса в координатах
p-υ
называется рабочей
диаграммой (рис.5).
Если процесс
осуществляется в направлении 1→2, это
работа расширения, она положительна,
т.к. dυ>0,
совершается самой системой и оценивается
площадью 1234.под линией процесса
12
dv>0
“+ l
” (1234).
Если наоборот,
процесс протекает в направлении 21,
то dυ<0,
работа отрицательна (работа сжатия),
затрачивается извне и оценивается
площадью 4321под линией процесса
21
dv<0
“-l
” (4321).
Работа в отличие
от изменения внутренней энергии зависит
от характера процесса. Рассмотрим 3
процесса совершения работы по а,в и с
(Рис.6). Они начинаются состоянием
1(р1,v1,т1)
и заканчиваются состоянием 2 (р2,v2,т2),
но промежуточные состояния различны.
Изменение внутренней энергии для всех
3 процессов одинаково
ΔU
= ΔUA=
ΔUВ=
ΔUС,
А работа различна
LА>
LВ>
LС.
Встречаются
случаи, когда в рабочем теле изменяется
внешняя кинетическая энергия без
изменения объема (например, перемешиание
мешалками). В таком процессе
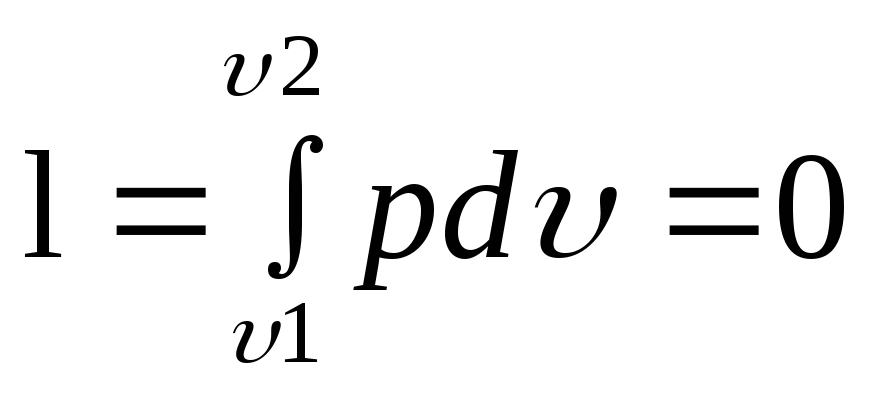
т.к.
( 31)
Работу внешнего
источника обозначим
,
следовательно, работа системы складывается
в общем случае из работы расширения и
работы, совершаемой без изменения
объема:
.
(32)
Полезная
(располагаемая) работа.
При расширении газа не вся работа может
быть полезно использована. Часть этой
работы тратится на вытеснение среды,
давление которой изменяется от р1
до р2..
(33)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Спецвыпуск
Г. А.
Белуха
Работа газа в термодинамике
··· Орловский выпуск ···
Г.А.БЕЛУХА,
школа № 4, г. Ливны, Орловская обл.
Работа газа в термодинамике
Методические рекомендации по
изучению темы, 10-й класс
При изучении работы газа в
термодинамике учащиеся неизбежно сталкиваются с
трудностями, обусловленными слабыми навыками
вычисления работы переменной силы. Поэтому к
восприятию этой темы необходимо готовиться,
начиная уже с изучения работы в механике и решая
с этой целью задачи на работу переменной силы
путём суммирования элементарных работ на всём
пути с помощью интегрирования.
Например, при вычислениях работы силы
Архимеда, силы упругости, силы всемирного
тяготения и т.п. надо учиться суммировать
элементарные величины с помощью простейших
дифференциальных соотношений типа dA = Fds.
Опыт показывает, что старшеклассники легко
справляются с этой задачей, – дугу траектории, на
которой сила увеличивается или уменьшается,
нужно разбить на такие промежутки ds, на
которых силу F можно считать постоянной
величиной, а затем, зная зависимость F = F(s),
подставить её под знак интеграла. Например,
Работа этих сил вычисляется с помощью
простейшего табличного интеграла
Такая методика облегчает адаптацию
будущих студентов к восприятию курса физики в
вузе и устраняет методические сложности,
связанные с умением находить работу переменной
силы в термодинамике и др.
После того как учащиеся усвоили, что
такое внутренняя энергия и как найти её
изменение, целесообразно дать обобщающую схему:
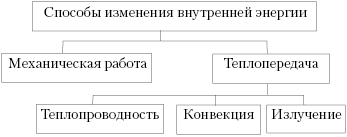
Усвоив, что работа – это один из
способов изменения внутренней энергии,
десятиклассники легко рассчитывают работу газа
в изобарном процессе. На данном этапе необходимо
подчеркнуть, что сила давления газа на всём пути
не меняется, и по третьему закону Ньютона |F2| = |F1|,
знак работы находим из формулы A = Fs cos. Если
= 0°, то A > 0,
если = 180°,
то A < 0. На графике зависимости р(V)
работа численно равна площади под графиком.
Пусть газ расширяется или сжимается
изотермически. Например, газ сжимается под
поршнем, давление изменяется, и в любой момент
времени
При бесконечно малом перемещении
поршня на dl мы получим бесконечно малое
изменение объёма dV, а давление р можно
считать постоянным. По аналогии с нахождением
механической работы переменной силы, составим
простейшее дифференциальное соотношение dA = pdV,
тогда 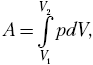
зависимость р (V), запишем 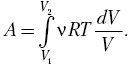
типа 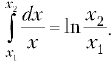
газа в этом случае отрицательна, т.к. = 180°:
т.к. V2 < V1.
Полученную формулу можно переписать,
используя соотношение
Для закрепления решим задачи.
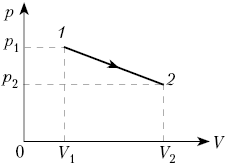
1. Газ переходит из состояния 1
(объём V1, давление р1) в
состояние 2 (объём V2, давление р2)
в процессе, при котором его давление зависит от
объёма линейно. Найдите работу газа.
Решение. Построим примерный
график зависимости p от V. Работа равна
площади под графиком, т.е. площади трапеции:
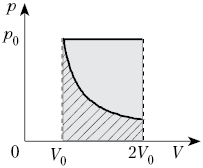
2. Один моль воздуха, находящийся при
нормальных условиях, расширяется от объёма V0
до 2V0 двумя способами – изотермически
и изобарно. Сравните работу, совершённую
воздухом в этих процессах.
Решение
При изобарном процессе Ap = р0V, но р0 =
RT0/V0,
V = V0,
следовательно, Ap = RT0.
При изотермическом процессе:
Сравним:
Изучив первый закон термодинамики и
его применение к изопроцессам и закрепив
решением задач тему о работе в термодинамике,
учащиеся подготовились к восприятию наиболее
сложной части термодинамики «Работа циклов и КПД
тепловых машин». Этот материал я излагаю в
следующей последовательности: работа циклов –
цикл Карно – КПД тепловых машин – круговые
процессы.
процессом (или циклом) называется
термодинамический процесс, в результате
которого тело, пройдя ряд состояний,
возвращается в исходное состояние. Если все
процессы в цикле равновесные, то цикл считается
равновесным. Его можно изобразить графически в
виде замкнутой кривой.
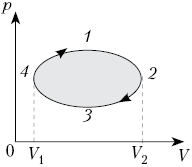
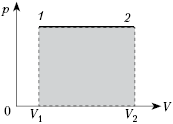
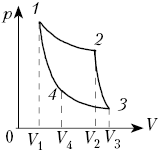
На рисунке показан график зависимости
давления p от объёма V (диаграмма p, V)
для некоторого цикла 1–2–3–4–1. На участках 1–2
и 4–1 газ расширяется и совершает
положительную работу А1, численно
равную площади фигуры V1412V2.
На участке 2–3–4 газ сжимается и совершает
работу А2, модуль которой равен
площади фигуры V2234V1. Полная
работа газ за цикл А = А1 + А2,
т.е. положительна и равна площади фигуры 12341.
Если равновесный цикл изображается
замкнутой кривой на р, V-диаграмме,
которая обходится по часовой стрелке, то работа
тела положительна, а цикл накзывается прямым.
Если замкнутая кривая на р, V-диаграмме
обходится против часовой стрелки, то газ
совершает отрицательную работу за цикл, а цикл
называется обратным. В любом случае модуль
работы газа за цикл равен площади фигуры,
ограниченной графиком цикла на р, V-диаграмме.
В круговом процессе рабочее тело
возвращается в исходное состояние, т.е. в
состояние с первоначальной внутренней энергией.
Это значит, что изменение внутренней энергии за
цикл равно нулю: U = 0.
Так как, по первому закону термодинамики, для
всего цикла Q = U + A, то Q = A.
Итак, алгебраическая сумма всех количеств
теплоты, полученных за цикл, равна работе тела за
цикл: Aц = Qн + Qх = Qн
– |Qх|.
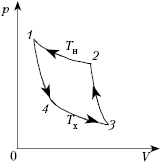
Рассмотрим один из круговых процессов
– цикл Карно. Он состоит из двух изотермических и
двух адиабатических процессов. Пусть рабочим
телом является идеальный газ. Тогда на участке 1–2
изотермического расширения, согласно первому
закону термодинамики, всё получаемое газом тепло
идёт на совершение положительной работы: Q12 = A12.
То есть нет никаких потерь тепла в окружающее
пространство и никакого изменения внутренней
энергии: U = 0,
т.к. T12 = const (потому что газ –
идеальный).
На участке 2–3 адиабатного
расширения газ совершает положительную работу
за счёт изменения внутренней энергии, т.к. Qад = 0
= U23 + Aг23
Aг23 = –
U23.
Здесь также нет потерь тепла, по определению
адиабатного процесса.
На участке 3–4 над газом
совершается положительная работа внешней силой,
но он не нагревается (изотермический процесс).
Благодаря достаточно медленно протекающему
процессу и хорошему контакту с холодильником газ
успевает отдавать получаемую за счёт работы
энергию в виде тепла холодильнику. Сам же газ
совершает при этом отрицательную работу: Q34 = Aг34
< 0.
На участке 4–1 газ адиабатно (без
теплообмена) сжимается до исходного состояния.
При этом он совершает отрицательную работу, а
внешние силы – положительную: 0 = U41 + Aг41
Aг41 = –
U41.
Таким образом, за цикл газ получает
тепло только на участке 1–2, изотермически
расширяясь:
Холодильнику тепло отдаётся только
при изотермическом сжатии газа на участке 3–4:
Согласно первому закону термодинамики
Aц = Qн – |Qx|;
поэтому
КПД машины, работающей по циклу Карно,
найдём по формуле
Согласно закону Бойля–Мариотта для
процессов 1–2 и 3–4, а также уравнению
Пуассона для процессов 2–3 и 4–1, легко
доказать, что
(Хорошо бы увидеть, как автор это
делает: ведь уравнение Пуассона для диабаты
идеального газа надо ещё получить. – Ред.)
После сокращений получим формулу КПД
тепловой машины, работающей по циклу Карно:
обратному циклу, методически правильно, как
показывает опыт, изучать на примере работы
обратного цикла Карно, т.к. он обратим и его можно
провести в обратном направлении: расширять газ
при понижении температуры от Tн до Tx
(процесс 1–4) и при низкой температуре Tx
(процесс 4–3), а затем сжимать (процессы 3–2
и 2–1). Теперь двигатель совершает работу,
чтобы привести в действие холодильную машину.
Рабочее тело отнимает количество теплоты Qx
у продуктов внутри при низкой температуре Tх,
а отдаёт количество теплоты Qн
окружающим телам, за пределами холодильника, при
более высокой температуре Tн. Таким
образом, машина, работающая по обратному циклу
Карно, уже не тепловая, а идеальная холодильная.
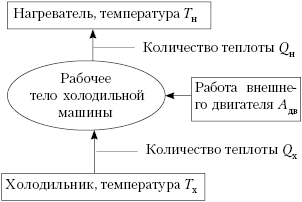
Роль нагревателя (отдающего тепло) выполняет
тело с более низкой температурой. Но, сохранив
названия элементов, как в тепловой машине,
работающей по прямому циклу, мы можем
представить блок-схему холодильника в следующем
виде:
Обратим внимание, что тепло от
холодного тела переходит в холодильной машине к
телу с более высокой температурой не
самопроизвольно, а за счёт работы внешней силы.
Важнейшей характеристикой
холодильника является холодильный коэффициент , определяющий
эффективность работы холодильника и равный
отношению количества теплоты, отнятого от
холодильной камеры Qх к затраченной
энергии внешнего источника
За один обратный цикл рабочее тело
получает от холодильника количество теплоты Qх
и отдаёт в окружающее пространство количество
теплоты Qн, что больше Qх на
работу Aдв, совершаемую
электродвигателем над газом за цикл: |Qн| = |Qх| + Адв.
Энергия, затраченная двигателем
(электроэнергия в случае компрессорных
электрических холодильников), идёт на полезную
работу над газом, а также на потери при
нагревании обмоток двигателя электрическим
током QR и на трение в схеме Атр.
Если пренебречь потерями на трение и
джоулево тепло в обмотках двигателя, то
холодильный коэффициент
Учитывая, что в прямом цикле
после несложных преобразований
получим:
Последнее соотношение между
холодильным коэффициентом и КПД тепловой машины,
которая может работать и по обратному циклу,
показывает, что холодильный коэффициент может
быть больше единицы. В этом случае тепла
отнимается от холодильной камеры и возвращается
в комнату больше, чем для этого используется
энергии двигателем.
В случае идеальной тепловой машины,
работающей по обратному циклу Карно (идеального
холодильника), холодильный коэффициент имеет
максимальное значение:
В реальных холодильниках т.к. не вся получаемая
двигателем энергия идёт на работу над рабочим
телом, о чём написано выше.
Решим задачу:
• Оцените стоимость изготовления 1 кг
льда в домашнем холодильнике, если температура
испарения фреона –tх °С,
температура радиатора tн °С.
Стоимость одного киловатт-часа электроэнергии
равна Ц. Температура в комнате t.
Дано:
m, c, t, tн, tх,
, Ц.
____________
Д – ?
Решение
Стоимость Д изготовления льда равна
произведению работы электродвигателя на тариф Ц:
Д = ЦА.
Для превращения воды в лёд с
температурой 0 °С необходимо отвести от неё
количество теплоты Q = m(ct + ). Считаем
приближённо, что над фреоном совершается
обратный цикл Карно с изотермами при
температурах Tн и Tх.
Используем формулы для холодильного
коэффициента: по определению, = Q/A и для
идеального холодильника ид = Tх/(Tн – Tх).
Из условия следует, что
ид.
Решаем совместно три последних
уравнения:
Разбирая с учащимися эту задачу,
необходимо обратить внимание на то, что основная
работа холодильного устройства идёт не на
охлаждение продуктов, а на поддержание
температуры внутри холодильного шкафа путём
периодической откачки тепла, проникающего
сквозь стенки холодильника.
Для закрепления темы можно решить
задачу:
• КПД тепловой машины, работающей по
циклу, состоящему из изотермического процесса 1–2,
изохорического 2–3 и адиабатического 3–1,
равен , а
разность максимальной и минимальной температур
газа в цикле равна T. Найдите работу, совершённую
моль одноатомного
идеального газа в изотермическом процессе.
Решение
При решении задач, в которых
фигурирует КПД цикла, полезно предварительно
проанализировать все участки цикла, используя
первый закон термодинамики, и выявить участки,
где тело получает и отдаёт тепло. Проведём
мысленно ряд изотерм на р, V-диаграмме.
Тогда станет ясно, что максимальная температура
в цикле на изотерме, а минимальная – в т. 3.
Обозначим их через T1 и T3
соответственно.
На участке 1–2 изменение
внутренней энергии идеального газа U2 – U1 = 0.
По первому закону термодинамики, Q12 = (U2 – U1) + А12.
Так как на участке 1–2 газ расширялся, то
работа газа А12 > 0. Значит, и
подведённое к газу количество теплоты на этом
участке Q12 > 0, причём Q12 = А12.
На участке 2–3 работа газа равна
нулю. Поэтому Q23 = U3 – U2.
Воспользовавшись выражениями U2=
cVT1
и тем, что T1 – T3 = T, получим Q23 = –
cV
T < 0.
Это означает, что на участке 2–3 газ получает
отрицательное количество теплоты, т.е. отдаёт
тепло.
На участке 3–1 теплообмена нет,
т.е. Q31 = 0 и, по первому закону
термодинамики, 0 = (U1 – U3) + A31.
Тогда работа газа
A31 = U3 – U1 = cV(T3 –T1) = –
cV
T.
Итак, за цикл газ совершил работу A12 + А31 = А12 – cV
T и получил
тепло только на участке 1–2. КПД цикла
Так как то работа газа на изотерме равна
Геннадий Антонович Белуха –
заслуженный учитель РФ, педагогический стаж 20
лет, ежегодно его ученики занимают призовые
места на различных этапах всероссийской
олимпиады по физике. Хобби – компьютерная
техника.
Работа идеального газа
Рассмотрим газ, который находится в цилиндре, закрытом поршнем (рис.1).
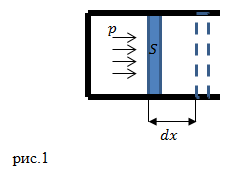
Пусть газ при расширении передвинет поршень на малое расстояние . Таким образом, газ выполнит работу над поршнем (
):
где F – сила, с которой газ действует на поршень, S – площадь поршня; p – давление газа на поршень; – изменение объёма газа под поршнем. Результирующая работа газа, если его объем изменяется от
до
находится как:
Более конкретный результат интегрирования определяет зависимость . Формула (2) для вычисления работы справедлива для изменения объема всех видов тел (газа, жидкости и твердого тела).
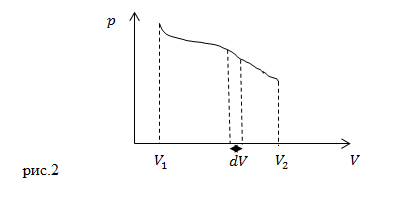
Часто работу газа изображают при помощи графиков в осях (рис.2). Если объем газа увеличивается на
, то работа газа (
) – это площадь криволинейной трапеции с основанием
на рис. 2. Суммарная работа, которую совершил газ, изменяя объем от
до
, определена площадью, которая ограничивается осью абсцисс, кривой
и прямыми
и
.
Работа идеального газа для отдельных процессов
В изобарном процессе () работа вычисляется при помощи формулы:
В изохорном процессе работа газа равна нулю, так как изменения объема не происходит:
Найдем работу для изотермического процесса ():
где из уравнения Менделеева – Клапейрона: – молярная масса газа; m – масса газа). Получили, что для изотермического процесса работа равна:
Для адиабатного процесса, который проходит без обмена теплом окружающей среды и газа работу проще найти из первого начала термодинамики:
Так как то получаем, что в адиабатном процессе газ выполняется работу за счет уменьшения внутренней энергии:
где i – число степеней свободы молекулы газа.









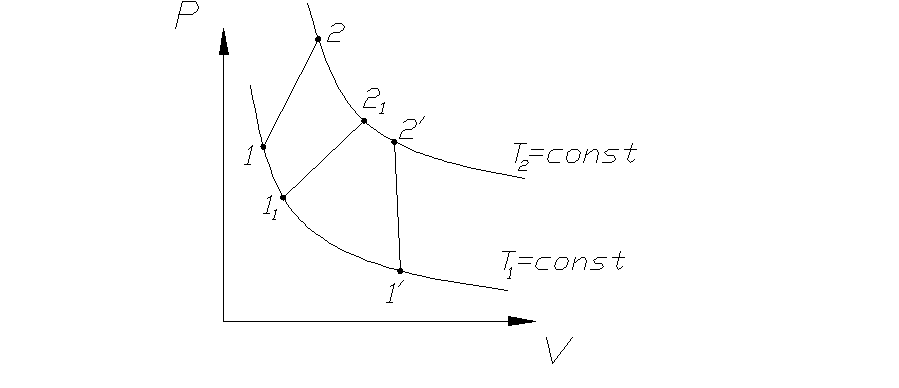
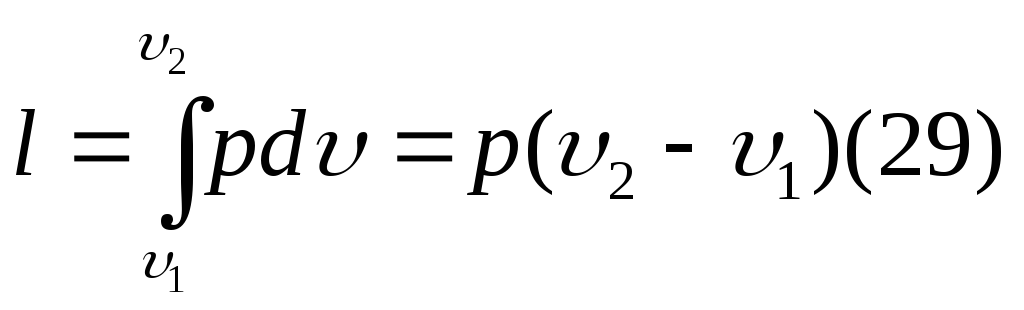
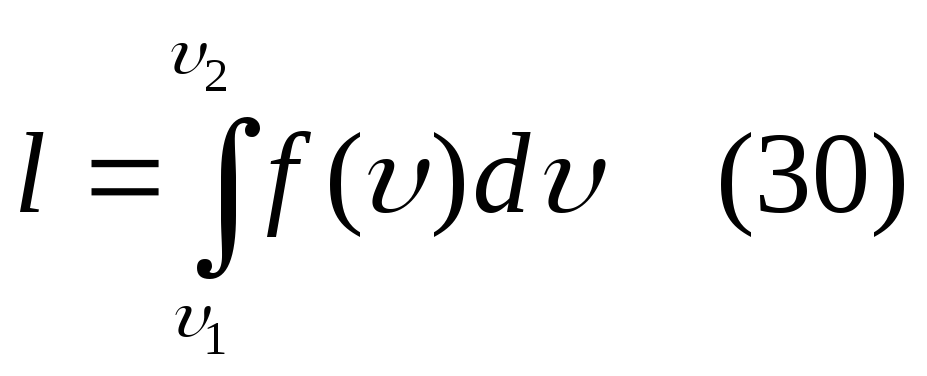
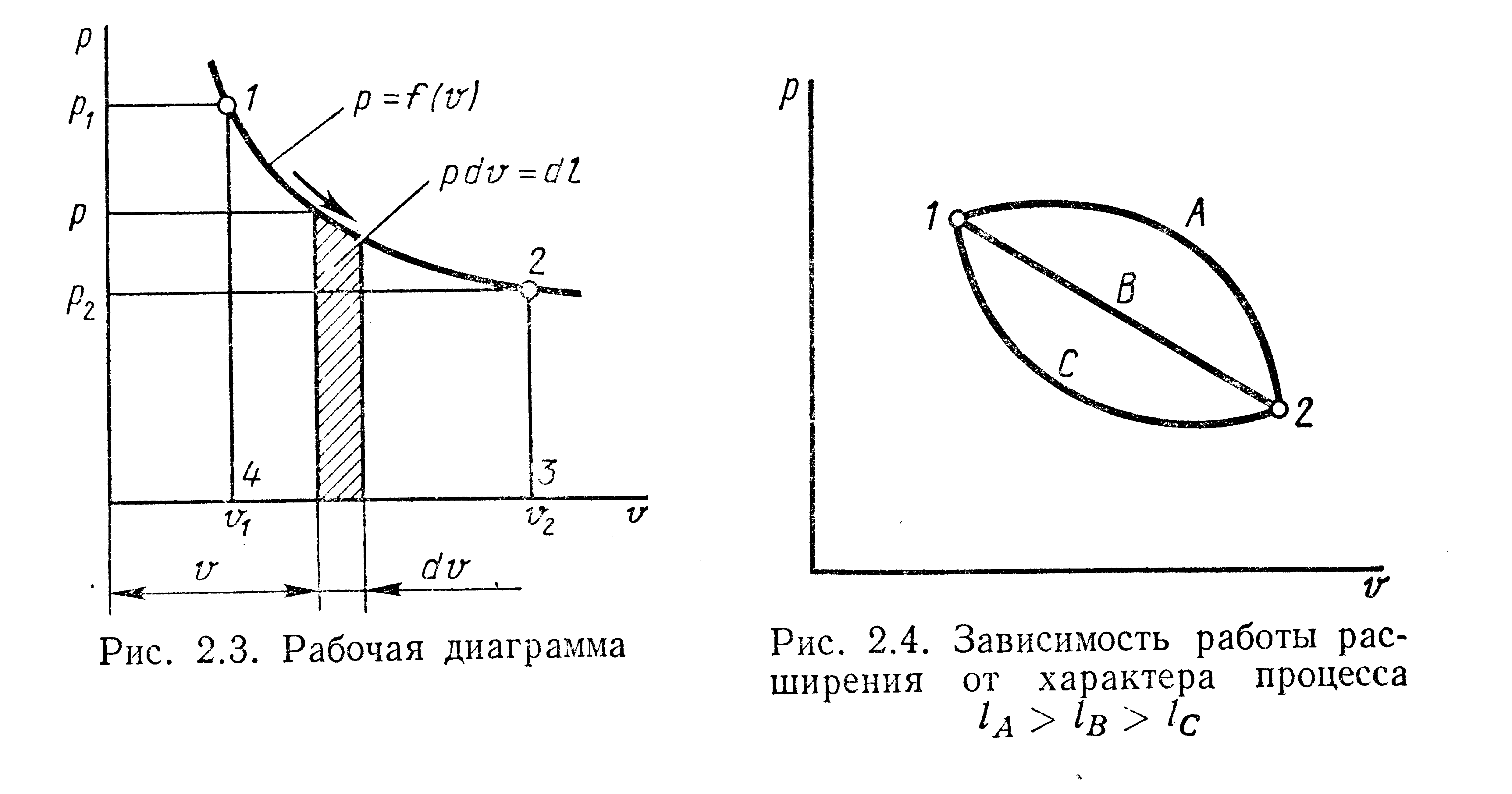
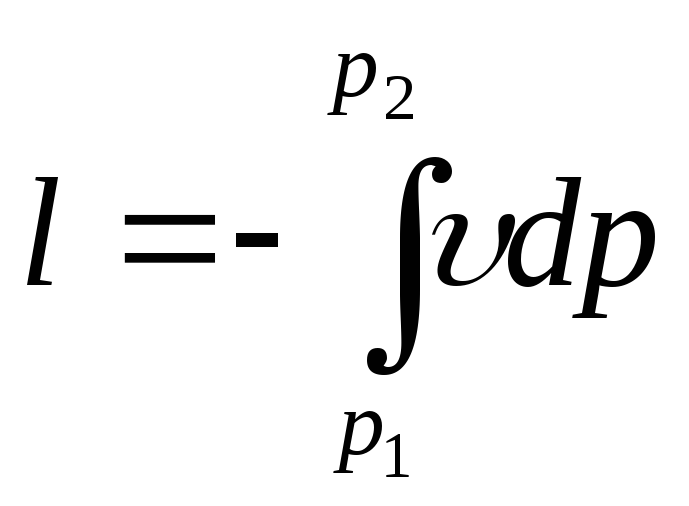
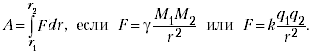
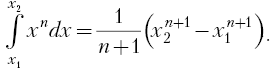
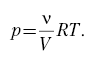
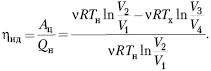
![Rendered by QuickLaTeX.com [A=int^{V_2}_{V_1}{pdV} qquad (2)]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-307146ee2b5ca3587ed0509196a22027_l3.png)
![Rendered by QuickLaTeX.com [A_{p=const}=pint^{V_2}_{V_1}{dV=pleft(V_2-V_1right)} qquad (3)]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fe5676918253ce4d339056f88171b922_l3.png)