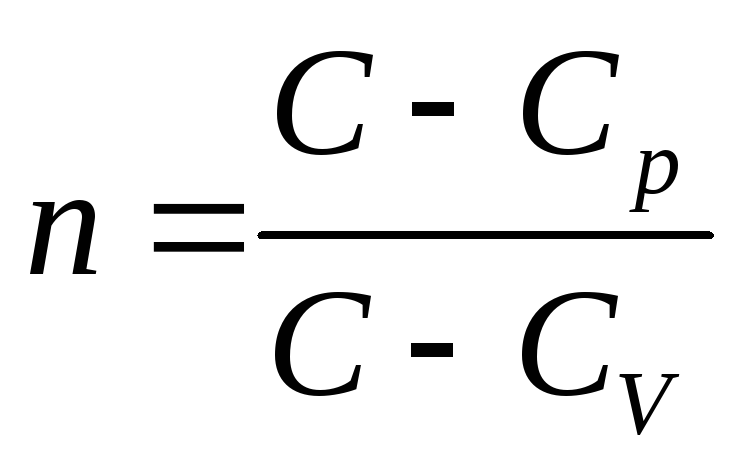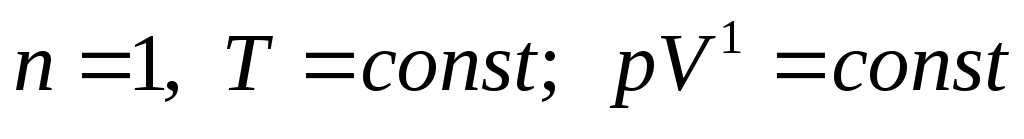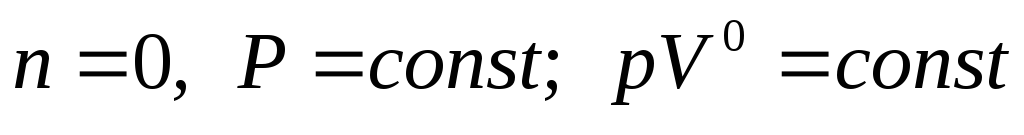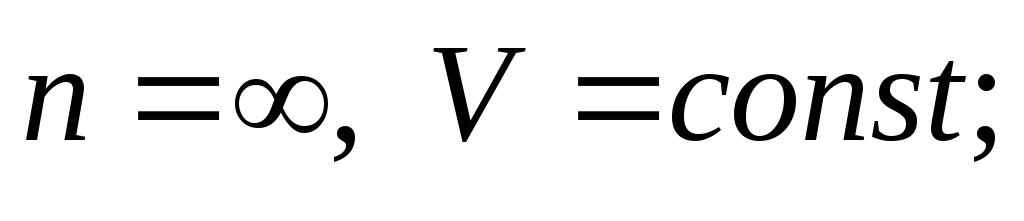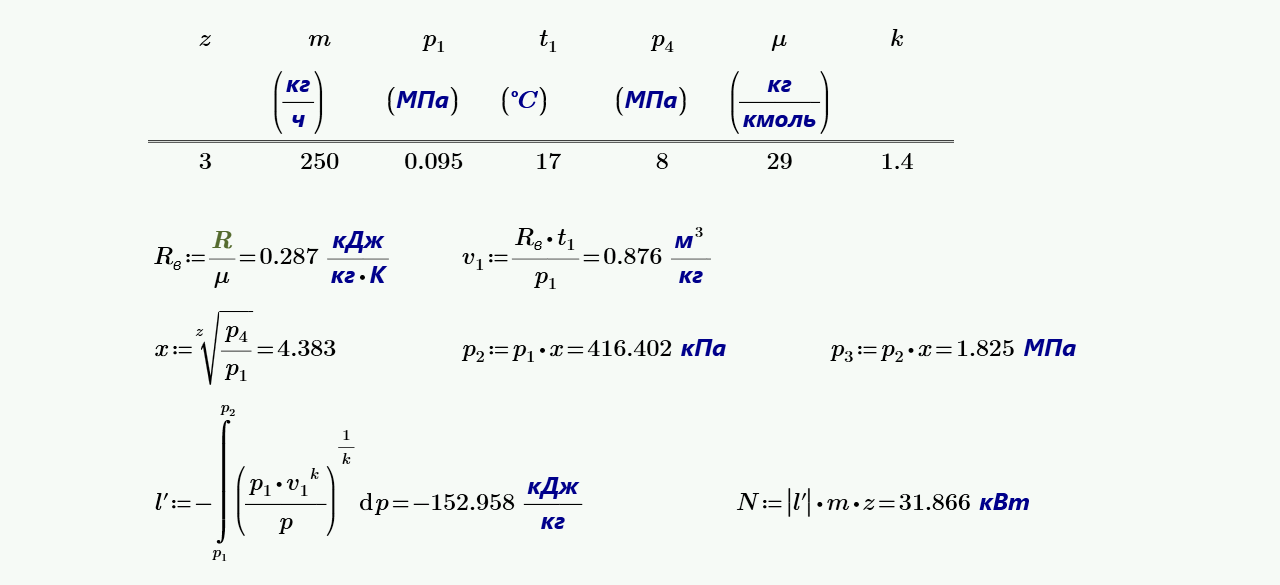Как найти показатель политропы для воздуха

Политропные процессы

Уравнение политропного процесса. Политропными называют процессы, протекающие при постоянной теплоемкости: с = const.

Выше были рассмотрены простейшие процессы, в которых один из параметров состояния (р, v, Т и л) оставался постоянным. В общем же случае при процессах, протекающих в тепловых двигателях с подводом или отводом теплоты, изменяются все параметры состояния.

Выведем уравнение для такого общего процесса, воспользовавшись уравнением первого закона термодинамики в виде

или

Подставляя в это уравнение значение dT из продифференцированного уравнения состояния, получаем

После приведения подобных с учетом уравнения Майера (1.27) получим

Разделив обе части полученного равенства на (с — с_г.) pv и обозначив

После интегрирования и потенцирования получим

Уравнение (2.18а) является искомым уравнением общего термодинамического процесса, называемого политропным. Величину п в этом уравнении называют показателем политропы.

Таким образом, политропным называют процесс с произвольным подводом или отводом теплоты, подчиняющийся уравнению pv n = const.

Политропных процессов может быть бесконечное множество, и у каждого будет свое значение п. Оно может быть произвольным в пределах -оо , но постоянным в рассматриваемом процессе.

(dv 0; dT > 0. Теплота dq = Tds > 0, работа dl = pdv > 0, внутренняя энергия du = c_vdT> 0; c > 0.

II группа политроп: 1 0; dp 0. Теплота dq = TdS > 0, работа dl = pdv > 0, внутренняя энергия газа du = c_vdT > 0. Так

как dq > 0, и dT > 0, то с = k, dv > 0; dp 0, внутренняя энергия du = c_vdT 0.

Схемы преобразования энергии в рассмотренных политропных процессах расширения показаны на рис. 2.8. В процессах сжатия знаки составляющих и направление преобразования энергии изменяются в обратном направлении. Если задан показатель политропы, то может быть найдено процентное соотношение между составляющими энергетического баланса.

Рис. 2.8. Схемы трансформации энергии в политропных процессах

Рассмотрим примеры процессов расширения воздуха при показателях политропы п_Л = 0,6; п₂ = 1,2; и₃= 1,6.

Для воздуха показатель адиабаты !г =1,4.

Доля участвующей в процессе теплоты, идущая на изменение вну тренней энергии, рассчитывается как

Подставляем вычисленные значения в формулу первого начата термодинамики, представив ее в виде следующих отношений:

Тогда для процесса с п_х = 0,6 получаем баланс энергии в виде 1 = 0,5 + 0,5, т.е. теплота, подводимая к рабочему телу, на 50% преобразуется в работу тела над средой, а на 50% — в увеличение внутренней энергии тела.

При п₂ = 1,2 получаем 1 = -1 + 2, т.е. работа тела над средой на 1/2, т.е. на 50%, производится за счет подводимой к телу теплоты и па 50% — за счет уменьшения внутренней энергии тела.

При п₃ = 1,6 получаем 1 = 3-2, т.е. внутренняя энергия тела уменьшается на 1/3 за счет отвода теплоты, а на 2/3 — за счет производства телом работы над средой.

Применение уравнения политропы к исследованию действительных процессов. Для исследования действительных процессов сжатия и расширения, протекающих в энергетических установках, производят замену этих процессов близкими к ним политропами. Подобная замена позволяет использовать весь математический аппарат термодинамического исследования.

Применяя представление индицированных реальных процессов в логарифмической системе координат <логарифмическую анаморфозу),действительную кривую линию заменяют прямой. Политропа в этой системе координат выражается прямой

с угловым коэффициентом, равным показателю политропы п (рис. 2.9), определяемым как

где а — острый угол, образованный прямой процесса с осью абсцисс.

Приближенно величина показателя политропы может быть вычислена и по формуле

Рис. 2.9. Политропный процесс

В целях повышения точности индикаторная линия может быть заменена рядом отрезков ломаной линии, для каждого из которых определяется свой показатель политропы.

На рис. 2.10 показана кривая сжатия 1— 1’—2, полученная при испытаниях двигателя внутреннего сгорания. Участки 1—1′ и 1’—2 кривой с достаточной степенью приближения могут быть заменены отрезками прямых, образующих углы оц и ос₂ с осью абсцисс. Измерением определено: tg с^ = = 1,53 и tg а₂ = 1,17.

Рис. 2.10. Действительная кривая сжатия

Таким образом, действительная кривая сжатия может быть заменена на участке от р_< до р’ политропой pv i > 53 = const, а на участке от р’ до р₂ — политропой рт 1 ’!? = const.

Если возможна меньшая точность расчетов, то вся кривая может быть заменена одной политропой pv x 37 = const, проходящей через начальную и конечную точки процесса.

Блог об энергетике

энергетика простыми словами

Основные термодинамические процессы

Основными процессами в термодинамике являются:

• изохорный, протекающий при постоянном объеме;
• изобарный, протекающий при постоянном давлении;
• изотермический, происходящий при постоянной температуре;
• адиабатный, при котором теплообмен с окружающей средой отсутствует;
• политропный, удовлетворяющий уравнению pv n = const.

Изохорный, изобарный, изотермический и адиабатный процессы являются частными случаями политропного процесса.

При исследовании термодинамических процессов определяют:

• уравнение процесса в p—v иT—s координатах;
• связь между параметрами состояния газа;
• изменение внутренней энергии;
• величину внешней работы;
• количество подведенной теплоты на осуществление процесса или количество отведенной теплоты.

Изохорный процесс

При изохорном процессе выполняется условие v = const.

Из уравнения состояния идеального газа (pv = RT) следует:

т. е. давление газа прямо пропорционально его абсолютной температуре:

Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).

Количество теплоты, подведенной к рабочему телу в процессе 1-2 при c_v = const определяется по формуле:

Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:

Изменение энтропии в изохорном процессе определяется по формуле:

Изобарный процесс

Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует:

т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.

Работа будет равна:

Количество теплоты при c_p = const определяется по формуле:

Изменение энтропии будет равно:

Изотермический процесс

При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно:

т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.

Работа процесса будет равна:

Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:

При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.

Изменение энтропии равно:

Адиабатный процесс

Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как dq = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:

В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.

Обозначим теплоемкость в адиабатном процессе через c_ад, и условие dq = 0 выразим следующим образом:

Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (c_ад = 0).

и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид:

В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона).

k_{выхлопных газов ДВС} = 1,33

Из предыдущих формул следует:

Техническая работа адиабатного процесса (l_техн) равна разности энтальпий начала и конца процесса (i₁ – i₂).

Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. В T, s-диаграмме он изображается вертикальной линией.

Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае ds > 0, и процесс называется реальным адиабатным процессом.

Политропный процесс

Политропным называется процесс, который описывается уравнением:

Показатель политропы n может принимать любые значения в пределах от -∞ до +∞, но для данного процесса он является постоянной величиной.

Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p, vи Tв любых двух точках на политропе:

Работа расширения газа в политропном процессе равна:

В случае идеального газа эту формулу можно преобразовать:

Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики:

представляет собой теплоемкость идеального газа в политропном процессе.

При c_v, k и n = const c_n = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью.

Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.

Графическое представление политропа в p, v координатах в зависимости от показателя политропа n.

pv 0 = const (n = 0) – изобара;

pv = const (n = 1) – изотерма;

p 0 v = const, p 1/∞ v = const, pv ∞ = const – изохора;

n > 0 – гиперболические кривые,

n По материалам моего конспекта лекций по термодинамике и учебника «Основы энергетики». Автор Г. Ф. Быстрицкий. 2-е изд., испр. и доп. — М. :КНОРУС, 2011. — 352 с.

1. К политропным
относятся процессы, подчиняющиеся
урав­нению

,
(2.27)

где
–
показатель политропы, который может
принимать значения ±∞.
Для данного политропного процесса
величина
постоянная.

2. Графики политропных
процессов. Политропный
процесс является обобщающим по отношению
к основным термодинамическим процессам.
Действительно:

• если
  ,
  то из уравнения политропного процесса
  получим уравнение
  изобарного процесса,
  т.к.
  
  или
  ;

• Рис. 2.10. График политропных процессов

  если
  ,
  тогда
  .
  Из уравнения состояния следует, что
  .
  Следовательно, значению
  соответствует уравнение изотермического
  процесса;

если
,
то из уравнения политропного процесса
получим уравнение адиабатного процесса
;

3. Связь между
параметрами состояния газа
в политропном процессе
аналогичны связи в адиабатном процессе,
а именно

,
.

4. Определение
количества теплоты q,
подведенной к газу, совершенной им
работы l
и изменения его внутренней энергии Δu:
По аналогии с адиабатным процессом:

• количество тепла,
  подведенного к газу
  ;

• изменение внутренней
  энергии газа
  
  ;

• работа газа в
  политропном процессе

,

5. Теплоемкость
политропного процесса.
Подставляя значения q,

и
в уравнение первого закона термодинамики,
получим

или
.

Окончательно для
политропного процесса теплоемкость
газа равна

.
(2.28)

Таким образом,
теплоемкость политропного процесса
зависит от показателя политропы
и рода газа, т.к.изависят от рода газа.

Теплоемкость в
каждом политропном процессе имеет
вполне определенную величину, зависящую
от значений
,
k
и
.
Причем, в зависимости от показателя
политропы, теплоемкость может быть
положительной или отрицательной, а в
отдельных случаях равной нулю (в
адиабат­ном процессе) или бесконечности
(в изотермическом процессе). Действительно,
в
соответствии
с (2.28):

• в изобарном
  процессе
  ,
  тогда
  ;

• в изотермическом
  процессе
  
  →
  ;

• в адиабатном
  процессе
  
  →
  ;

• в
  изохорном процессе
  →
  .

2.11. Анализ политропных процессов

1. Все процессы,
начинающиеся в точке «0»
на исходной изохоре
=(например, процессы0-1
или 0-2,
рис. 2.11) и идущие вправо от нее, совершаются
с увеличением удельного объема
(),
т.е. газ совершает работу расширения
против внешних сил,
т.к..

Процессы, исходящие из
точки «0», например, 0-3
и 0-4, и лежащие
левее исходной изохоры, протекают с
уменьшением
().
Здесь к газу подводится работа извне,
за счет чего он сжимается.

2. Во всех процессах,
начинающихся в точке «0», лежащей на
исходной изотерме Т₀
(рис. 2.12),
например, в процессах 0-1
или 0-2,
которые протекают вправо от исходной
изотермы, температура газа увеличивается
(),
поэтому его внутренняя энергия возрастает
().
В процессах0-3
или 0-4,
наоборот, ΔТ
< 0 и (Δu<
0).

3. Рассмотрим два процесса
расширения газа (рис. 2.13):

• 0-1
  – адиабатный, в котором q=0;

• 0-2
  – изотермический, в котором
  ,
  поэтому.

В соответствии с
первым законом термодинамики
в
изотермическом процессе0-2
газ расширяется (υ
> 0), совершая работу
,
за счет подвода к нему теплоты. Поэтому
в этом процессеq
> 0.

Таким образом,
все процессы, начинающиеся в точке «0»
на адиабате и протекающие вправо от
адиабаты, совершаются с подводом к газу
теплоты (q
> 0), а процессы, протекающие влево от
адиабаты – с отводом от газа теплоты.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

2018-05-21

Уравнение состояния газа

При изучении термодинамических процессов, воздух считают идеальным газом, то есть таким газом, у которого молекулы бесконечно малы по объему, но имеют конечную массу, а силы взаимодействия между молекулами отсутствуют.

Это уравнение связывает основные физические величины, характеризующее состояние газа:

• р — давление
• V — объем
• Т — температура
• m — масса

Газовая постоянная R равна работе расширения, совершаемой 1 кг газа при нагревании его на 1 К при постоянном давлении.

R = c_p — c_v
Для воздуха R= 287 Дж/(кг)×К

При сжатии и расширении газа изменяются его характеристики. На основе уравнения состояния могут быть получены зависимости состояния газа (воздуха) при различных процессах, которые характеризуются разными условиями протекания.
Рассмотрим каждый из возможных характерных процессов отдельно.

Изотермический процесс

Изотермическим называют термодинамический процесс, протекающий при постоянной температуре. При Т₁ = Т₂, согласно закону Бойля-Мариотта, pV=const, поэтому при изотермическом процесс давление газа будет обратно пропорционально его объему.

p₁/p₂ = V₂/V₁

Изобарный процесс

Изобарным называют термодинамический процесс, протекающий при постоянном давлении. При Т₁ = Т₂, отношение объема данной массы газы к температуре остается постоянным, то есть:

V₁/V₂ = Т₁/Т₂

Изохорный процесс

Изохорным называют процесс, протекающий при постоянном объеме. Если V₁ = V₂, то отношение давления к температуре также будет постоянным.

р₁/р₂ = Т₁/Т₂

Адиабатический процесс

Адиабатическим или адиабатным называют такой процесс, при протекании которого теплообмен с окружающей средой отсутствует. Для такого процесса справедлива формула Пуассона:

pV^k = const

Где k — показатель адиабаты k = c_p/c_v (для воздуха k=1,4). Зависимости между физическим величинами, характеризующими состояние газа при адиабатном процессе выглядят следующим образом:

Политропный процесс

Политропным называют процесс, протекающий с теплообменом между газом и окружающей средой. Для этого процесса справедливо уравнение политропы:

pVⁿ = const

Где n — показатель политропы n = (c_p — c)/(_v — c), для расчета пневмоприводов n выбирают из диапазона 1,25…1,35.

Зависимости между основными параметрами газа при политропном процессе выглядят следующим образом:

В общем случае, процессы протекающие в пневматическом приводе следует считать политропными.

На практике медленно текущие процессы, с некоторыми допущениями, можно считать изотермическими, быстротекущие процессы адиабатными.

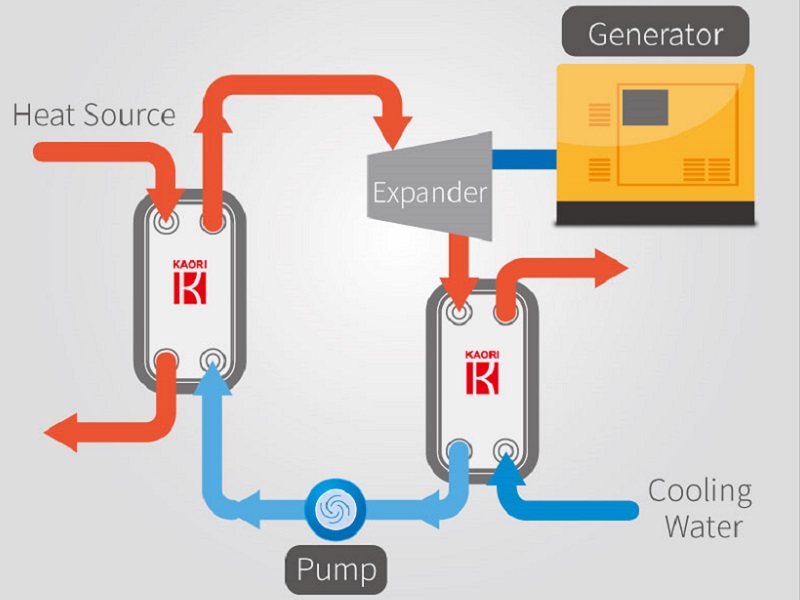
1.2 Исследование политропного процесса сжатия в компрессоре

В одноступенчатом поршневом компрессоре воздух сжимается от давления – р₁ , =0.1 МПа абс. при температуре — t₁ =17°С до давления р₂ =0,45 МПа абс.

Стенки цилиндра компрессора охлаждаются водой так, что процесс сжатия воздуха в компрессоре является политропным.

Показатель политропы сжатия -n =1,33

Производительность компрессора, измеренная по месту всасывания: V₁ =300 м³/ҹ

Температуру сжатого воздуха — t₂ °С.

Объем сжатого воздуха — V₂ м³/ч.

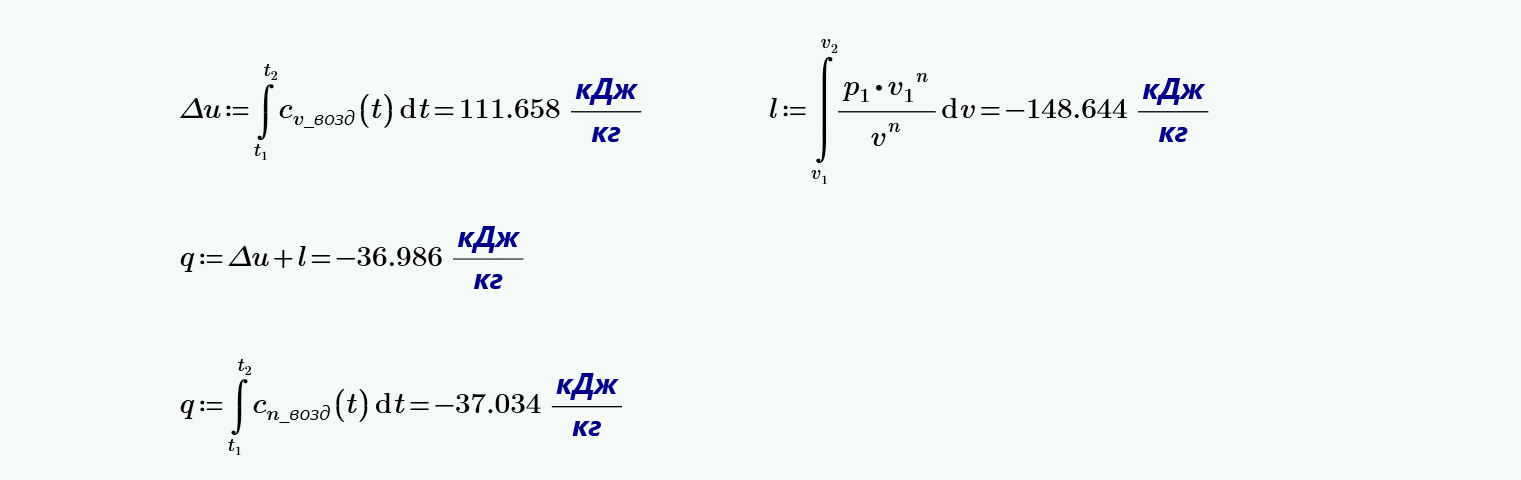
Изменение внутренней энергии и энтальпии воздуха при сжатии.

Затрачиваемую работу в процессе и теоретически необходимую мощность для привода компрессора — N₀ кВт.

Количество теплоты, отводимой от воздуха при сжатии, и, соответственно, количество охлаждающей воды — М кг/ч, полагая, что вода нагревается от 10°С до 20° С.

Диаметры всасывающего и нагнетательного воздухопроводов компрессора, принимая скорость в них — W= 12м/сек.

Построить графики процесса сжатия в pv-диаграмме.

Построить графики в ‘Тs-диаграмме по точкам процесса сжатия, а также изобар, между которыми расположен процесс сжатия. Сделать соответствующее обозначение площадей под кривыми.

Указать характер превращения энергии. При исследовании принять:

В связи с изменением условий охлаждения стенок компрессора, показатель политропы сжатия увеличивается — уменьшается до n =1,05. Определить для новых условий температуру воздуха — t₂ °С и количество отводимой теплоты q

Вывод: с уменьшением n от 1.33 до 1.05 температура воздуха не изменяется (17°С) количество отведенной теплоты изменилось с -19.924 до -107.918. Процесс близок к изотермическому.

Источник

Задание исследование политропного процесса1

Нижегородский Государственный Технический Университет

Кафедра «Энергетические установки и тепловые двигатели»

ИССЛЕДОВАНИЕ ПОЛИТРОПНОГО ПРОЦЕССА СЖАТИЯ ВОЗДУХА В ОДНОСТУПЕНЧАТОМ КОМПРЕССОРЕ.

Выполнил: студент гр. 15-КС-1

Политропный процесс — термодинамический процесс, во время которого теплоёмкость газа остаётся неизменной.

В соответствии с сущностью понятия теплоёмкости , предельными частными явлениями политропного процесса являются изотермический процесс и адиабатный процесс.

В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными (удельные теплоёмкости идеального газа при постоянном объёме и постоянном давлении соответственно равны и где — универсальная газовая постоянная, — молярная масса, — число степеней свободы) и не меняются при изменении термодинамических параметров).

Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде: 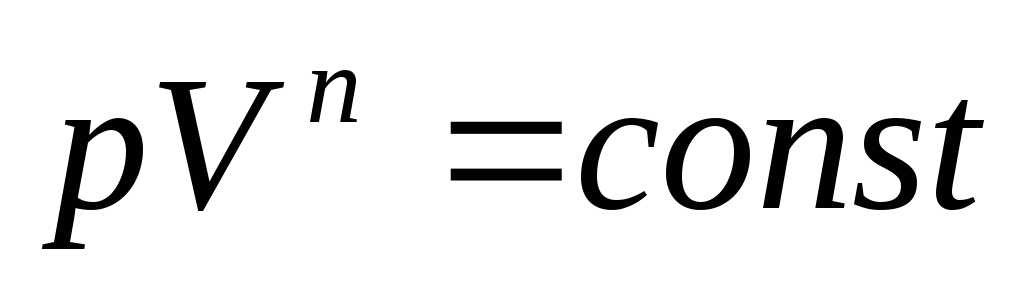, где P — давление, V — объем газа, n — показатель политропы, причем

C — теплоемкость газа в данном процессе, C_p и C_V — теплоемкости газа при постоянном объеме и давлении.

В зависимости от вида процесса, можно определить значение n:

Изотермический процесс:

Изобарный процесс:

Адиабатный процесс: 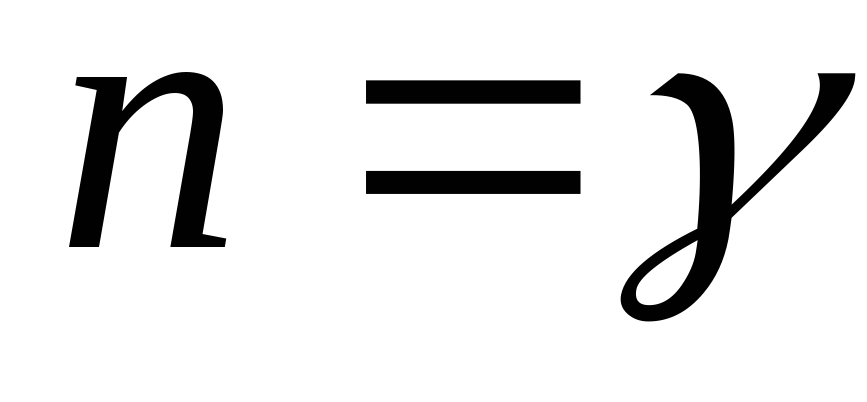; γ — показатель адиабаты

Изохорный процесс:

Сжатый воздух получается с помощью различного типа компрессоров. Компрессоры низкого давления называют вентиляторами и применяют для перемещения и подачи воздуха в калориферы сушильных установок, воздухоподогреватели, топки, а также для преодоления сопротивления движению газов, чтобы обеспечить тягодутьевой режим в различных установках. По принципу устройства и работы компрессоры делятся на две группы – объемные и лопаточные. Объемные компрессоры подразделяются на поршневые и ротационные, а лопаточные – на центробежные и осевые (аксиальные). Несмотря на конструктивные различия термодинамические принципы их работы аналогичны между собой. Объемный компрессор – это компрессор статического сжатия, которое происходит в нем вследствие уменьшения объема, где заключен газ.

В одноступенчатом поршневом компрессоре воздух сжимается от давления – р₁ , =0.1 МПа абс. при температуре — t₁ =17°С до давления р₂ =0,45 МПа абс.

Стенки цилиндра компрессора охлаждаются водой так, что процесс сжатия воздуха в компрессоре является политропным.

Показатель политропы сжатия -n =1,33

Производительность компрессора, измеренная по месту всасывания: V₁ =300 м³/ҹ

Температуру сжатого воздуха — t₂ °С.

Объем сжатого воздуха — V₂ м³/ч.

Изменение внутренней энергии и энтальпии воздуха при сжатии.

Затрачиваемую работу в процессе и теоретически необходимую мощность для привода компрессора — N₀ кВт.

Количество теплоты, отводимой от воздуха при сжатии, и, соответственно, количество охлаждающей воды — М кг/ч, полагая, что вода нагревается от 10°С до 20° С.

Диаметры всасывающего и нагнетательного воздухопроводов компрессора, принимая скорость в них — W= 12м/сек.

Построить графики процесса сжатия в pv-диаграмме.

Источник

Компрессоры

Задача 262

Условие задачи: Поршневой компрессор подает V=2,4 м3 воздуха в минуту (объем приведен к нормальным условиям). За какое время данный компрессор сможет поднять давление воздуха в ресивере от p1=0,2 МПа до p2=0,8 МПа. Объем ресивера Vр=5 м3, температура воздуха t=20ºC.

задача230

Условие задачи: Для технологических целей необходимо иметь G кг воздуха в секунду при давлении р1. Рассчитать идеальный многоступенчатый поршневой компрессор. Определить количество ступеней компрессора и степень повышения давления в каждой ступени, количество теплоты отведенной от воздуха в цилиндрах компрессора и в промежуточном холодильнике, конечную температуру и объемную производительность. Изобразить цикл на рабочей диаграмме. Давление воздуха на входе в первую ступень компрессора р1=0,1 МПа и температура t1=27°C. Допустимое повышение температуры воздуха в каждой ступени Δt=175°C; показатель политропы сжатия n=1,25; конечное давление воздуха рк=17 МПа; массовый расход воздуха G=0,4кг/с. При решении задачи трение и вредное пространство не учитывать; степени повышения давления в каждой ступени компрессора считать одинаковыми и привести в соответствие с допустимым повышением температуры.

Задача 224

Условие задачи: Определить теоретическую мощность привода одноступенчатого компрессора при изотермическом сжатии воздуха, если его производительность при начальных параметрах р1= 0,1МПа и t1=15°C, составляет V1= 0,1 м3/c, а конечное давление р2= 0,7 МПа. Определить также расход охлаждающей воды, если температура её повышается в рубашке компрессора на Δt=20 °C.

Задача 220

Условие задачи: Смесь, состоящая из двух газов Н2 и СО, заданная массовыми долями m1=0,3 и m2=0,7 соответственно, при начальном давлении р1=0,4 МПа и температуре t1=-3º C, сжимается в компрессоре по изотерме, адиабате и политропе с показателем n=1,3. Определить для трёх вариантов величину теоретической работы сжатия, мощность привода компрессора, а также изменение внутренней энергии и энтропии при сжатии, если степень сжатия ε=v1/v2=5, а расход воздуха G=20 кг/мин. Теплоёмкость воздуха принять Cv=f(t)=const.

Прочитать больше

Задача 215

Условие задачи: Расход газа в поршневом одноступенчатом компрессоре составляет V1 = 55 м3/мин; при давлении р1= 0,1МПа и температуре t1=22°C. При сжатии температура газа повышается на 200°C. Сжатие происходит по политропе с показателем n=1,5. Определить конечное давление, работу сжатия и работу привода компрессора, количество отведенной теплоты, а также теоретическую мощность привода компрессора.
Указание: При расчете принять k= сv/сp= const. Газ – Гелий.

Задача 209

Условие задачи: Производительность воздушного компрессора при начальных параметрах p1=1 бар, и t1=25ºС и конечном давлении p2= 6 бар, составляет G=500 кг/ч. Процесс сжатия воздуха в компрессоре изотермический. Отношение хода поршня к диаметру цилиндра S/D=1,2. Частота вращения вала n=300 мин-1. Определить теоретическую мощность двигателя для привода компрессора, ход поршня и диаметр цилиндра, а также расход охлаждающей воды через рубашку охлаждения компрессора, если температура воды повышается на Δt=15ºС.

Задача 184

Условие задачи: Рассчитать эффективную мощность на валу поршневого одноступенчатого неохлаждаемого компрессора, сжимающего кислород. Параметры, сжимаемого газа: р1=0,0981 МПа и температура t1=20°C. Степень повышения давления – β=7.Эффективный КПД – ηк=0,7. Геометрические размеры цилиндра: длина hц=250мм, диаметр d=120мм, ход поршня h=240 мм. Вал компрессора совершает 240 об/мин. Принять коэффициент наполнения цилиндра равным объемному коэффициенту, то есть параметры всасываемого газа равны параметрам среды, а утечки отсутствуют.

Задача 177

Условие: Для теоретического одноступенчатого воздушного компрессора определить секундную работу, затрачиваемую на его привод, если подача компрессора при начальных параметрах воздуха (p1=0,l МПа и t1=17°С) составляет V= 0,15 м3/с. Сжатие газа до конечного абсолютного давления р2=0,5 МПа, протекает по политропе с показателем n =1,2. Определить также расход воды, если температура ее в охлаждающей рубашке компрессора повысилась на Δt=20°С.

Вопрос 1

Как изменится удельная техническая работа компрессора, если сжатие воздуха проводить двухступенчато с полным промежуточным охлаждением до начальной температуры и при одинаковых значениях показателя политропы сжатия и степени повышения давления в каждой ступени? Графически проиллюстрировать изменение работы

Задача 112

Условие задачи: Для технологических целей необходимо иметь G кг воздуха в секунду при давлении р1. Рассчитать идеальный многоступенчатый поршневой компрессор. Определить количество ступеней компрессора и степень повышения давления в каждой ступени, количество теплоты отведенной от воздуха в цилиндрах компрессора и в промежуточном холодильнике, конечную температуру и объемную производительность. Изобразить цикл на рабочей диаграмме. Давление воздуха на входе в первую ступень компрессора р1=0,1 МПа и температура t1=27°C. Допустимое повышение температуры воздуха в каждой ступени Δt=185°C; показатель политропы сжатия n=1,23; конечное давление воздуха рк=19 МПа; массовый расход воздуха G=0,2кг/с. При решении задачи трение и вредное пространство не учитывать; степени повышения давления в каждой ступени компрессора считать одинаковыми и привести в соответствие с допустимым повышением температуры.

Источник

Energy
education

сайт для тех, кто хочет изучать энергетику

Термодинамика и тепломассообмен

Термодинамические циклы

Термодинамические циклы — круговые процессы в термодинамике, то есть такие процессы, в которых совпадают начальные и конечные параметры, определяющие состояние рабочего тела.

Примеры решения задач по теме «Компрессоры»

1. Компрессор всасывает $400$ м 3 /ч воздуха при давлении $p_1=0.1$ МПа и температуре $t_1=20$ °С и сжимает его до давления $p_2=0.5$ МПа. Определить теоретическую работу компрессора при адиабатном сжатии и температуру воздуха в конце сжатия.

2. Компрессор всасывает $100$ м 3 /ч воздуха при давлении $p_1=0.1$ МПа и температуре $t_1=27$ °С. Конечное давление воздуха составляет $p_2=0.8$ МПа. Определить теоретическую работу компрессора и расход охлаждающей воды, если ее температура повышается на $13$ °С. Расчет произвести для изотермического, адиабатного и политропного сжатия. Показатель политропы принять равным $1.2$, а теплоемкость воды $4.19$ кДж/кг·К.

3. Определить мощность идеального компрессора с изотермическим сжатием и часовое количество теплоты, передаваемое охлаждающей водой, если $p_1=101325$ Па и $t_1=20$ °С, а давление сжатого воздуха $p_2=0.4$ МПа. Расход всасываемоего воздуха $500$ м 3 /ч.

4. Компрессор всасывает $250$ м 3 /ч воздуха при $p_1=0.09$ МПа и $t_1=25$ °С и сжимает его до $p_2=0.8$ МПа. Какое количество воды нужно пропускать через рубашку компрессора в час, если сжатие происходит политропно с показателем $n=1.2$ и температура воды повышается на $15$ °С.

5. Компрессор всасавает воздух при давлении $0.1$ МПа и температуре $20$ °С и сжимает его изотермически до $0.8$ МПа. Определить производительность компрессора в м 3 /ч, если известно, что теоретическая мощность двигателя для привода компрессора равна $40$ кВт. Найти также часовой расход охлаждающей воды, если ее температура при охлаждении цилиндра компрессора повышается на $10$ °С. Теплоемкость воды принять равной $4.19$ кДж/кг·К.

6. Компрессор всасывает в минуту $100$ м 3 водорода при температуре $20$ °С и давлении $0.1$ МПа и сжимает его до $0.8$ МПа. Определить потребную мощность двигателя для привода компрессора при адиабатном сжатии, если эффективный КПД компрессора равен $0.7$.

7. Трехступенчатый компрессор всасывает $60$ м 3 /ч воздуха при $p_1=0.08$ МПа и $t_1=27$ °С и сжимает его адиабатно до $10$ МПа. Между ступенями компрессора установлен промежуточный холодильник, в котором воздух охлаждается при постоянном давлении до начальной температуры. Определить производительность компрессора по сжатому воздуху и работу, затраченную на сжатие в компрессоре.

8. Двухступенчатый компрессор всасывает воздух при давлении $p_1=0.1$ МПа и температуре $t_1=20$ °С и сжимает его до конечного давления $p_2=4$ МПа. Между ступенями компрессора установлен промежуточный холодильник, в котором воздух охлаждается при постоянном давлении до начальной температуры. Производительность компрессора равна $500$ м 3 /ч.

Определить теоретическую мощность каждой ступени и количество теплоты, которое должно быть отведено от обеих ступеней компрессора и промежуточного холодильника, если известно, что отношение конечного давления к начальному одинаково для обоих ступеней и сжатия происходит политропно с показателем $n=1.3$.

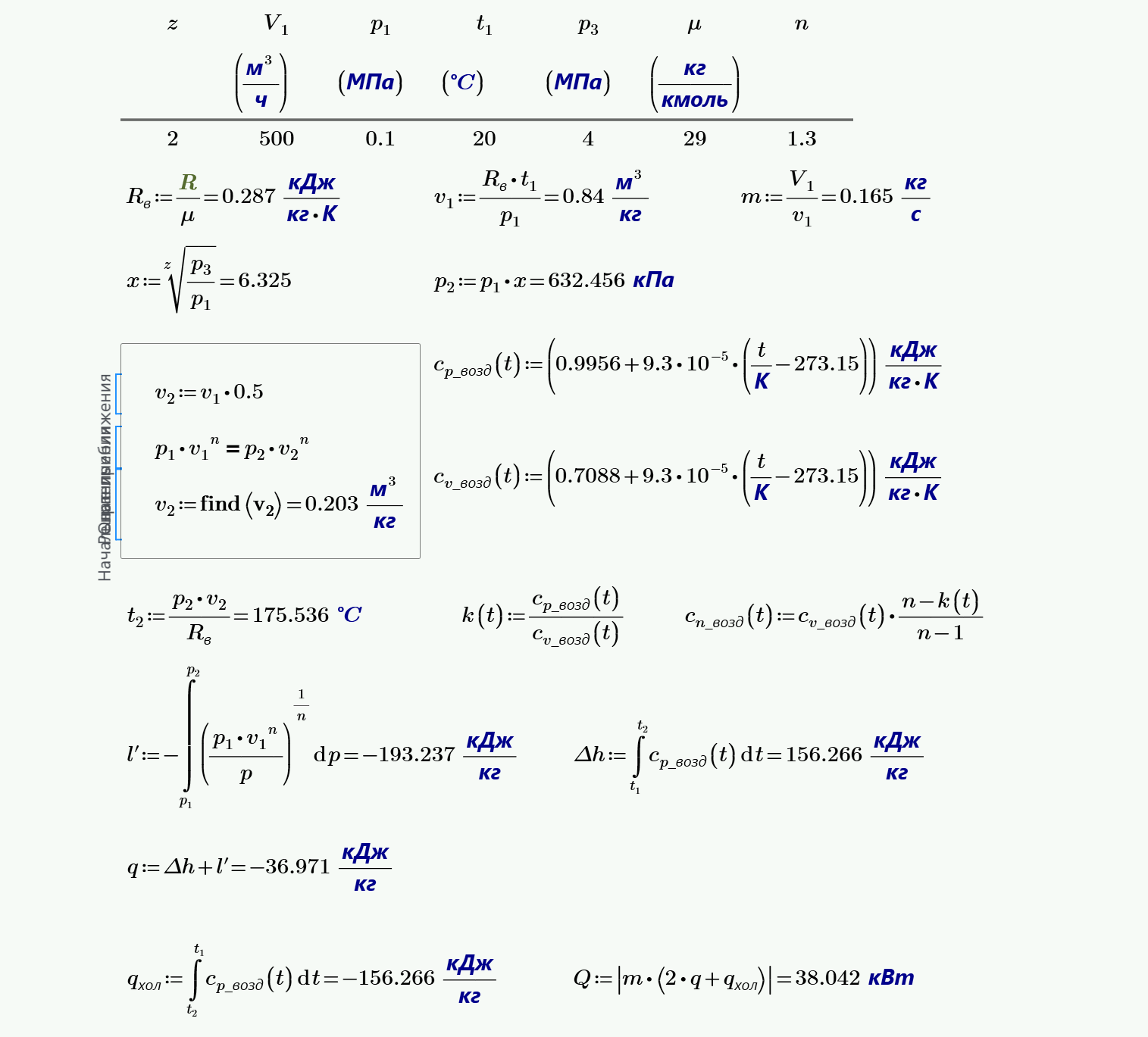
9. Для лабораторных экспериментов необходимо иметь $G=180$ килограммов в секунду воздуха при параметрах $p_к=10$ МПа и $t_к=t_1$, где $t_1$ − температура окружающей среды. Рассчитать поршневой компрессор (без учета трения и вредного пространства), определить: количество ступеней компрессора; степень повышения давления в каждой ступени; количество тепла, отведенного от воздуха в цилиндрах компрессора, в промежуточных и конечном холодильниках (при охлаждении до $t_1$); мощность привода, если давление воздуха на входе в первую ступень компрессора $p_1=0.1$ МПа, а температура $t_1=27$ °С и допустимое повышение температуры воздуха в каждой ступени $Δt=180$, показатель политропы сжатия $n=1.25$.

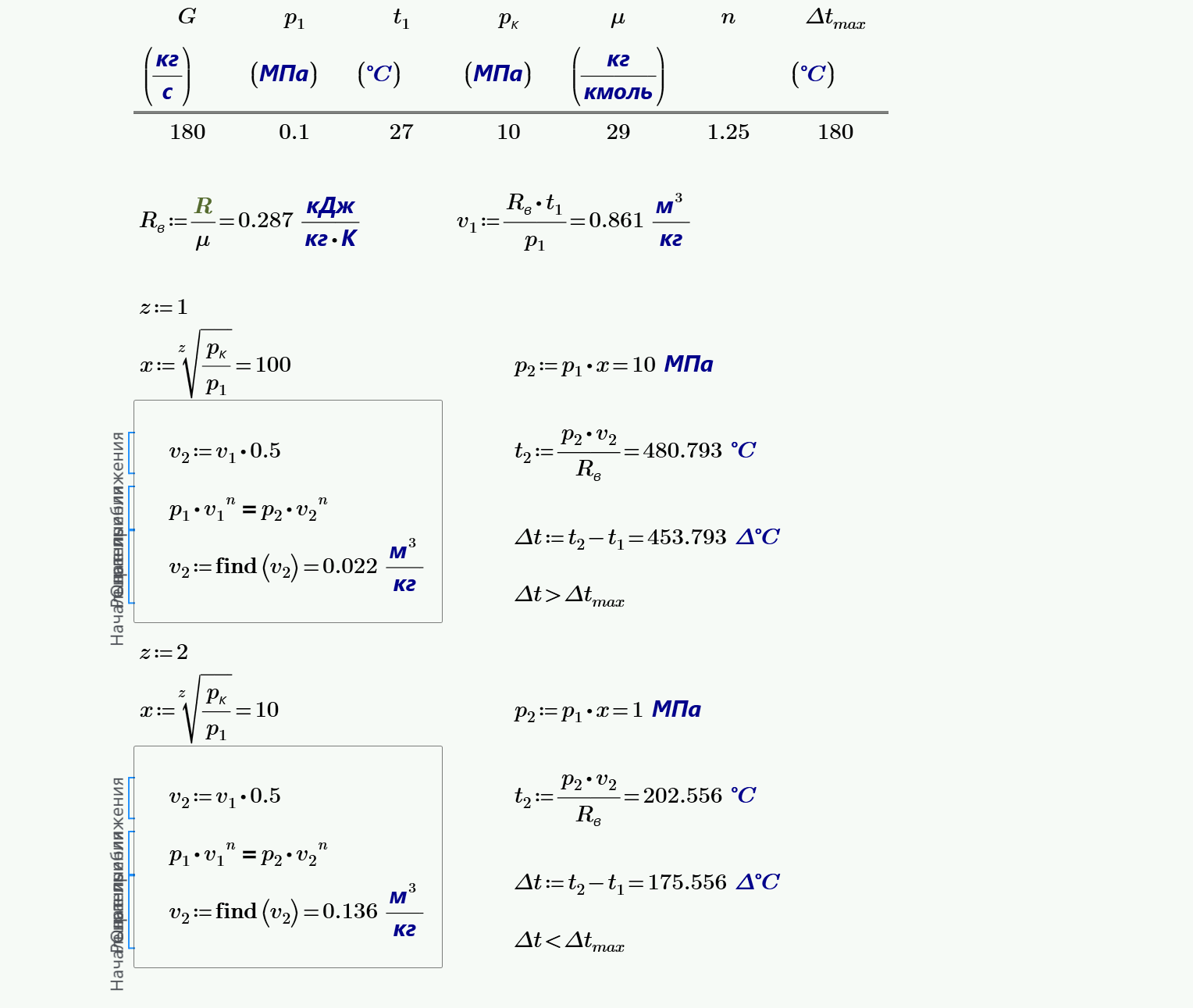
10. Для двигателя с воспламенением от сжатия необходим трехстепенчатый компрессор, подающий $250$ кг/ч воздуха при давлении $8$ МПа. Определить теоретическую мощность компрессора. Сжатие считать адиабатным. В начале сжатия $p_1=0.095$ МПа и $t_1=17$ °С.

Администратор сайта: Колосов Михаил
email:
Copyright © 2011-2021. All rights reserved.

Источник