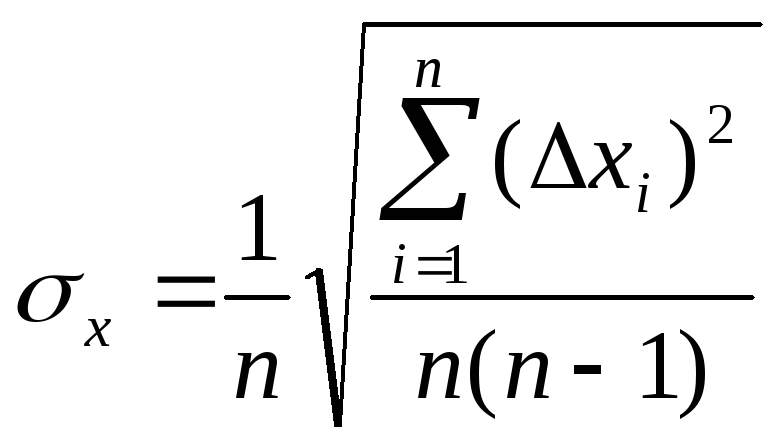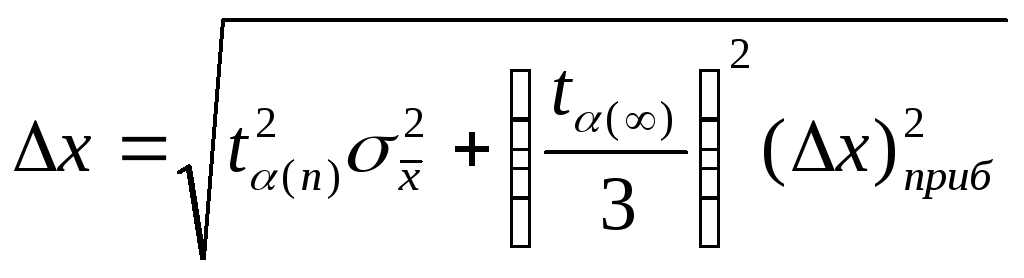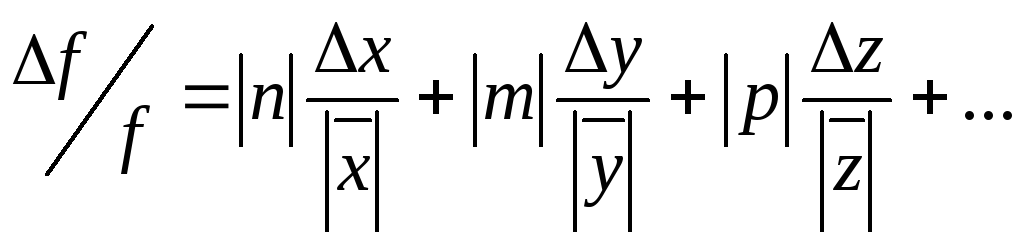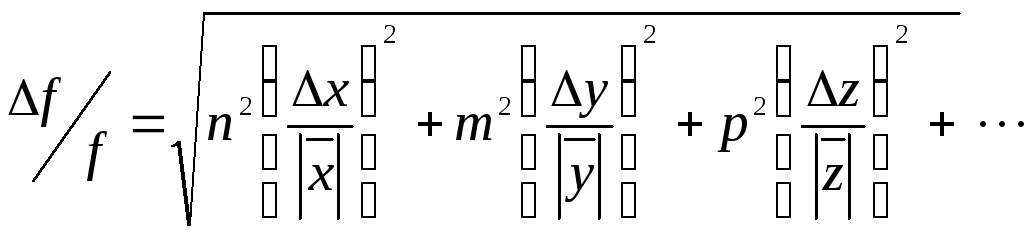Как найти погрешность косвенных измерений формула

26

В
результате прямого измерения получается
не истинное значение х
измеряемой величины, а серия
изn
значений
.
Пусть теперь

Суммируя последнее
равенство, получим

или

Но

(7)

где
средне арифметическое измеренных
значений.
Таким образом,

(8)

Из
этого простого результата вытекают
весьма важные следствия. Действительно,
при
и.

значит,
при бесконечно большом числе измерений
и, следовательно, при конечныхn
результат тем ближе к среднему
арифметическому, чем больше число
измерений. Отсюда также следует, что
при оценке ∆Х
в качестве

целесообразно
взять
.

На
практике n
конечно и
.
В задачу математической теории случайной
погрешности входит оценка интервала

(9)

в
котором заключено истинное значение
измеряемой величины. Интервал (9)
называется доверительным
интервалом,
а величина
–абсолютной
погрешностью результата серии измерений.
Теория оценки ∆х
достаточно сложна, поэтому здесь будут
рассмотрены лишь её основные результаты.
Прежде всего нужно отметить, что,
поскольку х
– случайная величина, ошибка ∆х
может быть определенна лишь с той или
иной степенью надежности
α,
которую также называют доверительной
вероятностью.
Доверительная вероятность – это
вероятность того, что истинное значение
измеряемой величины х
попадает в доверительный интервал (9).
Если положить α=1
(100%), то это будет соответствовать
достоверному событию, т.е. вероятности
того, что х
принимает
какое-то значение в интервале ().
При этом.
Очевидно, такой выбор надёжностиα
нецелесообразен.
При малых α
доверительный интервал ∆х
определяется с малой достоверностью.
В дальнейшем мы будем полагать α=0.90
или 0.95. Доверительный интервал и
надёжность взаимосвязаны. Для оценки
границ доверительного интервала
английский математик В. Госсет
(публиковавший свои работы под псевдонимом
Стьюдент) ввёл в 1908 г. коэффициент:

(10)

равный
отношению погрешности ∆х
к средней
квадратичной ошибке*

(11)

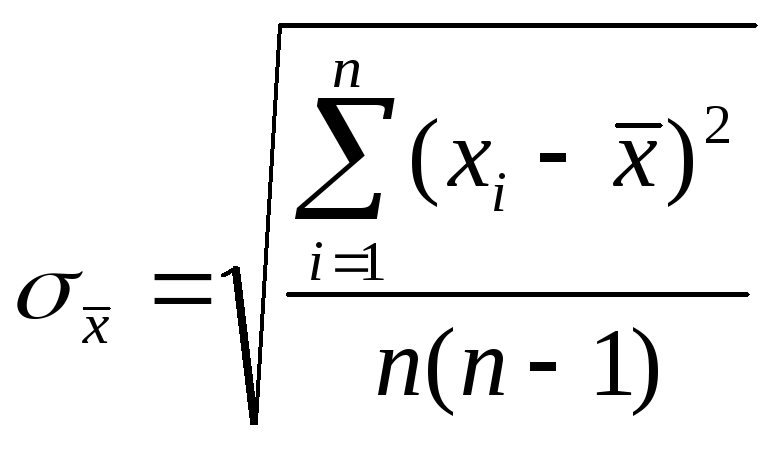
Коэффициент
зависит от надёжностиα,
а также от числа измерений n
и называется коэффициентом
Стьюдента.
Этот коэффициент табулирован (см.
приложение 1), поэтому рассчитав
и задав доверительную вероятностьα,
нетрудно найти случайную ошибку:

(12)

Расчёт погрешности косвенных измерений.

При
косвенных измерениях измеряемая величина
f
находится
из функциональной зависимости:

где
x,
y,
z
– результаты прямых измерений. Формулу
для ∆f
можно
получить, заменив в (2) дифференциалы
погрешностями и взяв все слагаемые по
модулю

(13)

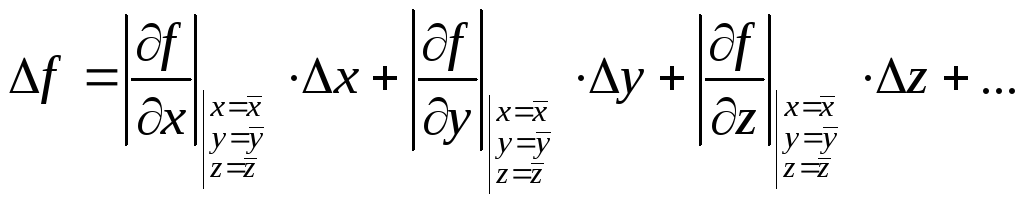
Соотношение
(13) рекомендуется для оценки погрешности
∆f
, обусловленной
приборными погрешностями величины x,
y, z,… Для
оценки погрешности, связанной со
случайными ошибками прямых измерений,
рекомендуется соотношение:

(14)

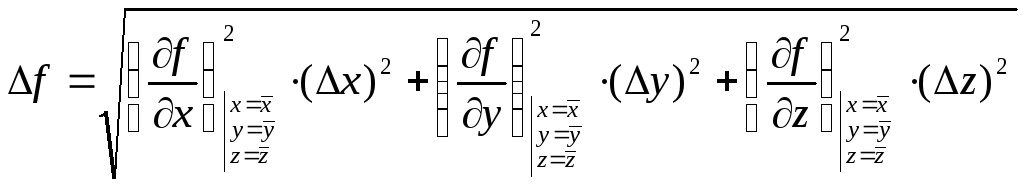
Следует
правда отметить, что формулы (13) и (14)
приводят практически к одинаковым
результатам. Производные в (13) и (14)
берутся при средних, т.е. при измеренных
значениях аргументов.

Очень
часто функция f
представлена
степенной зависимостью от аргументов

(15)

где
c, n, m и p – постоянные. Частным случаями
формулы (15) являются соотнощения
,и
др.

Задание.
Покажите, что для функции вида (15) формулы
(13) и (14) принимают вид:

(13)

(14)

Из
соотношений (13) и (14) следует, что для
степенных функций расчёт погрещностей
существенно упрощается, причём
целесообразно сначала найти относительную
погрешность, которая выражается через
относительную погрешность прямых
измерений, а затем найти абсолютную
погрешность

(16)

Под
понимается
функция от средних (измеренных) значений
аргументов

.

Алгоритм расчета погрешностей

—
Для прямых измерений

1.
Вычислить среднее арифметическое
результатов

серии из n
измерений:

Замечание:
при расчете
удобнее исходить из формулы:

где
— любое удобное значение, близкое к.

2. Найти отклонения
отдельных измерений от среднего значения

3. Исключить промахи.

4. Рассчитать
среднюю квадратичную погрешность
результата серии измерений

Замечание.
При

можно положить

и рассчитывать
по формуле

5.
Если
,
то случайную ошибку можно не рас­считывать.

6.
В противном случае задать доверительную
вероятность
и найти по таблице коэффициент Стьюдента
.

7. Рассчитать
границы доверительного интервала

Замечание
1. Если
приборная погрешность
имеет тот же порядок величины что и, то абсолютная погрешность результата
серии измерений находится по формуле:

где
Практически в качествеможно
взять табличное значениеотвечающее самому большо­му из
приведенных в ней значенийп
(например, п=500
).

Замечание
2. При большом
числе измерений
можно по­ложить

где

.

8. Результат
измерения представить в виде:

— Для косвенных
измерений

Погрешность

косвенного
измерения можно рассчитать по одной из
формул (13), (14), (13*), (14*). Две последние
формулы выпол­няются для степенных
зависимостей, а соотношения (13) и (14)
име­ют общий характер.

Сводка
соотношений для расчета погрешности
косвенного измере­ния
для
некоторых простых функциональных
за­висимостей представлена в таблице.

Таблица

Пример.
Пусть джоулево тепло Q рассчитывается
по формуле

Поскольку это
степенная зависимость, целесообразно
воспользоваться формулой (13*)

Правила
представления результатов измерений
и их погрешностей

Погрешности
могут лишь оцениваться, поэтому обычно
достаточно указать погрешность с одной
значащей цифрой. Например, Δm=0,2 г.
г.
Запись т
= 3,0 г
означает, что измерение произведено
с точностью до десятых долей грамма.
Однако при про­межуточных вычислениях
целесообразно оставлять больше значащих
цифр.

Правила округления
чисел (результатов измерений)
иллюстрируют­ся в таблице (обратите
внимание на особенности округления
цифры 5).

Таблица Округление
до десятых значащих цифр

Результат измерения
принято округлять так, чтобы числовое
зна­чение оканчивалось цифрой того
же разряда, что и значение погреш­ности.
Например, запись

см.

непреемлема,
т.к. само значение погрешности Δl = 0,1 см
указыва­ет
на то, что
цифры 018 результата не могут гарантироваться.
Нуж­но
записать
так:
см.

Соседние файлы в предмете Физика

• #
• #
• #

Как определять погрешности измерений

Измерение – нахождение значения физической величины
опытным путем с                   помощью средств измерений.

Прямое
измерение
– определение значения физической
величины непосредственно средствами измерения.

Косвенное
измерение
– определение значения физической
величины по формуле, связывающей ее с другими физическими величинами, определяемыми
прямыми измерениями.

          А,  В, С, … — физические величины.

          А_пр. – приближенное значение физической величины.

         А – абсолютная погрешность измерения физической
величины.

          — относительная погрешность измерения
физической величины.

          _иА
– абсолютная
инструментальная погрешность, определяемая конструкцией прибора.

          _оА – абсолютная погрешность отсчета, она равна в
большинстве случаев

                     половине цены деления; при
измерении времени – цене деления секундомера или часов.

          Абсолютную погрешность измерения
обычно округляют до одной значащей цифры:

          Численное значение результата
измерений округляют так, чтобы его последняя цифра оказалась в том же разряде,
что и цифра погрешности:

          
Результат
измерения записывается так:

       %

      
Определение погрешности методом среднего арифметического

          При многократных
измерениях величины погрешность можно оценить следующим образом:

1.    
Определить среднее
значение величины А:

 (при трех
измерениях).

2.Определить отклонение каждого значения от среднего:

     3.Определить среднее значение отклонения,
его и принимают за абсолютную погрешность:

   4.Определить
относительную погрешность и выразить ее в процентах:

          Многократные измерения
предпочтительнее, так как при их проведении возможна компенсация случайных
факторов, влияющих на результат. Обычно многократные измерения проводят, слегка
изменяя условия опыта, но предполагая, что значение величины А не изменяются

Определение
погрешности косвенных измерений

          При косвенных измерениях значение
физической величины находится путем    расчетов по формуле.

      Относительную погрешность
определяют так, как показано в таблице:

     Абсолютную погрешность определяют
по формуле:

(  выражается десятичной дробью)

    Пример:  пусть измеряется сопротивление проводника. .

   Результаты прямых измерений:     

    Тогда ;                                                                                                    
,    ;                                                                
,       ;                                             
,     ,   .

Графическое
представление результатов эксперимента

                                   Правила  построения
 графиков

          Для построения графиков выпускают
специальную бумагу-миллиметровку.

          При выборе масштабов по осям
координат следует руководствоваться следующими правилами:

         — значение независимой переменной
откладывают вдоль оси абсцисс, функции – вдоль оси ординат;

         — цена наименьшего деления масштабной
сетки должна быть сравнимой с величиной погрешности измерения;

         — точка пересечения оси абсцисс и оси
ординат не обязательно должна иметь координаты (0,0).

          При построении графиков следует
иметь в виду, что по результатам опытов мы получаем не точку, а прямоугольник
со сторонами  и.

                    
В

                       0                                                                        
А

          При выполнении простых лабораторных
работ достаточно обвести экспериментальную точку кружком или пометить
крестиком, не указывая доверительных интервалов.

          Этот кружок или крестик будут
обозначать, что данная точка получена с каким-то приближением и истинное
значение измеряемой величины лежит где-то в ее окрестности. 

Правила
приближенных вычислений

 1. Основное
правило округления.

Если первая
отброшенная цифра равна 5 или больше, то последнюю из сохраняемых цифр
увеличивают на единицу; если первая отброшенная цифра меньше 5, то последнюю из
сохраняемых цифр оставляют без изменения, например:

 2. При сложении и
вычитании приближенных чисел
в полученном результате сохраняют столько десятичных знаков, сколько их в числе
с наименьшим количеством десятичных знаков, например:

 3. При умножении
и делении приближенных чисел
в полученном результате нужно сохранить столько значащих цифр, сколько их имеет
приближенное число с наименьшим количеством значащих цифр, например:

 4. При возведении
в квадрат приближенного числа
нужно в результате сохранять столько значащих цифр, сколько их имеет возводимое
в степень число, например:

 5. При извлечении
квадратного корня в результате
нужно сохранять столько значащих цифр, сколько их имеет подкоренное число,
например:

 6. При вычислении
промежуточных результатов в
них следует сохранять на одну цифру больше, чем требуют правила 2-5. Причем при
подсчете значащих цифр запасные цифры не учитываются. В окончательном
результате запасная цифра отбрасывается   по основному правилу округления.

 7. При нахождении
углов или тригонометрических функций значение соответствующего угла записывают с точностью до градуса, если
значение тригонометрической функции имеет две значащие цифры; если угол задан с
точностью до градусов, то в значении тригонометрической функции сохраняют две
значащие цифры, например: