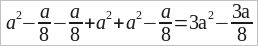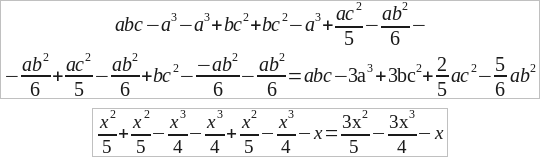Подобные слагаемые
- Свойства сложения и умножения
- Подобные слагаемые
- Приведение подобных слагаемых
Свойства сложения и умножения
В буквенных выражениях числа могут быть обозначены буквами. Поэтому для всех буквенных выражений верны следующие равенства, выражающие свойства сложения и свойства умножения:
| Свойства сложения | Свойства умножения |
|---|---|
| a + b = b + a (a + b) + c = a + (b + c) a + 0 = a a + (-a) = 0 a — b = a + (-b) |
ab = ba (ab)c = a(bc) a(b + c) = ab + ac a = 1 · a —a = -1 · a a · 0 = 0 |
С помощью этих свойств можно упрощать буквенные выражения. Например:
5a + 12a — 7a = (5 + 12 — 7)a = 10a.
Слагаемые 5a, 12a и -7a отличаются только числовыми множителями, такие слагаемые называются подобными.
Подобные слагаемые
Подобные слагаемые — это слагаемые, отличающиеся только числовыми множителями и имеющие одинаковую буквенную часть. Пользуясь свойствами сложения и умножения, можно упрощать выражения, содержащие подобные слагаемые. Например, упростим выражение:
10x — 9x = (10 — 9)x = 1 · x = x.
Такое упрощение выражения называется приведением подобных слагаемых. В простых примерах промежуточные вычисления можно опустить:
10x — 9x = x.
Приведение подобных слагаемых
Приведение подобных слагаемых — это упрощение выражения, содержащего подобные слагаемые, путём их сложения.
Пример 1. Приведите подобные слагаемые:
4x — 3y + y — 2x.
Решение: Сначала надо найти в выражении подобные слагаемые:
| 4x | — | 3y | + | y | — | 2x | , |
теперь можно их сгруппировать, вынести общий множитель за скобки и привести подобные слагаемые:
4x — 3y + y — 2x = (4x — 2x) + (-3y + y) = (4 — 2)x + (-3 + 1)y = 2x — 2y.
Пример 2. Раскройте скобки и приведите подобные слагаемые:
4(a — 3b) — (a — 2b).
Решение:
4(a — 3b) — (a — 2b) = 4a — 12b — a + 2b = 3a — 10b.
Приведение подобных членов
В предыдущем мы имели много примеров, в которых, при помощи нашего знания о значении коэффициентов, мы более короткий многочлен заменяли более длинным.
Так, трехчлен 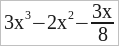
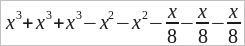
a + a + a + a – b – b – b = 4a – 3b
x – y – y + x – y – y + x = 3x – 4y
Поясним, например, 2-ой пример. Мы видим, что в этом многочлене слагаемое (+x) повторяется три раза. Мы можем, переставив члены многочлена, сделать так, чтобы эти три слагаемых оказались рядом; тогда сумму +x + x + x мы можем заменить одним членом, воспользовавшись коэффициентом +3, т. е. членом 3x. Далее мы получим, после указанной перестановки членов, четыре слагаемых, написанных рядом –y – y – y – y, мы можем, воспользовавшись коэффициентом –4, заменить эти 4 члена одним –4y.
Вот еще несколько примеров:
Рассмотрим далее пример:
a – 2b + 3a – b + a – 3b
Зная значения коэффициентов, имеющихся у некоторых членов этого многочлена, мы могли бы заменить второй член этого многочлена –2b через –b – b, третий член +3a через +a + a + a и последний член –3b через –b – b – b, и тогда мы увидали бы,что во всем многочлене a повторяется слагаемым 5 раз, что можно выразить коэффициентом +5, –b повторяется слагаемым 6 раз, что можно выразить коэффициентом –6 при множителе b, т. е.
a – 2b + 3a – b + a – 3b = 5a – 6b
Также
x + 9x – y – 7y + 11x – 2y + 4x = 25x – 10y
a³ – 3a² + 14a³ – 2a² = 15a³ – 5a²
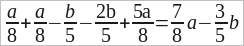
Пусть теперь имеем двучлен
5a – 8a
Зная значение коэффициентов, мы видим, что
5a – 8a = a + a + a + a + a – a – a – a – a – a – a – a – a
Так как известно, что +a и –a взаимно уничтожаются (или +a – a = 0), то предыдущая сумма сведется к –a – a – a или к –3a, т. е.
5a – 8a = –3a
Также
5x – 2x = x + x + x + x + x – x – x = 3x.
Возьмем теперь многочлен
12a – 4b – 3c + 4a + 7b – 2c – 6a – 4b + 5c.
Мы видим, что здесь сначала +a повторяется слагаемым 12 раз, затем 4 раза, а затем –a повторяется слагаемым 6 раз. Так как –6a взаимно уничтожаются c +6a, то остается после этого +a, повторенное слагаемым 10 раз, т. е. получим член +10a.
Также члены –4b + 7b – 4b вместе дадут лишь член –b, а члены –3c – 2c + 5c взаимно уничтожатся. Поэтому
2a – 4b – 3c + 4a + 7b – 2c – 6a – 4b + 5c= 10a – b.
Те упрощения многочленов, какие имели место в ряде предыдущих примеров, называются приведением подобных членов многочлена. Смысл этого преобразования состоит в том, что мы можем в одном многочлене те члены, буквенные множители которых совершенно одинаковы, заменять одним членом.
Эти члены, о которых здесь идет речь, имеющие одинаковых буквенных множителей, называются подобными членами. Так, 3a²b³ и –5a²b³ суть подобные члены и их можно, если они являются членами одного многочлена, заменить одним членом, но члены 3a³b и –5a²b не суть подобные, ибо их буквенные множители не одинаковы: у первого члена есть буквенный множитель a³, а у второго имеется множитель a², но не a³, и эти два члена, если они даже являются членами одного многочлена, нельзя соединить в один член.
Соединение подобных членов многочлена в один член и называется приведением подобных членов многочлена.
Чтобы научиться быстрее выполнять это преобразование, рассмотрим следующие 4 основных примера:
1) 12ab² + 23ab²
2) –7a³b² – 8a³b²
3) 12a²b – 7a²b
4) 6a²b² – 11a²b²
Зная значение входящих сюда коэффициентов, мы найдем результаты:
12ab² + 23ab² = 35ab²
–7a³b² – 8a³b² = –15a³b²
12a²b – 7a²b = 5a²b
6a²b² – 11a²b² = –5a²b²
Рассматривая эти результаты, мы прежде всего видим, что при приведении подобных членов буквенные множители остаются неизменными. Далее в 1-м примере у двух подобных членов были коэффициенты +12 и +23, а у результата получился коэф. +35. Ясно, что пришлось коэффициенты приводимых подобных членов сложить, также точно во 2-м примере были коэффициенты –7 и –8, а в результате коэф. = –15. Здесь также пришлось выполнить сложение (абсолютные величины сложить и приписать общий знак). В 3-м примере были коэффициенты +12 и –7, а у результата получился коэффициент +5, в 4-м из коэффиц. +6 и –11 получился коэффиц. –5. Вспоминая, что при сложении относительных чисел надо абсолютные их величины вычитать арифметически (из большей меньшую) и брать знак того числа, у которого абсолютная величина больше, мы придем к заключению, что и в этих случаях коэффициенты приходится складывать. Дело не меняется, если коэффициенты возьмем дробные. Итак,
чтобы выполнить приведение подобных членов многочлена (другими словами: чтобы все подобные члены одного многочлена соединить в один), надо сложить их коэффициенты, а буквенные множители оставить без изменения.
Конечно, если в многочлене 3 или более подобных членов, то можно выполнять сложение их коэффициентов в любом порядке.
Примеры:
Здесь для удобства подобные члены подчеркнуты одинаковыми знаками.
Примеры:
-
одночлены (2)(x) и (5)(x) – подобны, так как и там, и там буквы одинаковы: икс;
-
одночлены (x^2y) и (-2x^2y) – подобны, так как и там, и там буквы одинаковы: икс в квадрате, умноженный на игрек. То, что перед вторым одночленом стоит знак минус не играет роли, просто у него отрицателен числовой множитель (коэффициент);
-
одночлены (3xy) и (5x)– не подобны, так как в первом одночлене буквенные множители икс и игрек, а во втором – только икс;
-
одночлены (xy3yz) и (y^2 z7x) – подобны. Однако чтоб это увидеть, необходимо привести одночлены к стандартному виду. Тогда первый одночлен будет выглядеть как (3xy^2z), а второй как (7xy^2z) — и их подобие станет очевидно;
-
одночлены (7x^2) и (2x) – не подобны, так как в первом одночлене буквенные множители икс в квадрате (то есть (x·x)) , а во втором – просто один икс.
Как определяются подобные члены не нужно запоминать, лучше просто понять. Почему (2x) и (5x) называют подобными? А вы вдумайтесь: (2x) это тоже самое, что (x+x), а (5x) тоже самое, что (x+x+x+x+x). То есть, (2x) — это «два икса», а (5x) — «пять иксов». И там, и там в основе — одинаковое (подобное): икс. Просто разное «количество» этих самых иксов.
Другое дело, например, (5x) и (3xy). Здесь первый одночлен это по сути «пять иксов», а вот второй — «три икс(·)игреков» ((3xy=xy+xy+xy)). В основе – не одинаковое, не подобное.
Приведение подобных слагаемых
Подобные слагаемые можно складывать и вычитать, заменяя сложные выражения на более простые. Например, выражение (2x+5x) без проблем можно заменить на (7x). Логика такой замены понятна из пояснения выше:

Процесс замены суммы или разности подобных слагаемых одним одночленом называется «приведение подобных слагаемых».
Отметим при этом, что если слагаемые не подобны, то привести их не получится. Например, в сложить (2x^2) и (3x) – нельзя, они же разные!

Поймите, складывать не подобные слагаемые — все равно, что складывать рубли с килограммами: полная бессмыслица получится.
Приведение подобных слагаемых – весьма часто встречающийся шаг в упрощении выражений и алгебраических дробей, а также при решении уравнений и неравенств. Давайте посмотрим конкретный пример применения полученных знаний.
Пример. Решить уравнение (7x^2+3x-7x^2-x=6)
|
(7x^2+3x-7x^2-x=6) |
В левой части уравнения есть подобные слагаемые: (7x^2) и ((-7x^2)), а также (3x) и ((-x)). Перепишем уравнение так, чтоб они стояли рядом. Для этого меняем местами слагаемые одночлены, не забывая сохранять знаки. |
|
|
(7x^2-7x^2+3x-x=6) |
Теперь приводим подобные. (7x^2) и ((-7x^2)) дадут в результате ноль. Действительно, если из (7x^2) вычесть (7x^2) — что получиться? Ноль. Поэтому их можно просто сократить: зачеркнуть. Они не играют роли. А (3x-x) можно записать как (2x). |
|
|
(2x=6) |
Получили простое линейное уравнение. Делим его на (2) и получаем ответ. |
|
|
(x=3) |
Ответ: (3)
Каждый раз переписывать уравнение так, чтоб подобные стояли рядом совсем необязательно, можно приводить их сразу. Здесь это было сделано для наглядности дальнейших преобразований.
Смотрите также:
Раскрытие скобок
Скачать статью
6.4.2. Раскрытие скобок. Приведение подобных слагаемых
1. Раскрытие скобок, перед которыми стоит знак «+» или не стоит никакого знака.
Если перед скобками стоит знак «+» или не стоит никакого знака, то убираем скобки, знак «+» и записываем слагаемые, стоявшие в скобках, без изменений.
Примеры. Раскрыть скобки.
1в) 7x+(-a-2b+5c-k) = 7x-a-2b+5c-k.
2. Раскрытие скобок, перед которыми стоит знак «-».
Если перед скобками стоит знак «-», то убираем скобки, знак «-» и записываем слагаемые, стоявшие в скобках, с противоположными знаками.
Примеры. Раскрыть скобки.
2б) — (-2a+c) — (b-3d) = 2a-c-b+3d;
2в) — (4k-m) — (-a+2b) = -4k+m+a-2b.
3. Слагаемые, имеющие одинаковую буквенную часть, называются подобными слагаемыми. Примеры подобных слагаемых: 5а и -а; 2с и -12с.
Числовой множитель, стоящий перед буквенным множителем, называют коэффициентом. Так, в выражении 5а коэффициент равен 5, а в выражении (-а) коэффициент равен (-1).
Нахождение алгебраической суммы подобных слагаемых называется приведением подобных слагаемых.
Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
Примеры. Привести подобные слагаемые.
3а) 2а-7а+9а-6а = (2-7+9-6)а = -2а;
3б) -4m+6m-3m+4m = (-4+6-3+4) m = 3m;
3в) 5,2с-2,8с-6,4с+9с = (5,2-2,8-6,4+9)с = 5с.
4. В алгебраическом выражении могут быть различного вида подобные слагаемые. В этом случае подобные слагаемые подчеркиваются одинаковыми линиями.
Примеры. Привести подобные слагаемые.
4а) -4а +5с-11с -20а = (-4-20)а+(5-11)с = -24а-6с;
4б) 3,2х +5,6у -8х -3у = (3,2-8)х+(5,6-3)у = -4,8х+2,6у;
4в) 8 m -3k +7 m -2k+12k +13 m = (8+7+13) m+(-3-2+12) k = 28m+7k.
5. Для преобразования алгебраических выражений с помощью раскрытия скобок используют распределительное свойство умножения: чтобы сумму чисел умножить на третье число, можно каждое слагаемое умножить на третье число и сложить результаты.
Примеры. Раскрыть скобки.
5а) 2 (4х-5у) = 2 ∙ 4х+2 ∙ (-5) = 8х-10у;
5б) -3 (4а+7с) = -3 ∙ 4а-3 ∙ 7с = -12а-21с;
5в) -6 (-а+4с) = -6 ∙ (-а) -6 ∙ 4с = 6а-24с.
6. Упростить алгебраическое выражение – это значит раскрыть скобки, выполнить указанные действия, привести подобные слагаемые.
Примеры. Упростить выражение.
6а) (3х+у) -2 (5х-у) = 3х +у -10х +2у = -7х+3у;
6б) 3х(а+1,5) -4ах = 3ах +4,5х -4ах = 4,5х-ах;
6в) -6 (х+у)+3 (2х-у) = -6х -6у +6х -3у = -9у.
7. Примеры для самостоятельного решения. Упростить:
Подобные слагаемые, их приведение, примеры
Приведение подобных слагаемых является одним из наиболее употребимых тождественных преобразований. В этом разделе мы дадим определение термина, разберем, что обозначает словосочетание «приведение подобных слагаемых», рассмотрим основные правила выполнения действий и наиболее распространенные типы задач.
Определение и примеры подобных слагаемых
В большинстве учебных пособий тема подобных слагаемых разбирается после знакомства с буквенными выражениями, когда появляется необходимость проводить с ними различные преобразования.
Подобные слагаемые – это слагаемые, которые имеют одинаковую буквенную часть.
Слагаемые – это, как известно, составные элементы суммы. Это значит, что они могут присутствовать лишь в тех выражениях, которые представляют собой сумму. Буквенная часть – это одна или произведение нескольких букв, которые представляют собой переменные. Слагаемые с буквенной частью – это произведение некоторого числа и буквенной части. Здесь некоторое число также носит название числового коэффициента.
Рассмотрим сумму двух слагаемых 3 · a + 2 · a . В этой сумме слагаемые имеют одну и ту же буквенную часть, которая представлена буквой a . Согласно определению, эти два слагаемых являются подобными. Числа 2 и 3 в данном случае являются числовыми коэффициентами.
Рассмотрим сумму 5 · x · y 3 · z + 12 · x · y 3 · z + 1 . Здесь подобными являются слагаемые 5 · x · y 3 · z и 12 · x · y 3 · z , которые имеют одинаковую буквенную часть x · y 3 · z . Следует обратить внимание на то, что в буквенной части присутствует степень y 3 . Наличие степени не нарушает данное выше определение буквенной части в связи с тем, что y 3 по сути является произведением y · y · y .
Числовые коэффициенты 1 и − 1 в случае подобных слагаемых часто не записываются, но подразумеваются. К примеру, сумма 3 · z 5 + z 5 − z 5 состоит из трех слагаемых 3 · z 5 , z 5 и − z 5 , которые являются подобными. Здесь z 5 – это одинаковая буквенная часть, 3 , 1 и — 1 – коэффициенты.
Если слагаемые в буквенном выражении не имеют буквенной части, то они также являются подобными. Например, сумма 5 + 7 · x − 4 + 2 · x + y представлена 4 подобными слагаемыми, два из которых ( 5 и — 4 ) не имеют буквенной части.
Буквенная часть может быть представлена не только произведением букв, но также и произвольным буквенным выражением. Например:
3 · 5 · a — 2 · 5 · a + 12 · 5 · a .
Здесь общей буквенной частью подобных слагаемых является выражение 5 · a .
По аналогии можно выделить подобные слагаемые в выражении 4 · ( x 2 + x − 1 / x ) − 0 , 5 · ( x 2 + x − 1 / x ) − 1 . Это будут слагаемые с одинаковой буквенной частью ( x 2 + x − 1 / x ) .
Обобщим изложенные выше утверждения и дадим еще одно определение подобных слагаемых.
Подобные слагаемые – это слагаемые в буквенном выражении, которые имеют одинаковую буквенную часть, а также слагаемые, которые не имеют буквенной части, если под буквенной частью понимать любое буквенное выражение.
Числовые коэффициенты подобных слагаемых могут быть равны, тогда мы говорим о том, что подобные слагаемые одинаковые. Если же числовые коэффициенты различаются, то подобные слагаемые будут разными.
Возьмем для примера выражение 2 · x · y + 3 · y · x и рассмотрим такой нюанс: являются ли слагаемые 2 · x · y и 3 · y · x подобными. В задачах этот вопрос может иметь следующую формулировку: одинаково ли буквенное выражение части x · y и y · x указанных слагаемых? Буквенные множители в приведенном примере имеют различный порядок, что в свете данного выше определения не делает их подобными.
Однако, если использовать переместительное свойство умножения, то можно изменить порядок множителей, не влияя на результат умножения. Это позволяет нам переписать выражение 2 · x · y + 3 · y · x можно переписать в виде 2 · x · y + 3 · x · y . Тогда слагаемые будут подобны.
К слову, в некоторых источниках при нестрогом отношении к вопросу, слагаемые из примера могут называться подобными. Но лучше не допускать таких неточностей в трактовках.
Приведение подобных слагаемых, правило, примеры
Под преобразованием выражений, которые содержат подобные слагаемые, подразумевается проведение сложения этих слагаемых. Проводится это действие обычно в три этапа:
- перестановка слагаемых таким образом, чтобы подобные слагаемые оказались рядом;
- вынесение за скобки буквенной части;
- вычисление значения числового выражения, которое осталось в скобках.
Приведем пример таких вычислений.
Возьмем выражение 3 · x · y + 1 + 5 · x · y . Выделим подобные слагаемые и переставим их друг к другу: 3 · x · y + 1 + 5 · x · y = 3 · x · y + 5 · x · y + 1 .
Теперь вынесем за скобки буквенную часть: x · y · ( 3 + 5 ) + 1 .
Нам осталось вычислить значение выражения, которое записано в скобках: x · y · ( 3 + 5 ) + 1 = x · y · 8 + 1 .
Обычно числовой коэффициент записывается перед буквенной частью: x · y · 8 + 1 = 8 · x · y + 1 .
Описанные три шага для экономии времени записывают в виде правила приведения подобных слагаемых. Согласно правило для того, чтобы привести подобные слагаемые, необходимо сложить их коэффициенты, а затем умножить полученный результат на буквенную часть при ее наличии.
Запишем более короткий вариант решения выражения, рассмотренного выше. В выражении 3 · x · y + 1 + 5 · x · y коэффициентами подобных слагаемых 3 · x · y и 5 · x · y являются числа 3 и 5 . Сумма коэффициентов равна 8 . Умножим ее на буквенную часть и получим: 3 · x · y + 1 + 5 · x · y = 8 · x · y + 1 .
Приведите подобные слагаемые: 0 , 5 · x + 1 2 + 3 , 5 · x − 1 4 .
Решение
Начнем с приведения подобных слагаемых 0 , 5 · x и 3 , 5 · x . Используя правило, сложим их коэффициенты 0 , 5 + 3 , 5 = 4 . Умножим буквенную часть на полученный результат 4 · x .
Теперь займемся приведением подобных слагаемых без буквенной части: 1 2 + ( — 1 4 ) = 1 2 — 1 4 = 1 4 . Вспомним правило сложения чисел с разными знаками и выполним вычитание обыкновенных дробей. Получим: 1 2 + ( — 1 4 ) = 1 2 — 1 4 = 1 4
Итог: 0 , 5 · x + 1 2 + 3 , 5 · x − 1 4 = 4 · x + 1 4 .
Приведем краткую запись решения: 0 , 5 · x + 1 2 + 3 , 5 · x − 1 4 = ( 0 , 5 · x + 3 , 5 · x ) + ( 1 2 − 1 4 ) = 4 · x + 1 4 .
Ответ: 0 , 5 · x + 1 2 + 3 , 5 · x − 1 4 = 4 · x + 1 4 .
Особо хочется отметить тот факт, что приведение подобных слагаемых базируется на распределительном свойстве умножения относительно сложения, которое можно выразить равенством a · ( b + c ) = a · b + a · c . Когда мы выполняем приведение подобных слагаемых, мы используем это равенство справа налево, т.е. в виде a · b + a · c = a · ( b + c ) .
Подобные слагаемые
Свойства сложения и умножения
В буквенных выражениях числа могут быть обозначены буквами. Поэтому для всех буквенных выражений верны следующие равенства, выражающие свойства сложения и свойства умножения:
| Свойства сложения | Свойства умножения |
|---|---|
| a + b = b + a (a + b) + c = a + (b + c) a + 0 = a a + (-a) = 0 a — b = a + (-b) |
ab = ba (ab)c = a(bc) a(b + c) = ab + ac a = 1 · a —a = -1 · a a · 0 = 0 |
С помощью этих свойств можно упрощать буквенные выражения. Например:
Слагаемые 5a, 12a и -7a отличаются только числовыми множителями, такие слагаемые называются подобными.
Подобные слагаемые
Подобные слагаемые — это слагаемые, отличающиеся только числовыми множителями и имеющие одинаковую буквенную часть. Пользуясь свойствами сложения и умножения, можно упрощать выражения, содержащие подобные слагаемые. Например, упростим выражение:
Такое упрощение выражения называется приведением подобных слагаемых. В простых примерах промежуточные вычисления можно опустить:
Приведение подобных слагаемых
Приведение подобных слагаемых — это упрощение выражения, содержащего подобные слагаемые, путём их сложения.
Пример 1. Приведите подобные слагаемые:
Решение: Сначала надо найти в выражении подобные слагаемые:
| 4x | — | 3y | + | y | — | 2x | , |
теперь можно их сгруппировать, вынести общий множитель за скобки и привести подобные слагаемые:
Пример 2. Раскройте скобки и приведите подобные слагаемые:
источники:
http://zaochnik.com/spravochnik/matematika/vyrazhenija/podobnye-slagaemye/
http://izamorfix.ru/matematika/arifmetika/podobnye_slagaemye.html
Сегодня на уроке мы узнаем, какие слагаемые
называют подобными, а также научимся приводить подобные слагаемые или, проще
говоря, упрощать выражения.
Для изучения нового материала нам понадобятся
понятие «коэффициента» и знание распределительного свойства умножения.
Вспомним их.
Коэффициентом называют числовой
множитель, который записан перед буквенным (одним или несколькими) множителем.
Распределительное свойство умножения
справедливо для любых чисел a,
b и c.
Оно позволяет, как раскрывать скобки, так и
выносить общий множитель за скобки.
Часто при работе с выражениями сначала их
обычно упрощают, т.е. преобразуют в более компактную и удобную для вычислений
форму.
Например
Найти значение выражения 5х + 2х – 3х + 7х при х = 3.
Конечно, можно просто подставить вместо х указанное
значение и посчитать сумму полученных произведений.
Но такой процесс вычислений займёт немало
времени. Вычисления значительно упростятся, если обратить внимание, на то, что
все слагаемые имеют один и тот же буквенный множитель х. И вот тут к нам на помощь приходит распределительное
свойство умножения. Мы знаем, что на основании распределительного
свойства можно выносить общий множитель за скобки. Вынесем в нашем
выражении общий буквенный множитель х за скобки.
Смотрите, как мы себе упростили вычисления.
Такие преобразования можно выполнять только в тех случаях, когда слагаемые
имеют одинаковую буквенную часть.
Такие слагаемые называют подобными,
а сами преобразования называют приведением подобных слагаемых.
Определение
Слагаемые, имеющие одинаковую буквенную часть,
называют подобными слагаемыми.
Замену суммы подобных слагаемых одним
слагаемым называют приведением подобных слагаемых.
Подобные слагаемые могут отличаться только
коэффициентами. Кроме того, подобными считают и равные слагаемые, а также
числа.
Заметим, что слагаемые, у которых равны
коэффициенты, а буквенные множители различны, подобными не являются,
хотя и к ним иногда полезно применять распределительное свойство умножения.
Например
Ответим на вопрос: зачем же нужно
приводить подобные слагаемые?
Ответ на этот вопрос прост. Приводят
подобные слагаемые для того, чтобы сделать суммы более короткими, т.е. преобразовывают
их в суммы с меньшим числом слагаемых.
Посмотрите, в нашей начальной сумме было 4 слагаемых, а мы её преобразовали в выражение,
состоящее из двух множителей. С более короткими суммами легче выполнять
вычисления.
Запишем правило, по которому приводят
подобные слагаемые:
Для того чтобы привести подобные
слагаемые, надо:
1) сложить коэффициенты подобных
слагаемых;
2) результат умножить на общую буквенную
часть.
Задание
Упростите выражения.
Итоги
Слагаемые, имеющие одинаковую буквенную часть,
называют подобными слагаемыми.
Замену суммы подобных слагаемых одним
слагаемым называют приведением подобных слагаемых.
Для того чтобы привести подобные слагаемые,
надо:
1) сложить коэффициенты подобных слагаемых;
2) результат умножить на общую буквенную
часть.